Please help me! Find the value of X&Y for which ABCD must be a parallelogram!

Answers
Answer:
x = 8y = 6Step-by-step explanation:
You want the values of x and y that make the quadrilateral a parallelogram, given the halves of one diagonal are marked (3x-14) and (x+2), and the halves of the other diagonal are marked (4y-7) and (y+11).
ParallelogramThe diagonals of a parallelogram bisect each other. This means the marked segments on each diagonal are congruent.
x-value(3x -14) = (x +2)
2x = 16 . . . . . . . . . add 14-x
x = 8 . . . . . . . . divide by 2
y-value(4y -7) = (y +11)
3y = 18 . . . . . . . . . add 7-y
y = 6 . . . . . . . . divide by 3
The values of x and y are 8 and 6, respectively.
Related Questions
What is the value of v?

Answers
░░░░░░░░░░░▄▀▄▀▀▀▀▄▀▄░░░░░░░░░░░░░░░░░░
░░░░░░░░░░░█░░░░░░░░▀▄░░░░░░▄░░░░░░░░░░
░░░░░░░░░░█░░▀░░▀░░░░░▀▄▄░░█░█░░░░░░░░░
░░░░░░░░░░█░▄░█▀░▄░░░░░░░▀▀░░█░░░░░░░░░
░░░░░░░░░░█░░▀▀▀▀░░░░░░░░░░░░█░░░░░░░░░
░░░░░░░░░░█░░░░░░░░░░░░░░░░░░█░░░░░░░░░
░░░░░░░░░░█░░░░░░░░░░░░░░░░░░█░░░░░░░░░
░░░░░░░░░░░█░░▄▄░░▄▄▄▄░░▄▄░░█░░░░░░░░░░
░░░░░░░░░░░█░▄▀█░▄▀░░█░▄▀█░▄▀░░░░░░░░░░
░░░░░░░░░░░░▀░░░▀░░░░░▀░░░▀░░░░░░░░░░░░
the least-squares solution of a x = b is the vector in the column space of a closest to b. true or false?
Answers
the least-squares solution of a x = b is the vector in the column space of a closest to b. then the statement is true
Aleast- squares solution of is a vector such that for all in .
The statement is true because the general least-squares problem attempts to find an that maximizes .
The above statement is actually the one that validates the least-square solution statement.
Hence , the least-squares solution of a x = b is the vector in the column space of a closest to b .then the statement is true
learn more about of squares here
https://brainly.com/question/23305357
#SPJ4
You would like to study all of the numbers that are at a distance 10 or less from a number -20. Write this using absolute value notation and use the variable x
Answers
Answer:
Step-by-step explanation:
dad hates me sorry bye
Checking for approximate normality in the population is essential for constructing a valid confidence interval, particularly when dealing with small sample sizes. This ensures the accuracy and reliability of the interval in estimating the true population parameter.
It's important to check whether the population is approximately normal before constructing a confidence interval because the accuracy and validity of the interval depend on the underlying distribution of the population. Here's a step-by-step explanation:
1. A confidence interval is a range of values within which the true population parameter (e.g., mean or proportion) is likely to fall, with a certain level of confidence (e.g., 95% or 99%).
2. The process of constructing a confidence interval relies on the Central Limit Theorem, which states that, for large sample sizes, the sampling distribution of the sample mean will be approximately normal, regardless of the population distribution.
3. However, for small sample sizes, the distribution of the population needs to be approximately normal in order to obtain an accurate confidence interval. This is because the normality assumption is crucial for the proper interpretation of the interval.
4. If the population is not approximately normal, the confidence interval may not provide a reliable estimate of the true population parameter, leading to incorrect conclusions and potentially invalid results.
Learn more about Central limit theorem here: brainly.com/question/18403552
#SPJ11
How do you find the hypotenuse of a 45-45-90 triangle if you know the length of the legs?
Answers
The length of the hypotenuse of a 45-45-90 triangle is √2x units.
To find the hypotenuse of a 45-45-90 triangle, we can use the Pythagorean theorem, which states that in a right triangle, the sum of the squares of the two shorter sides (legs) is equal to the square of the longest side (hypotenuse).
Let's denote the length of each leg of the triangle as "x". Since the triangle is isosceles, both legs are of equal length. Therefore, we can write:
Leg 1 = Leg 2 = x
To find the length of the hypotenuse (which we'll call "h"), we can use the Pythagorean theorem as follows:
x² + x² = h²
Simplifying this equation, we get:
2x² = h²
To solve for h, we need to take the square root of both sides of the equation:
√(2x²) = √(h²)
√2 * x = h
To know more about triangle here
https://brainly.com/question/8587906
#SPJ4
Is ΔWXZ ≅ ΔYZX? Why or why not? Yes, they are congruent by SAS. Yes, they are both right triangles. No, the triangles share side XZ. No, there is only one set of congruent sides.
Answers
Answer:
Yes, they are congruent by SAS.
Step-by-step explanation:
Answer:
Yeah your answer would be A. Yes, they are congruent by SAS!
hope this helps :D
Step-by-step explanation:
Each period, demand for apples is normally distributed with a mean of 290 and standard deviation of 70. Answer is complete but not entirely correct. Round your answer to two decimal places. What is the standard deviation of demand over 2 periods?
Answers
Given that demand for apples each period follows a normal distribution with a mean of 290 and a standard deviation of 70.
The standard deviation of demand over two periods is the square root of the sum of variances of each period. Since the variance is the square of the standard deviation, the formula for variance over two periods is$$
\begin{aligned}
\operatorname{Var}(2T) &= \operatorname{Var}(T) + \operatorname{Var}(T) \\
&= 2 \operatorname{Var}(T)
\end{aligned}
$$where T is the demand for apples in one period. Here, the standard deviation of demand for apples in one period is σ = 70. Therefore, the standard deviation of demand over two periods is given by$$
\begin{aligned}
\operatorname{SD}(2T) &= \sqrt{2\operatorname{Var}(T)} \\
&= \sqrt{2}\sigma \\
&= \sqrt{2} \times 70 \\
&= \boxed{98.99} \approx 99 \text{ (rounded to two decimal places)}
\end{aligned}
$$Therefore, the standard deviation of demand over two periods is approximately 99.
to know more about distribution visit :
https://brainly.com/question/29664127
#SPJ11
The correct answer of the given question that standard deviation of demand for two periods is 99.00.
Given data:
The mean of the demand for apples is 290, and the standard deviation is 70.
The formula for standard deviation of a sample is:
SD = sqrt[(sum of (Xi - Xbar)^2) / (n - 1)]
where Xi is the individual data value, Xbar is the mean of the sample, and n is the sample size.
Since we don't have the data for the demand in each period, we cannot calculate the standard deviation of the demand for two periods directly.
However, since the standard deviation is a measure of how much the individual data points deviate from the mean, we can use the following formula to calculate the standard deviation of the demand for two periods:
SD2 = sqrt(2) * SD
where SD is the standard deviation of demand for one period.
So,SD2 = sqrt(2) * 70 = 99.00 (rounded to two decimal places)
Hence, the standard deviation of demand for two periods is 99.00.
To know more about standard deviation, visit:
https://brainly.com/question/29115611
#SPJ11
Find all solutions of the equation in the interval [0, 2π]. cos 2x/3 = 0
Write your answer in radians in terms of π. If there is more than one solution, separate them with commas.
Answers
The solution to the equation cos(2x/3) = 0 in the interval [0, 2π] is x = (3π/4).
The inverse cosine of 0 is π/2 radians or 90 degrees, but we need to consider all possible solutions within the given interval [0, 2π]. Since the cosine function has a period of 2π, we can find all the solutions by adding integer multiples of the period to the initial solution.
Let's calculate the initial solution:
cos(2x/3) = 0
Taking the inverse cosine of both sides:
arccos(cos(2x/3)) = arccos(0)
Simplifying the left side using the fact that arccos and cos are inverse functions:
2x/3 = π/2
To isolate x, we'll multiply both sides of the equation by 3/2:
(2x/3) * (3/2) = (π/2) * (3/2)
x = (3π/4)
So, one solution in the interval [0, 2π] is x = 3π/4.
Now, let's find the other solutions by adding integer multiples of the period. Since the period is 2π, we can add 2πk to the initial solution, where k is an integer.
x = (3π/4) + 2πk
We need to ensure that all the solutions are within the given interval [0, 2π]. Let's substitute k = 0, 1, 2, and so on, until we find the solutions within the interval:
For k = 0:
x = (3π/4) + 2π(0) = (3π/4)
For k = 1:
x = (3π/4) + 2π(1) = (3π/4) + (2π) = (11π/4)
The value (11π/4) is outside the given interval [0, 2π], so we stop here.
To know more about equation here
https://brainly.com/question/21835898
#SPJ4
This problem please

Answers
surface areas:
1. 94 ft
2. 96 cm
volumes:
1. 60 ft
2. 42 cm
John is 20 years old than Steve. In 10 years, Steve's age will be half that of John's. What is the Steve age??
Answers
Answer:Steve age will be 15 y.o
Step-by-step explanation:
A sample of 34 observations is selected from a normal population. The sample mean is 28, and the population standard deviation is 4. Conduct the following test of hypothesis using the 0.05 significance level.
H0: μ ≤ 26
H1: μ > 26
a.Is this a one- or two-tailed test?
One-tailed test
Two-tailed test
b.What is the decision rule?
Reject H0 when z > 1.645
Reject H0 when z ≤ 1.645
c.What is the value of the test statistic? (Round your answer to 2 decimal places.)
d.What is your decision regarding H0?
Reject H0
Fail to reject H0
e-1) What is the p-value? (Round your answer to 4 decimal places.)
e-2)Interpret the p-value? (Round your final answer to 2 decimal places.)
Answers
a. The alternative hypothesis (H1) specifies that is greater than 26, indicating a directed alternative, this is a one-tailed test.
b. The alternative hypothesis is one-sided and argues that > 26, hence the critical value is 1.645.
c. The value of the test statistic (z-score) is z ≈ 3.82.
d. We reject the null hypothesis (H0) because the test statistic (z = 3.82) is higher than the crucial value (1.645).
In this case, the p-value is the probability of observing a sample mean of 28 or greater, assuming the population mean is 26.
a. This is a one-tailed test because the alternative hypothesis (H1) states that μ is greater than 26, indicating a directional alternative.
b. The decision rule for a one-tailed test at a significance level of 0.05 is to reject the null hypothesis (H0) if the test statistic is greater than the critical value. In this case, the critical value is 1.645 because the alternative hypothesis is one-sided and states that μ > 26.
c. The value of the test statistic (z-score) can be calculated using the formula:
z = (x - μ) / (σ / √n)
where x is the sample mean, μ is the population mean, σ is the population standard deviation, and n is the sample size.
In this case:
x = 28
μ = 26
σ = 4
n = 34
Substituting the values into the formula:
z = (28 - 26) / (4 / √34) ≈ 3.82
d. Since the test statistic (z = 3.82) is greater than the critical value (1.645), we reject the null hypothesis (H0).
e-1. To calculate the p-value, we need to find the area under the standard normal distribution curve to the right of the test statistic (z = 3.82). We can use a standard normal distribution table or a calculator to find this area.
The p-value is the probability of observing a test statistic as extreme as the one calculated (or more extreme) under the null hypothesis.
e-2. Interpreting the p-value: The p-value represents the probability of obtaining a sample mean as extreme as the one observed (or more extreme) if the null hypothesis is true.
learn more about hypothesis from givn link
https://brainly.com/question/606806
#SPJ11
let f be the function given by . what are all values of c that satisfy the conclusion of the mean value theorem of differential calculus on the closed interval [0,3]?
Answers
The only value of c that satisfies the conclusion of the Mean Value Theorem on the closed interval [0,3] is c = 2.
The Mean Value Theorem states that if a function f is continuous on a closed interval [a, b], then there exists some c in the interval such that
f'(c) = (f(b) - f(a)) / (b - a).
In the case of f(x) = x(x-3) , on the closed interval [0,3], we can solve for c using the equation above.
We begin by calculating f'(c), which is equal to 2c - 3. Then, we set the equation equal to (f(3) - f(0)) / (3 - 0), which is equal to -3 / 3.
Substituting this into our equation for f'(c), we get 2c - 3 = -1, which simplifies to c = 2.
Therefore, the only value of c that satisfies the conclusion of the Mean Value Theorem on the closed interval [0,3] is c = 2.
Learn more about mean value theorem here:
https://brainly.com/question/29107557
#SPJ4
is 3/8 rational or irrational
Answers
Answer:
Step-by-step explanation:
rational because 3/4 is rational.
As regards if the fraction 3/8 is a rational or irrational number, the correct answer is that it is a rational number.
Why is 3/8 a rational number?Rational numbers are numbers and fractions that are finite in nature. This means that they do not keep on going with non zero digits.
When converted to a decimal, the number 3/8 is:
= 3/8
= 3 ÷ 8
= 0.375
3/8 does not repeat so it is a rational number.
Find out more on rational numbers at https://brainly.com/question/12088221.
#SPJ2
MULTIPLE CHOICE QUESTION
In the equation 8x = 6x - 12, what is the first step to solving this equation?
Subtract 6x from both sides
add 8x + 6x
Subtract 8x from both sides
Add 12 to both sides
Answers
Answer:
add 12 to both sides
Step-by-step explanation:
Answer:
subtract both side by 6x
define the random variables x and x in words. x is the amount of time an individual waits at the courthouse to be called for service. x is the mean wait time for a sample of individuals. x is the number of individuals at the courthouse to be called for service. x is the average number of individuals at the courthouse
Answers
X is the amount of time individual waits at the courthouse to be called for service. X-bar is the mean wait time for a sample of individuals.
What is a random variable?
A random variable is a mathematical representation of a quantity or object that is affected by random events. It is a mapping or function from possible outcomes in a sample space to a measurable space, which is frequently real numbers.
Assume a committee is investigating whether there is excessive time waste in our judicial system. It is curious about the average amount of time people spend at the courthouse waiting to be called for jury duty. The committee polled 81 people who had recently served as jurors at random. The average wait time for the sample was 4 hours, with a standard deviation of 1.2 hours. In words, define the random variables X and.
X is the amount of time individual waits at the courthouse to be called for service. is the mean wait time for a sample of individuals.
The random variable X is the amount of time for which each of the prospective jurors waits at the courthouse before being called for service. is the mean wait time for the given sample of individuals. In the case given,
Hence, X is the amount of time individual waits at the courthouse to be called for service. X-bar is the mean wait time for a sample of individuals.
To learn more about random variables, visit:
https://brainly.com/question/17217746
#SPJ4
Suppose that all college freshmen have to take a statistics proficiency during the week of registration. Scores are normally distributed with a mean of 75 and a standard deviation of 8.
A Fortune 500 company announces that freshmen whose scores are between 85 and 95 are eligible to its special summer internship program. What is the probability that a freshman would be eligible for this program?
Answer format: Number: Round to: 2 decimal places.
Answers
The probability that a freshman would be eligible for the internship program is 0.0994, which rounded to two decimal places is 0.09.
The given problem involves a normally distributed set of scores with a mean of 75 and a standard deviation of 8. To calculate the probability of a freshman being eligible for the internship program, we need to find the area under the normal curve between the scores of 85 and 95.
First, we need to standardize the scores using the z-score formula: z = (x - μ) / σ, where x is the score, μ is the mean, and σ is the standard deviation. For the score of 85, the z-score would be (85 - 75) / 8 = 1.25, and for the score of 95, the z-score would be (95 - 75) / 8 = 2.5.
Next, we use a standard normal distribution table or a calculator to find the cumulative probability associated with these z-scores. The cumulative probability for a z-score of 1.25 is 0.8944, and for a z-score of 2.5, it is 0.9938.
To find the probability between these two z-scores, we subtract the lower cumulative probability from the higher cumulative probability: 0.9938 - 0.8944 = 0.0994.
Learn more about Probability
brainly.com/question/14210034
#SPJ11
A medical helicopter flies about 150 miles per hour. Use the map and the Pythagorean Theorem to determine approximately how long it will take the helicopter to reach the hospital from the crash site.
Answers
Assuming the crash site is (3, 4) and the hospital is (7, 8), the distance between the two points is approximately 5.6 miles.
What is miles?Miles is a unit of distance measurement, equal to 5,280 feet, or 1,760 yards. Miles are often used to measure the distance between two points, such as the distance between two cities. Miles are also used to measure the distance traveled, such as the number of miles a car has driven.
Using the Pythagorean Theorem, the distance between the crash site and the hospital can be determined. Assuming the crash site is (3, 4) and the hospital is (7, 8), the distance between the two points is approximately 5.6 miles.
To calculate the time it will take the medical helicopter to reach the hospital, divide the distance (5.6 miles) by the speed (150 miles per hour). This gives a total time of approximately 37.3 minutes.
It is important to remember that this is an approximation, as wind, visibility, and other factors can affect the helicopter's speed. Additionally, the helicopter may need to make adjustments to its course due to obstacles or other factors. As such, the actual time it takes the helicopter to reach the hospital may be longer or shorter than this estimate.
To know more about miles click-
https://brainly.com/question/25631156
#SPJ1
The net of a right rectangular prism is shown.
What is the surface area of the net?

Answers
The surface area of the net is 45 square inches.
Describe Rectangular Prism.A rectangular prism is a three-dimensional geometric shape that is composed of six rectangular faces, eight vertices, and 12 edges. It is also known as a rectangular parallelepiped or simply a rectangular box. A rectangular prism is different from a cube because its faces are rectangles of different dimensions.
A rectangular prism has several properties that make it useful in mathematics and engineering. Its faces are all rectangles, which means that it has uniform symmetry along two of its axes. It is also a prism, which means that its faces are parallel and congruent, and its lateral faces are all parallelograms.
The volume of a rectangular prism can be calculated by multiplying the length, width, and height of the prism. For example, if a rectangular prism has a length of 4 units, a width of 3 units, and a height of 2 units, its volume would be 4 x 3 x 2 = 24 cubic units. The surface area of a rectangular prism can be calculated by adding up the areas of all of its faces.
Rectangular prisms are used in many real-world applications, such as in architecture, engineering, and manufacturing. They can be used as building blocks for structures and machines, as well as in the design of containers and packaging. Rectangular prisms also have applications in mathematics and computer science, where they are used to model and analyze a variety of problems, such as optimization, data compression, and algorithms.
To find the surface area of the net, we need to find the area of each of the six faces and add them together.
Face 1: 2 in x 2 in = \(4 in^2\)
Face 2: 2 in x 5 in =\(10 in^2\)
Face 3: 3 in x 5 in = \(15 in^2\)
Face 4: 3 in x 2 in =\(6 in^2\)
Face 5: 2 in x 2 in = \(4 in^2\)
Face 6: 2 in x 3 in = \(6 in^2\)
Adding these up, we get:
4 + 10 + 15 + 6 + 4 + 6 = 45
Therefore, the surface area of the net is 45 square inches.
To know more about the area visit:
brainly.com/question/12187609
#SPJ1
Do
this mathematics operations using the rules of precision
(9.11)+(6.232)
(7.4023)x(19)
(9.162)-(2.39)
(0.00482)x(213)
(8.73)/(5.198)
(7644)/(0.13)
Answers
Answer:
Step-by-step explanation:
Sure! I'll perform the mathematical operations using the given numbers and apply the rules of precision. Please find the results below:
(9.11) + (6.232)
The sum of 9.11 and 6.232 is 15.342.
(7.4023) x (19)
The product of 7.4023 and 19 is 140.844.
(9.162) - (2.39)
The difference between 9.162 and 2.39 is 6.772.
(0.00482) x (213)
The product of 0.00482 and 213 is 1.02786.
(8.73) / (5.198)
The division of 8.73 by 5.198 is 1.67920734.
(7644) / (0.13)
The division of 7644 by 0.13 is 58,800.
Please note that the results are rounded to the appropriate number of decimal places based on the precision rules.
what is the average rate of change of the function g(t) over the interval from t = a to t = b?
Answers
Average rate of change gives us the slope of the secant line that connects the two points on the graph of g(t) corresponding to t = a and t = b. This can help us understand how quickly the function is changing over the interval and can be useful in many applications.
How to find the average rate of change of a function g(t) over the interval from t = a to t = b?We need to use the formula:
average rate of change = (g(b) - g(a))/(b - a)
Here, g(b) represents the value of the function at t = b and g(a) represents the value of the function at t = a.
We can use this formula to calculate the average rate of change of g(t) over the given interval. Just substitute the values of g(a), g(b), a, and b into the formula and simplify the expression to get the answer.
Learn more about average rate of change.
brainly.com/question/28744270
#SPJ11
The function f(x)=√x is translated left 5 units and up 3 units to create the function g(x).
What is the domain of g(x)?
{x|x2-5}
{x|x2-3}
{x|x ≥ 3}
{x|x25}
Answers
The calculated domain the function g(x) g(x) is {x | x ≥ -5}.
Calculating the domain of the function g(x)?The function g(x) is obtained by translating the function f(x) left 5 units and up 3 units.
So the equation for g(x) is:
g(x) = √(x + 5) + 3
The domain of g(x) is the set of all values of x for which the expression under the square root is non-negative, since we can't take the square root of a negative number.
So we need to solve the inequality:
x + 5 ≥ 0
Subtracting 5 from both sides, we get:
x ≥ -5
Therefore, the domain of g(x) is {x | x ≥ -5}.
Read more about domain at
https://brainly.com/question/2264373
#SPJ1
michael is 3 33 times as old as brandon. 18 1818 years ago, michael was 9 99 times as old as brandon. how old is brandon now?
Answers
Brandon is currently 6 81 years old.
Let M be Michael's age and B be Brandon's age.
We are given that Michael is 3 33 times as old as Brandon. This means that M = 3 33 × B
We are also given that 18 1818 years ago, Michael was 9 99 times as old as Brandon. This means that M - 18 1818 = 9 99 × (B - 18 1818).
We can combine these two equations to solve for Brandon's current age:
3 33 × B = (9 99 × B) + 18 1818
2 66 × B = 18 1818
B = 18 1818 / 2 66 = 6 81.
Therefore, Brandon is currently 6 81 years old.
Learn more about equations here:
https://brainly.com/question/10413253
#SPJ4
The multiplicity of a root r of the characteristic equation of A is called the algebraic multiplicity of r as an eigenvalue of A. T/F
Answers
True. The multiplicity of a root r of the characteristic equation of matrix A is indeed called the algebraic multiplicity of r as an eigenvalue of A.
The characteristic equation of a square matrix A is obtained by subtracting λI (where λ is an eigenvalue and I is the identity matrix) from A and taking its determinant. The roots of this equation are the eigenvalues of matrix A.
The algebraic multiplicity of an eigenvalue r refers to the number of times r appears as a root of the characteristic equation. In other words, it represents the multiplicity of r as a solution of the equation.
The algebraic multiplicity provides information about the behavior of the eigenvalue r within the matrix A. If the algebraic multiplicity of r is greater than 1, it means that r is a repeated eigenvalue and there exist multiple linearly independent eigenvectors associated with it. On the other hand, if the algebraic multiplicity is 1, r is a simple eigenvalue, indicating that there is only one linearly independent eigenvector corresponding to r.
Learn more about square matrix here:
https://brainly.com/question/27927569
#SPJ11
1-Describe the error in the way the calculation of the slope of the two points is set up and/or solved. Please be specific. Do not just state what the slope should be. Describe the error.
2- Use the same two points from the error analysis question above and show how to calculate the slope correctly. Then, use the correct slope and one of the points to write the equation in point-slope form of the line. Show all work!
Answers
Answer:
Please check explanations for answer
Step-by-step explanation:
Let’s have two points (5,10) and (15,20)
1. Let’s find the slope of these two points
Mathematically, the slope can be calculated using the formula;
m = (y2-y1)/(x1-x2)
So m = (20-10)/(5-15) = 10/-10 = -1
The error here is the formula used in calculating the slope
The formula should be;
m = (y2-y1)/(x2-x1) and not x1-x2
2. To calculate the slope correctly, we have;
m = (y2-y1)/(x2-x1)
So the slope will be;
m = (20-10)/(15-5) = 10/10 = 1
In the point slope form, the equation can be represented as;
y-y1 = m(x-x1)
Let’s use the point (5,10)
y- 10 = 1(x-5)
The above is the point slope form
using one of the points and the correct slope of the line
HELP!
Follow this link to view Jamie’s work. Critique Jamie’s work by explaining the reasonableness of the scenario and the accuracy of the two parts of the graph he described . For any portion of Jamie’s response in which he has made an error, provide and explain an alternative response.
To enhance Jamie’s explanation, describe both sections of the piecewise function using linear equations. Include any limits to the domain.
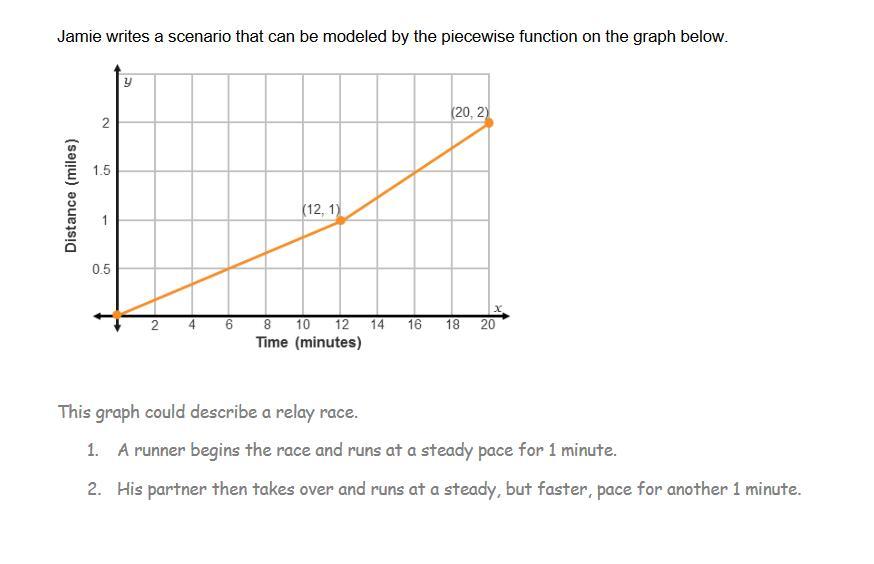
Answers
The given graph is an illustration of a piecewise linear equation.
Jamie correctly described what the graph could be used for (a relay race)
Jamie wrongly described the axes of the graph, in both sections
The piece-wise function is: \(y=\left \{ {{\frac{1}{12}x, 0 < = x < 12} \atop {\frac{1}{8}x+\frac{1}2},12 < x < =20}} \right.\)
See the attachment for the graph and Jamie's work
From the graph, we have:
Time (minutes) = x
Distance (miles) = y
(a) When the runner begins the race
From the graph, we have:
x=[0,12]
y=[0,1]
This means that the runner runs a distance of 1 mile in 12 minutes
So; Jamie's description here is wrong because he misrepresented the axes.
The equation of this part is calculated as follows:
Start by calculating the slope (m)
\(m=\frac{y_2-y_1}{x_2-x_1}\\\\m=\frac{1-0}{12-0}=\frac{1}{12}\)
The equation is then calculated using:
\(y=m(x-x_1)+y_1\\\\y=\frac{1}{12}(x-0)+0\\\\y=\frac{1}{12}x\)
(b) When his partner takes over
From the graph, we have:
x=(12,20]
y=(1,2]
This means that his partner runs a distance of 1 mile in 8 minutes
So; Jamie's description here is also wrong because he misrepresented the axes, again.
The equation of this part is calculated as follows:
Start by calculating the slope (m)
\(m=\frac{y_2-y_1}{x_2-x_1}=\frac{2-1}{20-12}=\frac{1}{18}\\\\y=\frac{1}{8}(x-12}+1\\\\y=\frac{1}{8}x-\frac{1}{2}\)
Hence, the piece-wise function can be represented as:
The piece-wise function is: \(y=\left \{ {{\frac{1}{12}x, 0 < = x < 12} \atop {\frac{1}{8}x+\frac{1}2},12 < x < =20}} \right.\)
Read more about piece-wise equations at:
https://brainly.com/question/16984860
#SPJ1
One of the team members convinced you to use Logistic Regression instead of Classification Tree. What argument did the team member use to change your mind
Answers
The argument used by the team member was that a single line is used to differentiate the space into two. This is will make the presentation more attractive. Even if there are higher-dimensional data the lines will generalize into planes and hyperplanes. So according to the team member, it would be better to use Logistic Regression.
When we use the classification tree presentation the data will be mixed up and will clash against each other. So using the Logistic Regression will be better as this divides the data set into two separate parts. So, if the data are not linearly separable then only we should use the Classification Method.
1. Learn more about Logistic Regression from here:
https://brainly.com/question/21344316
2. Learn more about Classification Tree from here:
https://brainly.com/question/16170403
#SPJ4
The cost of making x items is C(x)=15+2x. The cost p per item and the number made x are related by the equation p+x=25. Profit is then represented by px-C(x) [revenue minus cost]. a) Find profit as a function of x b) Find x that makes profit as large as possible c) Find p that makes profit maximum.
Answers
We are given the cost function C(x) = 15 + 2x and the relationship between cost per item p and the number of items made x, which is p + x = 25. We are asked to find the profit as a function of x, the value of x that maximizes profit, and the corresponding value of p that maximizes profit.
a) To find the profit as a function of x, we subtract the cost function C(x) from the revenue function. The revenue per item is p, so the revenue function is R(x) = px. Therefore, the profit function P(x) is given by P(x) = R(x) - C(x) = px - (15 + 2x) = px - 15 - 2x.
b) To find the value of x that maximizes profit, we need to find the critical points of the profit function. We take the derivative of P(x) with respect to x and set it equal to zero to find the critical points. Differentiating P(x) with respect to x gives dP/dx = p - 2 = 0. Solving for x, we get x = p/2. Therefore, the value of x that maximizes profit is x = p/2.
c) To find the corresponding value of p that maximizes profit, we substitute x = p/2 into the equation p + x = 25 and solve for p. Substituting p/2 for x gives p + p/2 = 25. Combining like terms, we have 3p/2 = 25. Solving for p, we get p = 50/3. Therefore, the value of p that maximizes profit is p = 50/3.
In summary, the profit as a function of x is P(x) = px - 15 - 2x, the value of x that maximizes profit is x = p/2, and the corresponding value of p that maximizes profit is p = 50/3.
Learn more about function here;
https://brainly.com/question/11624077
#SPJ11
It is believed that UMD students get less sleep, on average, than the general population. A survey of 500 UMD students is conducted generated a mean of 7.24 hours with a standard deviation of 1.93 hours. We want to compare this to the population distribution of sleep times that has a mean of 8.32 hours with a standard deviation of 1.24. The distribution to be used for this test would be:
Answers
Therefore, the distribution used for this test is the standard normal distribution (z-distribution).
To compare the sleep times of UMD students to the population distribution, a hypothesis test can be performed. Specifically, to test if UMD students get less sleep, a one-sample z-test can be conducted.
The distribution to be used for this test would be the standard normal distribution (also known as the z-distribution). This is because we are comparing the sample mean (7.24 hours) to the population mean (8.32 hours) and have information about the population standard deviation (1.24 hours).
By calculating the test statistic using the formula:
z = (sample mean - population mean) / (population standard deviation / √(sample size))
we can determine the z-value and compare it to the critical value from the standard normal distribution to assess the significance of the difference in sleep times between UMD students and the general population.
To know more about standard normal distribution,
https://brainly.com/question/17515506
#SPJ11
everyone in this neighborhood owns a car. George lives in this neighborhood. Therefore, George owns a car. This is an example of
a. universal instantiation
b. existential generalization
c. existential instantiation d.universal generalization
Answers
The given statement "Everyone in this neighborhood owns a car. George lives in this neighborhood. Therefore, George owns a car." is an example of universal instantiation.
Universal instantiation is a valid logical inference rule that allows us to infer a specific instance from a universal statement. It is based on the idea that if a statement applies to every member of a group or category, then it must also apply to a specific individual within that group.
In the given statement, the universal statement is "Everyone in this neighborhood owns a car." This statement asserts that every member of the neighborhood owns a car. By applying universal instantiation, we can infer that George, who is a member of this neighborhood, also owns a car. This inference is valid because George is part of the group described by the universal statement, and thus the statement applies to him as well.
To further understand this concept, let's break down the options provided:
a. Universal instantiation: This is the correct answer. It refers to the process of deriving a specific instance from a universally quantified statement.
b. Existential generalization: This rule allows us to infer the existence of at least one instance based on specific instances. It is not applicable to the given statement.
c. Existential instantiation: This rule allows us to introduce a new instance based on the existence of a specific instance. It is not applicable to the given statement.
d. Universal generalization: This rule allows us to infer a universally quantified statement from specific instances. It is not applicable to the given statement.
In conclusion, the example provided is an instance of universal instantiation because it derives a specific instance (George owning a car) from a universally quantified statement (everyone in the neighborhood owning a car).
To know more about group visit:
https://brainly.com/question/14355056
#SPJ11
What happens to the critical value for a chi-square test if the sample size is increased?
Answers
The critical value for chi-square test decreases as the size of the sample increases.
As sample size increases, absolute differences become a smaller and smaller proportion of the expected value
learn more about chi-square test here:
https://brainly.com/question/14501691
#SPJ1
Four years ago you invested some money at 10% interest. you now have $439.23 in the account. if the interest was compounded yearly, how much did you invest 4 years ago?
Answers
\(~~~~~~ \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+\frac{r}{n}\right)^{nt} \quad \begin{cases} A=\textit{accumulated amount}\dotfill & \$439.23\\ P=\textit{original amount deposited}\\ r=rate\to 10\%\to \frac{10}{100}\dotfill &0.1\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{yearly, thus once} \end{array}\dotfill &1\\ t=years\dotfill &4 \end{cases}\)
\(439.23=P\left(1+\frac{0.1}{1}\right)^{1\cdot 4}\implies 439.23=P(1.1)^4 \\\\\\ \cfrac{439.23}{1.1^4}=P\implies 399.3=P\)