PLEASE HELP!!!!! I"LL MARK AS BRAINLIEST!!!Tom conducted a drawing competition at school. He bought 5 boxes of colored pencils and spent $5.25 on drawing paper. However, more contestants entered than he expected, and he had to buy 2 more boxes of colored pencils. The total cost of the paper and pencils was $82.95. Identify the equation and solution that would help to find the cost of each box of pencils.
A. 5x + 2x + 5.25 = 11.10; $82.95
B. 5x − 2x + 5.25 = 82.95; $11.10
C. 5x − 2x + 5.25 = 82.95; $1.11
D. 5x + 2x + 5.25 = 82.95; $11.10
Answers
Related Questions
Please help me solve this problem.

Answers
Luckily, the integral is basically set up for you:
\(\displaystyle \int_{\theta=0}^{2\pi} \int_{\phi=\frac\pi4}^{\frac\pi2} \int_{\rho=2}^6 \cos(\phi) \, d\rho \, d\phi \, d\theta\)
Since the limits on every variable are constant, and we can factorize \(f(\rho,\theta,\phi) = f_1(\rho) f_2(\theta) f_3(\phi)\), we can similarly factorize the integrals. (This is a special case of Fubini's theorem, if I'm not mistaken.)
So the triple integral is equivalent to
\(\displaystyle \left(\int_0^{2\pi} d\theta\right) \left(\int_{\frac\pi4}^{\frac\pi2} \cos(\phi) \, d\phi\right) \left(\int_2^6 d\rho\right)\)
and each of these subsequent integrals are easy to compute:
\(\displaystyle \int_0^{2\pi} d\theta = \theta \bigg|_0^{2\pi} = 2\pi - 0 = 2\pi\)
\(\displaystyle \int_{\frac\pi4}^{\frac\pi2} \cos(\phi) \, d\phi = \sin(\phi) \bigg|_{\frac\pi4}^{\frac\pi2} = \sin\left(\frac\pi2\right) - \sin\left(\frac\pi4\right) = 1 - \frac1{\sqrt2} = \frac{2 - \sqrt2}2\)
\(\displaystyle \int_2^6 d\rho = \rho\bigg|_2^6 = 6 - 2 = 4\)
Taken together, the triple integral evaluates to
\(\displaystyle \int_{\theta=0}^{2\pi} \int_{\phi=\frac\pi4}^{\frac\pi2} \int_{\rho=2}^6 \cos(\phi) \, d\rho \, d\phi \, d\theta = 2\pi \times \frac{2-\sqrt2}2 \times 4 = \boxed{4\pi(2-\sqrt2)}\)
20 + 3 (7 + 4) + 5 + 2 (7 + 9)
Answers
Answer:
90
Step-by-step explanation:
i did the math hope this helps you out
How many tiles can fit in a rectangular floor with length 14 ft and width 6 ft if the the square tiles has an edge of 3/4 ft.
Answers
A rectangular floor with a length of 14 ft and a width of 6 ft, square tiles with an edge length of 3/4 ft, a total of 144 tiles can fit.
To determine how many square tiles can fit in a rectangular floor, we need to calculate the total number of tiles that can fit both horizontally and vertically.
Given:
Length of the rectangular floor = 14 ft
Width of the rectangular floor = 6 ft
Edge length of square tile = 3/4 ft
First, let's calculate the number of tiles that can fit horizontally:
Length of the rectangular floor / Edge length of square tile = 14 ft / (3/4 ft) = 14 ft × (4/3 ft) = 56/3 ft
Since we want a whole number of tiles, we need to round down or take the floor value:
Number of tiles horizontally = floor(56/3) = 18 tiles
Next, let's calculate the number of tiles that can fit vertically:
Width of the rectangular floor / Edge length of square tile = 6 ft / (3/4 ft) = 6 ft × (4/3 ft) = 24/3 ft
Again, we round down or take the floor value:
Number of tiles vertically = floor(24/3) = 8 tiles
To find the total number of tiles, we multiply the number of tiles horizontally by the number of tiles vertically:
Total number of tiles = Number of tiles horizontally × Number of tiles vertically = 18 tiles × 8 tiles = 144 tiles
Therefore, in a rectangular floor with a length of 14 ft and a width of 6 ft, square tiles with an edge length of 3/4 ft, a total of 144 tiles can fit.
for such more question on length
https://brainly.com/question/20339811
#SPJ8
has a perimeter of 52 feet. Let W be the width, L be the length, and P be
the perimeter, all with units in feet.
a. Given two sets of four rectangles, find one rectangle in each set that could have a
perimeter of 52 feet.
b. Which of the symbols W, L, and P are variables?
c. Which of the symbols W, L, and P are constants?
Answers
A rectangle that could have a perimeter of 52 feet is a 12 feet by 14 feet rectangle.
The symbols W and L are variables.
The symbol P is a constant.
How to calculate the perimeter of a rectangle?In Mathematics and Geometry, the perimeter of a rectangle can be calculated by using this mathematical equation (formula);
P = 2(L + W)
Where:
P represent the perimeter of a rectangle.W represent the width of a rectangle.L represent the length of a rectangle.By substituting the given side lengths into the formula for the perimeter of a rectangle, we have the following;
P = 2(L + W)
52 = 2(12 + 14)
52 = 2(26)
52 feet = 52 feet.
Read more on perimeter of a rectangle here: brainly.com/question/28695033
#SPJ1
What is the answer to this equation?

Answers
Answer:
OQ = 12
Step-by-step explanation:
PQ + OP = OQ
x + 7 + 4x - 10 = 4x
5x - 3 = 4x
x = 3
OQ = 4x = 4(3) = 12
A toy manufacturer wants to know how many new toys children buy each year. Assume a previous study found the standard deviation to be 1.8. She thinks the mean is 5.8 toys per year. What is the minimum sample size required to ensure that the estimate has an error of at most 0.12 at the 80% level of confidence
Answers
Answer:
\(n=(\frac{z_{\alpha/2} \sigma}{ME})^2\) (b)
The critical value for 80% of confidence interval now can be founded using the normal distribution the significance level would be 20% and the critical value \(z_{\alpha/2}=1.28\), replacing into formula (b) we got:
\(n=(\frac{1.28(1.8)}{0.12})^2 =368.64 \approx 369\)
So the answer for this case would be n=369 rounded up to the nearest integer
Step-by-step explanation:
We know the following info given:
\( \sigma = 1.8\) represent the standard deviation
\(\mu = 5.8\) the true mean that she believes
\( ME = 0.12\) represent the margin of error
The margin of error is given by this formula:
\( ME=z_{\alpha/2}\frac{s}{\sqrt{n}}\) (a)
And on this case we have that ME =+0.12 and we are interested in order to find the value of n, if we solve n from equation (a) we got:
\(n=(\frac{z_{\alpha/2} \sigma}{ME})^2\) (b)
The critical value for 80% of confidence interval now can be founded using the normal distribution the significance level would be 20% and the critical value \(z_{\alpha/2}=1.28\), replacing into formula (b) we got:
\(n=(\frac{1.28(1.8)}{0.12})^2 =368.64 \approx 369\)
So the answer for this case would be n=369 rounded up to the nearest integer
STAINED GLASS Pablo made the stained glass
window shown. He used an inscribed square and
equilateral triangle for the design.
a. Label the angle measures on the outer edge of the
triangle.
b. Label all of the arcs with their degree measure.

Answers
a) The angles outside the side PQ measure 65° and 25°
The angles outside the side QR measure 85° and 95°
The angles outside the side PR measure 55° and 35°
b) The arc PR, PQ and PR measure 120°
a)
Let us assume that the inscribed square be ABCD and equilateral triangle is PQR.
Let side PR of triangle intersects the quadrilateral at points M and N.
So, we get a triangle DMN outside the equilateral triangle.
Here, ∠DMN = 55°, ∠D = 90°
So, ∠MND = 180 - (90 + 55)
= 35°
Similarly, side PQ of triangle PQR intersects the quadrilateral at points X and Y.
So, we get a triangle AXY outside the equilateral triangle.
From triangle PXM we get the measure of angle PXM which is 65 degrees.
As angle PXM and angle AXY are opposite angles, the measure of angle AXY = 65°
∠A = 90°
So, ∠AYX = 180° - (∠A + ∠AXY )
= 180° - (90° + 65°)
= 25°
Let the side QR of triangle PQR intersects the quadrilateral at points L and K.
so we get new quadrilateral LKBC
In this quadrilateral ∠B = 90°, ∠C = 90°
From triangle QYL, we get the measure of angle QLY = 95°
So, the measure of ∠KLB = 95° .......(∠QLY and ∠KLB opposite angles)
So, the remaining angle LKC of quadrilateral LKBC would be,
∠LKC = 360° - (∠B + ∠C + ∠KLB)
∠LKC = 360° - (90 °+ 90° + 95°)
∠LKC = 85°
b)
We know that he angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
so, the measure of arc PR = 120°
the measure of arc PQ = 120°
the measure of arc RQ = 120°
Learn more about the triangle here:
https://brainly.com/question/14965331
#SPJ1

Sketch and label a net of the right triangular prism. Each square on the grid represents
1 square centimeter. Calculate the surface area of the prism by using its net.

Answers
The total surface area of the prism is determined as 216 cm².
What is the surface area of the prism?The surface area of the prism is calculated by applying the following formula.
The area of the two triangular faces is calculated as follows;
Area of the two triangles = 2 (¹/₂ x base x height )
Area of the two triangles = 2 (¹/₂ x 6 cm x 4 cm )
Area of the two triangles = 24 cm²
The area of rectangular faces is calculated as follows;
A = ( 5 cm x 12 cm ) + (5 cm x 12 cm ) + ( 6 cm x 12 cm )
A = 192 cm²
The total surface area of the prism is calculated as follows;
Area = 24 cm² + 192 cm²
Area = 216 cm²
The sketch of the triangular prism is in the image attached.
Learn more about surface area of prism here: https://brainly.com/question/16421693
#SPJ1

The length of a rectangular field is represented by the expression 14x-3x^2+2y . The width of the field is represented by the expression 5x-7x^2+7y . How much greater is the length of the field than the width?
Answers
The length of the field is greater than the width by the expression \((14x - 3x^2 + 2y) - (5x - 7x^2 + 7y).\)
1. The length of the field is represented by the expression \(14x - 3x^2 + 2y.\)
2. The width of the field is represented by the expression \(5x - 7x^2 + 7y\).
3. To find the difference between the length and width, we subtract the width from the length: (\(14x - 3x^2 + 2y) - (5x - 7x^2 + 7y\)).
4. Simplifying the expression, we remove the parentheses: \(14x - 3x^2 + 2y - 5x + 7x^2 - 7y.\)
5. Combining like terms, we group the \(x^2\) terms together and the x terms together: \(-3x^2 + 7x^2 + 14x - 5x + 2y - 7y.\)
6. Simplifying further, we add the coefficients of like terms:\((7x^2 - 3x^2) + (14x - 5x) + (2y - 7y).\)
7. The simplified expression becomes: \(4x^2 + 9x - 5y.\)
8. Therefore, the length of the field is greater than the width by the expression \(4x^2 + 9x - 5y.\)
For more such questions on length, click on:
https://brainly.com/question/28322552
#SPJ8
The diameter of a circle is multiplied by 10 how does the circumference change?
Answers
Step-by-step explanation:
The circumference of a circle is given by :
C=2πr, r is the radius of the circle
Also, 2r = D, diameter of the circle
⇒ C = πD
If the diameter of a circle is multiplied by 10, it means,
C = π(10)
⇒ C = 10π
Hence, if the diameter of a circle is multiplied by 10, then its circumference becomes 10π.
ANSWER FAST
NO LINKS
q>d, if d=3
Answers
Answer:
q = 4 or above
Step-by-step explanation:
"4 or above" means 4, 5, 6, 7.... so on. ">" means greater than, meaning any number that is on the bigger side of the symbol is greater/more than the number on the other side. Example:
q > d
4 > 3
5 > 3
THE TOPIC IS: AREA OF CIRCLES!! PLEASE HELP ME WITH THIS QUESTION!!! WHATS THE ANSWER?? I WILL GIVE YOU BRAINLIEST AND A THANKS!!! AND PLS PUT AN EXPLANATION!! THANK YOUU
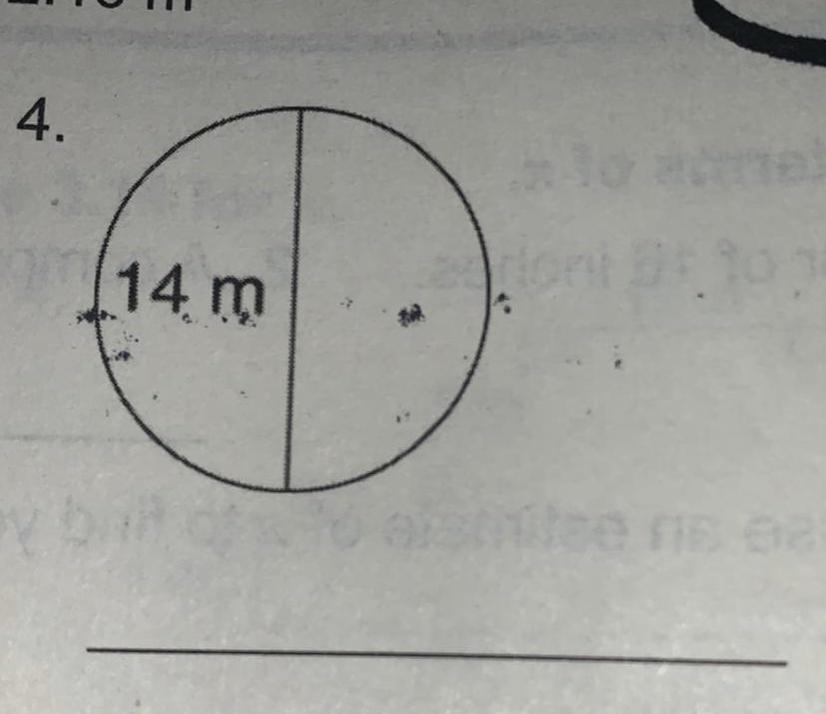
Answers
Answer:
Area: 153.86 m
Step-by-step explanation:
The formula for area of a circle is πr^2 (pi ⋅ radius ⋅ radius).
Here, only the diameter (14) is displayed.
To find the radius, we must divide the diameter by 2.
14/2 = 7
7 is the radius.
Now, we must plug in the numbers.
(3.14 is very commonly used for pi.)
pi ⋅ radius ⋅ radius
3.14 ⋅ 7 ⋅ 7 = 153.86.
Therefore, the area of this circle is 153.86 m.
Test the claim that the mean GPA of night students is significantly different than the mean GPA of day students at the 0.02 significance level.
GPA-Night GPA-Day 3.15 3.47 3.68 3.49 3.34 3.07 3.07 3.31 3.31 3.28 3.2 3.05 3.07 3.12 2.8 3.5 3.04 3.04 3.13 3.19 3.54 3.26 3.24 3.31 3.02 3.45 3.44 2.9 2.79 2.76 3.18 2.69 2.99 3.46 3.28 3.09 3.16 2.72 3.08 3.14 2.47 3.08 3.03 2.99 3.02 3.11 2.58 2.84 3.36 2.99 3.04 2.99
(1) The null and alternative hypothesis would be:
a.H0:μN≥μD
H1:μN>μD.
b.H0:μN=μD
H1:μN≠μD.
c.H0:pN≥pD
H1:pN
d.H0:pN=pD
H1:pN≠pD.
e.H0:μN≤μD
H1:μN<μD
f.H0:pN≤pD
H1:pN>pD.
(2) The test is:_______.
a. right-tailed.
b. two-tailed.
c. left-tailed.
(3) The sample consisted of 70 night students, with a sample mean GPA of 2.12 and a standard deviation of 0.08, and 70 day students, with a sample mean GPA of 2.08 and a standard deviation of 0.02
Answers
Answer:
Step-by-step explanation:
Test the claim that the mean GPA of night students is significantly different than the mean GPA of day students at the 0.02 significance level.
GPA-Night GPA-Day 3.15 3.47 3.68 3.49 3.34 3.07 3.07 3.31 3.31 3.28 3.2 3.05 3.07 3.12 2.8 3.5 3.04 3.04 3.13 3.19 3.54 3.26 3.24 3.31 3.02 3.45 3.44 2.9 2.79 2.76 3.18 2.69 2.99 3.46 3.28 3.09 3.16 2.72 3.08 3.14 2.47 3.08 3.03 2.99 3.02 3.11 2.58 2.84 3.36 2.99 3.04 2.99
(1) The null and alternative hypothesis would be:
a.H0:μN≥μD
H1:μN>μD.
b.H0:μN=μD
H1:μN≠μD.
c.H0:pN≥pD
H1:pN d.H0:pN=pD
H1:pN≠pD.
e.H0:μN≤μD
H1:μN<μD
f.H0:pN≤pD
H1:pN>pD.
(2) The test is:_______.
a. right-tailed.
b. two-tailed.
c. left-tailed.
(3) The sample consisted of 70 night students, with a sample mean GPA of 2.12 and a standard deviation of 0.08, and 70 day students, with a sample mean GPA of 2.08 and a standard deviation of 0.02
Add 2.5 to the product of 4.2 and 0.2
Answers
Answer:
3.34.
Step-by-step explanation:
4.2 * 0.2 + 2.5
= 0.84 + 2.5
= 3.34.
Answer:
3.34
Step-by-step explanation:
the product is 4.2×0.2=0.84
add is 2.5 + 0.84=3.34
PLEASE HELP ME, I DON'T UNDERSTAND!

Answers
Answer:
c
Step-by-step explanation:
We need to divide \(9x^2-6x+2\) by 3x -1
we know that 2 = 1+1 so
\((9x^2-6x+1)+1\)
if you notice the thing that it's inside the parenthesis it's a perfect square
\(((3x)^2-2(3x)+1)+1\\=(3x-1)^2+1\\\)
if we divide this by 3x -1 we get
\(\frac{(3x-1)^2+1}{3x-1} \\\\=\frac{(3x-1)^2}{3x-1}+\frac{1}{3x-1} \\\\=3x-1 + \frac{1}{3x-1}\)
so answe is c
For the class field trip, the fourth grades at Jefferson Elementary School need to take buses. Each bus fits 55 students and there are 200 students in fourth grade. How many buses will they need?
3 buses
3 R20 buses
4 buses
None of these is correct.
Answers
They will need 4 buses.
What is division?The division in mathematics is one kind of operation. In this process, we split the expressions or numbers into the same number of parts.
Given:
For the class field trip,
the fourth grades at Jefferson Elementary School need to take buses.
Each bus fits 55 students,
and there are 200 students in fourth grade.
The number of buses,
= 200/55
= 3.63
≈ 4.
Therefore, the need is for 4 buses.
To learn more about the division;
https://brainly.com/question/13263114
#SPJ2
A 39.2 g sample of copper took
up the 4.4 cm3 of space.
What is the density of the
copper piece in g/cm3?
[?] g/cm³
Record your answer to the tenths place.
Density (g/cm³)
![A 39.2 g sample of copper tookup the 4.4 cm3 of space.What is the density of thecopper piece in g/cm3?[?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/8va5sYZ9GKR3JjCzTRAyJCgT3FEp1CtJ.png)
Answers
The density of the copper piece is 17. 82g/cm³
How to determine the density
The formula for determining density is expressed as;
D = m/ v
Density is denoted with rho 'ρ'
Where;
m is the mass of the object = 39.2 g v is the volume occupied by the object = 4.4 cm³Substitute the values into the formula
Density, ρ = 39. 2/ 4. 4
Divide through
Density, ρ = 17. 82 g/cm³
The density of the copper piece is 17. 82g/cm³
Thus, the density of the copper piece is 17. 82g/cm³
Learn more about density here:
https://brainly.com/question/17780219
#SPJ1
Value of 3 to the power of 3 -8divided by 4
Answers
Answer: 25
Step-by-step explanation:
(3^3)-(8÷4)=25
Which of these numbers are greater than 24? Check all that apply.
O A. 12
B. 15
O C. 42
D. 41
E. 13
D F. 18
Answers
Answer:
A, B, E, F
Step-by-step explanation:
24>12, 24>15, 24>13, 24>18, 24<42, 24<41
Describe the end behavior of the given function.
F(x) = (2/3)^x - 2

Answers
Answer:
C. As x increases, f(x) approaches -2.
Answer:
C. As x increases, f(x) approaches -2. -----
Step-by-step explanation:
The vertex of this parabola is at (3,-2). When the x-value is 4, the
y-value is 3. What is the coefficient of the squared expression in the
parabola's equation?
O
O
A-1
B. 7
C. 1
D. 5
Answers
Answer:
5
Step-by-step explanation:
f(x) = a(x-3)² - 2
When x = 4, y = 3, so:
3 = a(4-3)² - 2
5 = a

Help I'm stuck on this question please help!

Answers
Answer:
A=20 degrees
Step-by-step explanation:
All of the interior angles of a triangle must add up to 180 degrees, so:
2x+5x+11x=180
18x=180
x=10
A=2(10)=20
Hope this helps!
Answer:
Angle A = 20 degrees
Step-by-step explanation:
The sum of the angles of a triangle is 180
A+ B+ C = 180
2x+5x+11x = 180
Combine like terms
18x = 180
Divide by 18
18x/18 = 180/18
x = 10
Angle A = 2x = 2*10 = 20
Angle B = 5x = 5*10 = 50
Angle C = 11x = 11*10 =110
For what value of n are the line y = 3x + 1 and y = nx - 4 perpendicular?
A -1
B 1/4
C 3
D -1/3
I’ll give brainly if you get the correct answer !!!
Answers
Answer:
D. -1/3
The slopes of perpendicular lines are negative reciprocals of each other. In other words, the product of the slopes of perpendicular lines is -1. So the slope of a line perpendicular to a line with a slope of 3 will have a slope of -1/3. D is correct.
How can you use mental math to multiply two numbers?
Answers
Answer: Break the numbers you're multiplying into parts.
Step-by-step explanation:
What I find helps is splitting up the numbers and later adding them back together. An example of this is:
29×14
First I'd do 29×10, and get 290
Then 20×4, followed by 9×4, resulting in 80 and 36 respectively
Finally, 290+80+36= 406
I find the simplest numbers in the problem (2,5,10,20, etc.) and multiply from there. This may not be the best trick, but this is what I find helps. I hope this may help you too, and I wish you the best of luck.
Which of the following steps were applied to ABCD to obtain A'B'C'D'?
A. shifted 3 units right and 4 units up
B. shifted 3 units right and 2 units up
C. shifted 2 units right and 3 units up
D. shifted 2 units right and 4 units up

Answers
ntit fl Kuta Software - Infinite Algebra 2 Vertex Form of Parabolas Use the information provided to write the vertex form equation of each parabola. 2) y=x² - 2x-5
Answers
We have
\(y=x^2-2x-5\)where
a=1
b=-2
c=-5
First we need to find the vertex, with the next formula we will find the x-coordinate of the vertex.
\(x=\frac{-b}{2a}\)we substitute the values
\(\begin{gathered} x=\frac{-(-2)}{2(1)} \\ x=\frac{2}{2} \\ x=1 \end{gathered}\)then we substitute the value of the x-coordinate in the original equation in order to find the y-coordinate
\(\begin{gathered} y=1^{2}-2(1)-5 \\ y=1-2-5 \\ y=-6 \end{gathered}\)the coordinates of the vertex is (1,-6)
the vertex form of the parabola is
\(y=a\mleft(x-h\mright)^2+k\)where h is the x-coordinate of the vertex and k is the y-coordinate of the vertex, the vertex form of this parabola is
\(y=(x-1)^2-6\)What would the height need to be for this curve to be a density curve?
1/5
1/4
1/2
1

Answers
For a curve to be a density curve, it must meet certain conditions such as it should be non-negative, and the area under the curve should equal 1. Furthermore, the curve should be continuous and smooth, and there should be no values outside the range of the data.
Let's see how the height would need to be for this curve to be a density curve.A density curve is a statistical representation of the distribution of a dataset or population. Density curves are used to describe the distribution of continuous data and provide a visual representation of the likelihood of an event occurring within a specific range of values. It helps to determine the proportion of data that falls within a given range of values. A density curve is used to provide a graphical representation of data without showing the individual data points.To be a density curve, a curve must have the following properties:The curve should be non-negative.The area under the curve should be equal to 1.The curve should be smooth and continuous.There should be no values outside the range of the data.From the above properties, we can conclude that the height required for a curve to be a density curve depends on the data that the curve represents. As long as the curve meets the above conditions, it can be considered a density curve. So, there is no specific height required for a curve to be a density curve. The height of the curve can vary depending on the range of the data and the distribution of the data.For such more question on properties
https://brainly.com/question/30339264
#SPJ8
y is directly proportional to x^ . if y=12 when x=2 find, y when x=5
Answers
Answer:
The value of y = 30 when x = 5
Step-by-step explanation:
We know that when 'y' varies directly proportional to 'x', we get the equation
y ∝ x
y = kx
k = y/x
where k is called the 'constant of direct variation'.
We are given
y = 12 when x = 2
so substituting y = 12 and x = 2 in the equation
k = y/x
k = 12/2
k = 6
Thus, the value of k = 6
We have to determine the value of y when x = 5
so substitute x = 5 and k = 6 in the equation
y = kx
y = 6(5)
y = 30
Therefore, the value of y = 30 when x = 5
......................................................
Answers
Answer:
..............................................yes
Step-by-step explanation:
lol
n more than 12
A) n/12
B) 12 +n
C) 22
D) 12-n
Answers
Answer:
B) 12 +n
Step-by-step explanation:
"More than" is a key word.
Whenever you see more than, you are adding.