Answers
The solution to the inequality (g/20) ≤ 5 is given as follows:
B. g ≤ 100.
How to solve the inequality?The inequality in the context of this problem is defined as follows:
(g/20) ≤ 5.
We solve the inequality similarly to an equality, isolating the desired variable. The difference is that we obtain a range with infinity values, instead of a single value as is the case for an equality.
The multiplication is the inverse operation of the division, hence the solution is given as follows:
g ≤ 20 x 5.
g ≤ 100.
More can be learned about inequalities at https://brainly.com/question/25275758
#SPJ1
Related Questions
Which equation represents a circle that contains the point (–5, –3) and has a center at (–2, 1)?
Distance formula: StartRoot (x 2 minus x 1) squared + (y 2 minus y 1) squared EndRoot
(x – 1)2 + (y + 2)2 = 25
(x + 2)2 + (y – 1)2 = 5
(x + 2)2 + (y – 1)2 = 25
(x – 1)2 + (y + 2)2 = 5
Answers
Answer:
(x + 2)² + (y - 1)² = 25
Step-by-step explanation:
radius: r² = (1 - (-3))² + (-2 - (-5))² = 16 + 9 = 25
r = 5
Circle: (x - h)² + (y - k)² = r²
center: (-2 , 1) h = -2 k = 1
(x + 2)² + (y - 1)² = 25
The equation represents a circle that contains the point (–5, –3) and has a center at (–2, 1) is (x+2)^2 + (x-1)^2 = 25
Equation of a circleThe standard equation of a circle is expressed as:
(x-a)^2+(y-b)^2 = r^2
where:
(a, b) is the centre
r is the radius
Given the following parameters
(a, b) = (-2, 1)
r² = (1 - (-3))² + (-2 - (-5))² = 16 + 9 = 25
Substitute into the formula to have:
(x-(-2))^2 + (x-1)^2 = 25
(x+2)^2 + (x-1)^2 = 25
Hence the equation represents a circle that contains the point (–5, –3) and has a center at (–2, 1) is (x+2)^2 + (x-1)^2 = 25
Learn more om equation of a circle here: https://brainly.com/question/1506955
If you are doing a gift exchange, and everyone has to spend at least 10 dollars but less than 20 dollars, what inequality represents the situation
Answers
Answer:
10≥x<20
Step-by-step explanation:
what is the probability that a high school junior will take less than 135 minutes to complete the sat exam?
Answers
The probability that a high school junior will take less than 135 minutes to complete the SAT exam is 0.5745.
To determine the probability, the standard normal distribution table or calculator is utilized.
The standard normal distribution table, also known as the z-score table, is used to find the probability of a certain z-score or a range of z-scores.
The SAT exam's time is normally distributed, with a mean of 150 minutes and a standard deviation of 25 minutes.The formula for z-score is as follows:
z=(x-μ)/σ
Where x is the time to complete the SAT exam, μ is the mean of the time to complete the SAT exam, and σ is the standard deviation of the time to complete the SAT exam.
To calculate the z-score, the time of 135 minutes is substituted for x, the mean μ of 150 minutes is substituted for μ, and the standard deviation σ of 25 minutes is substituted for σ.The computation is as follows:
z=(135-150)/25= -0.60
Using the standard normal distribution table, the probability of getting a z-score of -0.60 is 0.2743.
To obtain the probability that a high school junior will complete the SAT exam in less than 135 minutes, the area under the standard normal curve to the left of z = -0.60 must be computed. Because the normal curve is symmetrical, the region to the right of z = -0.60 is equal to 1 - 0.2743 = 0.7257.
Finally, to obtain the region to the left of z = -0.60, 0.7257 must be subtracted from 1:1 - 0.7257 = 0.2743
for such more question on probability
https://brainly.com/question/24756209
#SPJ11
PLEASE HELP ME ASPA What is the equation of the line that has a slope of -4 and passes through the point (2, 3)? y = -4x + 5 y = -4x – 5 y = -4x + 11 None of these choices are correct.
Answers
Answer:
Third option is the right choice.
Step-by-step explanation:
y = -4x + 11 (Slope = m = -4)
3 = -4(2) + 11
3 = -8 + 11
3 = 3
True.
g(z) = 3z + 8
g(2w) =
Answers
Answer:
\(g(2w)=6w+8\)
Step-by-step explanation:
We know that \(g(z)=3z+8\)
And we want to find \(g(2w)\)
So, we will simply substitute 2w for z. This yields:
\(g(2w)=3(2w)+8\)
Distribute. Therefore:
\(g(2w)=6w+8\)
Which value below shows the strongest correlation?
A. 0.72
B. 0.35
C. 0.91
D. 0.99
E. 0.88
F. 0.29
G. 0.06
H. -0.55
Answers
Answer:
The answer is D. = 0.99
Jason is flying a kite and has 325 feet of kite string out. The angle of elevation between Jason’s hand and the kite string is 58˚. Jason’s hand is 3 feet above the ground. How high is the kite to the nearest tenth?
i need this asap pls
Answers
Answer:
The height of the kite is approximately 278.6 feet
Step-by-step explanation:
The length of Jason's Kite string, l = 325 feet
The angle of elevation of the kite string, θ = 58°
The height of Jason's hand, h = 3 feet above the ground
Therefore, we have;
The height of the kite = The vertical component of the length of the kite string + The height of Jason's hand above the ground
The height of the kite = l × sin(θ) + h
Substituting the values, we get
The height of the kite = 325 × sin(58°) + 3 ≈ 278.6 (which is obtained by rounding the answer to the nearest tenth)
The height of the kite ≈ 278.6 feet.
25/12 answer with a decimal please, thank you!
Answers
Answer: 20.8
Step-by-step explanation: .
what is the volume of the cylinder shown below to the nearest hundredth of a cubic meter 3.5 m w 2 m height
Answers
Answer:
The answer is 76.97
Step-by-step explanation:
The formula that I used
V=πr^2h
Volume = π·3.52·2 ≈ 76.96902
Answer:76.93
Step-by-step explanation:
Which of the following is a rational function?
A.
B.
C.
D.

Answers
Answer:
c
Step-by-step explanation:
c will be the answer g g g t g
Give a recursive definition of 3: (a) the set of even positive integers. (b) The set of positive integer powers of 4. (c) The set of polynomials with integer coefficients.
Answers
a) The set of even positive integers can be defined recursively as follows: Let X be the set of all even positive integers. Then, 2 is in X and if n is in X, then (n + 2) is in X. This definition is recursive because it is defined in terms of itself.
b) The set of positive integer powers of 4 can be defined recursively as follows: Let Y be the set of all positive integer powers of 4. Then, 4 is in Y and if n is in Y, then (4n) is in Y. This definition is recursive because it is defined in terms of itself.
c) The set of polynomials with integer coefficients can be defined recursively as follows: Let Z be the set of all polynomials with integer coefficients. Then, the constant polynomial 0 is in Z and if p and q are in Z, then (p + q) and (pq) are in Z. This definition is recursive because it is defined in terms of itself.
To know more about integers visit:
https://brainly.com/question/490943
#SPJ11
on average, an individual's bmr decreases approximately 3 to 5 percent per decade after what age? a. 20 b. 50 c. 30 d. 70
Answers
An individual's BMR decreases approximately 3 to 5 percent per decade on an average after the age of option C. 30.
BMR is known as basal metabolic rate which decreases when the age of a person increases.As metabolism factor slow down with the increase in age.After the age of 30 metabolism rate decreases which effect basal metabolic rate every decade by round about 3 to 5 percent.At the young age expenditure of the daily energy is quiet more compare to older age.On an average after the age of 30 BMR is decreases approximately by 3 to 5 percent.
Therefore, on an average individuals BMR is approximately decreases by round about 3 to 5 percent per decade after the age of option c. 30.
Learn more about average here
brainly.com/question/24057012
#SPJ4
In 33,291 how is the value of the three in the 10,000s place related to the value of the three in the thousands place
Answers
The place value of 3 in 10,000s place is the product of 10 with the place value of 3 in thousands place.
What is Place Value?Every digit in a number has it's own place value. Place value is the position of a digit in a number.
For example, in the number 3456, 6 is in the ones place, 5 is in the tens place, 4 is in the hundreds place and 3 is in the thousands place.
Given the number 33,291.
Place value of 1 = 1
Place value of 9 = 90
Place value of 2 = 200
Place value of 3 in thousands place = 3000
Place value of 3 in ten thousands place = 30,000 = 3000 × 10
That is, place value of 3 in 10,000s place is the product of ten with the place value of 3 in thousands place.
Hence the place value of 3 in thousands place multiplied to 10 gives the place value of 3 in 10,000s place.
Learn more about Place Values here :
https://brainly.com/question/27734142
#SPJ1
53 – 10 + 6y – 8y
How do I simplify this
Answers
Answer:
Step-by-step explanation:
Combine like terms.
53 and 10 are like terms.
6y , 8y are like terms
53 - 10 + 6y - 8y = 43 - 2y
Jaime is a pet groomer and charges $30 for an initial consultation, then $40 per hour to groom a pet. Jon charges only $50 per hour to groom a pet. In how many hours will the two groomers change the same price?
Answers
Answer:
3 hoursStep-by-step explanation:
let us first model the amount that Jaime and Jon will charge
let the total amount be y and let the number of hours be x
Jaime will charge
y=30+4x------1
Jone will charge
y=50x-----2
equating 1 and 2 we can solve for x which is the number of months Jaime and Jon will charge the same price
50x=30+40x
50x-40x=30
10x=30
divide both sides by 10 we have
x=30/10
x=3
2)write the equation represented by the algebra tiles

Answers
Answer:
4x+6=-6
Step-by-step explanation:
Bell Work
You Do
Camspite A is 5 miles north and 2 miles east of a ranger station.
Campsite B is 8 miles north and 6 miles east of the ranger station.
How far is Campsite A from Campsite B?
A 1 mi
B 5 mi
7 mi
25 mi
Answers
7 i do not feel like explaining tbh
which expression is equivalent to 2^3 square root x^2 • square root 16x if x > 0

Answers
Answer:
A
Step-by-step explanation:
The question is actually: 2 \sqrt[3]{x^3} ·\sqrt{16x}

The expression is equivalent to option A, \(\rm 8x \sqrt[6]{x}\).
What is an Expression?An expression is a mathematical statement that consists of variables, constants, and mathematical operators.
The expression is \(\rm 2\sqrt[3]{x^2} . \sqrt{16x}\)
The expression can be simplified as
\(\rm = 2 . 4 x^{2/3} x^{1/2}\\\\\=8 x ^{ 7/6}\\\\\\ = 8x x^{1/6}\\\\= 8x \sqrt[6]{x}\)
Therefore, the expression is equivalent to option A, \(\rm 8x \sqrt[6]{x}\).
To know more about Expression
https://brainly.com/question/14083225
#SPJ2
What is the end behavior of the function f(x)=8x^5-3x^3 +8x+5
Answers
Answer:
x → +∞, y → +∞
x → -∞, y → -∞
Step-by-step explanation:
The trick to identify its behavior is to determine the degree of the function and the coefficient of the term with the highest exponent.
Negative coefficient and odd degree (x → +∞, y → -∞) (x → -∞, y → +∞).Negative coefficient and even degree (x → +∞, y → -∞) (x → -∞, y → -∞).Positive coefficient and odd degree (x → +∞, y → +∞) (x → -∞, y → -∞).Positive coefficient and even degree (x → +∞, y → +∞) (x → -∞, y → +∞).The point (–5, 6) is located in which quadrant?
A coordinate plane.
Quadrant I
Quadrant II
Quadrant III
Quadrant IV

Answers
Answer:
b
Step-by-step explanation:
the radius of a sphere is increasing at a constant rate of 8 meters per second. at the instant when the radius of the sphere is 22 meters, what is the rate of change of the volume? the volume of a sphere can be found with the equation v
Answers
So, on solving the provided question we can say that the rate of change of the volume with respect to radius = \(1770 = 4/3 \pi r^3S = 4 \pi r^2\) \(dS/dt = 8 \pi r dr/dt\)
what is radius?The length of a circle or sphere, in more contemporary use, is the same as its radius in classical geometry, which is one of the line segments from its center to its circumference. The Latin word radius, which also refers to the spokes of a wagon wheel, gave rise to the term. The distance a circle's center is from any point on its perimeter is its radius. Usually, "R" or "r" is used to indicate it. A radius is a line segment that has one endpoint in the center and one on the circumference of a circle. Circular diameter equals radius The diameter of a circle is the segment that traverses its center and has ends that are on the circle.
Taking the derivative of the volume formula
\(DV/dt = 4\pi r*2 dr/dt\\5471 = 4 \pi r*2 dr/dt\)
This equation r and dr/dt
We can solve for r...
sphere is 1770 cubic inches
\(1770 = 4/3 \pi r^3S = 4 \pi r^2dS/dt = 8 \pi r dr/dt\)
To know more about radius visit:
https://brainly.com/question/28946570
#SPJ4
PLEASE someone help me

Answers
Answer:
Step-by-step explanation:
So the measurement given in this triangle is 74 degrees and both the sides of x is parallel, so-
74 + x + x = 180 ( angle sum property)
74 + 2x = 180
2x = 180 - 74
2x = 106
x = 106 divided by 2
x = 53
solve 4x^2 +x-3 using the box method
Answers
Answer:
(4x - 3)(x + 1)
Step-by-step explanation:
=4x² + x - 3
=4x² + 4x - 3x - 3
=4x(x + 1 ) - 3( x + 1)
=(4x - 3)(x + 1)
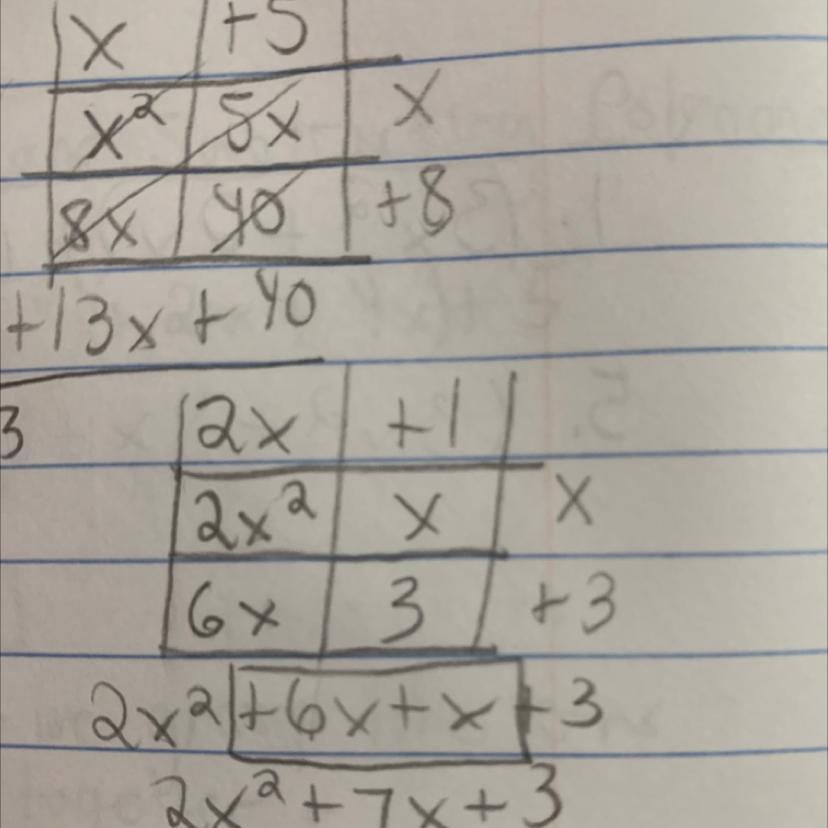
The diameter of a circular cookie cake is 14 inches. How many square inches make up half of the cookie cake? Approximate using π = 3.14.
615.44 square inches
307.72 square inches
153.86 square inches
76.93 square inches
Answers
The area in square inches that makes up half of the cookie cake is 615.44 square inches.
Given that the diameter of the circular cookie cake is 14 inches. The area of a circle is given as πr², here r is the radius of the circle.
The area of the half of the cookie cake is:
Area of the half of the cookie cake = π × r²
= π × (14 inches)²
= π × (14 inches)²
= 615.44 square inches
Hence, the area is 615.44 square inches.
Learn more about the Area here:
https://brainly.com/question/27683633
#SPJ1
Function f is a linear function and function g is defined by g(x) = f(x) + k. If the value of k is 7, how does the graph of g compare with the graph of f ?..
The graph of g is the graph of f
translated up 7 units
translated left 7 units
translated right 7 units
translated down 7 units
stretched vertically by a scale factor of 7
stretched horizontally by a scale factor of 7
Answers
The graph of g is Transformation up 7 units.
what is Transformation?
A graph transformation is a method for altering an existing graph or graphed equation to create a different version of the graph that follows. The modification of algebraic equations is a typical form of algebraic issue.
solution:
From the question, we have the following parameters that can be used in our computation:
g(x) = f(x) + k
Also, we have the value of k to be
k = 7
From the question, we can interpret g(x) = f(x) + k as f(x) is shifted up by k units
This means that
g(x) = f(x) + k
So, we have
g(x) = f(x) + 7
Hence, the transformation is (a) translated up 7 units
To learn more about Transformation from the given link
https://brainly.com/question/1620969
#SPJ1
cooper 12.1.13 an artery has a circular cross section of radius 5 millimeters. the speed at which blood flows along the artery fluctuates as the heart beats. the speed after t seconds is meters per second. (a)sketch on graph paper a graph of the speed over a 3 second time span. (b)what volume of blood passes along the artery in one second? v
Answers
(a) To sketch a graph of the speed over a 3-second time span, we need to know the equation that describes the relationship between speed and time. Without this information, we cannot create an accurate graph.
(b) To find the volume of blood that passes along the artery in one second, we need to use the formula Q = A * v, where Q is the flow rate, A is the cross-sectional area of the artery, and v is the speed of blood flow. The cross-sectional area of the artery is given by A = pi * r^2, where r is the radius of the artery.
Thus, substituting the given values, we get:
A = pi * (5mm)^2 = 78.54 mm^2
v = 0.2 + 0.1 sin(2pit/0.8) (using the given information)
Q = A * v = 78.54 * (0.2 + 0.1 sin(2pit/0.8))
To find the volume of blood that passes along the artery in one second, we need to evaluate Q at t = 1 second, so we get:
Q = 78.54 * (0.2 + 0.1 sin(2pi1/0.8)) = 31.39 mm^3/s
Therefore, the volume of blood that passes along the artery in one second is approximately 31.39 cubic millimeters.
For more questions like Volume click the link below:
https://brainly.com/question/16931624
#SPJ4
jabari is thinking of three numbers. The
greatest number is 3 times than the middle
number. The smallest number is 5 less the
middle number. The sum of the three
numbers is 35. Find the numbers
Answers
Answer:
3, 8 and 24.
Step-by-step explanation:
Let's write some equations that satisfy this problem (x = smallest, y = middle, z = largest):
z = 3y
x + y + z = 35
x = y - 5
We can use substitution to solve this problem! I will take x + y + z = 35, replace x with y - 5 (since we know x = y - 5) and replace z with 3y (since we know z = 3y).
This leaves us with:
(y - 5) + y + (3y) = 35
y - 5 + y + 3y = 35
5y - 5 = 35
5y = 40
y = 8
Since we know y (the middle number) is 8, we can now find the other numbers:
Largest is 3 times the middle, so 8 * 3 = 24.
Smallest is 5 less than the middle, so 8 - 5 = 3.
The 3 numbers are therefore 3, 8 and 24.
number whose square root and cube root are equal.
Answers
Answer:
The numbers are 0 and 1
MARK ME AS BRAINLIEST
This is kind of off topic for math but I still need to know the answer, so I’ve finished all my math work and I know my work is also correct but for some reason my grades drop down. I don’t understand why...
Answers
Answer:
email or call or talk to your teacher and ask why
Step-by-step explanation:
Find the equation of a line parallel to y + 9 = -3/2x that passes through the point (-8,9)

Answers
slope intercept form:
y = mx + b (where m = slope
and b = y-intercept)
simply subtract 9 from both sides of the given equation to get slope intercept form of the first line:
y + 9 = -3/2x
y + 9 - 9 = -3/2x - 9
y = -3/2x - 9
so the slope (m) = -3/2
the problem tells us a point on the second line (x,y) or (-8,9)
and we now know slope is -3/2
so let’s plug those in and solve for the y-intercept (b) of the second line.
y = mx + b
9 = -3/2(-8) + b
9 = 12 + b
9 - 12 = 12 - 12 + b
-3 = b
so now we know the slope (m) of both lines is -3/2 and the y-intercept (b) of the second line is -3
all we have to do is use the information to establish slope intercept form of the equation of the second line:
y = mx + b
y = -3/2x - 3
The answer is: y = -3/2x - 3
check your answer by plugging the point (-8,9) back in to your equation
9 = -3/2(-8) - 3
9 = 12 - 3
9 = 9 [TRUE]
