Answers
Answer:
-3
Step-by-step explanation:

Related Questions
find an equation of the curve that passes through the point (0, 1) and whose slope at (x, y) is 5xy. (note: start your answer with y
Answers
The equation of the curve that passes through the point (0, 1) and has a slope of 5xy at any point (x, y) is y = (5/2) * x^2y + 1. This equation represents a curve where the y-coordinate is a function of the x-coordinate, satisfying the conditions.
To determine an equation of the curve that satisfies the conditions, we can integrate the slope function with respect to x to obtain the equation of the curve. Let's proceed with the calculations:
We have:
Point: (0, 1)
Slope: 5xy
We can start by integrating the slope function to find the equation of the curve:
∫(dy/dx) dx = ∫(5xy) dx
Integrating both sides:
∫dy = ∫(5xy) dx
Integrating with respect to y on the left side gives us:
y = ∫(5xy) dx
To solve this integral, we treat y as a constant and integrate with respect to x:
y = 5∫(xy) dx
Using the power rule of integration, where the integral of x^n dx is (1/(n+1)) * x^(n+1), we integrate x with respect to x and get:
y = 5 * (1/2) * x^2y + C
Applying the initial condition (0, 1), we substitute x = 0 and y = 1 into the equation to find the value of the constant C:
1 = 5 * (1/2) * (0)^2 * 1 + C
1 = C
Therefore, the equation of the curve that passes through the point (0, 1) and has a slope of 5xy at any point (x, y) is:
y = 5 * (1/2) * x^2y + 1
Simplifying further, we have:
y = (5/2) * x^2y + 1
To know more about equation of the curve refer here:
https://brainly.com/question/31467851#
#SPJ11
Given a mean of 80 and a standard deviation of 3, label the normal curve below.

Answers
Answer:
The points from the left;
71, 74 , 77, 80, 83, 86 , 89
Step-by-step explanation:
Here, we want to label the normal curve given the mean and the standard deviation
From what we have, the central part is the mean while the other parts are deviations from the mean
We will label the graph starting from the left to the right
1 is 3 SD from the mean (negatively)
That will be 80-3(3) = 80-9 = 71
2 is 2 SD away
That will be;
80 -2(3) = 80-6 = 74
The 3rd part is 1 SD away
That will be 80-3 = 77
The midpoint is for the mean which is 80
The point after this will be;
80 + 3 = 83
The point after this will be;
83 + 3 = 86
Next is
86 + 3 = 89
Find the y-intercept of the line y=2x–12. Write your answer as an integer or as a simplified proper or improper fraction, not as an ordered pair.
Answers
Answer:
b = -12
Step-by-step explanation:
In order to find the y intercept, the equation of the line must be in slope intercept form \(y=mx+b\) where m is the slope and b is the y intercept.
\(y=2x-12\)
As we can see, the equation of the line is clearly in slope intercept form. If we know click clack, aka change the sign and change if its positive or negative, 12 becomes -12.
Therefore, the y intercept is -12.
PLEASE HELP ME ASAP (picture attached)
7.
A circle with a radius of 9 cm is divided into five equal sectors.
The diagram shows one of the sectors, AOB.
The chord AB is drawn.
B
9 cm
A
72
Find the area of the shaded region.

Answers
im learning this in maths too but my maths teacher said
"tita=a times by πr²over 360 divided by angle then times by 18 cuz diameter=1 but radius is half of diameter
i am so sorry if this doesnt work
A square garden has an area of 5 square feet. Without using a calculator, find the side length of the garden to the nearest tenth of a foot
Answers
Answer:
2.23
Step-by-step explanation:
tune able to find the area you should x one side by the other side to find the area 2.23 * 2.23 equals close to 5 square feet
According to the Guinness Book of World Records, a woman from Russia, Mrs. Vassilyeva, had 69 children between the years 1725 to 1765. She had 16 pairs of twins, 7 sets of triplets, and 4 sets of quadruplets. Suppose one of the births is randomly selected. Given that Mrs. Vassilyeva gave birth to at least 3 children (triplets), what is the probability that she gave birth to quadruplets?
(A) 4/27
(B) 7/11
(C) 3/11
(D) 3/27
(E) 4/11
Answers
The probability that Mrs. Vassilyeva gave birth to quadruplets, given that she gave birth to at least 3 children, is 16/69, which is closest to option A.
Out of the 69 children Mrs. Vassilyeva had, there were 16 x 2 = 32 twins, 7 x 3 = 21 triplets, and 4 x 4 = 16 quadruplets. This means that the total number of births was,
32 + 21 + 16 = 69
If we randomly select one of these births, the probability that it is a quadruplet is,
P(quadruplet) = 16/69
Given that Mrs. Vassilyeva gave birth to at least 3 children (triplets), this means that the number of possible births that could have been selected is 21 + 16 = 37. Therefore, the probability that the selected birth was a quadruplet, given that Mrs. Vassilyeva gave birth to at least 3 children, is,
P(quadruplet | at least 3 children) = P(quadruplet and at least 3 children) / P(at least 3 children)
We know that P(quadruplet and at least 3 children) is simply the probability of selecting a quadruplet, which is 16/69. To find P(at least 3 children), we need to find the probability of selecting a triplet, a quadruplet, or one of the remaining 69 - 21 - 16 = 32 births that were not triplets or quadruplets,
P(at least 3 children) = P(triplet) + P(quadruplet) + P(other births)
P(triplet) = 21/69
P(other births) = 32/69
Therefore P(at least 3 children) = 21/69 + 16/69 + 32/69 = 69/69 = 1
Plugging in these values, we get,
P(quadruplet | at least 3 children) = (16/69) / 1 = 16/69
Therefore, the answer is not one of the given options. However, the closest option is (A) 4/27, which is the same as 16/69 rounded to the nearest hundredth.
To know more about probability, visit,
https://brainly.com/question/13604758
#SPJ1
What are 2 equations /ratios you could write to solve for a? Do not solve just write the equations you used to solve
Answers
This equation represents a proportion where the sum of "a" and 2 is related to the fraction 6/3. By cross-multiplying and solving for "a," we can determine its value.
To solve for variable "a," we need two equations or ratios that involve "a" and other known variables. Without specific context or information, it's challenging to provide concrete equations. However, I can provide two general equations or ratios that you could potentially use to solve for "a" in different scenarios.
Equation 1: Proportion equation
In many situations, proportions are used to solve for unknown variables. If we have a proportion involving "a," we can set up an equation and solve for it.
For example, let's say we have the proportion:
(a + 2) / 4 = 6 / 3.
This equation represents a proportion where the sum of "a" and 2 is related to the fraction 6/3. By cross-multiplying and solving for "a," we can determine its value.
Equation 2: Linear equation
In some cases, we may have a linear equation involving "a" and other variables. This equation could be derived from a given relationship or pattern.
For instance, suppose we have the linear equation:
3a - 2b = 10.
This equation represents a relationship between "a," "b," and a constant term. By rearranging the equation and isolating "a," we can solve for its value in terms of the other variables and the constant.
These are just two general examples of equations or ratios that could be used to solve for "a." The specific equations or ratios you use will depend on the given context, problem, or relationship between variables. It's important to tailor the equations to the specific problem at hand in order to obtain an accurate solution for "a."
for more such question on equation visit
https://brainly.com/question/17145398
#SPJ8
The following two-way table shows the distribution of high school students categorized by their grade level and music-listening preference.
A 4-column table with 3 rows. Column 1 has entries junior, sophomore, total. Column 2 is labeled Earbuds with entries 4, 4, 8. Column 3 is labeled Speakers with entries 12, 12, 24. Column 4 is labeled total with entries 16, 16, 32. The columns are titled music-listening preferences and the rows are titled grade level.
Suppose a high school student is selected at random. Let event A = junior and event B = earbuds. Are events A and B independent?
Yes, P(A) = P(A|B).
Yes, P(A) = P(B|A).
No, P(A) ≠ P(A|B).
No, P(A) ≠ P(B|A).

Answers
The correct statement regarding whether juniors and earbuds are independent events are given as follows:
Yes, because P(A|B) = P(A).
What are independent events?If two events are independent, the multiplication of the probabilities of each event is equals to the probability of both events, that is:
P(A and B) = P(A) x P(B).
The conditional probability formula is given as follows:
P(B|A) = P(A and B)/P(A).
Hence, for independent events, we have that:
P(B|A) = P(B).
And also:
P(A|B) = P(A).
A probability of an event is calculated as the division of the number of total outcomes by the number of desired outcomes.
Out of 32 students, 16 are juniors, hence the probability of a junior student is given as follows:
P(A) = 16/32 = 0.5.
Out of 8 students with earbuds, 4 are juniors, meaning that the conditional probability is given as follows:
P(A|B) = 4/8 = 0.5.
As the probability is equal, these two events are independent, and the first statement is correct.
More can be learned about independent events at https://brainly.com/question/30144140
#SPJ1
Please help me!
Find the value of x for the rectangle.

Answers
Answer:
36
Step-by-step explanation:
Dennis is up to bat during his softball game. he swings his bat 261 degrees in 0.75 seconds before contacting the ball. he makes contact with the ball 57 cm down the bat (away from the axis of rotation). what is the linear velocity of the ball after contact with the bat? (please put the answers in meters)
Answers
Answer:
here is answer
Step-by-step explanation:
To find the linear velocity of the ball after contact with the bat, we need to convert the angular velocity to linear velocity.
Given:
Angular displacement (θ) = 261 degrees
Time (t) = 0.75 seconds
Distance from axis of rotation (r) = 57 cm
First, we convert the angular displacement from degrees to radians:
θ (in radians) = (261 degrees) × (π/180)
≈ 4.5539 radians
Next, we calculate the angular velocity (ω):
ω = θ / t
= 4.5539 radians / 0.75 seconds
≈ 6.0719 radians/second
To convert the distance from the axis of rotation to meters:
r (in meters) = 57 cm × (1 meter / 100 centimeters)
= 0.57 meters
Now, we can calculate the linear velocity (v) using the formula:
v = ω × r
v ≈ 6.0719 radians/second × 0.57 meters
v ≈ 3.4649 meters/second
Therefore, the linear velocity of the ball after contact with the bat is approximately 3.4649 meters/second.
Composition of functions:determine the equation of (gof)(x) image attached much appreciated

Answers
In general, the definition of the function composition is given by the expression below
\((g\circ f)(x)=g(f(x))\)Therefore, in our case,
\((g\circ f)(x)=g(-\frac{1}{\sqrt{x}})=1(-\frac{1}{\sqrt{x}})^3+19(-\frac{1}{\sqrt{x}})^2+16=-\frac{1}{x^{\frac{3}{2}}}+\frac{19}{x}+16\)Then, the answer is\(\Rightarrow(g\circ f)(x)=-\frac{1}{x^{\frac{3}{2}}}+\frac{19}{x}+16\)Answer? Please make sure you answer it as a simplified fraction.

Answers
==================================================
Work Shown:
Let x = 0.363636...
The "36" pattern goes on forever as indicated by the three dots.
Multiply both sides by 100 to get 100x = 36.363636...
Effectively, multiplying by 100 moves the decimal point over 2 spots to the right. The "36" goes on forever here too. The key is to match up the infinite sequences of "36"s and cancel them out through subtraction
36.363636... - 0.363636... = 36
while
100x - x = 99x
So after subtracting the equations, we end up with 99x = 36
From here we solve for x by dividing both sides by 99 and reducing the fraction
99x = 36
x = 36/99
x = (9*4)/(9*11)
x = 4/11
As a check, use your calculator to find that
4/11 = 0.36363636...
so the answer is confirmed
Note: your calculator may display something like 0.3636363636364, that 4 should not be there. It's a result of rounding (due to the next digit being a 6). Keep in mind that rounding error is often a possibility when it comes to approximate calculations. The calculator only has so much memory and display space.
Step 1: Calculate the measures of center for Mrs. Hampton's data in the dot plot (round your answer to the nearest tenths place). Show your work and briefly explain each step. (Measures of Center are the Mean and Median of a data set)
Answers
*dot plot is shown in the attachment below
Answer:
Mean = 6.3
Median = 6
Step-by-step explanation:
Measures of centre, mean and median, can be calculated as follows:
First, bear in mind that each dot represents a value in the data set.
==>Mean:
Mean is the sum of all values in the data set divided by the number of data set we have.
The sum can be calculated as follows:
0 (1) = 0
4 (3) = 12
5(8) = 40
6(3) = 18
7(1) = 7
8(5) = 40
9(2) = 18
10 (3) = 30
Sum = 0+12+40+18+7+40+18+30 = 165
No of data set = 26
Mean = 165/26 = 6.346 ≈ 6.3 (nearest tenth place)
==>Median: this is the middle value in the data set. Since the number of data set is even number (26) , the middle value lies between the 13th and 14th data points. The average of the 13th and 14th data points will give us the median value.
Thus, the 13th and 14th values are both 6.
Therefore, median = (6+6) ÷ 2 = 6

Answer:
The mode is 5, because 5 occurs 8 times, which is more than any other numbers occurring more than once. The median is 6, and this is because when you line up the numbers in order and cross them off to find the middle number, it is 6. I rounded to the mean to about 6.4. I got this by adding all of the numbers up, or by doing 12 + 40 +18 +7, etc, and got the total of 165. Because there is a total of 26 data points, I divided those numbers and got 6.3461, which ends up rounding to 6.4.
Step-by-step explanation:
change wording
The measure of ∠BCD is 120°. The measure of ∠ABC is 85°.
What is measure of ∠BAC?
Enter your answer in the box.

Answers
Answer:
35
Step-by-step explanation:
since ACD is a line so angle BCA+angle BCD=180
BCA+120=180
BCA=60
The total degrees of all interior angles of triangle is 180
So angle BAC+BCA+ABC=180,
BAC+60+85=180
BAC=35
We know that BCD is 120° which means that BCA is 60°. (120+60= 180)
We also know that ABC is 85°
So 85° + 60° = 145°
We know a triangle = 180°, so we can subtract the sum of the two prior angles to give us the missing angle BAC
180 - 145 = 35°
For the following parameterized curve, find the unit tangent vector at the given value of t. r(t)=⟨28t,2, t
7
⟩, for −2
(t)=0, there is no tangent vector.
Answers
The unit tangent vector of the parameterized curve r(t) = ⟨28t, 2, t^7⟩ at t = -2 does not exist.
To find the unit tangent vector, we need to differentiate the given vector function r(t) with respect to t. The unit tangent vector is obtained by normalizing the resulting derivative.
The derivative of r(t) with respect to t is:
r'(t) = ⟨28, 0, 7t^6⟩
To find the unit tangent vector at t = -2, we substitute the value into the derivative:
r'(-2) = ⟨28, 0, 7(-2)^6⟩ = ⟨28, 0, 7(64)⟩ = ⟨28, 0, 448⟩
Next, we calculate the magnitude of the tangent vector:
| r'(-2) | = √(28^2 + 0^2 + 448^2) = √(784 + 200704) = √201488 = 449.08
Finally, we divide the derivative vector by its magnitude to obtain the unit tangent vector:
T(-2) = r'(-2) / | r'(-2) | = ⟨28/449.08, 0/449.08, 448/449.08⟩ ≈ ⟨0.0623, 0, 0.9978⟩
At t = -2, the unit tangent vector of the parameterized curve r(t) = ⟨28t, 2, t^7⟩ does not exist. This is because the derivative vector, when normalized, yields a magnitude of 449.08, which is not zero. Thus, we can conclude that there is no unit tangent vector at t = -2.
To know more about tangent vector, visit;
https://brainly.com/question/31584616
#SPJ11
Modeling an Equation
Use the algebra tiles to model the equation
2x + 4 = 3x + (−1). Then complete the sentences.
To model 2x + 4, you need:
positive x-tiles to represent 2x.
positive unit tiles to represent 4.
To model 3x + (−1) you’ll need:
3
x-tiles to represent 3x.
1
unit tile to represent –1.
Answers
The sentences is completed as follows
To model 2x + 4, you need:
2 positive x-tiles to represent 2x4 positive unit tiles to represent 4To model 3x + (−1) you’ll need:
3 positive x-tiles to represent 3x1 negative unit tile to represent –1What is algebra tile models?An algebra tile model is a graphic representation made out of various arrangements of algebra tiles. A model's function is to depict a polynomial expression or equation.
Algebra tiles it self are shapes of different colors that represents numbers or parts of numbers.
In the question, algebra tiles are used to represent the equations used in the problem. The tiles in the problem will be of 3 types
x-tilespositive unit tiles negative unit tiles2x + 4
In this case, the equation will require the twice the x-tiles then 4 positive unit tiles
3x + (−1)
In this case, the problem is represented using 3 x-tiles and 1 negative unit tile.
Learn more about equation modeling here:
https://brainly.com/question/29363429
#SPJ1
Answer:2,4,positive,negative
Step-by-step explanation:

There is a probablity of ____ that any individual at a random from
a population will fall (plus or minus) one standard deviation of
the mean.
Answers
Step-by-step explanation:
I hope this answer is helpful ):

as a review recall the difference between perimeter, area and volume
Answers
Answer:
perimeter are the adding up of all side in a figure. Area is length times width and volume is length x width x height
Step-by-step explanation:
plz mark the brainliest
Answer:
Volume: The amount a container can hold.
Area: The space a flat shape covers.
Perimeter: The length around an object.
Step-by-step explanation:
I'm trying to figure this out but i can't so if you can help that well be much appreciated
;)
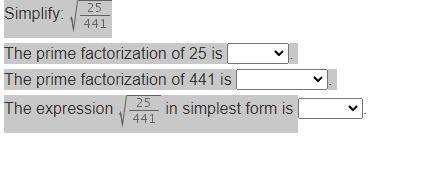
Answers
prime factorization of 25 is 5*5
prime factorization of 441= 3*3*7*7
ANSWER= 5/21
Question is in the attached photo.

Answers
Answer:
#9a)
Parallels of latitudeb)
i)
5 major circles: the Arctic Circle, the Tropic of Cancer, the Equator, the Tropic of Capricorn and the Antarctic Circleii)
One - equator#10Radius of the parallel of latitude 25°N is equal to symmetrical one, which is 25°SYour foot measures 10.8 inches. what proportion can you use to determine how many centimeters, x, it is? :A) 10.8in. 2.54in. xcm 1cm 2.54in. B) 10.8cm xin lcm C) 10.8in lin. хст 2.54cm D) 10.8in 2.54cm XCM lin
Answers
Your foot measure in centimeter is 4.25 centimeters and the proportion is 10.8 inches / 2.54 centimeters = x centimeters.
A proportion is an equation that states that two ratios are equal. It's often used to convert from one unit of measurement to another.
In your case, you want to convert 10.8 inches to centimeters, so you'll use a proportion to help you do that.
Here the correct proportion to use is 10.8 inches / 2.54 centimeters = x centimeters.
In this proportion, the first ratio on the left side of the equation represents 10.8 inches in terms of centimeters, and the second ratio on the right side of the equation represents x centimeters in terms of inches.
Since we know the conversion factor between inches and centimeters, 2.54 centimeters per inch, we can substitute that into the proportion.
=> 10.8 inches / 2.54 centimeters = x centimeters
=> 10.8 inches / 2.54 centimeters
=> 10.8 / 2.54 centimeters = 4.25 centimeters.
Therefore, 10.8 inches is equal to 4.25 centimeters.
To know more about proportion here.
https://brainly.com/question/16937826
#SPJ4
Find the equation of each of the straight lines, given its gradient and the coordinates of a point on the line.
6, (2, 8) 7, (2,10)
Answers
The equation of the straight lines are:
For m = 6 and (x1, y1) = (2, 8) => y = 6x - 4
For m = 7 and (x1, y1) = (2, 10) => y = 7x - 4
We know that the equation of a line with gradient m and y-intercept is:
y = mx + c.
We need to find the equation of each of the straight lines, given its gradient and the coordinates of a point on the line.
We know the point-slope form of equation of line,
(y - y1) = m(x - x1)
For m = 6 and (x1, y1) = (2, 8)
(y - 8) = 6(x - 2)
y - 8 = 6x - 12
y = 6x - 4
For m = 7 and (x1, y1) = (2, 10)
(y - 10) = 7(x - 2)
y - 10 = 7x - 14
y = 7x - 4
Therefore, the equation of the straight lines are:
For m = 6 and (x1, y1) = (2, 8) => y = 6x - 4
For m = 7 and (x1, y1) = (2, 10) => y = 7x - 4
Learn more about equation of line here:
https://brainly.com/question/21511618
#SPJ1
If three consecutive numbers x, x + 1, x + 2 equal to 39, what is the value of x?
1
5
7
12
14
Answers
3x + 3 = 39
3x = 36
X = 3
Classify the trios of sides as acute, obtuse, or right triangles.

Answers
The triangles with the given side lengths are classified as follows:
Acute: 27, 36, 46, \(6, \sqrt{61}, \sqrt{96}\)Right: \(\sqrt{6}, 6, \sqrt{42}\), \(\sqrt{23}, 7, \sqrt{72}\), 7, 24, 25, 15, 20, 25.Obtuse:How to classify the triangles?The ordered side lengths of the triangles are given as follows:
a, b and c.
Considering these side lengths, the triangles are classified as follows:
Acute if a² + b² > c².Right if a² + b² = c².Obtuse if a² + b² < c².More can be learned about triangles at https://brainly.com/question/1058720
#SPJ1
Given secant of theta is equal to the square root of 10 over 2 comma what is cos?
a. one fifth
b. 5
c. square root of 10 over 2
d. square root of 10 over 5
Answers
Answer:
D square root of 10 over 5
Step-by-step explanation:
sec means \(\frac{1}{x}\), so if sec of theta is \(\frac{\sqrt{10} }{2}\) in this situation then you can set those equal to one another to get x.
x=\(\frac{\sqrt{10} }{5}\)
cos is just another way to say x so what you got for x is your answer
The secant of theta is equal to the square root of 10 over 2 comma what is, then the value of cos is square root of 10 over 5 .The correct option is d.
What is secant?For a right angle triangle, secant of the angle formed by the sides opposite to hypotenuse is equal to the ratio of Hypotenuse and the base of triangle,
Given the value of sec of θ
secθ = sqrt (10)/2
Then cos θ = 1/secθ
Plug the value, we get
secθ= sqrt (10) / 5
Thus, the correct option is d.
Learn more about secant.
https://brainly.com/question/23026602
#SPJ1
Systems of equations are often used to model real-life situations. List 2 examples where a system of equations could describe a real-life situation. Elaborate on why you think a system of equations would be useful for each example.
Answers
2 examples where a system of equations could describe a real-life situation are given below.
What is equation?Equation is a physical and mathematical statement that describing physical phenomena and the relationship between different physical quantity typically consist of variable simple presenting physical quantity and then it personal variable may be pointed such as your energy.
1.Modeling a business’s profit: A business can be represented by a system of equations to find the maximum profit. The equations can include the cost of the product, the price of the product, the number of units of the product sold, and other variables such as taxes and shipping costs. By representing the business with a system of equations, a business can optimize the equation to achieve the maximum profit.
2. Modeling the housing market: A system of equations can be used to model the housing market. The equations can include variables such as housing prices, the number of houses on the market, the number of buyers, the supply of housing, and the demand for housing. By using a system of equations, economists can better understand the housing market and make predictions about future trends in the market.
To know more about the equation click-
https://brainly.com/question/26408808
#SPJ1
Evaluate 2.6 raised to the seventh power divided by 2.6 raised to the sixth power, all raised to the second power.
Answers
The evaluation of 2.6 raised to the seventh power divided by 2.6 raised to the sixth power, all raised to the second power is as follows:
\((\frac{2.6^{7} }{2.6^{6} } )^{2} = 6.76\)
How to evaluate an expression?2.6 raised to the seventh power divided by 2.6 raised to the sixth power, all raised to the second power.
The following expression can be evaluated as follows;
\((\frac{2.6^{7} }{2.6^{6} } )^{2}\)
Using the law of indices,
\((A^{x} )^{y} = A^{xy}\)
Therefore,
\((\frac{2.6^{7} }{2.6^{6} } )^{2} = (\frac{2.6^{14} }{2.6^{12} } )\)
Using the law of indices,
\(\frac{A^{x} }{B^{y} } = A^{x-y}\)
Hence,
\((\frac{2.6^{7} }{2.6^{6} } )^{2} = (\frac{2.6^{14} }{2.6^{12} } ) = 2.6^{14-12} = 2.6^{2} = 6.76\)
Therefore,
\((\frac{2.6^{7} }{2.6^{6} } )^{2} = 6.76\)
The evaluation of 2.6 raised to the seventh power divided by 2.6 raised to the sixth power, all raised to the second power is 6.76.
learn more on expression here: https://brainly.com/question/28337613
#SPJ1
Answer: A
Step-by-step explanation:
i got it right
The distribution of the amount of money spent on book purchases for a semester by college students has a mean of $300 and a standard deviatin of $50.
Assuming no information concerning the shape of the distribution is known, what percentage of the students spent between $200 and $400?
a) at least 95%
b) approximately 95%
c) approximately 68%
d) at least 75%
Answers
The correct option for this question is c) approximately 68% of the students spent between $200 and $400.
Step 1: Identify the given information. The mean is $300, and the standard deviation is $50. The range is between $200 and $400.
Step 2: Calculate the number of standard deviations between the mean and each boundary. For $200, it's ($200 - $300) / $50 = -2 standard deviations. For $400, it's ($400 - $300) / $50 = 2 standard deviations.
Step 3: Since we don't have information about the shape of the distribution, we will use the Empirical Rule, which states that for a normal distribution, approximately 68% of the data falls within 1 standard deviation, 95% within 2 standard deviations, and 99.7% within 3 standard deviations of the mean.
Step 4: In this case, we are looking at 2 standard deviations from the mean (between $200 and $400). According to the Empirical Rule, approximately 95% of the data falls within this range. However, since we don't know the exact shape of the distribution, we can't say for certain that 95% of the students spent between $200 and $400. However, we do know that at least 68% of the students would fall within 1 standard deviation of the mean. Thus, we can conclude that approximately 68% of the students spent between $200 and $400.
To know more about standard deviation visit:
brainly.com/question/23907081
#SPJ11
The lengths of two similar figures are 32 ft and 36 ft. What is the scale factor, perimeter ratio and area ratio in simplest form of the first to the second.
Answers
Scale factor from the first to the second figure is 9/8, Perimeter ratio is 37/32 and the area ratio of the first to the second figure is 81/64 in simplest form.
Since the figures are similar, their corresponding sides are proportional. Let the scale factor between the two figures be x, then we have:
x = (length of the second figure) / (length of the first figure)
= 36/32 = 9/8
So the scale factor from the first to the second figure is 9/8.
Perimeter ratio = (perimeter of the second figure) / (perimeter of the first figure)
Perimeter ratio = (9/8) × [(36 + 32) / 2] / 32 = 37/32
Since the area of a figure is proportional to the square of its sides, and the sides are proportional by the scale factor
The area of the second figure is (9/8)² times the area of the first figure.
Area ratio = (area of the second figure) / (area of the first figure)
= [(9/8)² × (area of the first figure)] / (area of the first figure)
Area ratio = 81/64
Hence, scale factor from the first to the second figure is 9/8, Perimeter ratio is 37/32 and the area ratio of the first to the second figure is 81/64 in simplest form.
To learn more on Ratios click:
https://brainly.com/question/1504221
#SPJ1
What’s the answer pls help

Answers
Answer:
m= - 3/2
c=1/2
Step-by-step explanation:
y=mx+c (formula for finding slope)
y= -3x/2+1/2
m= - 3/2
c=1/2
