Answers
Answer: yes
Step-by-step explanation: there’s a pattern of 2, as we can see from the first equation. 5+2 is 7, so therefore the answer is yes.
Related Questions
??? Need help please

Answers
Explanation
Take points
(4,3) and (6,-3)
-3-(3)
———= -6/2 which equals -3
6-4
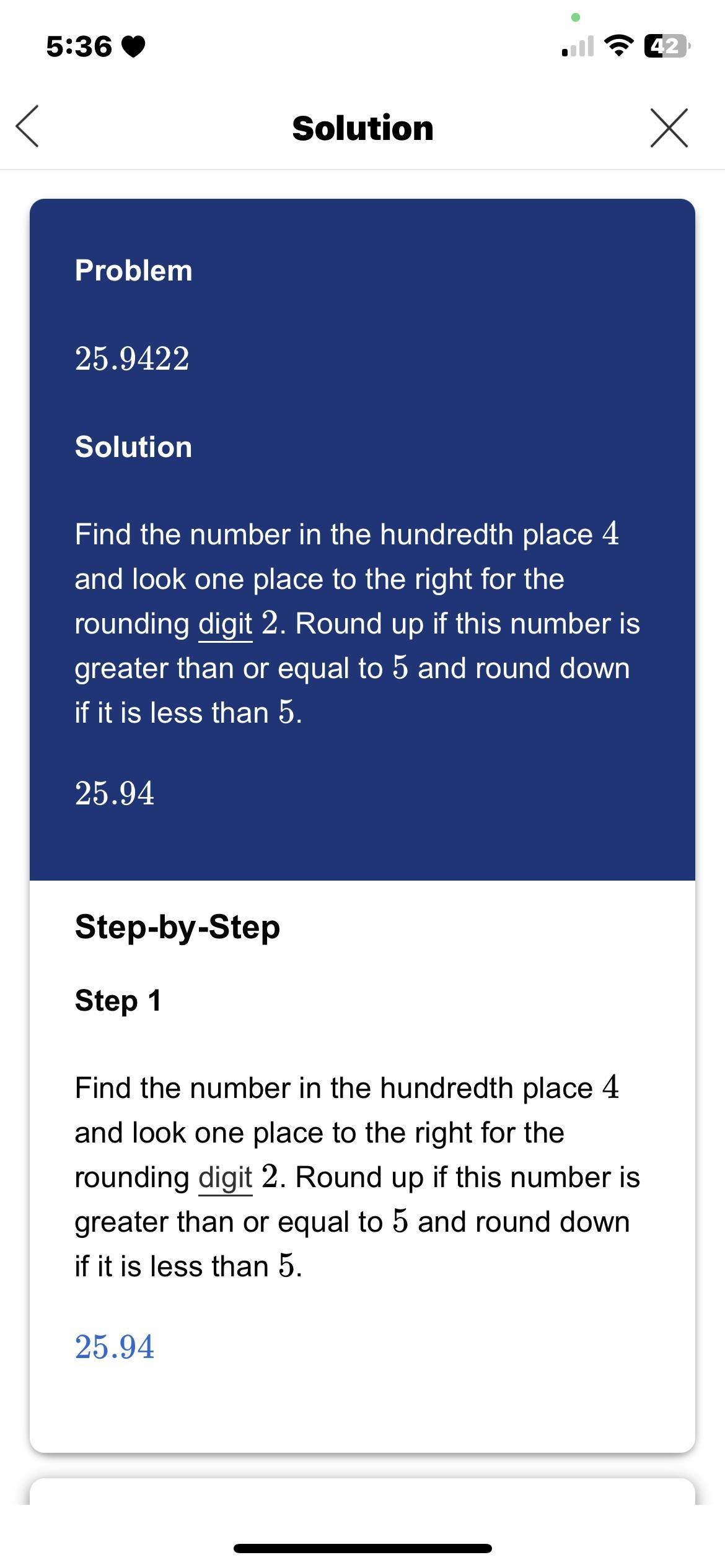
what is 25.9422 rounded to the nearest hundredth
Answers
Answer:
25.9422 rounded to the nearest hundredth is 25.94.
Answer:
Step-by-step explanation:
the standard iq test has a mean of 96 and a standard deviation of 14. we want to be 90% certain that we are within 4 iq points of the true mean. determine the required sample size.
Answers
The required sample size is determined by finding the z-score that corresponds to a 90% confidence interval and then using that z-score to calculate the sample size. In this case, the z-score is 2.24 and the sample size is 467.
In order to determine the required sample size to be 90% certain that we are within 4 IQ points of the true mean, we must first calculate the z-score that corresponds to a 90% confidence interval. This z-score is calculated by subtracting the lower bound of the interval from the mean, and then dividing this difference by the standard deviation. In this case, the z-score is 2.24. We then use this z-score to calculate the required sample size, which is calculated by taking the z-score, squaring it, and then multiplying it by the sample variance. In this case, the sample size is 467. This means that we need at least 467 samples in order to be 90% certain that we are within 4 IQ points of the true mean.
Learn more about sample size here
https://brainly.com/question/25894237
#SPJ4
Sheldon also picks tomatoes from his garden. He picked 4 4/10 but 1.5 were rotten and had to be thrown away. How many kilograms of tomatoes were not rotten? Write an equation that shows how you reached your answer.
Answers
Given:
Number of tomatoes Sheldon picks = \(4\dfrac{4}{10}\) kg
Rotten tomatoes = 1.5 kg
To find:
How many kilograms of tomatoes were not rotten?
Solution:
Number of tomatoes Sheldon picks = \(4\dfrac{4}{10}\) kg
= \(\dfrac{4(10)+4}{10}\) kg
= \(\dfrac{40+4}{10}\) kg
= \(\dfrac{44}{10}\) kg
= \(4.4\) kg
Rotten tomatoes = 1.5 kg
Remaining tomatoes which are not rotten is
Required tomatoes = Tomatoes Sheldon picks - Rotten tomatoes
= \(4.4-1.5\)
= \(2.9\) kg
Therefore, the tomatoes which were not rotten is 2.9 kg.
Tony has 75 dollars to spend on a game controller that costs $35 and used video games
costing 8 dollars each. How many video games can he buy?
Answers
Answer:5 I think
Step-by-step explanation:
75-35=40 40 divided by 8 is 5
Answer:
The answer is 5=x (he is able to buy 5 videogames)
Step-by-step explanation:
First, you need to put this into an equation format with a variable (x) for the videogames. Here is what the equation should look like: 75 = 35 + 8x
75 being the total amount of money he has to spend, 35 being what he had to spend or knows he will spend on the controller, and the 8 is for each videogame. We put an 'x' behind the 8 to signal that we don't know how many games he can buy. So, then we need to solve the equation.
75=35+8x
-35 on both sides
So, 40=8x, then you divide by 8 to get x by itself
5=x
The 'x' in this equation is how many videogames he is able to buy. The way you could check your work is if you plugged 5 back into x. What I mean is this: 35+8(5) needs to equal 75, and it does, so you're good!
4. Evaluate cos 4π/3
____
Identify the function. a. sine b. cosine c. tangent
d. secant
e. cosecant
f. cotangent Identify the argument of the function. ______
Identify the function value. ______
Answers
The function is cosine. The argument of the function is 4π/3. The function value is -0.5.
The cosine function is a periodic function that has a period of 2π. This means that the value of the cosine function repeats every 2π radians. The argument of the cosine function is the angle in radians.
When the argument of the cosine function is 4π/3, the value of the function is -0.5. This can be found using the unit circle. The unit circle is a circle with radius 1. The cosine of an angle is the x-coordinate of the point on the unit circle that is radians counterclockwise from the positive x-axis.
When the angle is 4π/3, the point on the unit circle is (-0.5, 0.866). This means that the cosine of 4π/3 is -0.5.
Therefore, the answer to the question is:
Function: cosine
Argument: 4π/3
Function value: -0.5
Learn more about cosine here : brainly.com/question/28355770
#SPJ11
use graphing the solve the systems of equations? x^2+6x+8 and x+4
Answers
The solution of the given system of equations is (-2, -4).
The given system of equations is:x² + 6x + 8 = 0x + 4 = 0To solve the system using graphing, follow the given steps below:Step 1: Graph both the equations on the same coordinate axes. For this, rewrite the given quadratic equation as y = x² + 6x + 8. Then, draw the graphs of y = x² + 6x + 8 and y = -4 on the same coordinate plane. The graphs of both equations intersect at x = -2. Therefore, the solution of the system is (-2, -4).
The graph of y = x² + 6x + 8 is given below: The graph of y = -4 is a straight horizontal line passing through the point (-4, 0).The graph of both the equations on the same coordinate axes is given below: Step 2: Identify the point of intersection of the graphs. The point of intersection of the graphs is the solution of the system. Therefore, the solution of the system is (-2, -4).
For more such questions on equations
https://brainly.com/question/29174899
#SPJ8
Choose h and k such that the system has (a) no solution, (b) a unique solution, and (c) many solutions. Give separate answers for each part.
1) x1+ℎx^2=2,4x1+8x2=k
2) x1+3x2= 2, 3x1+hx2= k
Answers
The chosen values are:
a) h = 2 (no solution), any k
b) h ≠ 2 (unique solution), any k
c) h = 2 (many solutions), k = 16
To determine values of h and k that result in different solution scenarios for the given systems of equations, we can analyze the coefficient matrices and their determinants.
System 1:
x1 + h*x2 = 2
4x1 + 8x2 = k
a) For the system to have no solution, the coefficient matrix's determinant must be zero, while the augmented matrix's determinant is nonzero.
Taking the determinant of the coefficient matrix, we have:
| 1 h |
| 4 8 |
Determinant = (1 * 8) - (4 * h)
= 8 - 4h
For the system to have no solution, the determinant 8 - 4h must be zero. So we solve:
8 - 4h = 0
h = 2
Therefore, for no solution, h = 2. We can choose any value for k.
b) For the system to have a unique solution, the coefficient matrix's determinant must be nonzero.
So we need to ensure that 8 - 4h ≠ 0.
Choosing h ≠ 2 will satisfy this condition. We can choose any value for k.
c) For the system to have many solutions, the coefficient matrix's determinant must be zero, and the augmented matrix's determinant must also be zero.
For this case, we can choose h = 2 (as determined in part a), and k such that the augmented determinant is also zero.
For example, we can choose k = 16, which satisfies the equation 4 * 2 - 8 * 16 = 0.
Therefore, the chosen values are:
a) h = 2 (no solution), any k
b) h ≠ 2 (unique solution), any k
c) h = 2 (many solutions), k = 16
Learn more about Coefficient Matrix at
brainly.com/question/28436712
#SPJ4
Evaluate the following expressions. a. 25/3 b. 20−12/4∗2 c. 32%7 d. 3−5%7 e. 18.0/4 f. 28−5/2.0 g. 17+5%2−3 h. 15.0+3.0∗2.0/5.0
Answers
This expression represents the division of 25 by 3.
a. 25/3 = 8.333...
b. 20 - 12/4 * 2 = 14
c. 32 % 7 = 4
d. 3 - 5 % 7 = -2
e. 18.0/4 = 4.5
f. 28 - 5/2.0 = 25.5
g. 17 + 5 % 2 - 3 = 15
h. 15.0 + 3.0 * 2.0 / 5.0 = 16.2
a. 25/3:
This expression represents the division of 25 by 3.
25/3 = 8.333...
b. 20 - 12/4 * 2:
Following the order of operations (parentheses, exponents, multiplication/division from left to right, and addition/subtraction from left to right):
12/4 = 3
3 * 2 = 6
20 - 6 = 14
c. 32%7:
The % symbol represents the modulo operation (remainder after division).
32 % 7 = 4
d. 3 - 5%7:
Following the order of operations:
5 % 7 = 5 (since 5 divided by 7 leaves a remainder of 5)
3 - 5 = -2
e. 18.0/4:
This expression represents the division of 18.0 by 4.
18.0/4 = 4.5
f. 28 - 5/2.0:
Following the order of operations:
5/2.0 = 2.5 (division with floating-point numbers)
28 - 2.5 = 25.5
g. 17 + 5%2 - 3:
Following the order of operations:
5 % 2 = 1 (since 5 divided by 2 leaves a remainder of 1)
17 + 1 - 3 = 15
h. 15.0 + 3.0 * 2.0/5.0:
Following the order of operations:
3.0 * 2.0 = 6.0
6.0 / 5.0 = 1.2
15.0 + 1.2 = 16.2
To know more about modulo operation, visit:
https://brainly.com/question/30264682
#SPJ11
20 grams is the same as: a. 2000 mg b. 20000 mg c. 200000 mg d. 200 mg
Answers
Answer:
20 grams is the same as option (a) 2000 mg.
Step-by-step explanation:
To convert grams to milligrams, you multiply the value in grams by 1000 because there are 1000 milligrams in one gram. Therefore, 20 grams is equal to 20 * 1000 = 2000 milligrams.
20 grams is equal to 20000 mg.
Explanation:20 grams is equivalent to 20000 mg. To convert grams to milligrams, you need to multiply the number of grams by 1000 since there are 1000 milligrams in one gram. So, 20 grams multiplied by 1000 equals 20000 milligrams.
This question is regarding the conversion of grams (a metric unit of weight) to milligrams. 1 gram is equivalent to 1000 milligrams. Therefore, to convert 20 grams to milligrams, you would multiply 20 (the number of grams) by 1000 (the number of milligrams in 1 gram).
20 grams * 1000 = 20000 milligrams
So, 20 grams is the same as 20000 milligrams, which means the correct answer to your question is b. 20000 mg.
Learn more about Converting grams to milligrams here:https://brainly.com/question/37937829
#SPJ11
Evaluate limx→1 x1000−1/x−1. Calculate the differentiation dy/dx of tan(x/y)=x+6
Answers
The differentiation dy/dx of tan(x/y) = x + 6 is given by (tan(x/y) - 6 * (dy/dx)) / (1 - (x/y) * (sec^2(x/y) * (1/y))).
To evaluate the limit limx→1 \((x^1000 - 1)\)/ (x - 1), we can notice that the expression \(x^1000\) - 1 can be factored using the difference of squares formula: \(a^2 - b^2 = (a - b)(a + b).\)
So we have:
limx→1 \((x^1000 - 1) / (x - 1)\)
= limx→1 \([(x^500 - 1)(x^500 + 1)] / (x - 1)\)
Now, we can cancel out the common factor of (x - 1) in the numerator and denominator:
= limx→1 (x^500 + 1)
Substituting x = 1 into the expression, we get:
= 1^500 + 1
= 1 + 1
= 2
Therefore, the limit limx→1 (x^1000 - 1) / (x - 1) is equal to 2.
Regarding the differentiation dy/dx of tan(x/y) = x + 6, we need to use the quotient rule to differentiate implicitly.
First, let's rewrite the equation as y = x * tan(x/y) - 6y.
Differentiating implicitly, we have:
dy/dx = (d/dx)[x * tan(x/y)] - (d/dx)[6y]
Using the quotient rule on the first term:
(d/dx)[x * tan(x/y)] = tan(x/y) + x * (d/dx)[tan(x/y)]
To differentiate the tangent function, we use the chain rule:
(d/dx)[tan(x/y)] = sec^2(x/y) * (d/dx)[x/y]
= sec^2(x/y) * (1/y) * dy/dx
Substituting these derivatives back into the equation, we have:
dy/dx = tan(x/y) + x * (sec^2(x/y) * (1/y) * dy/dx) - (d/dx)[6y]
Now, let's solve for dy/dx by isolating the term:
dy/dx - (x/y) * (sec^2(x/y) * (1/y) * dy/dx) = tan(x/y) - (d/dx)[6y]
Factor out dy/dx:
dy/dx * (1 - (x/y) * (sec^2(x/y) * (1/y))) = tan(x/y) - (d/dx)[6y]
Combine the derivative of y with respect to x:
dy/dx * (1 - (x/y) * (sec^2(x/y) * (1/y))) = tan(x/y) - 6 * (dy/dx)
Multiply through by (y / (y - x * sec^2(x/y))):
dy/dx * (y / (y - x * sec^2(x/y))) * (1 - (x/y) * (sec^2(x/y) * (1/y))) = (tan(x/y) - 6 * (dy/dx)) * (y / (y - x * sec^2(x/y)))
Simplifying the equation:
dy/dx = (tan(x/y) - 6 * (dy/dx)) * (y / (y - x * sec^2(x/y))) / (y / (y - x * sec^2(x/y))) * (1 - (x/y) * (sec^2(x/y) * (1/y)))
dy/dx = (tan(x/y) - 6 * (dy/dx)) / (1 - (x/y) * (sec^2(x/y) * (1/y)))
Therefore, the differentiation dy/dx of tan(x/y) = x + 6 is given by (tan(x/y) - 6 * (dy/dx)) / (1 - (x/y) * (sec^2(x/y) * (1/y))).
Learn more about limit here:
https://brainly.com/question/30339394
#SPJ11
Translate this phrase into an algebraic expression 66 decreased by twice Carlos's savings Use the variable c to represent Carlos's savings.
Answers
This is the answer to your question
Nicole measured some distances on a map of Lassen Volcanic National Park. The scale on the map is 34
inch = 2 miles. What is the actual distance from Raker Peak to Hat Mtn?
Responses
A 4 miles4 miles
B 223
miles2 2 3 miles
C 214
miles2 1 4 miles
D 212
miles2 1 2 miles
E 3 miles
Answers
Performing a change of scale we will see that the actual distance is 4 miles.
What is the actual distance from Raker Peak to Hat Mtn?We know that the scale is:
3/4 inch = 2 miles.
And the distance that Nicole found on the map is (1 + 1/2) inches.
We can rewrrite the scale as:
1 inch = (4/3)*2 miles
1 inch = (8/3) miles.
Then the actual distance will be:
distance = (1 + 1/2) inches = (1 + 1/2)*(8/3) miles = 4 miles.
The correct option is A.
Learn more about changes of scale:
https://brainly.com/question/15891755
#SPJ1
Match the stem and leaf plot
to the correct set of data.
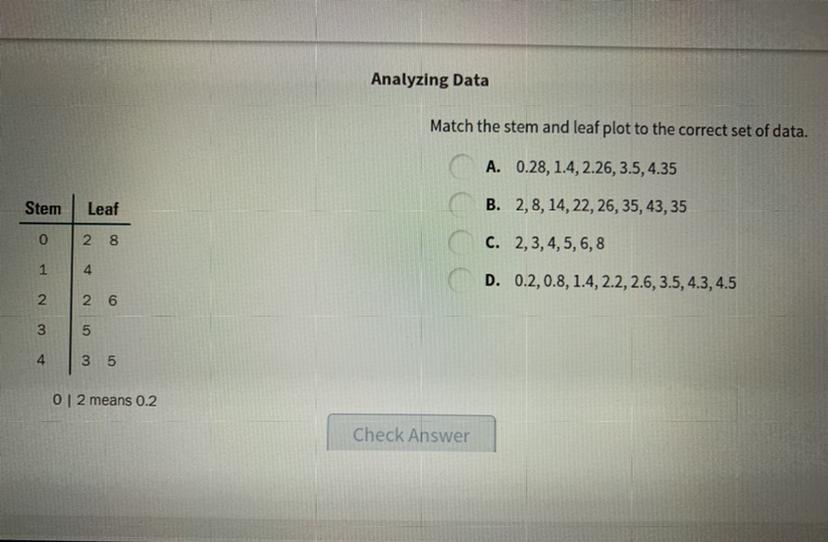
Answers
24. Vince spent half of the money in his wallet on a new jumper
He then spent S15 on lunch.
After lunch he spent two thirds of the money remaining in his wallet on a hat.
If he is left with SIO in his wallet. how much did he have to begin with?
Answers
Answer:
$90
Step-by-step explanation:
Sorry to ask but can I have brainliest
how many different subsets of 5 students we can select from a classroom of 20?
Answers
There are 2002 different subsets of 5 students that can be selected from a classroom of 20. To calculate this, you can use the binomial coefficient formula.
The binomial coefficient is equal to nCr, where n is the total number of objects (in this case 20 students) and r is the number of objects you want to select (in this case 5 students).
Using the binomial coefficient, we can calculate that there are 20C5 = 2002 different subsets of 5 students that can be selected from a classroom of 20.
nCr = 20C5
20C5 = 20! / ((20-5)! 5!)
20! = 20 x 19 x 18 x 17 x 16 x 15 x 14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
5! = 5 x 4 x 3 x 2 x 1
20C5 = 20 x 19 x 18 x 17 x 16 x 15 x 14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 / (5 x 4 x 3 x 2 x 1 x 15 x 14 x 13 x 12 x 11) = 2002
Therefore, there are 2002 different subsets of 5 students that can be selected from a classroom of 20.
To learn more about binomial coefficient:
https://brainly.com/question/29149191#
#SPJ11
6. Compute the residue of the function at each singularity. a) \( z^{2} \sin \frac{1}{z} \) b) \( \frac{\sinh z}{\cosh z} \)
Answers
The residue of function \(\(f(z) = z^2 \sin\left(\frac{1}{z}\right)\)\) at singularity z = 0 is 1 and the function \(\(f(z) = \frac{\sinh z}{\cosh z}\)\) has no residue at the singularities \(\(z = (2n+1)\frac{\pi}{2}i\)\) where \(\(\cosh z = 0\)\).
a) To compute the residue of the function \(\(f(z) = z^2 \sin\left(\frac{1}{z}\right)\)\) at the singularity z = 0, we can use the Laurent series expansion of the function around that point.
The Laurent series expansion of \(\(\sin\left(\frac{1}{z}\right)\)\) can be written as:
\(\[\sin\left(\frac{1}{z}\right) = \sum_{n=0}^{\infty} (-1)^n \frac{1}{(2n+1)!}\frac{1}{z^{2n+1}}\]\)
Multiplying this series by z², we have:
\(\(z^2 \sin\left(\frac{1}{z}\right) = \sum_{n=0}^{\infty} (-1)^n \frac{1}{(2n+1)!}\frac{1}{z^{2n-1}}\)\)
Now, we can see that the coefficient of \(\(\frac{1}{z}\)\) in this series is 0, and the coefficient of \(\(\frac{1}{z^2}\)\) is 1.
Thus, the residue of (f(z)) at (z = 0) is 1.
b) To compute the residue of the function \(\(f(z) = \frac{\sinh z}{\cosh z}\)\) at the singularities, we need to identify the singular points of the function.
The function (cosh z) has a singularity when (cosh z = 0), which occurs at \(\(z = (2n+1)\frac{\pi}{2}i\)\) for \(\(n \in \mathbb{Z}\)\).
At these singularities, the denominator becomes zero, and we need to examine the behavior of the function to compute the residues.
Considering the limit of (f(z)) as (z) approaches each singularity, we can evaluate:
\(\[\lim_{{z \to (2n+1)\frac{\pi}{2}i}} f(z) = \frac{\sinh((2n+1)\frac{\pi}{2}i)}{\cosh((2n+1)\frac{\pi}{2}i)}\]\)
Now, we know that \(\(\sinh(z) = \frac{1}{2}(e^z - e^{-z})\)\) and
Substituting these expressions into the limit, we have:
\(\[\lim_{{z \to (2n+1)\frac{\pi}{2}i}} f(z) = \frac{\frac{1}{2}(e^{(2n+1)\frac{\pi}{2}i} - e^{-(2n+1)\frac{\pi}{2}i})}{\frac{1}{2}(e^{(2n+1)\frac{\pi}{2}i} + e^{-(2n+1)\frac{\pi}{2}i})}\]\)
The numerator can be written as:
\(\[\frac{1}{2}(e^{(2n+1)\frac{\pi}{2}i} - e^{-(2n+1)\frac{\pi}{2}i}) = \frac{1}{2}(i^{2n+1} - (-i)^{2n+1}) = \frac{1}{2}(i - (-i)) = i\]\)
The denominator can be written as:
\(\[\frac{1}{2}(e^{(2n+1)\frac{\pi}{2}i} + e^{-(2n+1)\frac{\pi}{2}i}) = \frac{1}{2}(i^{2n+1} + (-i)^{2n+1}) = \frac{1}{2}(i + (-i)) = 0\]\)
Therefore, we have a removable singularity at \(\(z = (2n+1)\frac{\pi}{2}i\)\) because the numerator is nonzero and the denominator is zero.
At these singularities, the function can be extended analytically, and there is no residue.
To know more about residue of function refer here:
https://brainly.com/question/33106783#
#SPJ11
introduction paragraph about Peter G. L. Dirichlet
Answers
Answer:
Johann Peter Gustav Lejeune Dirichlet (German: [ləˈʒœn diʀiˈkleː]; 13 February 1805 – 5 May 1859) was a German mathematician who made contributions to number theory (including creating the field of analytic number theory), and to the theory of Fourier series and other topics in mathematical analysis
Write a formula for the given measure. Tell what each variable represents. Identify which variable depends on which in the formula.
1. The perimeter of a rectangle with the length of 4 meters.
2. The area of a triangle with a base length of 10 feet.
Answers
find the derivatives of the following implicit function

Answers
Answer:
\(\frac{d}{dx}\left(y\right)=\frac{2-6x+6y}{-6x+2y+1}\)
Step-by-step explanation:
\(3x^2-6xy+y^2=2x-y\\\mathrm{Treat\:}y\mathrm{\:as\:}y\left(x\right)\\\mathrm{Differentiate\:both\:sides\:of\:the\:equation\:with\:respect\:to\:}x\\\frac{d}{dx}\left(3x^2-6xy+y^2\right)=\frac{d}{dx}\left(2x-y\right)\\\frac{d}{dx}\left(3x^2-6xy+y^2\right)=6x-6\left(y+x\frac{d}{dx}\left(y\right)\right)+2y\frac{d}{dx}\left(y\right)\\\frac{d}{dx}\left(2x-y\right)=2-\frac{d}{dx}\left(y\right)\\6x-6\left(y+x\frac{d}{dx}\left(y\right)\right)+2y\frac{d}{dx}\left(y\right)=2-\frac{d}{dx}\left(y\right)\)
\(\mathrm{For\:convenience,\:write\:}\frac{d}{dx}\left(y\right)\mathrm{\:as\:}y^{'\:}\\6x-6\left(y+xy^{'\:}\right)+2yy^{'\:}=2-y^{'\:}\\\mathrm{Isolate}\:y^{'\:}:\quad y^{'\:}=\frac{2-6x+6y}{-6x+2y+1}\\y^{'\:}=\frac{2-6x+6y}{-6x+2y+1}\\\mathrm{Write}\:y^{'\:}\:\mathrm{as}\:\frac{d}{dx}\left(y\right)\\\frac{d}{dx}\left(y\right)=\frac{2-6x+6y}{-6x+2y+1}\)
Two cars travel at the same speed to different destinations. Car A reaches its destination in 12 minutes. Car B reaches its destination in 18 minutes. Car B travels 4 miles farther than Car A. How fast do the cars travel? Write your answer as a fraction in simplest form.
Answers
Answer:
chatGPT
Step-by-step explanation:
Let's denote the speed of each car as v, and the distance that Car A travels as d. Then we can set up two equations based on the information given:
d = v * (12/60) (since Car A reaches its destination in 12 minutes)
d + 4 = v * (18/60) (since Car B travels 4 miles farther than Car A and reaches its destination in 18 minutes)
Simplifying the equations by multiplying both sides by 60 (to convert the minutes to hours) and canceling out v, we get:
12v = 60d
18v = 60d + 240
Subtracting the first equation from the second, we get:
6v = 240
Therefore:
v = 240/6 = 40
So the cars travel at a speed of 40 miles per hour.
Mrs. Fisher worked her 40 regular hours last week, plus 4 overtime hours at the double-time rate. Her gross pay was $576. What was her hourly rate?
Answers
Answer: $12.
Step-by-step explanation:
4 overtime hours at the double-time rate =
4*2=8 regular hours.
Hence,
Mrs. Fisher worked her 40+8 regular hours last week.
Mrs. Fisher worked her 48 regular hours last week.
Her gross pay was $576.
So,
$576:48=
$12.
Theophylline is a pharmaceutical drug that is sometimes used to help with lung function. You observe a case where the lab results indicate that a sample of theophylline (initial concentration of 2.0 x 10-3 M) has been metabolized to a concentration of 1.0 x 10-3 M in 24 hours. In another 24 hours the drug concentration was 5.0 x 10-4 M. What is the rate of decomposition four (4) hours after the initial sample was taken
Answers
The fifth partial sum represents the sum of the first 5 terms in the sequence is equal to 2210.
The fifth partial sum represents the sum of the first 5 terms in the sequence.
What is the partial sum of sequence?
The partial sum of a sequence gives the sum of the first n terms in the sequence.
Thus, the fifth partial sum represents the sum of the first 5 terms in the sequence.
The given geometric sequence :
$400, $420, $441, $463, and $486.
The fifth partial sum of the above sequence will be :
$400+ $420+ $441+$463+$486=$2210
Therefore, the fifth partial sum represents the sum of the first 5 terms in the sequence equal to 2210.
To learn more about the sequence visit:
brainly.com/question/7882626
The rate of decomposition as per half life is 0.0000545 M.
what is half life?
A quantity's half-life t(1/2) is the amount of time needed for it to decrease to half of its initial value. In nuclear physics, the phrase is frequently used to indicate how rapidly unstable atoms decay radioactively or how long stable atoms last. The phrase is also used more broadly to describe any kind of exponential decay (or, very infrequently, nonexponential decay). The biological half-life of medications and other compounds in the human body, for instance, is a term used in the medical sciences. Half-opposite life's in exponential growth is time's doubling.Drug concentration decreases from 0.002M to 0.001M in 24 hours.
Again, Drug concentration decreases from 0.001M to 0.0005 M in subsequent 24 hours.
Therefore, t(1/2) = 24 hours
K= 0.693/t(1/2) = 0.693/24 = 0.028775 per hour.
K= 2.303/t Log (No/Nt)
Log(No/Nt) =Kt/2.303 =0.05015
No/Nt= Antilog (0.05015) = 1.1224
Nt= No/1.1224 = (0.0017818 M
Rate of decomposition as per half life is calculated as
(No-Nt)/t = 0.0000545 M
Learn more about half- life here:
https://brainly.com/question/11152793
#SPJ4
A recipe for vegetable fritata calls for 10 chard leaves for evry 6 eggs. Eggs are available either by the dozen for $3. 20 or by the half-dozen for $1. 70. Marissa wants to use 25 chard leaves to make a fritata. What is the minimum she should spend on eggs to use all of her chard leaves while keeping the recipe in the correct proportion
Answers
The minimum Marissa should spend on eggs to use all of her chard leaves while keeping the recipe in the correct proportion is $3.40.
To use 10 chard leaves, the recipe calls for 6 eggs. Let's find out how many eggs we need to use 25 chard leaves in the same proportion:
10 chard leaves / 6 eggs = 25 chard leaves / x eggs
where x is the number of eggs needed.
Cross-multiplying, we get:
10 chard leaves * x eggs = 6 eggs * 25 chard leaves
Simplifying, we get:
x = (6 eggs * 25 chard leaves) / 10 chard leaves
x = 15 eggs
So, Marissa needs 15 eggs to use 25 chard leaves in the recipe.
Now, let's find out the cheapest way to buy 15 eggs. She can buy either a dozen eggs for $3.20 or a half-dozen eggs for $1.70. Since a dozen contains 12 eggs and a half-dozen contains 6 eggs, she can either buy:
1 dozen + 3 individual eggs = 15 eggs for $3.20 + $0.24 = $3.44
2 half-dozens = 12 eggs for $3.40
Therefore, the minimum Marissa should spend on eggs to use all of her chard leaves while keeping the recipe in the correct proportion is $3.40.
For more such questions on Equation: brainly.com/question/29657992
#SPJ4
what is the area of the opening in a duct that has a diameter of 7 inches? round the answer to the nearer thousandth square inch.
Answers
The opening area for a 7 inch diameter channel is approximately 38.484 square inches.
The area of a circular opening can be found using the circle area formula given by \(A = \pi r^2\). where A is the area and r is the radius of the circle. In this case, the duct diameter is 7 inches. The radius can be calculated by dividing the diameter by 2, so the radius is 7/2 = 3.5 inches.
Substituting the radius into the equation gives A = π(3,5)^2. Evaluating this formula gives A = \(\pi\)(12.25) ≈ 38.484 square inches. Rounding the result to the nearest thousandth, the area of the channel opening is approximately 38.484 square inches.
Therefore, a 7 inch diameter duct has an orifice area of approximately 38.484 square inches.
Learn more about diameter here:
https://brainly.com/question/31445584
#SPJ11
Pre-image ABCD is dilated to be image A′B′C′D′ . The origin is the center of dilation. What scale factor is used to create the dilation?
Enter your answer in the box.

Answers
Answer:
Times 3
Step-by-step explanation:
John took a 5 1/2 mile walk to his friend's house. He left at 11 a.M. And arrived at his friend's house at 12:45 p.M. Therefore it took him 1 3/4 hours to get to his friends house. If the return trip took 2 1/4 hours, what is the average speed on the return trip?
Answers
Answer:
The average speed on the return trip is 2.44 miles/h.
Step-by-step explanation:
To find the average speed we need to use the following equation:
\( \overline{v} = \frac{d}{t} \)
Where:
d: is the distance
t: is the time
Since the question is to find the average speed on the return trip, we will take the data of the time and speed of only the return trip.
\(\overline{v} = \frac{d}{t} = \frac{5 + 1/2}{2 + 1/4} = 2.44 miles/h\)
Therefore, the average speed on the return trip is 2.44 miles/h.
I hope it helps you!
What was the primary cause of the great famine of 1315â€""1322? regional warfare disrupting agriculture an unprecedented series of locust swarms prolonged rainfall killing crops through flooding an extraordinary period of warmth
Answers
The rains were especially damaging to Europe's food supply, rotting crops and spreading infections that affected cattle. The absence of a stable and adequate food supply resulted in starvation, which was the principal cause of said Great Famine of 1315-1322.
The bulk of Europe witnessed significant crop failure in 1314 and 1315. Before this, there had been a period of rapid population growth caused by agricultural development, which resulted in famine for a significant number of people. Around 5-12% of Northern Europe's population died from famine or accompanying illness.
Famine triggered class conflict and political unrest, destabilizing entire areas. Grain, wheat, grain, oats, bread, and salt were so expensive that many people also couldn't afford them even when they were available. To feed themselves, some abandoned their children and stole from and murdered others.
Learn more about the great famine of 1315 - 1322 at
https://brainly.com/question/9197728?referrer=searchResults
#SPJ4
The question is -
What was the primary cause of the great famine of 1315 - 1322? regional warfare disrupting agriculture an unprecedented series of locust swarms prolonged rainfall killing crops through flooding an extraordinary period of warmth.
Answer: It's option C, prolonged rainfall killing crops throughout flooding
Step-by-step explanation:
A rectangular piece of land measures 20 feet by 15 feet. James created a cement sidewalk, x feet wide, to border a rectangular garden on all four sides as shown below.
If the garden has an area of 150 square feet, how wide is the sidewalk?
A
12.25 feet
B
6.12 feet
C
5 feet
D
2.5 feet

Answers
Answer:
The second and fourth answer are correct
Step-by-step explanation:
The width of the sidewalk if A rectangular piece of land measures 20 feet by 15 feet, James created a cement sidewalk, x feet wide, is 12.25 so, option A is correct.
What is the area?An object's area is how much space it takes up in two dimensions. It is the measurement of the number of unit squares that completely cover the surface of a closed figure.
Given:
A rectangular piece of land measures 20 feet by 15 feet, James created a cement sidewalk, x feet wide,
the garden has an area of 150 square feet,
Calculate the width of the sidewalk as shown below,
Area of rectangular piece = area of garden + area of sidewalk
20 × 15 = 150 + x × x
300 = 150 + x²
x² = 300 - 150
x = √150
x = 12.25
Thus, the width of the sidewalk is 12.25 feet.
To know more about Area:
brainly.com/question/27683633
#SPJ2
It cost sean 3.75 to play 45 songs on an old jukebox. The jukebox only accepts quarters. How many songs can the jukebox play per quarter
Answers
Answer: hi want to be fwends
Step-by-step explanation:
There can 3 songs to be played for per quarter.
What is unit conversion?A unit conversion expresses the same property as a different unit of measurement.
Given that, It cost Sean 3.75 to play 45 songs on an old jukebox. The jukebox only accepts quarters.
Converting $3.75 into quarters, ($1 = 4 quarters)
$3.75 = 3+0.75
= 3x4+0.75
= 12+3
= 15 quarters
So, he played 45 songs in 15 quarters
Therefore, in 1 quarters = 45/15
= 3
Hence, There can 3 songs to be played for per quarter.
For more references on unit conversion, click;
https://brainly.com/question/19420601
#SPJ5
