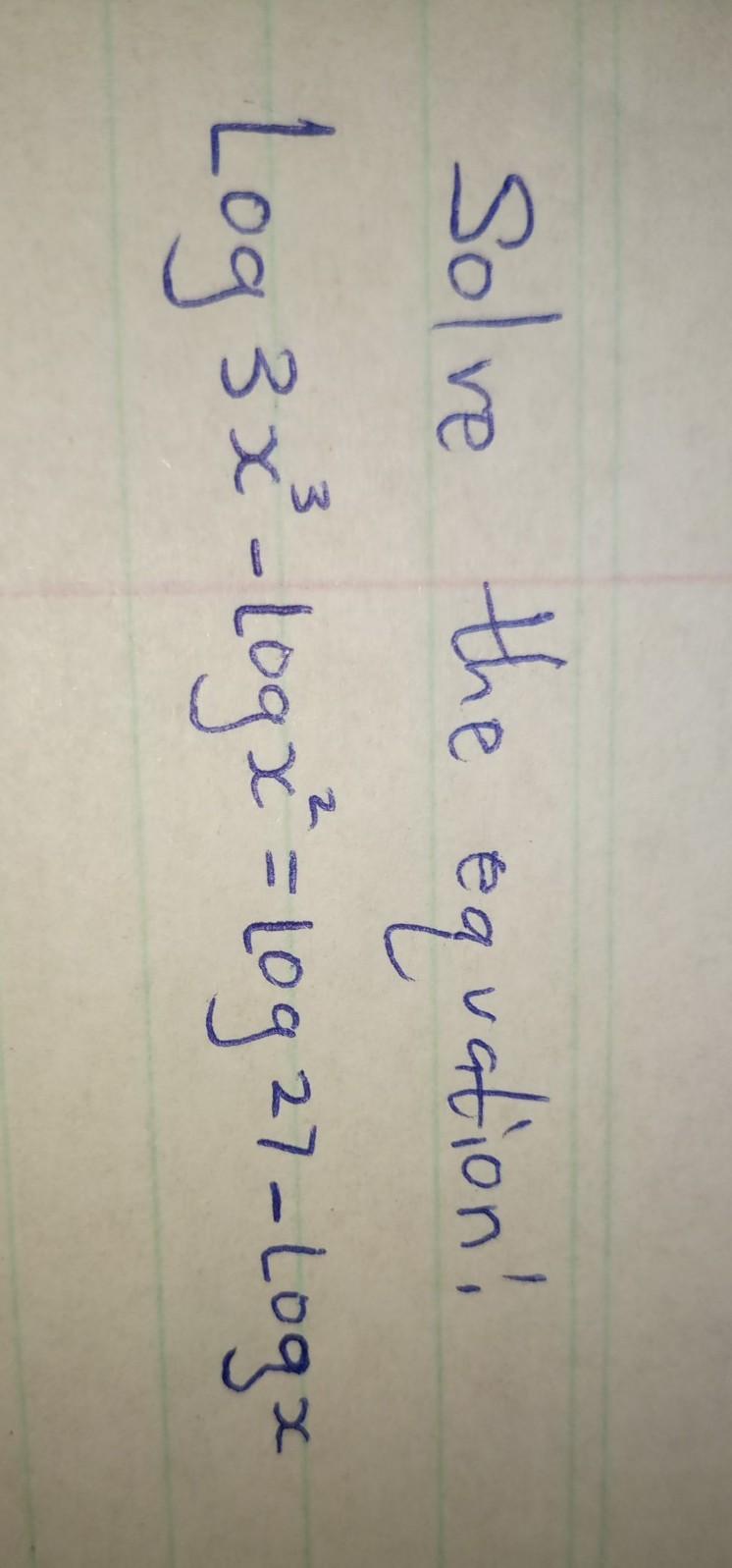please answer this question​

Answer:

transitive property

Step-by-step explanation:

Answer:

62

Step-by-step explanation:

Just do 5/8 = 40/x, and cross-multiply to get:

320 = 5x,

And x will be equal to 62

We have a total of seven 4-tuples that satisfy the given relation.The given relation is {(a,b,c,d) | a,b,c,d∈!+ , a+b+c+d = 6}. It can be understood as the set of 4-tuples (a, b, c, d) such that a, b, c, and d are positive integers and their sum is equal to 6.

Let's now list all the possible 4-tuples that satisfy the given relation. The possible combinations are as follows: (1, 1, 1, 3), (1, 1, 2, 2), (1, 2, 1, 2), (2, 1, 1, 2), (1, 2, 2, 1), (2, 1, 2, 1), and (2, 2, 1, 1).

Here's a brief explanation on how these 4-tuples were obtained. Let a, b, c, and d be positive integers such that a+b+c+d = 6. The least possible value that each variable can take is 1.

So, we start with a=1 and find all possible values of (b, c, d) that satisfy the given equation. Then, we move to a=2 and repeat the process. Finally, we list all the possible 4-tuples that we obtained.

Thus, we have a total of seven 4-tuples that satisfy the given relation.

For more question on integers

https://brainly.com/question/929808

#SPJ8

Answer:

7.2 million dollars

Step-by-step explanation:

The domain of the function the complete set of possible values of the independent variable. In this case the domain includes all real numbers except 189.

From;

T(p) = 0.50 (p - 189)

When p = 203.4 million dollars

T(p) = 0.50 (203.4 - 189)

T(p) = 7.2 million dollars

The length and width of the rectangle with a perimeter of 378ft are 168ft and 21ft respectively.

The formula used in calculating the perimeter of a rectangle is expressed as;

P = 2( l + w )

Where l is length and w is width.

Given the data in the question;

Let 'x' represent the width of the rectangle.

Plug the given values into perimeter formula and solve for x .

P = 2( l + w )

378 = 2( 8x + x )

378 = 2( 9x )

378 = 18x

18x = 378

x = 378/18

x = 21

Now, we find the length and width of the rectangle.

Width of the rectangle w = x = 21ft

Length of the rectangle l = 8x = 8( 21 ) = 168ft

Therefore, the width of the rectangle is 21ft while its length is 168ft.

Learn more about area of rectangle here: https://brainly.com/question/27612962

#SPJ1

Answer:

3

Step-by-step explanation:

1/4 just scale up the 4 to a 12 4*3=12  so (1*3)/(4*3)=3/12=1/4

Answer:

0.0228 = 2.28% probability that any shopper selected at random spends more than $80 per week.

88.54% of shoppers are expected to spend between $30 and 80 per week.

Step-by-step explanation:

Normal Probability Distribution

Problems of normal distributions can be solved using the z-score formula.

In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:

\(Z = \frac{X - \mu}{\sigma}\)

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

Normally distributed with a mean of $50 and a standard deviation of $15.

This means that \(\mu = 50, \sigma = 15\)

Find the probability that any shopper selected at random spends more than $80 per week?

This is 1 subtracted by the p-value of Z when X = 80. So

\(Z = \frac{X - \mu}{\sigma}\)

\(Z = \frac{80 - 50}{15}\)

\(Z = 2\)

\(Z = 2\) has a p-value of 0.9772

1 - 0.9772 = 0.0228

0.0228 = 2.28% probability that any shopper selected at random spends more than $80 per week.

Find the percentage of shoppers who are expected to spend between $30 and 80 per week?

The proportion is the p-value of Z when X = 80 subtracted by the p-value of Z when X = 30.

X = 80

\(Z = \frac{X - \mu}{\sigma}\)

\(Z = \frac{80 - 50}{15}\)

\(Z = 2\)

\(Z = 2\) has a p-value of 0.9772

X = 30

\(Z = \frac{X - \mu}{\sigma}\)

\(Z = \frac{30 - 50}{15}\)

\(Z = -1.33\)

\(Z = -1.33\) has a p-value of 0.0918

0.9772 - 0.0918 = 0.8854

0.8854*100% = 88.54%

88.54% of shoppers are expected to spend between $30 and 80 per week.

Answer:

Step-by-step explanation:

1 Kg of carrot = 40 p

1 1/2 Kg of carrot = 40 * \(\frac{3}{2}\)  = 20 * 3 = 60 p  = £ 0.60

1 kg of potato = 52 p

3 kg of potato = 52 *3 = 156 p =  £1.56

1 box of tea bags = 90 p

Number of boxes for  £1.80 = 1.80 ÷ 0.90  = 2 boxes

4 packs of yogurt =  £4.80

1 pack of yogurt   = 4.80 ÷ 4 =  £1.20

Total = 0.60 + 1.56 + 1.80 +4.80 =  £ 8.76

When selecting 2 letters from the set {A, B, C, D}, considering that the order matters, we can use the concept of permutations to calculate the number of possible arrangements.

The number of ways to arrange 2 letters from a set of 4 can be calculated using the formula for permutations:

P(n, r) = n! / (n - r)!

Where n is the total number of items (in this case, 4) and r is the number of items being selected (in this case, 2).

Using this formula, the number of ways to arrange 2 letters from A, B, C, D is:

P(4, 2) = 4! / (4 - 2)!

= 4! / 2!

= (4 x 3 x 2 x 1) / (2 x 1)

= 24 / 2

= 12

Therefore, there are 12 possible ways to arrange 2 letters selected from A, B, C, D when considering that the order matters.

~~~Harsha~~~

Answer:

Step-by-step explanation:

When selecting 2 letters from the set {A, B, C, D} and considering that the order matters, we can determine the number of possible arrangements using the concept of permutations.

The number of ways to arrange 2 letters from a set of 4 can be calculated using the formula for permutations:

P(n, r) = n! / (n - r)!

where P(n, r) represents the number of permutations of r objects chosen from a set of n objects.

In this case, we have n = 4 (the total number of letters) and r = 2 (the number of letters to be selected).

Using the formula, we can calculate:

P(4, 2) = 4! / (4 - 2)!

       = 4! / 2!

       = (4 × 3 × 2 × 1) / (2 × 1)

       = 24 / 2

       = 12

Therefore, there are 12 different ways to arrange 2 letters chosen from the set {A, B, C, D} when the order matters.

Since ΔABC and ΔACD are similar triangles, therefore the length of AC is 18 m.

Similar triangles are triangles with corresponding sides that have the same ratio.

Thus:

AD is parallel to BC (bases of a trapezoid are parallel)

Therefore:

∠ACB = ∠CAD (alternate interior angles)

This implies that, ΔABC ~ ΔACD by AA similarity theorem.

Thus:

AC/DA = CB/AC

Substitute

AC² = 12 × 27

AC = √324

AC = 18 m

Therefore, since ΔABC and ΔACD are similar triangles, therefore the length of AC is 18 m.

Learn more about similar triangles on:

brainly.com/question/11899908

#SPJ1

Answer:

increases by 30

Step-by-step explanation: its right

Answer:

b = -18

Step-by-step explanation:

(3 + 4i) (-3-2i)

When we foil:

-9 + -6i + -12i + -8i^2

-8i^2 = +8

Combine like terms:

-1 + -18i

Answer:

1191 cm²

Step-by-step explanation:

Area of parallelogram = base X vertical height.

Call the vertical line h.

h/ sin 80  =  7/ sin 10

h = (7 sin 80) / sin 10

= 39.7.

Area of parallelogram = 30 X 39.7

= 1191 cm²

The Area of Parallelogram whose side length is 30 cm is 1,190.952 square cm.

Given:

Side length = 30 cm

Using Trigonometry

tan 80 = P / Base

5.6712 = P / 7

P = 39.6984 cm

Using the formula for Area of parallelogram

= Base x height

= 30 x 39.6984

= 1,190.952 square cm.

Therefore, the area is 1,190.952 square cm.

Learn more about Area of Parallelogram here:

https://brainly.com/question/9148769

#SPJ6

Answer:

:w=1/3(a)

Step-by-step explanation:

w = 1/3 × a

If Lago is 150lb, Jeb's  =

1/3 x 150 = 50 lb

If Lago is 60lb, Jeb's  =

1/3 x 60 = 20lb

Answer:

f(4) = -129

Step-by-step explanation:

Substitute the value of x which is 4

f(x) = -2x4 + 6x3 - 3x + 11

f(4) = -2(4)4 + 6(4)3 - 3(4) + 11

f(4) = -2(256) + 6(64) - 12 + 11

f(4) = -512 + 384 - 1

f(4) = -128 - 1

f(4) = -129

The inverse of matrix A, if it exists, is:

A^(-1) = [7/43, 2/43; 10/43, 9/43]

To find the inverse of a matrix A, we need to determine if the matrix is invertible by calculating its determinant. If the determinant is non-zero, then the matrix has an inverse.

Given the matrix A = [9, -2; -10, 7], we can calculate its determinant as follows:

det(A) = (9 * 7) - (-2 * -10)

= 63 - 20

= 43

Since the determinant is non-zero (43 ≠ 0), we can proceed to find the inverse of matrix A.

The formula to calculate the inverse of a 2x2 matrix is:

A^(-1) = (1/det(A)) * [d, -b; -c, a]

Plugging in the values from matrix A and the determinant, we have:

A^(-1) = (1/43) * [7, 2; 10, 9]

Simplifying further, we get:

A^(-1) = [7/43, 2/43; 10/43, 9/43].

For more such questions on Inverse of matrix:

https://brainly.com/question/27924478

#SPJ8

Answer:

Back Prism: 60

Front Prism: 90

Total Volume: 150

Step-by-step explanation:

Answer:

x = 5.5

Step-by-step explanation:

2x + 3 - 4 = 10

2x - 1 = 10

2x = 11

x = 5.5

Let's check

2(5.5) + 3 - 4 = 10

11 + 3 - 4  = 10

14 - 4 = 10

10 = 10

So, x = 5.5 is the correct answer.

Answer: x = 5.5

Step-by-step explanation:

To solve, we will isolate the variable x.

      Given:

             2x + 3 - 4 = 10

      Combine like terms on the left side:

             2x - 1 = 10

      Add 1 to both sides of the equation:

             2x = 11

      Divide both sides of the equation by 2:

             x = 5.5

Step-by-step explanation:

there is nothing missing. this is a complete proof.

yes, the various steps are correct.

Average rate of return for 3D Printer is 4% and for Truck is 9%.

Average income = Estimated total income/ useful life.

For 3D Printer,

Average Income = 4160/ 4

Average Income = $1040

For Truck,

Average Income = 15120/ 7

Average Income = $2160

Average Investment = (Investment + residual value)/ 2

For 3D Printer,

Average Investment = (52000 + 0)/ 2

Average Investment = $26000

For Truck,

Average Investment = (48000 + 0)/ 2

Average Investment = $24000

Average rate of return = Average Income/ Average Investment

For 3D Printer,

Average rate of return = 1040/26000

Average rate of return = 4%

For Truck,

Average rate of return = 2160/24000

Average rate of return = 9%

Hence, average rate of return for 3D Printer is 4% and for Truck is 9%.

To learn more about rate of return, visit:

brainly.com/question/28744270

#SPJ4

The probability of the sample mean being less than 25.3 is given as follows:

0.9713 = 97.13%.

The sample mean would not be considered unusual, as it has a probability that is greater than 5%.

The z-score of a measure X of a normally distributed variable that has mean represented by \(\mu\) and standard deviation represented by \(\sigma\) is obtained by the equation presented as follows:

\(Z = \frac{X - \mu}{\sigma}\)

The parameters for this problem are given as follows:

\(\mu = 25, \sigma = 1.3, n = 68, s = \frac{1.3}{\sqrt{68}} = 0.1576\)

The probability of a score less than 25.3 is the p-value of Z when X = 25.3, hence:

Z = (25.3 - 25)/0.1576

Z = 1.9

Z = 1.9 has a p-value of 0.9713.

More can be learned about the normal distribution at https://brainly.com/question/25800303

#SPJ1

The perimeter of the lot = (8x - 8) meters

The plot of of land is triangular in shape

The side lengths of the triangle are x, (3x - 3), and (4x - 5)

The perimeter of a shape is the sum of all the side lengths

Perimeter = x + (3x - 3) + (4x - 5)

Perimeter = x + 3x + 4x - 3 - 5

Perimeter = 8x - 8

The perimeter of the lot = (8x - 8) meters

We will see that Mrs. Cardenas pays $63.44 weekly.

Here we know that the cost of the insurance is $9,450.20, this would be the 100%.

We know that the company pays for 65% of it, meaning that Mrs. Cardenas pays for the other 35%.

Then we need to find how much is the 35% of $9,450.20, it is given by:

(35%/100%)*$9,450.20 = 0.35*$9,450.20 = $3,307.57

This means that Mrs. Cardenas pays $3,307.57 annually. But we want to know how much she pays weekly.

In a year, there are near 52.14 weeks, so we divide the above quantity by 52.14

($3,307.57)/(52.14) = $63.44

Mrs. Cardenas pays $63.44 weekly.

If you want to learn more about percentages, you can read:

https://brainly.com/question/843074

Hello!

surface area

= 2(4 x 2) + 2(12 x 4) + 2(12 x 2)

= 160cm²

Step-by-step explanation:

\(f(f(x)) = f( {x}^{2} + 4)\)

\( = {( {x}^{2} + 4) }^{2} + 4\)

\( = {x}^{4} + 4 {x}^{2} + 16 + 4\)

\( = {x}^{4} + 8 {x}^{2} + 20\)

Answer:

x>= 11 or x>10

Step-by-step explanation:

Absolute value can be used to represent the positive counterpart of a negative number. In this case, we are asked to find a number that is less than -10, meaning from -11 to negative infinity. Since we are asked to take absolute value, we would take |-11| which equals 11, and |-∞| = ∞.

So Amy graphed a value on the number line that is greater than or equal to 11, or any value greater than 10.

*Infinity is not a real number, it represents the largest number possible, which doesn't exist since numbers can continue on forever, so it can be disregarded.*

the answer would be c because the angles are equal to each other