Answers
Answer:
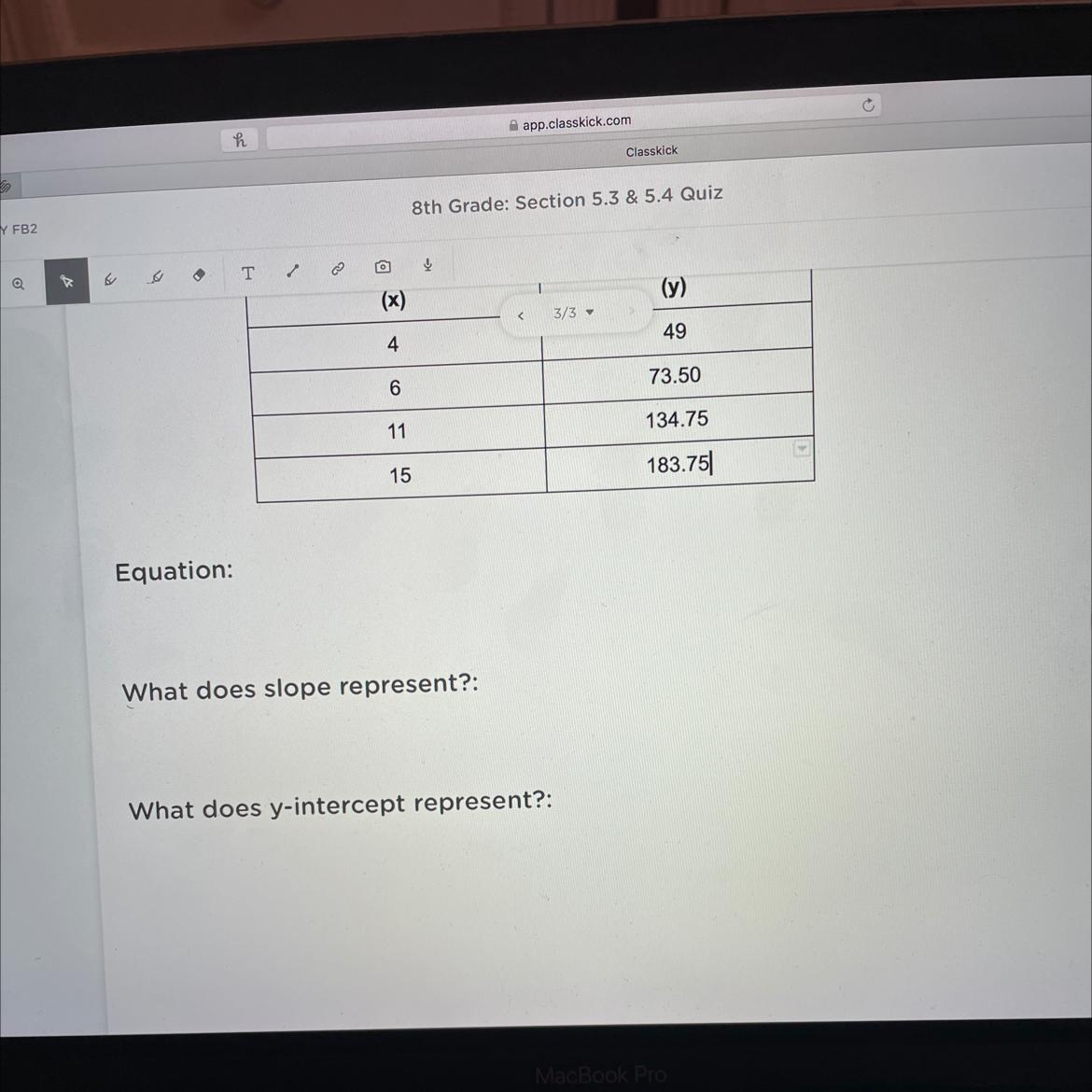
y=12.25x
i cannot see the question but the slope will be the increase of the certain product
the y is the dependent factor that will increase due to the slope/x-intercept
Step-by-step explanation:
Related Questions
Your goal is to run a mean of 45 minutes per day for a week. For the first six days, you run 38, 40, 40, 42, 43, and 50 minutes. How many minutes must you run on the seventh day to reach your goal exactly?
CLEAR CHECK
28 minutes
62 minutes
4216 minutes
17 minutes
Answers
Answer:
The answer is 62 minutes
Match the question with the answer (e.G. 1 + C) 26 x 5 161 2. 25 x 6 130 3. 22 x 6 168 4. 21 x 8 150 5. 23 x 7 132 Answers: 1 + 2 + 3 + 4 + 5 +
Answers
Answer:
1+B,2+D,3+E,4+C and 5+A
Step-by-step explanation:
(A)161 (B)130 (C)168 (D)150 (E)132
1. 26 x 5=130
This is Option B, therefore we have the match:1+B
2. 25 x 6=150
This is Option D, therefore we have the match:2+D
3. 22 x 6=132
This is Option E, therefore we have the match: 3+E
4. 21 x 8=168
This is Option C, therefore we have the match: 4+C
5. 23 x 7=161
This is Option A, therefore we have the match:5+A
can you please help me
Answers
The parent factors are the colours white or gray
Below is an image to represent the Tree diagram
It shows that for a white shirt Marcus can buy either a white medium and white large sizes
It also shows that for a gray shirt Marcus can also buy a gray medium and a gray large shirt
With this information, we can conclude that the possible answer to the question is the last OPTION D

Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s).
Find the inverse of the given function.
f() = -kvo + 3, < > -3
Answers
Answer:
\(f'(x) = 4x^2 - 3\) for \(x \le -3\)
Step-by-step explanation:
See attachment for proper question
Given
\(f(x) = -\frac{1}{2}\sqrt{x + 3}\)
For
\(x \ge -3\)
Required
Determine the inverse function
\(f(x) = -\frac{1}{2}\sqrt{x + 3}\)
Replace f(x) with y
\(y = -\frac{1}{2}\sqrt{x + 3}\)
Swap the positions of x and y
\(x = -\frac{1}{2}\sqrt{y + 3}\)
Multiply both sides by -2
\(-2 * x =-2 * -\frac{1}{2}\sqrt{y + 3}\)
\(-2x =\sqrt{y + 3}\)
Square both sides
\((-2x)^2 =(\sqrt{y + 3})^2\)
\(4x^2 =y + 3\)
Make y the subject
\(y = 4x^2 - 3\)
The inverse has been solved. So, we need to replace y with f'(x)
\(f'(x) = 4x^2 - 3\)
Next, is to determine the interval
\(x \ge -3\)
Change inequality to \(\le\)
\(x \le -3\)
Hence, the inverse function is:
\(f'(x) = 4x^2 - 3\) for \(x \le -3\)

In the northern hemisphere, the ratio of the area of land to the area of land to the area of water is 2:3
A. work out what percentage of the area of the northern hemisphere is the land?
20% of the area of the southern hemisphere is land.
B. work out the ratio of the area of land to the area of water in the southern hemisphere.
Answers
The percentage of the area of the northern hemisphere that is the land is 40%.
The ratio of the area of land to the area of water in the southern hemisphere will be 3:2.
How to illustrate the information?It should be noted that in northern hemisphere, the ratio of the area of land to the area of land to the area of water is 2:3, the percentage of the area of the northern hemisphere is the land will be:
= 2 / (2+3) × 100
= 2/5 × 100
= 40%
It should be noted that the ratio of the area of land to the area of water in the southern hemisphere will be 3:2. This is the inverse of 2:3.
Learn more about ratio on:
brainly.com/question/2328454
#SPJ1
In AJKL, j = 74 cm, k = 14 cm and l=80 cm. Find the measure of ZJ to the nearestdegree.
Answers
To answer this question we first draw the triangle to help us:
As a note on the problem: This is not necessarily the triangle we have, we drew just to helps us solve it.
Now, to find the angle J we can use the law of cosines:
\(j^2=k^2+l^2-2kl\cos J\)Plugging the values we have and solving for J we have:
\(\begin{gathered} 74^2=14^2+80^2-2(14)(80)\cos J \\ 2(14)(80)\cos J=14^2+80^2-74^2 \\ \cos J=\frac{14^2+80^2-74^2}{2(14)(80)} \\ J=\cos ^{-1}(\frac{14^2+80^2-74^2}{2(14)(80)}) \\ J=60 \end{gathered}\)Therefore the angle J is 60°.

I’m not really sure what to choose..

Answers
Answer:
i think it would be SAS, sorry if I'm wrong!
Step-by-step explanation:
9514 1404 393
Answer:
SAS
Step-by-step explanation:
The hash marks on the segments of the triangle indicate congruence. The "one hash mark" segments are congruent to each other, and the "two hash marks" segments are congruent to each other. That is, two corresponding sides are marked congruent.
Similarly, the arc on the angle indicates the angle is congruent to one with a similar mark. We notice that the marked angle is between the sides that have hash marks. So, we have, in order around the triangle, congruent Sides, Angles, Sides. The appropriate choice is ...
SAS
T/F: a large p-value in a test will favor a rejection of the null hypothesis.
Answers
A test's large p-value does not necessarily mean that the null hypothesis should be accepted.
In a test, a low P-value will favor rejecting the null hypothesis.
The P-value approach evaluates whether something is "likely" or "unlikely," assuming that the null hypothesis is correct, by calculating the probability of observing a test statistic that is more extreme in the direction of the alternative hypothesis than the one actually seen. If the P-value is low, such as less than, it is "unlikely" (or equal to) α.
The null hypothesis is disregarded in favor of the alternative hypothesis if the P-value is less than (or equal to) α. Additionally, the null hypothesis is not disproved if the P-value is higher than α.
As a result, the right response is false.
To learn more about the null hypothesis, refer:-
https://brainly.com/question/28920252
#SPJ4
Find values of m so that the function y xm is a solution of the given differential equation. x^2y''-7xy' 15y=0
Answers
If \(y=x^m\) is a solution to the ODE
\(x^2 y'' - 7xy' + 15y = 0\)
then substituting \(y\) and its derivatives
\(y' = mx^{m-1} \text{ and } y'' = m(m-1)x^{m-2}\)
gives
\(m(m-1)x^2x^{m-2} - 7mxx^{m-1} + 15x^m = 0\)
\(m(m-1)x^{m} - 7mx^{m} + 15x^m = 0\)
\((m(m-1) - 7m + 15)x^{m} = 0\)
We ignore the trivial case of \(y=x^m=0\). Solve for \(m\).
\(m(m-1) - 7m + 15 = 0\)
\(m^2 - 8m + 15 = 0\)
\((m - 3) (m - 5) = 0\)
\(\implies \boxed{m=3} \text{ or } \boxed{m=5}\)
derivative of (a^x/Log a)?
Answers
\(\sf{\dfrac{a^x}{log(a)} }\)
(OR)\(\sf{\dfrac{a^x}{ln(a)} }\)
\(\large\bold{\underline{\underline{Solution:-}}}\)\(\sf{Let\ y=\dfrac{a^x}{ln(a)} }\)
\(\sf{=\dfrac{d}{dx}\bigg[\dfrac{a^x}{ln(a)} \bigg] }\)
(Linear differentiation)\(\sf{=\dfrac{1}{ln(a)}.\dfrac{d}{dx}(a^x) }\)
\(\sf{=\dfrac{ln(a)a^x}{ln(a)} }\)
\(\boxed{\sf{=a^x}}\)
\(\large\bold{\underline{\underline{Applied:-}}}\)✭ Linear differentiation→ \(\sf{[a.b(x)+c.d(x)]'=a.b'(x)+c.d'(x)}\)
✭ Exponential function rule
→ \(\sf{(a^x)'=ln(a).a^x}\)
Answer:
a^x.
Step-by-step explanation:
y = a^x / log a
Assuming the log is to the base e:
y = (1/ log a) * a^x
Derivative of a^x:
Let u = a^x
log u = log a^x
log u = x log a
1/u * du/dx = log a
du/dx = = u * log a
y = (1 / log a) * u
so dy/du = 1/log a
and dy/dx = dy/du * du/dx
= (1/log a )* log a u
= u
= a^x.
What is the radius of F?

Answers
The radius of circle F is equal to: C. 12.
What is Pythagorean theorem?In Mathematics and Geometry, Pythagorean's theorem is modeled or represented by the following mathematical equation (formula):
a² + b² = c²
Where:
a, b, and c represents the length of sides or side lengths of any right-angled triangle.
By substituting the given side lengths into the formula for Pythagorean's theorem, we have the following;
a² + b² = c²
a² + 9² = 15²
a² = 225 - 81
a = √144
a = 12 units.
Read more on Pythagorean theorem here: brainly.com/question/15430861
#SPJ1
A Ferris wheel makes five full rotations and then stops to let more riders on How many degrees in total did the Ferris
wheel rotate before stopping?
degrees
Answers
Answer:
1800 Degrees
Step-by-step explanation:
360 equals a full rotation I Think.
The wheel made, 1800° in 5 rotation.
What is rotation?The meaning of rotation is the action or process of rotating on or as if on an axis or center.
Given that, A Ferris wheel makes five full rotations and then stops
Since, we know that there are 360° in one rotation,
A wheel makes 360° if it rotates for one time.
Therefore, in 5 rotation, = 5 × 360° = 1800°
Hence, the wheel made, 1800° in 5 rotation.
For more references on rotation, click;
https://brainly.com/question/12091224
#SPJ2
A ∠A and ∠ B ∠B are supplementary angles. If m ∠ A = ( 8 x + 6 ) ∘ ∠A=(8x+6) ∘ and m ∠ B = ( 7 x + 24 ) ∘ ∠B=(7x+24) ∘ , then find the measure of ∠ B ∠B.

Answers
Answer:
< B = 94
Step-by-step explanation:
Remark
You should edit the question. The way you wrote it, , it looks like you have to square two binomials. That isn't the way it is given I don't think. You are told that A and B are supplementary. That means
A+B = 180
Equation
(8x + 6) + (7x + 24) = 180 Remove the brackets
Solution
8x + 6 + 7x + 24 = 180 Collect like terms
15x + 30 = 180 Subtract 30 from both sides
15x = 180 - 30
15x = 150 Divide by 15
x = 150 / 15
x = 10
Answer
What you need is <B
<B = 7x + 24
<B = 7*10 + 24
<B = 70 + 24
<B = 94
|x+4|+3=17 (solve for x)
Answers
Answer:
x = 10, -18
Step-by-step explanation:
Hope it helps :)
What is -12(k+4)=60? Solve for k.
Answers
Hello there & welcome to Brainly!
You are solving for the variable, k. Isolate the variable, k. Note the equal sign, what you do to one side, you do to the other.
First, distribute -12 to all terms within the parenthesis:
-12(k + 4) =
-12 * k = -12k
-12 * 4 = -48
-12k - 48 = 60
Isolate the variable, k. Note the equal sign, what you do to one side, you do to the other. Do the opposite of PEMDAS.
PEMDAS is the order of operation, and equal:
Parenthesis
Exponents (& Roots)
Multiplication
Division
Addition
Subtraction
First, add 48 to both sides of the equation:
-12k - 48 (+48) = 60 (+48)
-12k = 60 + 48
-12k = 108
Next, divide -12 from both sides of the equation:
(-12k)/-12 = (108)/-12
k = 108/-12
k = -9
k = -9 is your answer.
~
Recall that the cigarette industry requires that models in cigarette ads must appear to be at least 25 years old. Also recall that a sample of 50 people is randomly selected at a shopping mall. Each person in the sample is shown a "typical cigarette ad" and is asked to estimate the age of the model in the ad. The p -value for testing H0 versus Ha can be calculated to be 0.0038.
Determine whether H0 would be rejected at each of ? = .10, ? = .05, ? = .01, and ? = .001. (Round your answer to 4 decimal places.)
p-value Reject H0 at ? =
Answers
The p-value for testing H0 (null hypothesis) versus Ha (alternative hypothesis) is 0.0038. We need to determine whether H0 would be rejected at different significance levels: α = 0.10, α = 0.05, α = 0.01, and α = 0.001.
To make the decision, we compare the p-value with the chosen significance level. If the p-value is less than or equal to the significance level, we reject H0. Otherwise, we fail to reject H0.
At α = 0.10: Since the p-value (0.0038) is less than 0.10, we reject H0.
At α = 0.05: Since the p-value (0.0038) is less than 0.05, we reject H0.
At α = 0.01: Since the p-value (0.0038) is greater than 0.01, we fail to reject H0.
At α = 0.001: Since the p-value (0.0038) is greater than 0.001, we fail to reject H0.
In summary:
H0 would be rejected at α = 0.10 and α = 0.05.
H0 would not be rejected at α = 0.01 and α = 0.001.
Please note that the decision to reject or fail to reject the null hypothesis depends on the chosen significance level, and different levels of significance can lead to different conclusions.
Learn more about hypothesis testing here: brainly.com/question/17099835
#SPJ11
Isabella wants to advertise how many chocolate chips are in each Big Chip cookie at her bakery. She randomly selects a sample of 61 cookies and finds that the number of chocolate chips per cookie in the sample has a mean of 14.3 and a standard deviation of 2.2. What is the 98% confidence interval for the number of chocolate chips per cookie for Big Chip cookies
Answers
The 98% confidence interval for the number of chocolate chips per cookie in Big Chip cookies is approximately 13.5529 to 15.0471 chips.
To find the 98% confidence interval for the number of chocolate chips per cookie in Big Chip cookies, we'll use the t-distribution since the sample size is relatively small (n = 61) and we don't know the population standard deviation.
The formula for the confidence interval is:
\(CI = \bar X \pm t_{critical} \times \dfrac{s } {\sqrt{n}}\)
where:
X is the sample mean,
\(t_{critical\) is the critical value for the t-distribution corresponding to the desired confidence level (98% in this case),
s is the sample standard deviation,
n is the sample size.
First, let's find the critical value for the t-distribution at a 98% confidence level with (n-1) degrees of freedom (df = 61 - 1 = 60). You can use a t-table or a calculator to find this value. For a two-tailed 98% confidence level, the critical value is approximately 2.660.
Given data:
X (sample mean) = 14.3
s (sample standard deviation) = 2.2
n (sample size) = 61
\(t_{critical\) = 2.660 (from the t-distribution table)
Now, calculate the confidence interval:
\(CI = 14.3 \pm 2.660 \times \dfrac{2.2} { \sqrt{61}}\\CI = 14.3 \pm 2.660 \times \dfrac{2.2} { 7.8102}\\CI = 14.3 \pm 0.7471\)
Lower bound = 14.3 - 0.7471 ≈ 13.5529
Upper bound = 14.3 + 0.7471 ≈ 15.0471
To know more about confidence intervals follow
https://brainly.com/question/32452107
#SPJ4
1.1x10^5 in standard notation
Answers
Answer:
110000
Step-by-step explanation:
first, expand 10^5, which is 100000
use a calculator (or long multiplication) to multiply 1.1*100000, which is 110000
210 sheets of paper is 7cm thick. How thick of a pile would 1260 sheets make?
Answers
Study the scenario described below and answer all questions that follow. Firms achieve their missions in three conceptual ways: (1) differentiation, (2) costs leadership, and (3) response. In this regard, operations managers are called on to deliver goods and services that are (1) better, or at least different, (2) cheaper, and (3) more responsive. Operations managers translate these strategic concepts into tangible tasks to be accomplished. Any one or combination of the three strategy options can generate a system that has a unique advantage over competitors (Heizer, Render and Munson, 2017:74). P\&B Inc., a medium-sized manufacturing family-owned firm operates in a market characterised by quick delivery and reliability of scheduling as well as frequent dramatic changes in design innovation and customer demand. As the operations analysts at P\&B Inc., discuss how you would prioritise for implementation the following FOUR (4) critical and strategic decision areas of operations management as part of P\&B's 'input-transformation-output' process to achieve competitive advantage: 1. Goods and service design 2. Human resources and job design 3. Inventory, and 4. Scheduling In addition to the above, your discussion should include an introduction in which the strategy option implicated by the market requirements is comprehensively described
Answers
The prioritized critical decision areas for P&B Inc. to achieve competitive advantage are goods and service design, human resources and job design, inventory management, and scheduling, aligned with a response strategy.
To achieve a competitive advantage in a market characterized by quick delivery, reliability of scheduling, and frequent design innovation and customer demand changes, P&B Inc. needs to prioritize critical decision areas.
Goods and service design should focus on creating innovative and differentiated products/services that meet customer needs. Human resources and job design should ensure a skilled and motivated workforce capable of delivering high-quality outputs.
Inventory management is crucial to balance stock levels, minimize costs, and meet customer demands promptly. Scheduling should prioritize efficient resource allocation and sequencing of tasks to optimize production and meet customer deadlines.
By effectively managing these decision areas, P&B Inc. can align its operations with a response strategy, delivering quick and reliable outcomes while adapting to market dynamics.
This strategic approach allows the company to differentiate itself, attract customers, and maintain a competitive edge in the industry.
Learn more about critical here: https://brainly.com/question/17259837
#SPJ11
Write the slope-intercept form of the equation of the line through the given point with the givenslope.8) through: (4,4), slope = 27) through: (3,-1), slope = -2/3
Answers
Let's begin by listing out the information given to us:
slope-intercept form of the equation of the line is given by:
Given that tanθ almost equal to≈ 2.773 where 0<θ<π2, find the values of sinθ and cosθ. Show work.
Answers
Step-by-step explanation:
the given data is
tanθ = 2.773 and 0<θ<π/2
this implies θ = tan inverse(2.773)
⇒ θ = 70.16°
Therefore, sinθ = sin70.16° = 0.9406
similarly,cosθ = cos70.16° = 0.3393
therefore, values of sinθ and cosθ are 0.9406 and 0.3393 respectively.
find the p-value (to two significant digits) for the following test. h0: μ ≤ 0, h1: μ > 0, σ = 1, z = 1.5 hint: the population follows the standard normal distribution.
Answers
The p-value for the given test is approximately 0.067, rounded to two significant digits. This was calculated by finding the area to the right of z=1.5 under the standard normal distribution.
It is given that Null hypothesis: H0: μ ≤ 0, Alternative hypothesis: H1: μ > 0, Population standard deviation: σ = 1, Test statistic: z = 1.5
To find the p-value, we need to calculate the probability of observing a z-value of 1.5 or greater under the null hypothesis. Since the population follows the standard normal distribution, we can use a standard normal table or a calculator to find this probability.
Using calculator, we can find that the area to the right of z = 1.5 is approximately 0.0668 (rounded to four decimal places).
Since this is a one-tailed test with the alternative hypothesis in the right tail, the p-value is equal to the area in the right tail beyond the observed z-value. Therefore, the p-value for the test is approximately 0.067 (rounded to two significant digits).
So, the p-value for the given test is 0.067 (rounded to two significant digits).
To know more about p-value:
https://brainly.com/question/30461126
#SPJ4
This question require two answers

Answers
Answer:
2/3 and -4
Step-by-step explanation:
using the quadratic formula,
-b +_root(b squared - 4(3)(-8) the whole divided by 2a
Step-by-step explanation:
hope this will help you.

a rectangular room is 3 3 times as long as it is wide, and its perimeter is 56 56 meters. find the dimension of the room.
Answers
Consequently, the room has a 7 meter width. The room's length is
\(= 7 * 3 meters = 21 meters\)
What is rectangle?
A rectangle in Euclidean plane geometry is a quadrilateral with four right angles. You might also describe it as follows: a quadrilateral that is equiangular, which indicates that all of its angles are equal. The parallelogram might also have a straight angle. Squares are rectangles with four equally sized sides. A quadrilateral of the shape of a rectangle has four 90-degree vertices and equal parallel sides. As a result, it is sometimes referred to as an equirectangular rectangle. Because its opposite sides are equal and parallel, a rectangle is also known as a parallelogram.
Given that the length of the rectangular space is three times its breadth
The chamber has a 56-meter perimeter.
Assume that the room's width is x.
As a result, the room is three times as long.
The room's perimeter is now equal to 2(3x + x).
\(Here, 2(3x + x) = 56\\ 2 * 4x = 56\\ 8x = 56\\ x = 7.\)
Consequently, the room has a 7 meter width.
The room's length is
\(= 7 * 3 meters\\= 21 meters\)
To know more about Rectangle visit:
https://brainly.com/question/29123947
#SPJ4
After an alcoholic beverage is consumed, the concentration of alcohol in the bloodstream (blood alcohol concentration, or BAC) surges as the alcohol is absorbed, followed by a gradual decline as the alcohol is metabolized. The function C(t)=0.135 t e^{-2.802 t}C(t)=0.135te −2.802t models the average BAC, measured in g/dL, of a group of eight male subjects t hours after rapid consumption of 15 mL of ethanol (corresponding to one alcoholic drink) What is the maximum average BAC during the first 3 hours? When does it occur?
Answers
It gradually decreases as alcohol is metabolized. The function C(t)=0.135 t e^{-2.802 t}models the mean BAC measured in g/mL.
The maximum average BAC during 3 hours is 0.0001358 g/mL.
f(t) = α t e−βt --(1)
Let's rewrite this in a simple form:
f(t)= α eˡⁿ ᵗ e⁻βt = αe^(ln t −βt)
Since e^x is strictly increasing and it will be maximized exactly when its argument is maximized, so we can maximize instead:
g(t)=ln t −βt
differentiating with respect to t , and g'(t) = 0
g′(t)=1/t − β = 0
=> t =1/β
we have given a function
C(t)=0.135 t e⁻²·⁸⁰²ᵗ
if we compare it with (1) we get
β = 2.802, 0.135 = α
For it's maximized we need to check the second order condition, and that of g will differentiate again , g′′(t)= −1/t² < 0
We have to compute the derivative of C(t):
C′(t) = 0.135 t⋅(−2.802)e⁻²·⁸⁰²ᵗ + 1.35e⁻²·⁸⁰²ᵗ
For optimum at t₀ if C′(t₀)=0 and C′′(t₀)≠0. Here, we have
C′(t₀) = 0.135t₀⋅(−2.802)e⁻²·⁸⁰²ᵗ₀+ 0.135e⁻²·⁸⁰²ᵗ₀ =e⁻²·⁸⁰²ᵗ₀(−0.135* 2.802t₀+ 0.135)=0
It is clear that e⁻²·⁸⁰²ᵗ₀ not equal to zero for all t₀∈R, so that
=> −0.135* 2.802t₀+0.135=0
=> t₀ = 1/2.802 ≈0.36
let us consider t is in hours, so that it makes t₀ =0.36h≈21.41min. This is the only optimum and one should verify it is indeed a maximum, i.e. C′′(t₀)<0.
Now, easily compute the maximum average BAC, which is C(t₀)=C(0.36) = 0.135 (0.36)e⁻²·⁸⁰²⁽⁰·³⁶⁾
= 0.0486(0.3678) = 0.01787508
Hence, the maximum average BAC, is 0.017 g/dL.
Maximum average BAC during the first 3 hours,
t = 3 , C(t)=C(3) = 0.135 (3)e⁻²·⁸⁰²⁽³⁾ = 0.0001358 g/mL
To learn more about Exponential function, refer:
https://brainly.com/question/12626186
#SPJ4
1424 and 2243 are numbers in base 5. add these numbers as it relates to the base 5 system
Answers
In the "ones" place,
4₅ + 3₅ = (7)₅ = (5 + 2)₅ = 10₅ + 2₅ = 12₅
(a number in base 5 can only consist of the digits 0-4; anything larger, which I wrap in parentheses, needs to be split up further)
In the "tens" place, we carry over the 1 from the previous sum:
2₅ + 4₅ + 1₅ = (7)₅ = 12₅
In the "hundreds" place,
4₅ + 2₅ + 1₅ = (7)₅ = 12₅
In the "thousands" place,
1₅ + 2₅ + 1₅ = 4₅
So, we have
1424₅ + 2243₅ = 4222₅
Find all solutions of the equation below.
7^5-3=7^5x-19
Answers
Answer:
7⁵-3=7⁵x- 19
Step-by-step explanation:
16807 - 3 = 7⁵x - 19
16804 = 7⁵x - 19
16804 = 16807x - 1
adding 19 on both sides
16804 + 19 = 16807x - 19 + 19
16823 = 16807x
x = 16823 / 16807
16823 upon 16807 is the x
Determining the End Behavior of a Polynomial Function HELP ASAP !!!!

Answers
Answer:I think degree 4 but im not sure
Step-by-step explanation:
A family of two adults and three children went to a water park. Admission to the water park costs $18 per person. Nora used the expression 2 (18) + 3 (18) to model the total cost for the family, and Alex used the expression 5 (18). Which property of operations makes both of their expressions correct?
Answers
Answer:
The distributive property
Step-by-step explanation:
Nora essentially distributing the parts of the problem.
Please tell me if I'm wrong and I'll fix my answer.
Answer:
its the distributive property
Step-by-step explanation:
i took the
test