Answers
Answer:
A. ≈31.1
B. ≈19.7
Step-by-step explanation:
A. 245/798
B. 157/798
Answer:
Look at step-by-step explanation
Step-by-step explanation:
14a.
There are 798 students total and 245 freshman. To find the percent of freshman, divide 245 by 798:
245/789= 31.1%
Same process for part b. There are 798 students and 157 seniors:
157/789= 20.0%
Related Questions
State the image of the point (3,7) after a reflection in the y-axis:(Blank 1:Blank 2:

Answers
In order to reflect a point over the y-axis, we just need to change the signal of its x-coordinate.
So for the point (3, 7), the reflection over the y-axis would be (-3, 7).
Therefore we have:
Blank 1: -3
Blank 2: 7
The drama club is selling tickets to their play to raise money for the show's expenses.
Each student ticket sells for $7.50 and each adult ticket sells for $10. The drama club
must make no less than $1200 from ticket sales to cover the show's costs. Write an
inequality that could represent the possible values for the number of student tickets
sold, s, and the number of adult tickets sold, a, that would satisfy the constraint.
Answers
The total revenue from adult ticket sales (10a) must be greater than or equal to $1200.
Let's represent the number of student tickets sold as 's' and the number of adult tickets sold as 'a'.
The revenue from student ticket sales can be calculated as 7.50s, and the revenue from adult ticket sales can be calculated as 10a.
To satisfy the constraint that the drama club must make no less than $1200, we can write the following inequality:
7.50s + 10a ≥ 1200
This inequality states that the total revenue from student ticket sales (7.50s) plus the total revenue from adult ticket sales (10a) must be greater than or equal to $1200.
This inequality ensures that the ticket sales generate enough revenue to cover the show's costs. The drama club needs to sell enough tickets, both student and adult, to meet or exceed the minimum revenue requirement of $1200.
For more such answers on revenue
https://brainly.com/question/30760779
#SPJ8
Functions f(x)16x^2
G(x) 1/4 sq root x

Answers
Answer:
x
x
are the same
Step-by-step explanation:
when you plug in g(x) into f(x)
f(x)=16((1/4)(x)^.5)==x
then vice versa
g(x)=(1/4)((16x^2)^.5)==x
They are the same and, therefore, inverses of each other.
Use the figure below to answer the following questions be sure to use appropriate symbol where necessary

Answers
Based on the given pictures:
∠1 is obtuse angle∠2 is acute angle∠ABC is straight angle∠2 name is ∠EBDx = 15x = 13Angle ∠1 has a more than 90° angle, means that it is classified as obtuse angle.
Angle ∠2 has a less than 90° angle, means that it is classified as an acute angle.
∠ABC is a straight angle because it creates a straight line with 180°.
Angle ∠2 can be named as ∠EBD because it was created by lines EB and ED.
∠WXY = 88°
∠WXZ = 4x - 3
∠ZXY = 2x + 1
∠WXY = ∠WXZ + ∠ZXY
88 = (4x - 3) + (2x + 1)
88 = 6x - 2
6x = 90
x = 15
∠HIJ = 108°
IK bisects ∠HIJ
∠HIK = 4x + 2
∠HIJ = 2∠HIK
108 = 2(4x + 2)
108 = 8x + 4
8x = 104
x = 13
Learn more about Angles here: brainly.com/question/28451077
#SPJ1
A backpack is on sale for 30% off . If the sales price is $15.75 , what is the original price to the nearest cent.
Answers
The otiginal price will be the 100% and the sale price will be the 100% minus the 30% so will be the 70%, so with this information we can use a rule of 3 to solve the problem so:
\(\begin{gathered} x\to100 \\ 15.75\to70 \end{gathered}\)so the equation will be:
\(\begin{gathered} x=\frac{100\cdot15.75}{70} \\ x=22.5 \end{gathered}\)!!! CAN SOMEONE HELP !!! (PLEASE ILL GIVE BRAINLIST)

Answers
Answer:
120 minutes
Step-by-step explanation:
the total bill was $58 so we have to subtract the $40 monthly bill part to find how much extra money she paid because her call was over 200 minutes
58-40=18
Then divide the $18 by $0.15 since the $18 is the total amount of each time she was charged $0.15 for going 1 minute over 200 minutes
18÷0.15 = 120
120 is te Amount Of minutes she went over her 200 minute limit
120 minutes
Taylor's total bill was $58 so then i had to subtract the $40 monthly bill part to find how much extra money she paid because her call was over 200 minutes
58-40=18
Then I divide the $18 by $0.15 since the $18 is the total amount of each time she was charged $0.15 for going over 200 minutes
18÷0.15 = 120
120 is the amount of minutes she went over her 200 minute limit
-Millie
I need helppppppppppppp please

Answers
Answer:
I want to say A)
Step-by-step explanation:
Does this table represent a function? Why or why not?

Answers
Answer:
A Yes, because every x value corresponds to exactly one y value
Step-by-step explanation:
A function has a one to one correspondence, or every x goes to only one y value
Since each x goes to only 1 y value this is a function
Answer: It is a function
Step-by-step explanation:
One way to tell if it is a function or not, is to look at the X and Y. While 2 different X values can get the same Y value, one X value should not have 2 different Y values. In the table you can see, there are no repeating X values that have different Y values.
EXAMPLES:
(14, 15)
(13,15)
If these two showed up in a table, it could still be a function
(14, 15)
(14, 16)
If these pairs showed up in a table, than it would not be considered a function
The ages of rocks in an isolated area are known to be approximately normally distributed with a mean of 7 years and a standard deviation of 1.8 years. What percent of rocks are between 5.8 and 7.3 years old?
Answers
Answer: 31.39%
Step-by-step explanation:
Given: The ages of rocks in an isolated area are known to be approximately normally distributed with a mean of 7 years and a standard deviation of 1.8 years.
i.e. \(\mu = 7 \ \ \ \ \sigma= 1.8\)
Let X be the age of rocks in an isolated area .
Then, the probability that rocks are between 5.8 and 7.3 years old :
\(P(5.8<X<7.3)=P(\dfrac{5.8-7}{1.8}<\dfrac{X-\mu}{\sigma}<\dfrac{7.3-7}{1.8})\\\\=P(-0.667<Z<0.167)\ \ \ [z=\dfrac{X-\mu}{\sigma}]\\\\=P(Z<0.167)-P(z<-0.667)\\\\=P(Z<0.167)-(1-P(z<0.667))\\\\=0.5663-(1-0.7476)\\\\=0.3139\)
\(=31.39\%\)
Hence, the percent of rocks are between 5.8 and 7.3 years old = 31.39%
what is -8(4k+2)=112
Answers
Answer:K= -4
Step-by-step explanation:
3. A demand loan of $10,000 is repaid by payments of $5000 in one year, $6000 in four years, and a final payment in six years. Interest on the loan is at 10% per annum compounded quarterly during the first year, 8% per annum compounded semi-annually for the next three years and 7.5% per annum compounded annually for the remaining years. Determine the final payment.A demand loan of $5000.00 is repaid by payments of $2500.00 after two years, $2500.00 after four years, and a final payment after six years. Interest is 9% compounded quarterly for the first two years, 10% compounded monthly for the next two years, and 10% compounded annually thereafter. What is the size of the final payment? The final payment is 5 (Round the final answer to the nearest cent as needed. Round all intermediate values to six decimal places as needed.)
Answers
For the first loan, the final payment is $1,576.25. For the second loan, the final payment is $0. The calculations consider the given interest rates and compounding periods.
To determine the final payment for the first loan, we need to calculate the accumulated value of the loan after six years. For the first year, interest is compounded quarterly at a rate of 10% per annum. The accumulated value after one year is $10,000 * (1 + 0.10/4)^(4*1) = $10,000 * (1 + 0.025)^4 = $10,000 * 1.1038125.For the next three years, interest is compounded semi-annually at a rate of 8% per annum. The accumulated value after four years is $10,000 * (1 + 0.08/2)^(2*4) = $10,000 * (1 + 0.04)^8 = $10,000 * 1.3604877.
Finally, for the remaining two years, interest is compounded annually at a rate of 7.5% per annum. The accumulated value after six years is $10,000 * (1 + 0.075)^2 = $10,000 * 1.157625.To find the final payment, we subtract the payments made so far ($5,000 and $6,000) from the accumulated value after six years: $10,000 * 1.157625 - $5,000 - $6,000 = $1,576.25.For the second loan, we calculate the accumulated value after six years using the given interest rates and compounding periods for each period. The accumulated value after two years is $5,000 * (1 + 0.09/4)^(4*2) = $5,000 * (1 + 0.0225)^8 = $5,000 * 1.208646.
The accumulated value after four years is $5,000 * (1 + 0.10/12)^(12*2) = $5,000 * (1 + 0.0083333)^24 = $5,000 * 1.221494.Finally, the accumulated value after six years is $5,000 * (1 + 0.10)^2 = $5,000 * 1.21.To find the final payment, we subtract the payments made so far ($2,500 and $2,500) from the accumulated value after six years: $5,000 * 1.21 - $2,500 - $2,500 = $0.
To learn more about interest rate click here
brainly.com/question/31520795
#SPJ11
(0, t < 0 5, 0≤t<1. Consider the function f(t) = 3, 1 5 1. Write the function in terms of unit step function f(t) = 0. (Notation: write u(t-c) for the Heaviside step function uc(t) with step at t = c. For example, u5(t) should be entered as u(t - - 5).) 2. Find the Laplace transform of f(t) F(s) = . Find the Laplace transform of F(s) -0 - f(t) = t< 5 (t-5)³, t>5
Answers
The Laplace Transform of f(t) is F(s) = (3 + 5/s) + (1 - 5e^(-s)) / s.
The given function is:
f(t) = 3u(0 - t) + 5u(t - 0)u(1 - t) + u(t - 1)Step 1:To convert f(t) into a unit step function, use the following steps:
For t < 0, the function is zero, so no unit step function is required.
For 0 ≤ t < 1, f(t) = 5. Thus, for this interval, the unit step function is u(t - 0).For t ≥ 1, f(t) = 1.
Thus, for this interval, the unit step function is u(t - 1).
Therefore, f(t) = 3u(0 - t) + 5u(t - 0)u(1 - t) + u(t - 1) = 3u(-t) + 5u(t)u(1 - t) + u(t - 1) Step 2: The Laplace Transform of f(t) is: F(s) = L {f(t)} = L {3u(-t) + 5u(t)u(1 - t) + u(t - 1)} = 3L {u(-t)} + 5L {u(t)u(1 - t)} + L {u(t - 1)}Here, L{u(-t)} = 1/s and L{u(t - 1)} = e^(-s) / s.L {u(t)u(1 - t)} = L {u(t) - u(t - 1)} = L {u(t)} - L {u(t - 1)} = 1/s - e^(-s) / s
Therefore, F(s) = 3L {u(-t)} + 5L {u(t)u(1 - t)} + L {u(t - 1)} = 3 × 1/s + 5 × [1/s - e^(-s) / s] + [e^(-s) / s] = (3 + 5/s) + (1 - 5e^(-s)) / s
Therefore, the Laplace Transform of f(t) is F(s) = (3 + 5/s) + (1 - 5e^(-s)) / s.
to know more about Laplace Transform visit :
https://brainly.com/question/31040475
#SPJ11
The Laplace transform of F(s) - f(t) is given function by \(F(s) - (3 + 5e^{(-s)}) / s = 1 / s^2 - 6 / s^4\).
Writing the function in terms of the unit step function:
f(t) = 3u(t) + 5u(t-1)
The unit step function u(t) is 1 for t ≥ 0 and 0 for t < 0.
The function f(t) is equal to 3 for t ≥ 0 and 5 for 0 ≤ t < 1.
So, we can express f(t) in terms of the unit step function as:
f(t) = 3u(t) + 5u(t-1)
Finding the Laplace transform of f(t):
Using the linearity property of the Laplace transform, we can find the transform of each term separately.
L{3u(t)} = 3 / s (by the Laplace transform property of u(t))
\(L\ {5u(t-1)} = 5e^{(-s)} / s\) (by the Laplace transform property of u(t-a))
Therefore, the Laplace transform of f(t) is given by:
\(F(s) = L{f(t)} = 3 / s + 5e^{(-s)} / s\)
Alternatively, we can combine the terms:
\(F(s) = 3 / s + 5e^{(-s)} / s\)
\(= (3 + 5e^{(-s)}) / s\)
So, the Laplace transform of f(t) is \(F(s) = (3 + 5e^{(-s)}) / s\).
Finding the Laplace transform of F(s) - f(t):
We are given F(s) - f(t) = t < 5 (t - 5)³, t > 5.
Using the Laplace transform properties, we can find the transform of each term.
L{t} = 1 / s² (by the Laplace transform property of t^n)
L{(t - 5)³} = 6 / s⁴ (by the Laplace transform property of (t-a)ⁿ)
Therefore, the Laplace transform of F(s) - f(t) is given by:
L{F(s) - f(t)} = L{(t < 5) (t - 5)³, (t > 5)}
= 1 / s² - 6 / s⁴
So, the Laplace transform of F(s) - f(t) is given by \(F(s) - (3 + 5e^{(-s)}) / s\) = 1 / s² - 6 / s⁴.
To know more about Laplace transform, visit:
https://brainly.com/question/30759963
#SPJ11
a client who weighs 70 kg is receiving a solution of 0.9% sodium chloride (normal saline) 500 ml with dopamine 800 mg at 5 ml/hour. how many mcg/kg/minute is the client receiving? (enter the numeric value only. if rounding is required, round to the nearest tenth.)
Answers
1.904 mcg/kg/min is what the client receives.
The number of mcg/kg/minute = flow rate × concentration ÷ mass of client
Flow rate = 12 ml/ hour = 12 /60 = 1/5 = 0.2 ml/min
Formula:
Concentration = mass of dopamine/volume
mass of dopamine = 800mg
volume = 500ml
Concentration = 800/ 500
= 1.6 mg/ml
= 1.6 × 1000 mcg/mg
= 1600 mcg/mg
Here the mass of the client = 70kg
Now calculating mcg/kg/minute = flow rate× concentration÷ mass of client
= 0.08 ml/min × 1600mcg/ml ÷70 kg
= 320/70
= 1.904 mcg/kg/min
Therefore mcg/kg/min is 1.904.
To know more about the mcg/kg/min refer to the link given below:
https://brainly.com/question/17355009
#SPJ4
3. Given the following table find the slope 2 6 8 Time (hours) Distance (miles) 3 6 9 12

Answers
Answer:
3/2
Step-by-step explanation:
when you plot it time is x and distance is y so go up 3 right 2
What is the equation of the line that passes through the point (7,2) and has a slope of 1
Answers
Answer:
y=x-5
Step-by-step explanation:
For this, use point-slope formula, which is (y-y1)=k(x-x1), in which k is slope.
Now, substitute in your values. (y-2)=1(x-7)
Then, since you got y-2=x-7, add 2 to both sides.
You get y=x-5
y = x +5 is the equation of the line that passes through the point (7,2) and has a slope of 1.
What is an equation of a line?The equation of a straight line is y=mx+c where m is the gradient and c is the height at which the line crosses the y -axis, also known as the y-intercept. There are three major forms of linear equations: point-slope form, standard form, and slope-intercept form.
given, a line that passes through the point (7,2) and has a slope of 1
Since the Slope of the line = 1
From the slope-intercept form of the line
y = mx + c
thus, the Equation of the line
y = 1 * x + c
y = x + c
Since this line passes through coordinates (7, 2 ) this point will satisfy the equation
7 = 2 + c
c = 5
hence, the equation of a line
y = x +5
therefore, the equation of the line that passes through the point (7,2) and has a slope of 1 is y = x +5.
Learn more about the equation of line here:
https://brainly.com/question/21511618
#SPJ3
a. find the 30th percentile for the standard normal distribution b. find the 30th percentile for a normal distribution with mean 10 and std. dev. 1.5
Answers
a. To find the 30th percentile for the standard normal distribution, we first need to locate the z-score that corresponds to this percentile. We can use a standard normal distribution table or a calculator to find this value. From the table, we can see that the z-score that corresponds to the 30th percentile is approximately -0.524. Therefore, the 30th percentile for the standard normal distribution is z = -0.524.
b. To find the 30th percentile for a normal distribution with mean 10 and standard deviation 1.5, we can use the formula for transforming a standard normal distribution to a normal distribution with a given mean and standard deviation. This formula is:
z = (x - μ) / σ
where z is the standard normal score, x is the raw score, μ is the mean, and σ is the standard deviation.
To find the 30th percentile for this distribution, we first need to find the corresponding z-score using the formula above:
-0.524 = (x - 10) / 1.5
Multiplying both sides by 1.5, we get:
-0.786 = x - 10
Adding 10 to both sides, we get:
x = 9.214
Therefore, the 30th percentile for a normal distribution with mean 10 and standard deviation 1.5 is x = 9.214. This means that 30% of the observations in this distribution are below 9.214.
Learn more about z-score here
https://brainly.com/question/28000192
#SPJ11
In the diagram below, \overline{OP} OP is parallel to \overline{LM} LM . Solve for xx. Round your answer to the nearest tenth if necessary and the numbers on the diagram are 14.2,13.3,10.7
Answers
The value of x from the given diagram is approximately 17.7
Similarity theorem of a triangleApplying this theorem to the given triangle, we will have:
x/x+14.2 = 13.3/13.3+10.7
x/x+14.2 = 13.3/24
x/x+14.2 =0.55416
x = 0.55416(x+14.2)
x - 0.55416x = 7.8692
0.44584x = 7.8692
x = 17.7
Hence the value of x from the given diagram is approximately 17.7
Learn more on similar triangles here: https://brainly.com/question/2644832

Triangle ABC is graphed in the coordinate plane.

Answers
Answer:
the answer is d
Step-by-step explanation:
just see the matching coordinates
A textbook store sold a combined total of 375 chemistry and sociology textbooks in a week. The number of chemistry textbooks sold was two times the number of sociology textbooks sold. How many textbooks of each type were sold?
Answers
The bookstore sold a total of 150 chemistry textbooks and 225 sociology textbooks.
What is a linear equation in two variables?
An equation is said to be a linear equation in two variables if it is written in the form of ax + by + c=0, where a, b & c are real numbers and the coefficients of x and y, i.e a and b respectively, are not equal to zero.
Let C be the number of chemistry textbooks sold and S be the number of sociology textbooks sold. We can write the following system of equations to represent the given information:
C + S = 375
C = 2S
To solve this system of equations, we can substitute the second equation into the first equation to get C + 2S = 375. Then we can solve for S by subtracting C from both sides to get 3S = 375 - C. Dividing both sides by 3 gives us S = (375 - C) / 3.
Substituting this expression for S back into the second equation, we get C = 2((375 - C) / 3). Multiplying both sides by 3 and simplifying gives us 3C = 750 - 2C, or C = 750 / 5 = 150.
Substituting this value for C back into the first equation, we get 150 + S = 375, so S = 375 - 150 = 225.
Hence, the bookstore sold a total of 150 chemistry textbooks and 225 sociology textbooks.
To learn more about linear equations in two variables, visit:
brainly.com/question/13951177
#SPJ1
please help i will give 20 points for both answers
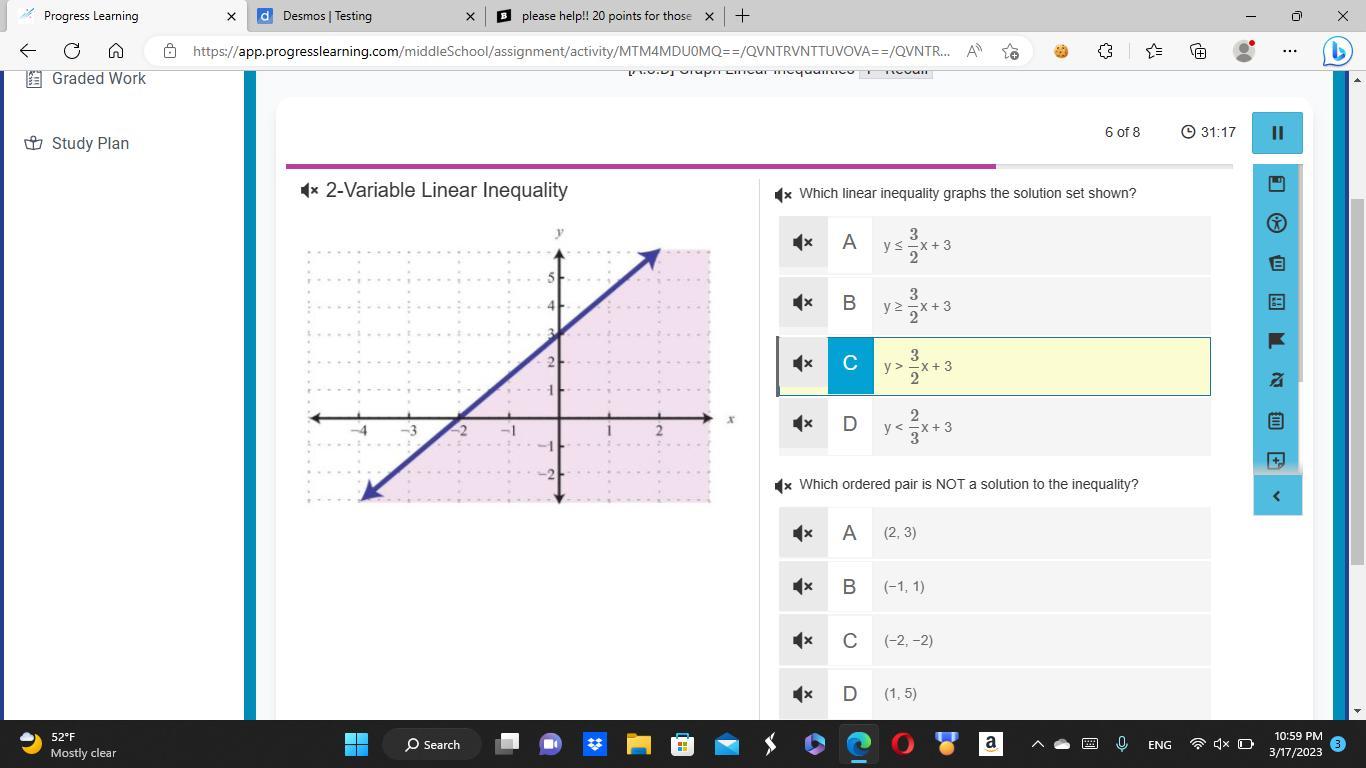
Answers
Answer:
1. A - \(y\leq \frac{3}{2} x+3\)
2. D - (1,5)
Step-by-step explanation:
The equation \(y\leq \frac{3}{2} x+3\) fits this graph.
y has to be less than x due to the shaded part of the graph being on the underside of the line
To confirm this we can plug in a value to see if the inequality is true
I will use the origin as an example:
\(0\leq \frac{3}{2} (0)+3\)
\(0\leq 3\)
This inequality is true meaning this point is in the shaded region of the graph
Also the equation has to have an equal to because it has a solid line and not a dotted line
The point that isn't a solution is (1,5) due to the fact it isn't in the shaded region and when plugged into the equation gives a false inequality
\(5\leq \frac{3}{2} (1)+3\)
\(5\leq \frac{3}{2}+3\)
\(\frac{10}{2} \leq \frac{9}{2}\)
This inequality is false which means the point (1,5) isn't a solution to this equation.
Answer:
1.) A
2.) D
Step-by-step explanation:
1.) find equation of line:
b=3, m=1.5
y=1.5x+3
shaded is below therefore
y\(\leq\)1.5x+3
*line under inequality because line is solid
2.) (1,5) is not a solution because it is above shaded figure
Evaluate the integral: S1 0 (-x³ - 2x² - x + 3)dx
Answers
The integral: S1 0 (-x³ - 2x² - x + 3)dx is -1/12
An integral is a mathematical operation that calculates the area under a curve or the value of a function at a specific point. It is denoted by the symbol ∫ and is used in calculus to find the total amount of change over an interval.
To evaluate the integral:
\($ \int_0^1 (-x^3 - 2x^2 - x + 3)dx $\)
We can integrate each term of the polynomial separately using the power rule of integration, which states that:
\($ \int x^n dx = \frac{x^{n+1}}{n+1} + C $\)
where C is the constant of integration.
So, we have:
\($ \int_0^1 (-x^3 - 2x^2 - x + 3)dx = \left[-\frac{x^4}{4} - \frac{2x^3}{3} - \frac{x^2}{2} + 3x\right]_0^1 $\)
Now we can substitute the upper limit of integration (1) into the expression, and then subtract the result of substituting the lower limit of integration (0):
\($ \left[-\frac{1^4}{4} - \frac{2(1^3)}{3} - \frac{1^2}{2} + 3(1)\right] - \left[-\frac{0^4}{4} - \frac{2(0^3)}{3} - \frac{0^2}{2} + 3(0)\right] $\)
Simplifying:
\($ = \left[-\frac{1}{4} - \frac{2}{3} - \frac{1}{2} + 3\right] - \left[0\right] $\)
\($ = -\frac{1}{12} $\)
Therefore,
\($ \int_0^1 (-x^3 - 2x^2 - x + 3)dx = -\frac{1}{12} $\)
To learn more about substituting visit:
https://brainly.com/question/10423146
#SPJ11
Subtract -9x² - x + 9 from 8x² - 6x - 8.
Answers
Answer:
17x^2-5x-17
Step-by-step explanation:
(8x^2-6x-8)-(-9x^2-x+9)
8x^2-6x-8+9x^2+x-9
17x^2-5x-17
determine the set of points at which the function is continuous. f(x, y) = xy 8 ex − y
Answers
The set of points at which the function f(x, y) = xy/(8ex − y) is continuous is the set of all points (x, y) such that 8ex ≠ y.
How we find the set of points where the function f(x, y) = xy\(^8ex\) - y is continuous.To determine the set of points at which the function is continuous, we need to check if the limit of the function exists and is equal to the value of the function at that point.
Taking the limit of the function as (x,y) approaches (a,b) gives:
lim_(x,y)→(a,b) f(x,y) = lim_(x,y)→(a,b) xy/8ex-y
Using L'Hopital's rule, we can find that the limit is equal to \(ab/8e^(b-a)\).
The function is continuous for all points (a,b) in \(R^2\).
Learn more about set of points
brainly.com/question/7876320
#SPJ11
It is given that A⃗ −B⃗ =(−51.4m)x^,C⃗ =(62.2m)x^, and A⃗ +B⃗ +C⃗ =(13.8m)x^.
Find the vector A⃗ . Find the vector B⃗ .
Answers
The vector A is (49.9m) x and vector B is (1.5m) x.
In the given question, A − B = (−51.4m)x, C =(62.2m)x, and A +B +C =(13.8m)x.
Find the vector A. Find the vector B.
We may disregard the vector x and treat the issue as an arithmetic one since all of the measurements are in the same direction (simultaneous equations).
A − B = −51.4.............................(1)
C = 62.2.............................(2)
A + B + C = 13.8.............................(3)
Now putting the value of C from Equation (2) in Equation (3)
A + B + C = 13.8
A + B + 62.2 = 13.8
Subtract 62.2 on both side, we get
A + B = 13.8 - 62.2
A + B = - 48.4.....................(4)
Adding the equation (1) and (4), we get
2A = - 99.8
Divide by 2 on both side, we get
A = - 49.9
Now subtracting the equation (1) and (4), we get
2B = -48.4 - ( -51.4)
2B = 3
Divide by 2 on both side, we get
B = 1.5
Since all of the calculations are done in terms of the unit vector x.
So the answer is vector B = (1.5m) x and vector A = (49.9m) x.
To learn more about vector link is here
brainly.com/question/29740341
#SPJ4
what is the middle splitting term
Answers
Answer:
In Quadratic Factorization using Splitting of Middle Term which is x term is the sum of two factors and product equal to last term. To Factor the form :ax 2 + bx + c. Factor : 6x 2 + 19x + 10. 1) Find the product of 1st and last term( a x c).
Step-by-step explanation:
I hope that helped you!! sorry if not!!
Find the Slope m of the line that passes through the pair of points ( -4 , 4 ) and ( -4 , 0 ).
Answers
In an equation it would be 0.5x
Please answer correctly !!!!!!! Will mark Brianliest !!!!!!!!!!!!!!!!

Answers
Answer:
8 5 5
Step-by-step explanation:
Line 3 sets t = 5
Line 5 sets n = t = 5
Line 6 sets c = n+3 = 8
The displayed values for c, n, are
8 5 5
Consider the equation 7=3x-5.
a. Stanley wants to start solving the equation by adding 5 to both sides, while Terrence first wants to subtract 7 from both sides. Will both strategies work? Is one strategy more efficient than the other?
b. Solve 7=3x-5. Show your steps.
Answers
We can answer the two questions by relying on our knowledge of how to solve equations, showing how both strategies are efficient, and finding x.
a. Both strategies will work and lead to the same solution. It's just a matter of personal preference which one to use. However, subtracting 7 from both sides may be more efficient in this case because it eliminates the need for an extra step of adding 5 to both sides.
b. TStarting with 7 = 3x - 5, we can add 5 to both sides to get:
7 + 5 = 3x - 5 + 5
12 = 3x
12/3 = 3x/3
4 = x
How to solve equationsTo solve an equation, you need to find the value of the variable that makes the equation true. The following steps can be used to solve most equations:
Simplify both sides of the equation. Combine like terms and use the distributive property to remove parentheses.Isolate the variable term. Move all the terms that do not have the variable to the other side of the equation.Solve for the variable. Use inverse operations to isolate the variable term. For example, if the variable is multiplied by a constant, divide both sides of the equation by that constant. If the variable is added to or subtracted from a constant, use the opposite operation to cancel out that constant.Check your solution. Substitute the value you found for the variable back into the original equation to make sure it makes the equation true.It's important to remember that whatever you do to one side of the equation, you must also do to the other side to maintain the equality. Additionally, if the equation has parentheses, use the distributive property to simplify the expression inside the parentheses.
Some equations may have special cases, such as quadratic equations or equations with absolute values. These types of equations may require additional steps and methods to solve.
Learn more about equations here:
https://brainly.com/question/2972832
#SPJ1
PLEASE ANSWER FAST I WILL GIVE BRAINLIEST

Answers
Answer:
Here are the answers, in order:
dependent, the same amount, independent
dependent, a different amount, independent
i’m taking a test
hello
f r eee e e e
poI nT s
my last account got B A N N E D

Answers
Answer:
yayz fwee pwoints thwank ywuo
Step-by-step explanation:
