Phosphorus -32 is a radioisotope with a half -life of 14.3 days. If you start with 4.0g of phosphorus -32, how many grams will remain after 57.2 days? How many half -lives will have passed? Hint: first determine how many ( 1)/(2) lives
Answers
To determine the amount of phosphorus-32 remaining after 57.2 days, we need to calculate how many half-lives have passed.
The number of half-lives can be found by dividing the total time elapsed (57.2 days) by the half-life (14.3 days):
Number of half-lives = (Total time elapsed) / (Half-life) = 57.2 days / 14.3 days = 4
Since each half-life reduces the amount of phosphorus-32 by half, after 4 half-lives, the remaining amount is (1/2)^4 = 1/16 of the original amount.
The remaining amount of phosphorus-32 after 57.2 days is:
Remaining amount = (1/16) * (Original amount) = (1/16) * 4.0g = 0.25g
Therefore, after 57.2 days, 0.25 grams of phosphorus-32 will remain, and 4 half-lives will have passed.
To learn more about phosphorus
brainly.com/question/31606194
#SPJ11
Related Questions
Consider the partial differential equation + کے تحت subject to the boundary conditions uço, t) = u(1, t) = 0,t> 0 Separating variables by writing u(x, t) = X(x)T(t), determine the ordinary differential equation satisfied by T(t), that involves a positive constant k2. Determine the ordinary differential equation in the form T"(t) + ak2T(t) = 0. Hence input the value of a.
Answers
The ordinary differential equation satisfied by T(t) is:
T''(t) + k²T(t) = 0
with a = 1.
We have,
To separate variables in the given partial differential equation, we assume that the solution can be written as a product of functions:
u(x, t) = X(x)T(t)
Substituting this into the partial differential equation, we have:
X''(x)T(t) + X(x)T''(t) = 0
Dividing the equation by X(x)T(t), we get:
X''(x)/X(x) + T''(t)/T(t) = 0
Since the left side of the equation depends only on x and the right side depends only on t, both sides must be constant.
Let's denote this constant by -k², where k is a positive constant:
X''(x)/X(x) = -k²
This gives us the ordinary differential equation for X(x):
X''(x) + k²X(x) = 0
Now, let's focus on the ordinary differential equation for T(t). We have:
T''(t)/T(t) = k²
Rearranging the equation, we obtain:
T''(t) + k²T(t) = 0
Comparing this equation with the desired form T''(t) + ak²T(t) = 0, we see that a = 1.
Therefore,
The ordinary differential equation satisfied by T(t) is:
T''(t) + k²T(t) = 0
with a = 1.
Learn more about partial derivatives here:
https://brainly.com/question/28751547
#SPJ4

The data life cycle has six stages, whereas data analysis has six _____.
Answers
The six stages of the data life cycle are complemented by six stages in data analysis, which involve various processes to extract insights and meaning from data.
Data analysis is a crucial component of the data life cycle, focusing on extracting valuable insights and meaning from collected data. The six stages of data analysis can be summarized as follows:
1. Data Exploration: This stage involves understanding the data, identifying patterns, and exploring its characteristics. It includes tasks such as data cleaning, data transformation, and initial data visualization.
2. Data Preparation: In this stage, data is prepared for analysis by selecting relevant variables, transforming data into a suitable format, and handling missing values or outliers. It aims to ensure data quality and consistency.
3. Data Modeling: Here, various statistical and machine learning techniques are applied to develop models that represent relationships within the data. This stage includes selecting appropriate models, training them on the data, and validating their performance.
4. Data Evaluation: The models and results obtained from the previous stage are evaluated to assess their accuracy, reliability, and suitability for the given problem. Evaluation metrics and techniques are employed to measure the performance of the models.
5. Data Interpretation: This stage involves interpreting the results of the analysis to extract meaningful insights and draw conclusions. It requires domain knowledge and expertise to understand the implications of the findings and their impact on decision-making.
6. Data Presentation: Finally, the insights and conclusions derived from the analysis are communicated effectively to stakeholders. This stage involves creating visualizations, reports, and presentations that convey the results in a clear and understandable manner.
By following these six stages of data analysis, organizations can derive actionable insights, make informed decisions, and drive improvements based on the findings from the data life cycle.
Learn more about Data analysis here:
https://brainly.com/question/28840430
#SPJ11
How do you construct a line segment that is 1/3 the length of the given line segment?
Answers
To steps to construct a line segment that is 1/3 the length of the given segment is:
Draw a line segment CD of any length.Fix the compass's end on C and pencil on D. This gives the length of CD.Now divide the length of CD by 3. That is the 1/3 the length of CD.Draw a line 1. Mark a point A on line 1. Change compass's setting into 1/3 the length of CD, place the compass at A.Make an arc on the line l which cuts l at B. Now, AB is a copy of CD which is 1/3 the length of CD.What is line segment?A line segment is bounded by two definite points on a line. We also can say a line segment is part of the line which connects two points. A line has no endpoints and extends immensely in both the direction but a line segment has two fixed or distinct endpoints.
Learn more about line segment at: https://brainly.com/question/30072605
#SPJ4
A car dealership sells cars that were made in 2015 through 2020. Let the cars for sale be the domain of a relation R where two cars are related if they were made in the same year. (a) Prove that this relation is an equivalence relation. (b) Describe the partition defined by the equivalence classes.
Answers
The given relation obeys reflexive, symmetric, and transitive properties, therefore, it is in relation to equivalence relation.
How is the equivalence relation depicted?Let the domain of the relation is car(x) belongs to 2015 , 2016, 2017, 2018, 2019, 2020
To prove equivalence relation, we need to prove reflexive, symmetric, transitive properties.
Reflexive relation: x is related to x
Here car(x) is made in 2015, so, car(x)) is in R where R is reflexive relation.
Symmetric relation: x is related to y implies y is related to x
Here (car(x) , car(y)) is in R , i.e car(x) and car(y) are made in same year. R obeys symmetric property
Transitive property: x is related to y and y is related to z then x is related to z. Here (car(x),car(y)), (car(y), car(z)) is in R. Therefore (car(x) , car(z)) is in R
Therefore, the given relation obeys reflexive, symmetric, and transitive properties, therefore, it is in relation to equivalence relation.
B. The cars which are made in the same year are in one equivalence class all cars are made in overall 6 years. We get 6 equivalence classes. These classes are partitions, so we have six partitions
Learn more about relations on:
https://brainly.com/question/1579288
The ratio of oranges sold to bananas sold is 3 to 10. If a total of 30 bananas were sold,then how many oranges were sold ?
Answers
Answer:
9
Each value is 3 times the number on the ratio.
10 x 3 = 30.
So, the ratio for oranges would be 9 because:
3 x 3 = 9.
So, the answer is 9.
Find the equation of the line that goes through the points (4, 4) and (8, 6).
y = 1/2 x + 2
y = 4x + 6
y = 1/2 x + 4
y = 2x - 4
Answers
Answer:
A
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
Some spiders can spin a web at 3 cm per second. Convert this rate to meters per minute. (100 cm = 1 m)
Answers
Answer:
1.8m per minute
Step-by-step explanation:
Answer:
\(\frac{1.8 \ m}{1 \ min}\) ; (1.8 meters per minute)
Step-by-step explanation:
Use dimensional analysis to solve this problem.
The proper units of conversion are given in parentheses on this question: 100 cm = 1 m.
Start with the given value, 3 centimeters/1 second.
\(\frac{3 \ cm}{1\ sec}\)Convert this rate to meters/minute by multiplying 3 cm/1 sec by 1 m/100 cm.
\(\frac{3 \ cm}{1 \ sec} * \frac{1 \ m}{100 \ cm}\)The top and bottom units should cancel out, so that's how you know to put the cm units on the bottom to cancel out with the 3 cm on the top.
Multiply the fractions together. The "cm" units cancel out.
\(\frac{3\ m}{100 \ sec}\)Now you want to make the bottom units = minutes. There are 60 seconds in 1 minute, so you can use \(\frac{60 \ sec}{1 \ min}\) to multiply with \(\frac{3\ m}{100 \ sec}\).
\(\frac{3\ m}{100 \ sec} * \frac{60 \ sec}{1 \ min}\)The "seconds" unit cancels out, so you are left with meters on the top and minutes on the bottom. Multiply the fractions together.
\(\frac{180 \ m}{100 \ min}\)We want the rate to be meters per minute (1), so completely simplify this fraction and divide the fraction by (100/100), so the denominator is 1 min.
\(\frac{180 \ m}{100 \ min} \div \frac{100}{100}= \frac{1.8 \ m}{1 \ min}\)scenario 6-3 in a certain population of students, the number of calculators a student owns is a random variable x described by the following probability distribution: x 0 1 2 p(x) 0.2 0.6 0.2 use scenario 6-3. which of the following is the mean of x? group of answer choices 1 the answer cannot be computed from the information given. 2 0.5 1.2 next
Answers
1.0 is the mean of the variable x
How to find the mean of x?
The mean or expected value is defined as the predicted value of a variable, calculated as the sum of all possible values each multiplied by the probability of its occurrence.
Given :
x| 0 1 2
p| 0.2 0.6 0.2
The expected value of x, E(x) =Σ xp
where x = number of classes and p = probability
E(x) = (0×0.2) + (1×0.6) + (2×0.2)
E(x) = 0 + 0.6 + 0.4
E(x) = 1.0
Therefore, the mean of the variable x is 1.0
Learn more expected value on:
brainly.com/question/29352440
#SPJ1
the local newspaper claims the 15 percent of the residents in its community play the state lottery, if you plan to test the claim by taking a random sample from the community, the appropraite set hypothesies is
Answers
The appropriate set of hypothesis is:
Null hypothesis (H0): The proportion of residents in the community who play the state lottery is equal to 15%.
Alternate hypothesis (Ha): The proportion of residents in the community who play the state lottery is not equal to 15%.
To test the claim made by the local newspaper, you would need to set up a hypothesis. The appropriate set of hypotheses in this case would be:
Null hypothesis (H0): The proportion of residents in the community who play the state lottery is equal to 15%.
Alternate hypothesis (Ha): The proportion of residents in the community who play the state lottery is not equal to 15%.
By setting up these hypotheses, you can then collect a random sample from the community and analyze the data to determine if there is enough evidence to support the claim made by the newspaper.
Let us know more about hypothesis : https://brainly.com/question/31319397.
#SPJ11
What is the maximum of thisgraph over the interval [-4, 4]?
Answers
The maximum of a graph is found on the y axis. Considering the given interval, the point on the y axis is 4. Thus, the maximum of the graph over the interval is 4.
I need help on three questions. I hope it doesn't take up a lot of time.
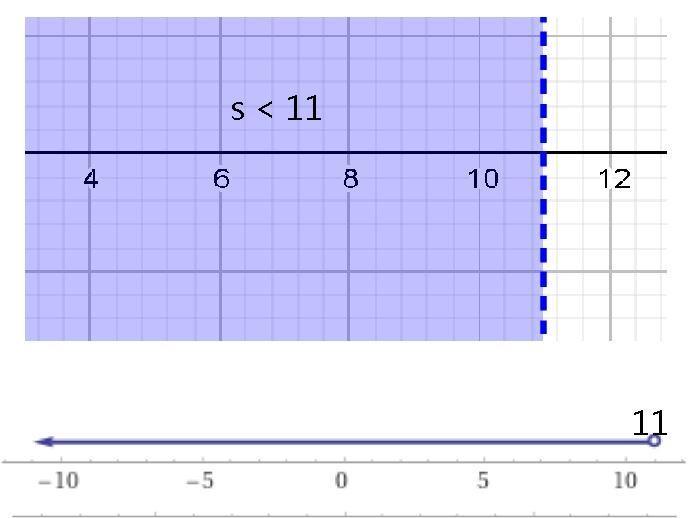
1) Solve x+9−3≤14. Graph the solution.
2)Solve 44>7+s+26. Graph the solution.
3Solve 6.1−0.3≥c+1. Graph the solution.
Thank you if you answer these i will mark your answer Brainliest.
Answers
Answer:
1) x ≤ 8
2) s < 11
3) c ≤ 4.8
Step-by-step explanation:
1) x+9-3≤14
x+6≤14
x ≤ 8
2) 44>7+s+26
44>33+s
s < 44-33
s <11
3) 6.1 - 0.3 ≥ c + 1
5.8 ≥ c + 1
c ≤ 4.8


a correlation score of 0.75 between two variables such as symptoms of anxiety and symptoms of depression indicates what kind of relationship between these variables?
Answers
A correlation score of 0.75 between two variables such as symptoms of anxiety and symptoms of depression indicates a strong positive relationship between these variables.
This means that as the level of symptoms of anxiety increase, there is a high likelihood that the level of symptoms of depression will also increase. Conversely, as the level of symptoms of anxiety decreases, the level of symptoms of depression is likely to decrease as well.
It's important to note that correlation does not imply causation, meaning that just because there is a strong positive correlation between two variables, it doesn't necessarily mean that one variable causes the other. Further research would be needed to establish any causal relationship between symptoms of anxiety and symptoms of depression.
Know more about correlation here:
https://brainly.com/question/13879362
#SPJ11
Please give the proof process: 2n3 + 3n +10 = Q( n³).
Answers
2n^3 + 3n + 10 can be written as a polynomial of the form Q(n^3), where Q(n^3) represents the set of polynomials of the form a(n^3).
To prove that the expression 2n^3 + 3n + 10 is in the set Q(n^3), where Q(n^3) represents the set of polynomials of the form a(n^3), we need to show that the expression can be written in the form a(n^3) for some constant "a".
Let's start by factoring out the common factor of n^3 from each term:
2n^3 + 3n + 10 = n^3(2 + 3/n^2 + 10/n^3)
Now, let's rewrite the expression as a single term multiplied by n^3:
2n^3 + 3n + 10 = (2 + 3/n^2 + 10/n^3)n^3
Simplifying the expression inside the parentheses:
= (2n^3 + 3n^2 + 10n^3)/n^3
= (12n^3 + 3n^2)/n^3
= 12 + 3/n
ow, we can see that the expression can be written in the form a(n^3), where a = 12 and n^3 = 3/n.
Therefore, we have shown that 2n^3 + 3n + 10 can be written as a polynomial of the form Q(n^3), where Q(n^3) represents the set of polynomials of the form a(n^3).
Learn more about polynomial here
https://brainly.com/question/30478639
#SPJ11
problem 5 (30 points, each 10 points). in a chemical plant, 24 holding tanks are used for final product storage. four tanks are selected at random and without replacement. suppose that four of the tanks contain material in which the viscosity exceeds the customer requirements. 1. what is the probability that exactly one tank in the sample contains high-viscosity material? 2. what is the probability that at least one tank in the sample contains high-viscosity material? 3. in addition to the four tanks with high-viscosity levels, four different tanks contain material with high impurities. what is the probability that exactly one tank in the sample contains high-viscosity material and exactly one tank in the sample contains material with high impurities?
Answers
1. The probability of selecting exactly one tank with high-viscosity material is 0.
2. The probability of selecting at least one tank with high-viscosity material is 1.
3. The probability of selecting exactly one tank with high-viscosity material and exactly one tank with high impurities is 0.25.
1. The probability of selecting exactly one tank with high-viscosity material is calculated by the binomial distribution formula, P(X = n) = (nCx)p^x(1-p)^n-x, where n is the number of trials, x is the number of successes, and p is the probability of success. In this case, n = 4, x = 1, and p = 24/24 = 1. Therefore, P(X = 1) = (4C1)1^1(1-1)^4-1 = 0.
2. The probability of selecting at least one tank with high-viscosity material is calculated by the complement rule, P(X > 0) = 1 - P(X = 0). In this case, P(X > 0) = 1 - (4C0)1^0(1-1)^4-0 = 1.
3. The probability of selecting exactly one tank with high-viscosity material and exactly one tank with high impurities is calculated by the binomial distribution formula, P(X = n) = (nCx)p^x(1-p)^n-x, where n is the number of trials, x is the number of successes, and p is the probability of success. In this case, n = 8, x = 2, and p = 24/24 = 1. Therefore, P(X = 2) = (8C2)1^2(1-1)^8-2 = 0.25.
Learn more about probability here:
https://brainly.com/question/14206287
#SPJ4
Complete the grouped relative frequency distribution for the data. Write each relative frequency as a decimal rounded to the nearest hundredth.( note that we are using a class width of 5)

Answers
Relative frequency can be defined as the number of times an event occurs divided by the total number of events occurring in a given scenario. The formula is given to be:
\(RF=\frac{f}{n}\)where f is the number of times the data occurred and n is the total number of observations.
We have the frequency of the individual groups as shown below:
\(\begin{gathered} 1\text{ to }5\Rightarrow3 \\ 6\text{ to }10\Rightarrow8 \\ 11\text{ to }15\Rightarrow3 \\ 16\text{ to }20\Rightarrow5 \end{gathered}\)The total number of observations is 19.
Therefore, the relative frequencies are calculated below:
\(\begin{gathered} 1\text{ to }5\Rightarrow\frac{3}{19}=0.16 \\ 6\text{ to }10\Rightarrow\frac{8}{19}=0.42 \\ 11\text{ to }15\Rightarrow\frac{3}{19}=0.16 \\ 16\text{ to }20\Rightarrow\frac{5}{19}=0.26 \end{gathered}\)ANSWER
\(\begin{gathered} 1\text{ to }5\Rightarrow0.16 \\ 6\text{ to }10\Rightarrow0.42 \\ 11\text{ to }15\Rightarrow0.16 \\ 16\text{ to }20\Rightarrow0.26 \end{gathered}\)T
Express as a simple fraction in lowest terms
OK

Answers
Answer:
1/3
Step-by-step explanation:
First find the LCD or least common denominator. The least common denominator is the number that both of the denominators are divisible by.
In this case, 2 and 3 are both divisible by 6.
Convert both fractions into a fraction with a denominator of 6.
1/2 = 3/6 (multiply numerator and denominator by 3)
2/3 = 4/6 (multiply numerator and denominator by 2)
Now you can multiply as they have the same denominator.
3/6 × 4/6 = 12/36
Simplify.
12/36 = 1/3 (numerator and denominator are divisible by 12)
Hope that helps.
Martha likes to knit hats and mittens for friends and family. Last fall, she knitted 3 hats and 3
pairs of mittens, which took a total of 51 hours. This fall, she knitted 3 hats and 5 pairs of
mittens, which took a total of 77 hours. If each hat takes the same amount of time and each
pair of mittens takes the same time, how long does it take Martha to knit each item?
hours to knit a pair of mittens.
It takes Martha
hours to knit a hat and
Answers
It takes Martha `4` hours to knit each hat and `13` hours to knit each pair of mittens.
What is meant by hours?
Hours are a unit of time used to measure the duration of an event or activity. An hour is equal to 60 minutes or 3,600 seconds. It is often used to indicate the time of day or to schedule appointments or events.
What is a pair?
A pair is a set of two things that go together or belong together, like a pair of shoes, socks, or gloves. It can also refer to a pair, a duo, or a twosome.
According to the given question
Let's assume that each hat takes `h` hours to knit and each pair of mittens takes `m` hours to knit.
From the given information, we know that:
- 3 hats and 3 pairs of mittens took a total of 51 hours. This means that 3h + 3m = 51.
- 3 hats and 5 pairs of mittens took a total of 77 hours. This means that 3h + 5m = 77.
We can use these two equations to solve for `h` and `m`.
First, let's solve for `h` by multiplying the first equation by 5 and the second equation by 3, and then subtracting the second equation from the first:
15h + 15m = 255
9h + 15m = 231
-----------------
6h = 24
h = 4
So each hat takes Martha `4` hours to knit.
Now we can use either of the original equations to solve for `m`. Let's use the first one:
3h + 3m = 51
3(4) + 3m = 51
12 + 3m = 51
3m = 39
m = 13
So each pair of mittens takes Martha `13` hours to knit.
To know more about hours visit
brainly.com/question/13533620
#SPJ1
PLEASE HELPPPPPPP ME

Answers
Answer:
12.56Step-by-step explanation:
To get the length of the arc, we are going to use the formula for calculating the circumference of a semicircle.
Circumference of a semi circle = πd/2
Given
Diameter d = 8
π = 3.14
Substitute;
C = 3.14(8)/2
C = 3.14 * 4
C = 12.56
Hence the the length of the arc is 12.56
please help me with this problem!!

Answers
The details which describe the free African American who lived in the South is that they were counted as part of population statistics which is denoted as option D.
What is Population statistics?This is referred to an an entire set of items from which you draw data for a statistical study while on the other hand, population refers to the people who live in a particular area at a specific time.
From the passage we were told that there was about 225,964 free African americans of which only 6 percent were free black people which made them less than those found in the North. They were counted during census which means that they were part of the population statistics.
Read more about Population statistics here https://brainly.com/question/29885716
#SPJ1
The length of a rectangle is 5 ft longer than its width.
If the perimeter of the rectangle is 70 ft, find its length and width.
Answers
Answer:
Length 20
Width 15
Step-by-step explanation:
what is the percent decrease from 6,000 to 900
Answers
Answer:
85%
Step-by-step explanation:
900-6000 divided by 6000
multiply your answer by 100
that will give you your answer
Let m(t)=(1/6)et + (2/6)e2t + (3/6)e3t. Find the following:
a) E(Y)
b) V(Y)
c) The distribution of Y.
Answers
a)E(Y) = (1/6) × 0 + (2/6) ∞ + (3/6) ∞= ∞Thus, E(Y) is infinity.
b)The variance of the given random variable V(Y) = ∞ - ∞2= ∞Thus, V(Y) is infinity.
c)This means that the distribution of Y is a mixture of three exponential distributions with parameters 1, 2, and 3.
E(Y)The given random variable can be expressed in the form of:m(t) = (1/6) et + (2/6) e2t + (3/6) e3tTherefore, we can obtain the expected value of Y as:E(Y) = (1/6) E(et) + (2/6) E(e2t) + (3/6) E(e3t)Using the formula of the expected value of et, we have:E(et) = ∫et × et dx from 0 to ∞ = [et/2] from 0 to ∞ = 0, so E(et) = 0Now,E(Y) = (1/6) × 0 + (2/6) E(e2t) + (3/6) E(e3t)Again, we use the expected value formula, but this time we apply it to e2t and e3t. We have:E(e2t) = ∫e2t × e2t dx from 0 to ∞ = [e4t/4] from 0 to ∞ = ∞, so E(e2t) = ∞E(e3t) = ∫e3t × e3t dx from 0 to ∞ = [e6t/6] from 0 to ∞ = ∞, so E(e3t) = ∞Therefore,E(Y) = (1/6) × 0 + (2/6) ∞ + (3/6) ∞= ∞Thus, E(Y) is infinity.
V(Y)The variance of the given random variable can be expressed in the form of:V(Y) = E(Y2) - [E(Y)]2To calculate the variance, we need to find the expected value of Y2. This can be obtained by simplifying the square of m(t).We have:m(t)2 = [(1/6) et + (2/6) e2t + (3/6) e3t]2= [(1/6)2 et2 + 2(1/6)(2/6) et e2t + 2(1/6)(3/6) et e3t + (2/6)2 e4t + 2(2/6)(3/6) e2t e3t + (3/6)2 e6t]Now,E(Y2) = (1/6)2 E(et2) + 2(1/6)(2/6) E(et e2t) + 2(1/6)(3/6) E(et e3t) + (2/6)2 E(e4t) + 2(2/6)(3/6) E(e2t e3t) + (3/6)2 E(e6t)Once again, we use the formula for the expected value of et, e2t, e3t, e4t, e5t, and e6t to obtain the following: E(et2) = ∫et2 × et dx from 0 to ∞ = [et3/3] from 0 to ∞ = ∞, so E(et2) = ∞E(et e2t) = ∫et e2t × et dx from 0 to ∞ = [(1/2) e3t] from 0 to ∞ = ∞, so E(et e2t) = ∞E(et e3t) = ∫et e3t × et dx from 0 to ∞ = [(1/2) e4t] from 0 to ∞ = ∞, so E(et e3t) = ∞E(e4t) = ∫e4t × et dx from 0 to ∞ = [(1/4) e4t] from 0 to ∞ = ∞, so E(e4t) = ∞E(e2t e3t) = ∫e2t e3t × et dx from 0 to ∞ = [(1/3) e5t] from 0 to ∞ = ∞, so E(e2t e3t) = ∞E(e6t) = ∫e6t × et dx from 0 to ∞ = [(1/6) e6t] from 0 to ∞ = ∞, so E(e6t) = ∞Therefore,E(Y2) = ∞As we already obtained E(Y) to be infinity, the variance of the given random variable V(Y) = ∞ - ∞2= ∞Thus, V(Y) is infinity.
The distribution of Y To find the distribution of Y, we need to simplify m(t).We have:m(t) = (1/6) et + (2/6) e2t + (3/6) e3tWe can write the equation as:m(t) = (1/6) e0t + (2/6) e2t + (3/6) e3tAs we can see, m(t) can be expressed in the form of the weighted sum of three exponential distributions with different parameter values. This means that the distribution of Y is a mixture of three exponential distributions with parameters 1, 2, and 3.
Learn more about exponential distributions
brainly.com/question/31130457
#SPJ11
Two cars leave the park at the same time opposite directions one goes 3 times faster after 6 hours they travel 140miles how fast did theyg go
Answers
Answer:
Their speeds are;
5.83 mph and 17.49 mph
Step-by-step explanation:
We are told that they leave the park the same time.
Let the speed one car traveled be v
Since the other car is 3 times faster, then it means that, it's speed is 3v.
Now, after 6 hours they travel 140 miles.
We know that;
Speed = distance/time.
Thus;
(v + 3v) = 140/6
4v = 140/6
v = 140/24
v = 5.83 mph
Thus, second car's speed = 3v = 3 × 5.83 = 17.49 mph
Please answer this in two minutes

Answers
hope its helpful to uh...

Type the correct answer in each box. Use numerals instead of words.
Harry buys a boat in 2010. He plans on selling it in 2020. In 2010, the boat costs $20,000. The value of the boat depreciates over time
as is shown in the graph below, where the y-axis represents the value of the boat, in dollars, and the x-axis represents the number of
years since 2010.

Answers
Answer:
The initial value of the boat was $20,000
The percent decrease per year of the value of the boat is 10%.
The interval on which the value of the boat is decreasing while Harry has it is (0,10)
Step-by-step explanation:
It is given that the boat costs $20,000 in 2010 when x = 0. So, the initial value of the boat was $20,000.
Next, find the percent decrease per year of the value of the boat. Consider the general form of an exponential equation, y = a(b)x, where a is the initial value of the boat, b is the base of the exponent, x is the number of years after 2010, and y is the value of the boat, in dollars.
Consider the point (1 , 18,000) which lies on the graph of this situation. Substitute x = 1, y = 18,000, and a = 20,000 into the exponential equation and isolate b.
Recall that for exponential decay, b = 1 - r where r represents the decay rate. Substitute b = 0.9 into this equation and solve for r.
So, the decay rate is 0.1, and the percent decrease per year of the value of the boat is 10%.
Harry bought the boat in 2010, and plans on selling it after 10 years in 2020. Therefore, the interval on which the value of the boat is decreasing while Harry has it is [0, 10].
Pls help if u can ! For brainly

Answers
Answer:
5/8
Step-by-step explanation:
1/4+3/8=5/8
there are 8 pairs of black socks and 4 pairs of white socks in a drawer. how likely is it that you would randomly pick a black pair of socks
Answers
Answer: I would pick black socks too because there are 8 pair of black socks with 4 pairs of white socks and 8 is > greater than 4.
Okay, so...
If there are 8 black socks + 4 white socks, then it = 12 socks totall. the fract Would Be 8/12 but if you simplify it, its 4/6, if you simplify it one more time you final answer is.....
You will have a 2/3 chance of picking a black sock.
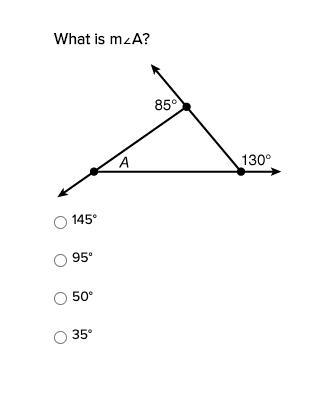
What is m∠A?
145°
95°
50°
35°
Answers
Answer:
35°
Step-by-step explanation:
Since all straight lines have a degree of 180, we can find the measures of the other two angles.
180-85= 95
180-130=50
The sum of the measures of the degrees in a triangle is 180. So if we add m∠A + 95+50 it should equal 180.
We can solve that equation to get the measure of ∠A.
m∠A +145=180
m∠A=35°
Find The Total Differentials Of The Following Utility Functions. A. U(X,Y)=Xαyβ B. U(X,Y)=X2+Y3+Xy
Answers
A. The total differential of the utility function U(X,Y) = X^αY^β is dU = αX^(α-1)Y^β dX + βX^αY^(β-1) dY.
B. The total differential of the utility function U(X, Y) = X^2 + Y^3 + XY is dU = (2X + Y) dX + (3Y^2 + X) dY.
A. The total differential of a function represents the small change in the function caused by infinitesimally small changes in its variables. In this case, we are given the utility function U(X, Y) = X^αY^β, where α and β are constants.
To find the total differential, we differentiate the utility function partially with respect to X and Y, and multiply the derivatives by the differentials dX and dY, respectively.
For the partial derivative with respect to X, we treat Y as a constant and differentiate X^α with respect to X, which gives αX^(α-1). We then multiply it by the differential dX.
Similarly, for the partial derivative with respect to Y, we treat X as a constant and differentiate Y^β with respect to Y, resulting in βY^(β-1). We then multiply it by the differential dY.
Adding these two terms together, we obtain the total differential of the utility function:
dU = αX^(α-1)Y^β dX + βX^αY^(β-1) dY.
This expression represents how a small change in X (dX) and a small change in Y (dY) affect the utility U(X, Y).
B. To find the total differential of the utility function U(X, Y) = X^2 + Y^3 + XY, we differentiate each term of the function with respect to X and Y, and multiply the derivatives by the differentials dX and dY, respectively.
For the first term, X^2, we differentiate it with respect to X, resulting in 2X, which is then multiplied by dX. For the second term, Y^3, we differentiate it with respect to Y, resulting in 3Y^2, which is multiplied by dY. Finally, for the third term, XY, we differentiate it with respect to X and Y separately, resulting in X (multiplied by dY) and Y (multiplied by dX).
Adding these three terms together, we obtain the total differential of the utility function:
dU = (2X + Y) dX + (3Y^2 + X) dY.
This expression represents how a small change in X (dX) and a small change in Y (dY) affect the utility U(X, Y).
Learn more about derivatives here: brainly.com/question/29144258
#SPJ11
Standard Form & Scientific Notation• 3 examples of converting from standard form to scientific notation• 3 examples of converting from scientific notation to standard form
Answers
Required:
We need to convert from standard form to scientific notation and also scientific notation to standard form.
Explanation:
a) Convert from standard form to scientific notation:
1) Consider the number 4,520,000.
The given number can be written as follows.
\(4,520,000=452\times10000\)\(=452\times10^4\)\(=452\times10^4\times\frac{10^2}{10^2}\)\(=452\times\frac{10^4\times10^2}{10^2}\)\(=\frac{452}{100}\times10^6\)\(=4.52\times10^6\)The scientific notation of s
\(4.52\times10^6\)2) Consider the number
\(35.98\times10^3\)Multiply and divide by 10.
\(35.98\times10^3=35.98\times10^3\times\frac{10}{10}\)\(=\frac{35.98}{10}\times10^3\times10\)\(=3.598\times10^4\)The scientific notation is
\(3.598\times10^4\)3) Consider the number.
\(600.89\times10^{-8}\)Multiply and divide by 100.
\(600.89\times10^{-8}=600.89\times10^{-8}\times\frac{100}{100}\)\(=\frac{600.89}{100}\times10^{-8}\times10^2\)\(=6.0089\times10^{-6}\)The scientific notation is
\(6.0089\times10^{-6}\)b) convert from scientific notation to standard form:
1)
Consider the notation:
\(6.285\times10^{-5}\)\(Use\text{ }10^{-5}=\frac{1}{100000}.\)\(6.285\times10^{-5}=\frac{6.285}{100000}\)\(=0.00006285\)The standard form is 0.00006285.
2) Consider the notation.
\(7.9\times10^4\)\(Use\text{ }10^4=10000.\)\(7.9\times10^4=7.9\times10000\)\(=79000\)The standard form is 79,000.
3) Consider the notation.
\(9.008\times10^5\)\(Use\text{ }10^5=100000.\)\(9.008\times10^5=9.008\times100000\)\(9.008\times10^5=900800\)The standard form is 900,800.