Answers
Answer:
C, B, D, A
Step-by-step explanation:
A = 40
B = 30
C = 24
D = 36
Related Questions
Everyone thought that Martha Mathy was trying to start a new fashion trend when she started wearing socks that did not match. her "look" started to catch on, and pretty soon all the kids at her school were wearing mixed-up socks, too. Rita Writer, a reporter for the school paper, interviewed Martha about the new sock trend. " Wat gave you the idea to wear mismatched socks?" Rita Asked.
"Its simple mathematics," Martha replied. "you see, I have 18 socks at home but no two are the same. with just these 18 socks, I can create over 100 unique pairs of mismatched socks." Rita found this hard to believe, so she checked it out. Was Martha correct?
Answers
Answer:
There are 153 combinations
Combinations - any two from eighteen is given by the formula 18C2 or 18! / (2!*16!)
= 18 * 17 / 2 = 153
OK that is the maths - now the explanation
The first sock can be any of 18
The second sock can be any of 17 (one already been selected and they must be mismatched)
Therefore there are 18*17 = 306 permutations she could make
However the question asks for "combinations" not "permutations"
A green sock on the right foot and a yellow sock on the left foot is deemed to be a different "permutation" to a yellow sock on the right foot and a green sock on the left foot. HOWEVER, they are regarded as the same "combination" in both cases you have one green and one yellow sock.
Therefore for combinations we must divide the 306 permutations calculated above by 2 = 153
FYI Walton has incorrectly given you the value of 18!. That would only apply if Martha Mathy had 18 feet!
Given sinz = -4/5 for pi < z < (3pi)/2, find the value of cosz.

Answers
The angle z is in the third quadrant, the value of cosz is negative. Hence, cosz = -3/5.So, the value of cosz is -3/5.
Given sinz = -4/5 for pi < z < (3pi)/2, we need to find the value of cosz. We can use the trigonometric identity of Pythagorean theorem to find the value of cosz.
According to Pythagorean theorem, sin2θ + cos2θ = 1, where θ is the angle in the right-angled triangle and sin, cos are the trigonometric ratios.
The negative sign for the given sinz indicates that the angle z is in the third quadrant. So, we can take the help of the unit circle to find the value of cosz as shown below:
Here, we have used the Pythagorean identity of sin2z + cos2z = 1 on the unit circle to find the value of cosz. Since the value of sinz is already given, we can find the value of sin2z as: sin2z = sinz x sinz = (-4/5) x (-4/5) = 16/25
Then, we can substitute the value of sin2z in the Pythagorean identity as: cos2z = 1 - sin2z = 1 - (16/25) = 9/25We need to find the value of cosz.
So, we can take the square root of cos2z as: cosz = ±(√(9/25)) = ±(3/5)The sign of cosz can be determined by considering the quadrant of the angle z.
Since the angle z is in the third quadrant, the value of cosz is negative. Hence, cosz = -3/5.So, the value of cosz is -3/5.
For more questions on angle.
https://brainly.com/question/31615777
#SPJ8
How many students are enrolled in hip hop or ballroom?
Answers
In order to find how many students are enrolled in either class, hip hop or ballroom, we look at the possibilities; in this case, the only possibility in which the student is not enrolled in either is if the student is only enrolled in Latin, for that reason the number of students enrolled in hip hop or ballroom is:
\(13+28+9+17+25+29=121\)hens usually begin laying eggs when they are about 6 months old. young hens tend to lay smaller eggs than older hens. assume that the average weight of the eggs produced by the young hens is 50 grams, and the standard deviation of the weight of the eggs is 4 grams. assume further that the weight of the eggs from young hens (x) follows a normal distribution. a. (3 pts) what is the probability that a randomly selected egg laid by a young hen weighs less than the desired minimum weight of 55 grams, imposed by the department of agriculture? show your work.
Answers
The probability that a randomly selected egg laid by a young hen weighs less than 55 grams is approximately 0.1056, or 10.56%.
To find the probability that a randomly selected egg laid by a young hen weighs less than the desired minimum weight of 55 grams, we need to calculate the z-score and use the standard normal distribution table.
Step 1: Calculate the z-score.
z = (x - μ) / σ
where x is the desired weight (55 grams), μ is the average weight (50 grams), and σ is the standard deviation (4 grams).
z = (55 - 50) / 4
z = 5 / 4
z = 1.25
Step 2: Use the standard normal distribution table to find the probability.
Look up the value 1.25 in the table and find the corresponding probability. The value for z = 1.25 is approximately 0.8944.
Step 3: Subtract the probability from 1.
Since the table gives the probability of the weight being less than 55 grams, we need to subtract the value from 1.
1 - 0.8944 = 0.1056
for such more question on probability
https://brainly.com/question/24756209
#SPJ11
3 1/3 - 5 1/2 in fraction form
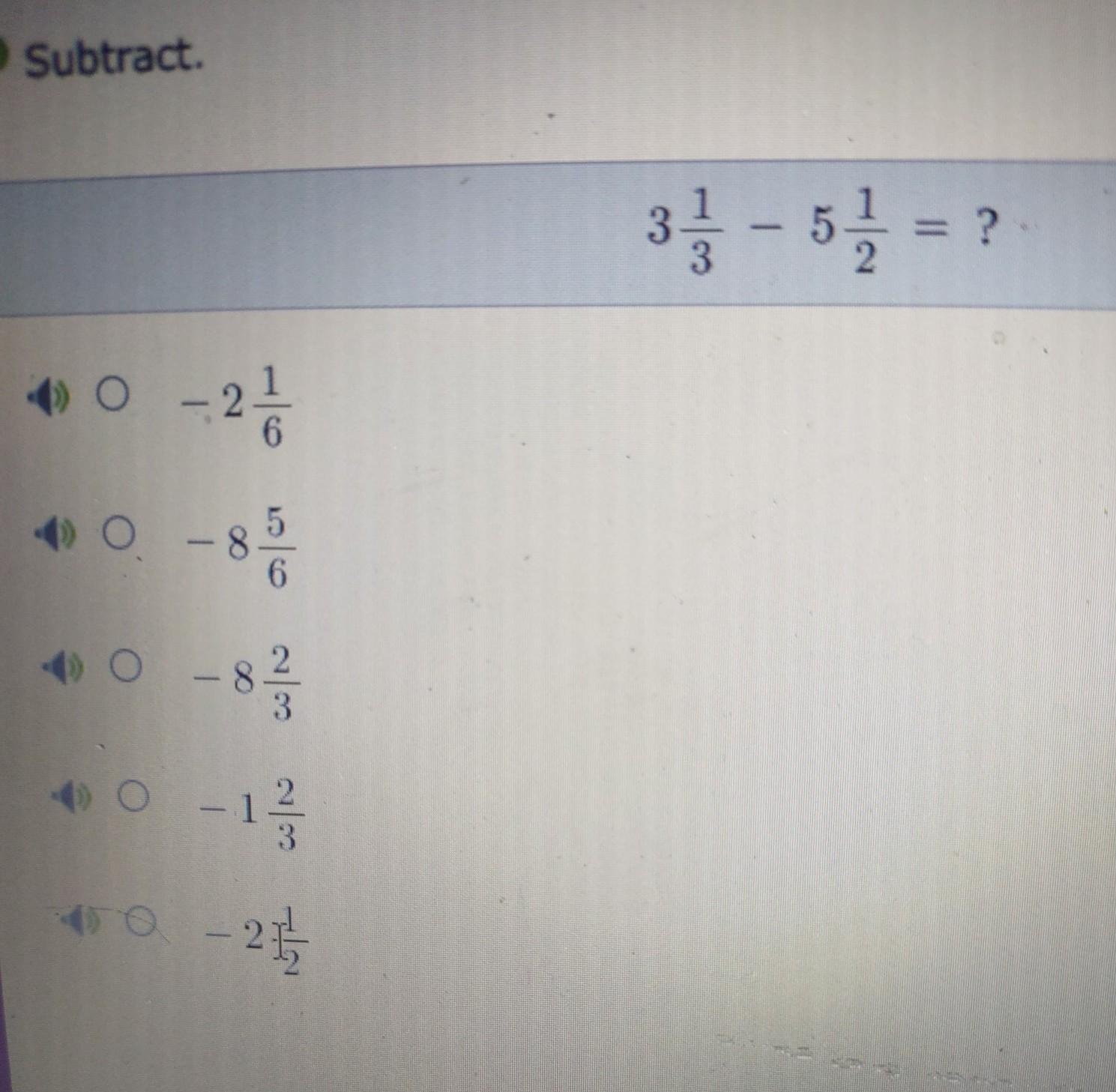
Answers
Explanation:
3 1/3 = 10/3
5 1/2 = 11/2
10/3 - 11/2
10/3 = 20/6
11/2 = 33/6
20/6 - 33/6 = -13/6
-13/6 = -2 1/6
Hope this helps!

Find the principal needed now to get the given amount; that is, find the present value.
To get $600 after 4 years at 7% compounded monthly
Answers
The required present value needed now to get $700 after 4 years at 11% compounded monthly is $451.73.
To find the present value of $600 after 4 years at 7% compounded monthly, we can use the formula for compound interest:
Compound Interest =P(1+r/n)^rt
Substituting the given values, we get:
Compound Interest =600 (1+7/n)^4
Simplifying this equation, we get
P = 600 / 1.487
P = 451.73
Therefore, the present value needed now to get $600 after 4 years at 7% compounded monthly is $451.73.
Learn more about present value here:
brainly.com/question/17322936s
#SPJ1
Help me if you can please

Answers
Answer:
the question is not visible
Megan has 7 packs of pens. She gives 5 pens to her friend. Megan has 30 pens left over.
How many pens are in each pack?
A: 5 pens
B: 6 pens
C: 10 pens
D: 12 pens
Answers
Answer:
A: 5 pens----------------------
Let each pack have x pens, then 7 packs have 7x pens.
Megan gives 5 pens to her friend and 30 pens left over. Set up an equation and solve for x:
7x - 5 = 307x = 35x = 5There are 5 pens in each pack.
Answer:
Answer A is correct
Step-by-step explanation:
Megan starts with 7 packs of pens.
Let the number of pens in each pack be x
So initially, Megan has a total of 7x pens.
Then she gives 5 pens to her friend.
After giving away 5 pens, she has 7x - 5 pens left.
According to the problem, Megan has 30 pens left over.
Therefore, we can set up the equation like this:
7x - 5 = 30
Solve for x.
7x = 30 + 5
7x = 35
Dividing both sides by 7.
x = 35/7
x = 5
Therefore, there are 5 pens in each pack.
So, Megan has 7 packs of pens, and each pack contains 5 pens.
2) In a random survey of 500 women, 315 said they would rather be poor and thin than rich and fat; in a random survey of 400 men, 220 said they would rather be poor and thin than rich and fat. Is there sufficient evidence to show that the proportion of women who would rather be poor and thin than rich and fat is greater than the proportion of men who would rather be poor and thin than rich and fat
Answers
Answer:
Since the calculated value of Z= 0.242887 is less than Z (0.05) = 1.645 and falls in the critical region we reject the null hypothesis and conclude that there is not sufficient evidence to show that the proportion of women who would rather be poor and thin than rich and fat is greater than the proportion of men who would rather be poor and thin than rich and fat.
Step-by-step explanation:
Here
p1= proportion of women who would rather be poor and thin than rich and fat
p1= 315/500= 0.63
p2= proportion of men who would rather be poor and thin than rich and fat
p2= 220/400= 0.55
1) Formulate the hypothesis as
H0: p1>p2 against the claim Ha: p1 ≤ p2
2) Choose the significance level ∝0.05
3) The test Statistic under H0 , is
Z= p1^ - p2^ / sqrt( pc^qc^( 1/n1 + 1/n2))
pc^= an estimate of the common proportion
pc ^ = n1p1^ + n2p2^/ n1+n2
4) The critical region is Z≤ Z (0.05) = 1.645
5) Calculations
pc^ = 315+ 220/ 500+400= 535/900
pc^= 0.5944
and qc^= 1-0.5944= 0.4055
Thus
Z = 0.63-0.55/ sqrt ( 0.5944*0.4055( 1/500+ 1/400))
Z= 0.08/ sqrt (0.24108 (900/2000))
Z= 0.08/√0.10849
Z= 0.242887
Conclusion :
Since the calculated value of Z= 0.242887 is less than Z (0.05) = 1.645 and falls in the critical region we reject the null hypothesis and conclude that there is not sufficient evidence to show that the proportion of women who would rather be poor and thin than rich and fat is greater than the proportion of men who would rather be poor and thin than rich and fat.
what is the measure of angle b

Answers
Answer:
34
Step-by-step explanation:
A triangle will add up to a degree of 180, so if you add those 2 angles then subtract it from 180 you will get the answer. So, 115+31=146 then 180-146=34
So the answer is 34
Answer:
b = 34 degrees
Step-by-step explanation:
*triangles have an interior angle of 180 degrees
to find b, take the known angles (115 and 31) add them together and subtract the sum from 180:
⇒ 180 - (115 + 31)
solve:
⇒ 180 - 146 = 34
b = 34
Question 10
A car park has 880 parking spaces.
Some of the spaces are reserved.
The ratio of reserved spaces: not reserved spaces = 1:10.
Work out the number of spaces that are not reserved.
Answers
Step-by-step explanation:
work he in a department store
El mcd de 36 90 y 18
Answers
Answer:
whut
Step-by-step explanation:
Juan Hernandez, a Cuban athlete who visits the United States and Europe frequently, is allowed to return with a limited number of consumer items not generally available in Cuba. The items, which are carried in a duffel bag, cannot exceed a weight of 5 pounds. Once Juan is in Cuba, he sells the items at highly inflated prices. The three most popular items in Cuba are denim jeans, CD players, and CDs of U.S. rock groups. The weight and profit (in U.S. dollars) of each item are as follows:
Item Weight (lb.) Profit
Denim jeans 2.1 $40
CD players 3.2 48
Compact discs 0.8 16
uan wants to determine the combination of items he should pack in his duffel bag to maximize his profit. This problem is an example of a type of integer programming problem known as a "knapsack" problem. Formulate and solve the problem.
Answers
Answer:
z (max) = 96
x₁ = 2
x₂ = 0
x₃ = 1
Step-by-step explanation:
Fromproblem statement:
weight (lb) . Profit $
Denim jeans 2.1 40
CD players 3.2 48
Compact Discs 0.8 16
Objective Function z is:
z = 40*x₁ + 48*x₂ + 16*x₃ to maximize
Subject to:
Weight constrain: 5 lb
2.1*x₁ + 3.2*x₂ + 0.8*x₃
x₁≥ 0 x₂ ≥ 0 x₃ ≥ 0 All integers
Using AtomZmath on-line solver and after 2 iterations
Solution:
z (max) = 96
x₁ = 2
x₂ = 0
x₃ = 1
The maximized profit is the highest profit Juan can get by selling his items.
The maximized profit is $96
Let x represents the Denim jeans, y represents the CD players and z represent the compact discs.
So, we have the following parameters
Weights
\(x = 2.1\)
\(y = 3.2\)
\(z = 0.8\)
The weight cannot exceed 5 pounds.
So, the constraint is
\(2.1x + 3.2y + 0.8z \le 5\)
The profit is given as:
\(x = 40\)
\(y = 48\)
\(z = 16\)
So, the objective function to maximize is
\(Max\ Z = 40x + 48y + 16z\)
The integer programming model is then represented as:
\(Max\ Z = 40x + 48y + 16z\)
Subject to:
\(2.1x + 3.2y + 0.8z \le 5\)
\(x,y,z \ge 0\)
Using a graphing calculator, the values that maximize the objective function are:
\(x = 2\)
\(y = 0\)
\(z = 1\)
Substitute these values in the objective function
\(Max\ Z = 40x + 48y + 16z\)
\(Z = 40 \times 2 + 48 \times 0 + 16 \times 1\)
\(Z = 80 + 0 + 16\)
\(Z = 96\)
Hence, the maximized profit is $96
Read more about integer programming at:
https://brainly.com/question/13841397
The ratio of girls to boys on the school bus was 4:3 , if there were 28 girls, how many boys were there
Answers
Answer:
the answer is 21 because
Step-by-step explanation:
28÷4=7
28-7=21
Answer:
21 boys
Step-by-step explanation:
girls:boys
4:3
28:x
girls:
4 became 28 by multiplying 4 by 7
So do the same to boys
Therefore,
when we multiply 3 by 7
=21 boys
Hope you got it
If you have any question just ask me
If you think this is the best answer please mark me as BRAINLIEST
5 + k – 5k = -4k + 6 0
Answers
Answer:
Step-by-step explanation:
Step 1: Simplify both sides of the equation.
5+k−5k=−4k+60
5+k+−5k=−4k+60
(k+−5k)+(5)=−4k+60(Combine Like Terms)
−4k+5=−4k+60
−4k+5=−4k+60
Step 2: Add 4k to both sides.
−4k+5+4k=−4k+60+4k
4+4+4+5+5+5+5+5+5+5+5+5+5+5=
Answers
Answer:
67 ans
Step-by-step explanation:
please mark me as brainlist
Answer:
67
Step-by-step explanation:
What is 96 divided by 9697?
Answers
Answer:0.0098
Step-by-step explanation:
If AD = 21, BF = 8, and DF = 8, what is the value of AB?

Answers
Answer:
AB would be 21
Step-by-step explanation:
Sides BF and DF equal 8, because triangles BFC and DFC are both right triangles and they have two equal sides (hypotenuses are equal and both triangles share side FC), triangles BFC and DFC are congruent triangles, which means side DC is equal to BC. Since right triangles ADC and ABC share side AC and BC = DC, they are congruent triangles, meaning AB will equal AD, which is 21.
f(x)=x^2. What is g(x)?

Answers
Answer:
D, g(x) = 1/4 x^2
Step-by-step explanation:
You can try plugging in the x and y values into each equation. The answer to this would be D, where if you plug in 2 as the x value, you get 1/4 * 4 which equals 1. This also makes sense because 2x would have a narrower curve while 1/2x would have a wider curve.
A car-carrier trailer weighs 35,000 pounds when empty. The driver loads 7 cars on the trailer. The cars are identical except for color. The weight of the loaded trailer is 50,855 pounds. The maximum vehicle weight allowed on U.S. highways is 80,000 pounds. What number best describes the weight of one car?
Answers
Answer:
Each car weighs 2,265 pounds
Step-by-step explanation:
Given that the car carrier weighs 35,000 pounds when empty, that is, without cars, and that loading 7 cars its weight is 50,855 pounds, the difference between both values implies the weight of the 7 cars together, which is determined through the following calculation:
50,855 - 35,000 = X
15.855 = X
Thus, the weight of the 7 cars together is 15,855 pounds. In turn, the weight of each particular car is determined from the following division:
15.855 / 7 = X
2,265 = X
Therefore, each car weighs about 2,265 pounds.
Simplify:
14f – 5s + 6f – 20 + 17s – 2f
Answers
\(\huge\text{Hey there!}\)
\(\large\text{14f - 5s + 6f - 20 + 17s - 2f}\)
\(\large\textsf{COMBINE the LIKE TERMS}\)
\(\large\text{(14f + 6f - 2f) + (-5s + 17s) + (-20)}\)
\(\large\textsf{SOLVING for the F-VALUES}\)
\(\large\text{14f + 6f - 2f}\\\large\text{14f + 6f = \bf 20f}\\\large\text{20f - 2f = \bf 18f}\)
\(\large\textsf{SOLVING for the S-VALUES}\)
\(\large\text{-5s + 17s = \bf 12s}\)
\(\large\text{-20 \textsf{will stay the same because there is NOT any like terms for it}}\)
\(\large\text{-20 = \bf -20}\)
\(\boxed{\boxed{\large\textsf{Answer: \huge \bf {18f + 12s - 20}}}}\huge\checkmark\)
\(\large\textsf{Good luck on your assignment and enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
The graph shows the function f(x).
On a coordinate plane, a cube root function goes through (8, 2), has an inflection point at (0, negative 1), and goes through (8, negative 3).
Which equation represents f(x)?
f(x) = Negative RootIndex 3 StartRoot x EndRoot
f(x) = Negative RootIndex 3 StartRoot x minus 1 EndRoot
f(x) = Negative RootIndex 3 StartRoot negative x EndRoot minus 1
f(x) = Negative RootIndex 3 StartRoot negative x EndRoot
Answers
The equation that represents the given data is \(\RM \\f(x) = -\sqrt[3]{-x} ,\) Option D is the correct answer.
What is a Function ?It is a statement where two variables , one dependent and one independent are related.
It is given that
a cube root function goes through (8, 2), has an inflection point at (0, negative 1), and goes through (8, negative 3).
The equation given in the options are
\(\rm f(x) = -\sqrt[3]{x} \\f(x) = -\sqrt[3]{x-1} \\f(x ) =-\sqrt[3]{-x} -1 \\f(x) = -\sqrt[3]{-x}\)
The function goes through (8,2)
Substituting the values
f(x) = -2
f(x) = \(\sqrt[3]{7}\)
f(x) = -3
f(x) = 2
The equation that represents the given data is
\(\RM \\f(x) = -\sqrt[3]{-x} ,\) Option D is the correct answer.
To know more about Function
https://brainly.com/question/12431044
#SPJ1
Answer:
D
Step-by-step explanation:
4. What is Probability?
(ii) State the axioms of probability
(iii)Two fair dice are thrown, what is the probability of getting
(a) the sum of 9
(b) two odd numbers
(c) two prime numbers
(d) two factors of 12
4c. What is Statistics?
Answers
(i) Probability is a notion in Mathematics which describes the likelihood of an event or a set of events occurring. It is a measure of uncertainty when estimating the outcome of an experiment or an observation.
(ii) The axioms of probability are:
the non-negativity (that the probability of an event is greater than or equal to zero), and
the additivity (that the probability of the union of two or more mutually exclusive events is equal to the sum of their individual probabilities).
(iii) When two fair dice are thrown the probability of getting:
a) The sum of 9 = 1/9
b) Two odd numbers = 1/4
c) two prime numbers = 1/9
d) two factors of 12 = 1/9
(iv) Statistics is a branch of mathematics that deals with data collection, analysis, interpretation, presentation, etc.
How to find probability when two dice are thrown?To find probability when two dice are thrown, we have:
(a) The sum of 9:
We will estimate the number of ways to get a sum of 9: (3,6), (4,5), (5,4), and (6,3) = 4 ways
A die has 6 possible outcomes, the total number of possible outcomes is 6x6=36 = 4/36 = 1/9.
(b) Two odd numbers:
We count the number of ways to get two odd numbers: (1,3), (1,5), (1,7), (3,1), (3,5), (3,7), (5,1), (5,3), and (5,7).
possible outcomes = 9,
So, the total possible outcomes = 6x6=36 = 9/36 = 1/4.
(c) Two prime numbers
We estimate the number of ways we can get two prime numbers: (2,3), (3,2), (5,2), and (2,5)
possible outcomes = 4,
So, the total possible outcomes = 6x6 =36 = 4/36, = 1/9.
(d) Two factors of 12:
We count the number of ways and divide by the total possible outcomes.
The factors of 12 are 1, 2, 3, 4, 6, and 12: (2,6), (3,4), and (4,3) = 3 ways
possible outcomes = 6
Therefore, the total number of possible outcomes = 6x6=36 = 3/36, = 1/12
Learn more about probability at brainly.com/question/13604758
#SPJ1
At the start of the year, 90 people were going to the gym. If 55.6% of them quit going a month later, how many people are going to the gym now?
Answers
Answer: 39.96 people
Step-by-step explanation:
If 55.6% quit, that means 44.4% still go to the gym.
44.4%*90 = 39.96 people
f(s) = 3s + 2
p(s) = s³ + 4s
Find (f • p)(-5)
Answers
Step-by-step explanation:
To evaluate (f • p)(-5), we first need to find the composite function f(p(-5)):
p(-5) = (-5)³ + 4(-5) = -125 - 20 = -145
f(p(-5)) = 3(-145) + 2 = -435 + 2 = -433
Therefore, (f • p)(-5) = f(p(-5)) = -433.
Your neighbor is digging a hole in his back yard for an in-ground swimming pool. The rectangular hole is 8 feet wide, 16 feet long, and 7 feet deep. If his pickup truck can haul one cubic meter, how many trips will it take him to haul all of the dirt away?
(please show work)
Answers
There are 896 trips will it take him to haul all of the dirt away.
What is Multiplication?To multiply means to add a number to itself a particular number of times. Multiplication can be viewed as a process of repeated addition.
Given that;
The rectangular hole is 8 feet wide, 16 feet long, and 7 feet deep.
Now,
Since, The rectangular hole is 8 feet wide, 16 feet long, and 7 feet deep.
And, His pickup truck can haul one cubic meter.
Hence, Number of trips will it take him to haul all of the dirt away will be;
⇒ 16 × 7 × 8 / 1
⇒ 896
Thus, Number of trips = 896
Learn more about the multiplication visit:
https://brainly.com/question/28768606
#SPJ1
10. Prime numbers from 1 to 100 are running a restaurant - PRIME SPOT, near a tourist point. On a winter holiday, 1 and the composite numbers up to 100 enter the restaurant for dinner after their picnic at the same point. The dining hall has tables with seating capacity 15 for each. If they occupy tables without leaving any chair free, how many tables are required? If each prime number attender has to serve equal number of customers, how many customers should each one get to serve?
Answers
6 tables are required. Each prime number attender should serve 3 customers each.
The prime numbers between 1 and 100 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
All the numbers other than prime numbers are composite numbers.
The composite numbers from 1 to 100 are: 1, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.
Now, as there are 25 primes and 75 composites in the group that visited the restaurant, we can calculate the number of tables required by dividing the number of people by the seating capacity of each table.
Each table has a seating capacity of 15, so the number of tables required will be: Number of tables = (Number of customers)/(Seating capacity of each table)Number of customers = 25 (the number of primes) + 75 (the number of composites) = 100Number of tables = 100/15 = 6 tables
Therefore, 6 tables are required.
Now, as each prime number attender has to serve an equal number of customers, we need to calculate how many customers each one should serve.
Each prime attender has to serve 75/25 = 3 customers each, as there are 75 composites and 25 primes.
Thus, each prime number attender should serve 3 customers each.
For more questions on prime number
https://brainly.com/question/145452
#SPJ8
Penelope goes out to lunch. The bill, before tax and tip, was $16.05. A sales tax of 3% was added on. Penelope tipped 18% on the amount after the sales tax was added. How much tip did she leave? Round to the nearest cent.
Answers
Answer:
2.98
Step-by-step explanation:
First find 3% of 16.05 which is 0.48.
Then add 0.48 to 16.05 which is 16.53.
Then multiply .18 by 16.53 which gets you 2.98
Hope it helps
Answer:
To find the amount of the sales tax, we need to multiply the bill amount by the tax rate of 3% or 0.03:
Sales tax = 0.03 x $16.05 = $0.48
To find the total amount of the bill after the sales tax was added, we need to add the bill amount to the sales tax:
Total bill = $16.05 + $0.48 = $16.53
To find the amount of the tip, we need to calculate 18% of the total bill after the sales tax was added:
Tip = 0.18 x $16.53 = $2.98
Rounding to the nearest cent, Penelope left a tip of $2.98.
Step-by-step explanation:
The graph of linear function fpasses through the point (1, -9) and has a slope of 3.
What is the zero of f?
4
-2
2
-6
Will give brainliest if your right

Answers
Slope=-3
Coordinates= (1,-9)
uno de los catetos del triangulo rectángulo mide 77cm y la hipotenusa excede al otro cateto en 49 cm.
CALCULA LA HIPOTENUSA
Answers
La hipotenusa mide 137 cm.
Podemos utilizar el teorema de Pitágoras para resolver este problema, que establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Sea "a" la medida del otro cateto, entonces:
a² + 77² = (a+49)²
Desarrollando los cuadrados y simplificando, tenemos:
a² + 5929 = a²+ 98a + 2401
Restando a ambos lados a², obtenemos:
5929 = 98a + 2401
Restando 2401 a ambos lados, obtenemos:
3528 = 98a
Dividiendo por 98, obtenemos:
a = 36
Por lo tanto, el otro cateto mide 36 cm, y la hipotenusa se puede calcular utilizando el teorema de Pitágoras:
h² = a² + b²
h2 = 36² + 77²
h² = 12996 + 5929
h² = 18925
Tomando la raíz cuadrada en ambos lados, obtenemos:
h = 137
Por lo tanto, la hipotenusa mide 137 cm.
Aprende más sobre el rectángulo,
https://brainly.com/question/25292087
#SPJ1
