patricia will flip the coin 8 times. let a be the event that exactly 4 of the 8 flips are heads, and b be the event that the last two flips are tails. find p(a ∪ b).
Answers
The probability of an event of P(A∪B) is 49/128.
In this question,
Patricia will flip the coin 8 times.
The sample space is the flipping of a coin 8 times.
⇒ n(s) = 2⁸
⇒ n(s) = 256
Let A be the event that exactly 4 of the 8 flips are heads
⇒ n(A) = \(8C_4\) [∵ \(nC_r=\frac{n!}{r!(n-r!)}\)]
⇒ \(\frac{8!}{4!4!}\) = 70
Then, P(a) = \(\frac{n(a)}{n(s)}\)
⇒ \(\frac{70}{256}\)
Let B be the event that the last two flips are tails
⇒ n(B) = \(8C_2\)
⇒ \(\frac{8!}{2!6!}\) = 28
Then, P(a) = \(\frac{n(b)}{n(s)}\)
⇒ \(\frac{28}{256}\)
Now, P(A∪B) = P(A) + P(B)
⇒ P(A∪B) = \(\frac{70}{256} + \frac{28}{256}\)
⇒ P(A∪B) = \(\frac{70+28}{256}\)
⇒ P(A∪B) = \(\frac{98}{256}\)
⇒ P(A∪B) = \(\frac{49}{128}\)
Hence we can conclude that the probability of an event of P(A∪B) is 49/128.
Learn more about probability of event here
https://brainly.com/question/23182625
#SPJ4
Related Questions
Solve for z.
–8z + 17 = –13 + 2z
z =
Answers
Answer:
\( \boxed{z = 3} \)
Step-by-step explanation:
\( = > - 8z + 17 = - 13 + 2z \\ \\ = > - 8z - 2z + 17 = - 13 \\ \\ = > - 10z + 17 = - 13 \\ \\ = > - 10z = - 13 - 17 \\ \\ = > \cancel{-} 10z = \cancel{-} 30 \\ \\ = > 10z = 30 \\ \\ = > z = \frac{30}{10} \\ \\ = > z = 3\)
Answer:
z = 3
Step-by-step explanation:
→Add 8z to both sides:
-8z + 17 = -13 + 2z
17 = -13 + 10z
→Add 13 to both sides:
30 = 10z
→Divide both sides by 10:
3 = z
What is the slope of the line represented by the equation y = - 2/3 - 5x?
-5
-2/3
2/3
5
Answers
Answer:
The slope is the bit attached to the x:
In this case, it is -5.
Step-by-step explanation:
Answer: -5
just took the quiz
#4) Choose the graph that matches the equation below.
y = -x
A
C
2/3
B
D
QUICK CHECK !!

Answers
Answer:
the correct is D the graph is a decreasing function
A simple random sample of 60 items resulted in a sample mean of 25. The population standard deviation is o = 7. (Round your answers to two decimal places.) (a) What is the standard error of the mean, 0-? (b) At 95% confidence, what is the margin of error?
Answers
a) The standard error of the mean is 0.90
b) The marginal error is 1.76
Given,
Number of samples in the population, n = 60
Sample mean of the population, μ = 25
Standard deviation of the population, σ = 7
We have to find the standard error of the mean and the margin of error at 95% confidence.
Here,
a) The standard error of the mean = Standard deviation / root of sample
= σ / √n
= 7/√60
= 0.90
b) The margin error;
Zₐ/₂ × σ / √n
= Zₐ/₂ × 7/√60
= 1.96 × 0.90
= 1.76
Therefore,
a) The standard error of the mean is 0.90
b) The marginal error is 1.76
Learn more about standard error and marginal error here;
https://brainly.com/question/17014419
#SPJ1
i need help with solving this!

Answers
Answer:
y=3x-4 (EQ.1)
y=-4x+10 ( EQ.2)
Step-by-step explanation:
On comparing equation 1 and 2
3x-4= -4x+10
3x+4x= 10+4
7x=14
x= 14/7
x=2
Put x in eq 1
y=3x-4
=3(2)-4
= 6-4
=2
Hence, x=2 and y= 2
What evidence is needed to prove two triangles are similar by the SSS similarity theorem?
Answers
Consider the same figure as given above. It is observed that DP/PE = DQ/QF and also in the triangle DEF, the line PQ is parallel to the line EF.
So, ∠P = ∠E and ∠Q = ∠F.
Hence, we can write: DP/DE = DQ/DF= PQ/EF.
The above expression is written as
DP/DE = DQ/DF=BC/EF.
It means that PQ = BC.
Hence, the triangle ABC is congruent to the triangle DPQ.
(i.e) ∆ ABC ≅ ∆ DPQ.
Thus, by using the AAA criterion for similarity of the triangle, we can say that
∠A = ∠D, ∠B = ∠E and ∠C = ∠F.
To know more about triangle check the below link:
https://brainly.com/question/1058720
#SPJ4
solve the following equation for y: 35x - 7y = 49, what is the slope?
Answers
Answer:
y = 5x - 7
slope = 5
Step-by-step explanation:
35x - 7y = 49
Subtract 35x from both sides.
-7y = -35x + 49
Divide both sides by -7.
y = 5x - 7
The equation is now in the slope-intercept form, y = mx + b, where m is the slope.
slope = m = 5
a rectangle with sides of length n+2 and n is compared to a square with sides of length n+1, are the two shape equal in perimeter?
Answers
Answer:
YES
Step-by-step explanation:
Rectangle: (n)+(n)+(n+2)+(n+2)=4n+4
Square: (n+1)+(n+1)+(n+1)+(n+1)=4n+4
4n+4=4n+4
Yes, they are equal in perimeter.
Answer:
they have equal perimeter.
Step-by-step explanation:
perimeter :-
.Rectangle=2(n+2+n)=2(2n+2)=4(n+1)
Square=4(n+1)
2. using calculations based on a perpetual inventory system, determine the inventory balance altira would report in its august 31, 2021, balance sheet and the cost of goods sold it would report in its august 2021 income statement using the average cost method. (round "average cost per unit" to 2 decimal places.)
Answers
As per the given income, the inventory balance on August 31,2021 is $98,002
The term income is referred as the money that a person or entity receives in exchange for their labor or products.
Here we have given that balance sheet and the cost of goods sold it would report in its august 2021 income statement using the average cost method.
And here we also know that on August 2021 Ending Inventory and the Cost of Goods Sold is calculated as,
=> Ending Inventory = 9,000 units at $5.88 per unit
Then the value of ending inventory is written as,
=> 9000 x 5.88 = $52,920
Then the Cost of goods sold is calculated as
=> 9,600 x $5.87 = $56,352
=> 7,000 x $5.95 = $41,650
Therefore, the cost of total goods sold is written as
=> 16,600 units = $98,002
To know more about income here
https://brainly.com/question/7619606
#SPJ4
A person noted that the angle of elevation to the top of a silo was 70° at a distance of 9 feet
from the silo. Using the diagram approximate the height of the silo.
Answers
The height of the silo is 7.36 feet.
According to the question, the given angle of elevation from top is 70 degrees and the distance is 9 feet. And to calculate the height with the given parameters, the trigonometric function which is known as tangent can be used.
Therefore, the standard description about the tangent is the ratio of base and height.
Now, tangent = \(\frac{base}{height}\)
Substitute the values in the above formula:
tan70 = \(\frac{9}{height}\)
Height = 9/tan70=7.36 feet
Hence, the calculated height is 7.36 feet.
What is tangent?
The word tangent can be defined as the ratio of the length of the opposite sides to the adjacent sides. And in another definition, it is the ratio of base and height. In this, the denominator should not be equal to zero otherwise it tends to infinity.
To learn more about the tangent of a line from the given link:
https://brainly.com/question/4470346
#SPJ9
What is 2(x - 9) = 10?
Answers
Answer:
x=14
Step-by-step explanation:
2 times x = 2x and 2 time 9 is 18 so the equation is 2x-18=10. then you add 18 to both sides and get 2x=28 then simplify to x=14
Answer:
x=14
Step-by-step explanation:
2(x-9)=10
Step one - Simplify both sides
(2)(x)+(2)(-9)=10 (distribute)
2x+-18=10
2x-18=10
Step two - Add 18 to both sides
2x-18+18=10+18
2x=28
Step three - Divide both sides by 2
2x÷2 = 28÷2
x= 14
Answer:
x=14
The radius of a circle is 6 inches. What is the area of a sector bounded by a central angle measuring 120°
Answers
Knowing that a circle has a radius of 6 inches, the area of a sector with a central angle of 120º is 12π square inches.
The area of a sector can be found using the formula:
Area of sector = (Central angle/360°) × π × r²
Where "central angle" is the angle of the sector in degrees and "r" is the radius of the circle.
In this case, the central angle is 120° and the radius is 6 inches. Plugging these values into the formula, we get:
Area of sector = (120°/360°) × π × 6²
Area of sector = (1/3) × π × 36
Area of sector = 12π square inches
Therefore, the area of the sector bounded by a central angle measuring 120° in a circle with a radius of 6 inches is 12π square inches.
See more about central angle at https://brainly.com/question/10945528.
#SPJ11
Help anyone can help me do this question,I will mark brainlest.

Answers
Answer:
Step-by-step explanation:
E ⊂ F ⊂ G

Please help me!!!! :(

Answers
Answer:
The point (3/2, -3/2) can be represented as (1.5, -1.5) in decimal form. The x-coordinate, 3/2, is equivalent to 1.5, indicating a movement of 1.5 units to the right from the origin. Similarly, the y-coordinate, -3/2, is equivalent to -1.5, representing a movement of 1.5 units downward from the x-axis.
Visually, the point (1.5, -1.5) is located on the graph slightly to the right and below the origin, as shown below:

how to do this question plz
question 2

Answers
Answer:
a) x+3=19
Step-by-step explanation:
a)
x is the age of Ronald , Collin is three years older than Ronald , so if we add up x(Ronald's age) and 3(the difference between both of their ages), we would get Collin's age(19) . That is the explanation for this equation.
b)
x+3=19
x=19-3
x=16
thus , x is 16 , in other words , Ronald's age is 16.
3x^2 – 8x + 5 = 5x^2
Answers
Answer:
Step-by-step explanation:
\(3x^2 -8x +5 = 5x^2\\\\5x^2 - 3x^2 + 8x -5 =0\\\\2x^2 +8x -5 = 0\\\\\)
a = 2, b = 8, c = -5
\(x = \frac{-b \pm \sqrt{b^2 -4ac} }{2a}\\\\x = \frac{-8 \pm \sqrt{8^2 - ( 4 \times 2 \times (-5))} }{2 \times 2}\\\\x = \frac{-8 \pm \sqrt{64 +40} }{4}\\\\x = \frac{-8 + \sqrt{64 +40} }{4} \ , \ x = \frac{-8 - \sqrt{64 +40} }{4}\\\\x = \frac{-8 + \sqrt{104} }{4} \ , \ x = \frac{-8 - \sqrt{104} }{4}\\\\x = \frac{-8 + \sqrt{4 \times 26} }{4} \ , \ x = \frac{-8 - \sqrt{4 \times 26} }{4}\\\\x = \frac{-8 +2 \sqrt{26} }{4} \ , \ x = \frac{-8 - 2\sqrt{26} }{4}\\\\\)
\(x = \frac{-4 + \sqrt{26} }{2} \ , \ x = \frac{-4 - \sqrt{26} }{2}\)
Mr kuldeep bought 7½ kg of and Mr Rajesh bought 5¾ kg of rice .who bought more rice and by how much.
Answers
Mr. Kuldeep bought more rice than Mr. Rajesh by 1¾ kg, or 1.75 kg more than Mr. Rajesh.
Mr. Kuldeep bought 7½ kg of rice and Mr. Rajesh bought 5¾ kg of rice. To find out who bought more rice and by how much, we need to compare the two quantities.
First, let's convert the mixed numbers into improper fractions:
7½ kg = (7 x 2 + 1)/2 = 15/2 kg
5¾ kg = (5 x 4 + 3)/4 = 23/4 kg
Now, let's compare the two fractions:
15/2 kg > 23/4 kg
Therefore, Mr. Kuldeep bought more rice than Mr. Rajesh.
To find out by how much, we need to subtract the smaller quantity from the larger one:
15/2 kg - 23/4 kg = (30 - 23)/4 kg = 7/4 kg
So, Mr. Kuldeep bought 7/4 kg or 1¾ kg more rice than Mr. Rajesh. In conclusion, Mr. Kuldeep bought more rice than Mr. Rajesh by 1¾ kg.
Here to learn more about Fractions at the link https://brainly.com/question/78672
#SPJ11
Which of the following best explains the value of Sine StartFraction pi Over 3 EndFraction on the unit circle below?
A unit circle is shown. A radius with length 1 has an angle measure of StartFraction pi Over 3 EndFraction
sine StartFraction pi Over 3 EndFraction = StartFraction opposite Over hypotenuse EndFractionEquals StartFraction opposite Over 1 EndFraction Equals opposite
The length opposite the angle is the vertical distance from the x-axis on the graph.
sine StartFraction pi Over 3 EndFraction = StartFraction adjacent Over hypotenuse EndFraction = StartFraction adjacent Over 1 EndFraction Equals adjacent
The length adjacent to the angle is the vertical distance from the x-axis on the graph.
Sine StartFraction pi Over 3 EndFraction = StartFraction opposite Over hypotenuse EndFraction = StartFraction opposite Over 1 EndFraction Equals opposite
The length opposite the angle is the horizontal distance from the y-axis on the graph.
Sine StartFraction pi Over 3 EndFraction = StartFraction adjacent Over hypotenuse EndFraction = StartFraction adjacent Over 1 EndFraction Equals adjacent
The length adjacent to the angle is the horizontal distance from the y-axis on the graph.
Answers
Answer:
a. sine StartFraction pi Over 3 EndFraction = StartFraction opposite Over hypotenuse EndFractionEquals StartFraction opposite Over 1 EndFraction Equals opposite
The length opposite the angle is the vertical distance from the x-axis on the graph.
Step-by-step explanation:
sin (π/3) = opposite/hypotenuse = opposite/1; The length opposite the angle is the vertical distance from the x-axis on the graph.
What is the trigonometric ratio of unit circle?
Unit circle is a circle centered at the origin, (0,0) with radius(r) i.,e r= 1.
The angle π/3 forms an arc of length S and the x-axis and y-axis divide the coordinate plane and the unit circle as it is centered at (0.0).
Also, the terminal side intersect the circle at (x, y). Thus;
sin (π/3) = opposite/hypotenuse = opposite/1
Thus;
sin (π/3) = opposite
Also, the length opposite the angle is the vertical distance from the x-axis on the graph.
Read more about Unit circle at; https://brainly.com/question/4637991
use simpson's rule with n=4 to approximate the solution to part b at x=0.5 to three decimal places.
Answers
Using the value of ∫01x3+1dx obtained above, we can approximate the value of∫0.50x3+1dx as:Simpson's Rule ∫abf(x)dx≈b−a3n[f(a)+2∑i=12n−1f(ai)+4∑i=14n−1f(xi)+f(b)]≈15[0+2{(13)3+1}+4{(14)3+1}+13+3]≈0.7828Therefore, the solution to part b at x=0.5 to three decimal places is approximately equal to 0.7828.
The solution to part b at x
=0.5 to three decimal places using Simpson's Rule with n
=4 is given as follows:Approximate the value of∫01x3+1dx, with Simpson's Rule using n
=4 subintervals.Simpson's Rule formula for integrating a function, f(x), with n subintervals is given as:Simpson's Rule ∫abf(x)dx≈b−a3n[f(a)+2∑i
=12n−1f(ai)+4∑i
=14n−1f(xi)+f(b)]where h
=(b−a)n and xi
=a+ih for i
=1,2,3,...,n.Substituting a
=0, b=1, f(x)
=x3+1, and n
=4 in Simpson's Rule formula:∫01x3+1dx≈14[0+2{(13)3+1+(23)3+1}+4{(14)3+1+(34)3+1}+13+3]≈1.1354The value of ∫01x3+1dx is approximately equal to 1.1354, using Simpson's Rule with n
=4 subintervals. We want to approximate the solution to part b at x
=0.5 to three decimal places. Using the value of ∫01x3+1dx obtained above, we can approximate the value of∫0.50x3+1dx as:Simpson's Rule ∫abf(x)dx≈b−a3n[f(a)+2∑i
=12n−1f(ai)+4∑i
=14n−1f(xi)+f(b)]≈15[0+2{(13)3+1}+4{(14)3+1}+13+3]≈0.7828Therefore, the solution to part b at x
=0.5 to three decimal places is approximately equal to 0.7828.
To know more about approximately visit:
https://brainly.com/question/31695967
#SPJ11
A project has four major activities. Activity A precedes activity B, activity C precedes activity D. 3-point estimates for activities are A(5, 10, 15 ), B( 5.5, 11, 16.5 ), C( 4, 4, 4 ), D( 3, 3, 3 ) weeks. What probability would you assign to a project duration of more than 21 weeks?
Answers
Note that the probability of a project duration of morethan 21 weeks is 16.60%..
How is this so ?The expected duration of each activity is -
A - (5 + 4*10 + 15) / 6 = 10 weeksB - (5.5 + 4*11 + 16.5) / 6 = 11 weeksC - (4 + 4*4 + 4) / 6 = 4 weeksD - (3 + 4*3 + 3) / 6 = 3 weeksThe critical path is A-B, with a duration of 21 weeks. The probability of the project taking more than 21 weeks is therefore the probability that at least one activity on the critical path takes longer than its expected duration.
The variance of each activity is -
A - (15 - 10)² = 25B - (16.5 - 11)² = 22.5C - (4 - 4)² = 0D - (3 - 3)² = 0The standard deviation of each activity is the square root of its variance -
* A - √(25) = 5
* B - √(22.5) = 4.743416490294949
* C - √(0) = 0
* D - √(0) = 0
The expected duration of the project is 21 weeks, with a standard deviation of 7.211102550927734 weeks. The probability of the project taking more than 28 weeks is therefore -
P(X > 28) = 1 - P(X <= 28)
= 1 - P(Z <= (28 - 21) / 7.211102550927734)
= 1 - P(Z <= 0.9722222222222222)
= 1 - 0.8340454574838693
= 0.1659545425161307
Therefore, the probability of the project taking more than 28 weeks is 16.59545425161307%.
≈ 16.60%
Learn more about probability at:
https://brainly.com/question/13604758
#SPJ1
construct a right-angled triangle ABC where angle A =90 degree , BC= 4.5cm and AC= 7cm. please ans fast........ Very urgent. Pls don't give wrong answers
Answers
Answer and Step-by-step explanation: The described right triangle is in the attachment.
As it is shown, AC is the hypotenuse and BC and AB are the sides, so use Pytagorean Theorem to find the unknown measure:
AC² = AB² + BC²
\(AB^{2} = AC^{2}-BC^{2}\)
\(AB =\sqrt{AC^{2}-BC^{2}}\)
\(AB =\sqrt{7^{2}-4.5^{2}}\)
\(AB =\sqrt{28.75}\)
AB = 5.4
Then, right triangle ABC measures:
AB = 5.4cm
BC = 4.5cm
AC = 7cm

can someone answer this question really quick
Simplify the expression by combining like terms.
43a−12b+13a+52b
Enter your answer as an expression, like this: 42x+53
Answers
Answer:
56a+40b
Step-by-step explanation:
43a plus 13a is 56a, -12b + 52b is 40b, together it's 56a+40b
Given that b(x) = x to the power of 3 complete the steps to determine the vale b(2)
Answers
Answer:
8
Step-by-step explanation:
equation: b(x) = x³
b(2) means x = 2, b(2) = (2)³
2³ = 2 x 2 x 2 = 8
Learn more about Functions here: brainly.com/question/1821791
What is 9.9581 rounded to the nearest thousandth?
Answers
Answer:
9.958
Step-by-step explanation:
The thousandths spot is where the 8 is so you round 8 with the number behind it 1. Since 1 is below 5, you keep 8 the same and get rid of the 1.
Answer:
9.958
Step-by-step explanation:
find the number in the thousands place, 8 and then look 1 place to the right for the rounding digit 1. Round up if this number is greater than or equal to 5 and round down if it is less then 5.
Please help,
Will mark as brainliest

Answers
Answer: D
Step-by-step explanation:
5 x 3 = 15
8 x 3 = 24
the multipliers are both 3
so they are "similar shapes".
The other options don't have the same multipliers so they aren't right :)
PLEASE ANSWER THESE TWO GEOMETRY QUESTIONS ASAP FOR ME PLEASE!!

Answers
Answer:
~101.5 (area of the shaded area in upper figure)
and
~54.4 (area of the shaded area in lower figure)
Step-by-step explanation:
I attached an image for clarification (please see).
The same approach can be applied to solve these two problems.
As seen in attached image, the shaded area of the 1st figure is the sum of the area of a regular triangle and 3 equal portions.
The area of the regular triangle with side = 12 is:
A1 = side^2 x sqrt(3)/4 = 12^2 x sqrt(3)/4 = 36sqrt(3)
The area of the regular triangle + the area of a portion is:
A2 = pi x radius^2 x (pi/3)/(2pi) = pi x 12^2 x (1/6) = 24pi
=> The area of a porition is:
A3 = A2 - A1 = 24pi - 36sqrt(3)
=> Area of the shade area:
A4 = A1 + 3 x A3 = 36sqrt(3) + 3 x (24pi - 36sqrt(3)) = ~101.5
**************************
For the second figure, the shaded area could be divided into 6 equal parts, each part is inside a regular triangle and is calculated by:
A = the area of the regular triangle - the area of 2 equal portions (white color).
The area of the regular triangle with side = 6 is:
A1 = side^2 x sqrt(3)/4 = 6^2 x sqrt(3)/4 = 9sqrt(3)
The area of the regular triangle + the area of a portion is:
A2 = pi x radius^2 x (pi/3)/(2pi) = pi x 6^2 x (1/6) = 6pi
=> The area of a porition is:
A3 = A2 - A1 = 6pi - 9sqrt(3)
=> Area of a part (including the regular triangle and excluding 2 equal portions):
A4 = A1 - 2 x A3 = 9sqrt(3) - 2 x (6pi - 9sqrt(3))
=> Area of shaded area:
A5 = 6 x A4 = 6 x [9sqrt(3) - 2 x (6pi - 9sqrt(3)) ] =~54.4

The ________ for a point is the number of standard errors a point is away from the mean. Group of answer choices z-value coefficient of variation variance standard deviation
Answers
The term you are looking for is the "z-value." The z-value for a point is the number of standard errors a point is away from the mean.
The z-value for a point is the number of standard errors a point is away from the mean. This is a long answer but it accurately explains the concept.
The z-value is a measure of how many standard deviations a particular observation or data point is away from the mean. It is calculated by subtracting the mean from the value and then dividing the result by the standard deviation. By doing this, we can determine whether a particular observation is within the normal range or if it is an outlier. The z-value can also be used to compare observations from different data sets as it takes into account the variability of the data.Therefore, the z-value is an important statistical tool that helps us to interpret and analyze data.Thus, the term you are looking for is the "z-value." The z-value for a point is the number of standard errors a point is away from the mean.Know more about the z-value
https://brainly.com/question/25638875
#SPJ11
What is the domain of G
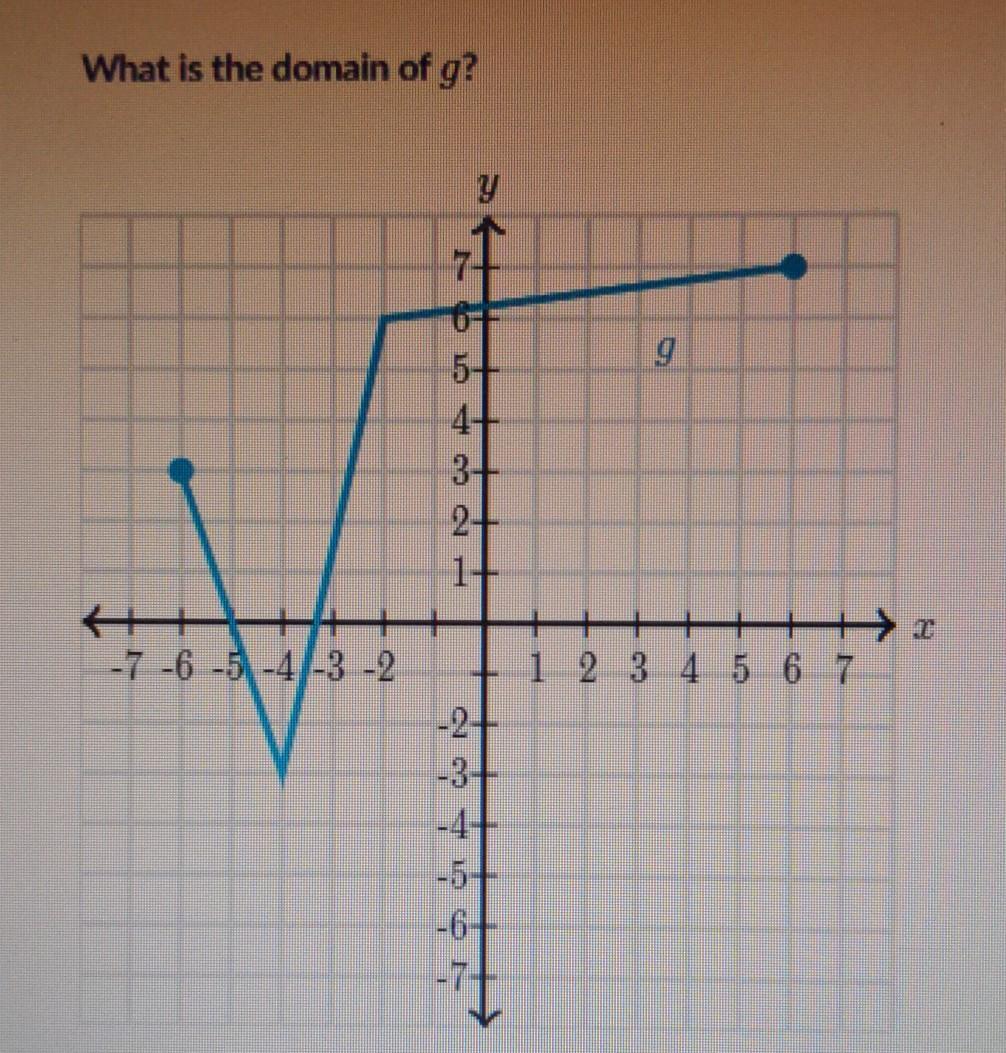
Answers
Answer:
D: {-6, 6}
Step-by-step explanation:
The domain are all the possible values for x. For this graph in the x-position, it starts from -6 to +6. Therefore, the domain will be {-6,6}.
Answer:
\(-6\leq x\leq 6\)
\(x\) ∈ \([-6, 6]\)
Step-by-step explanation:
The domain is the set of all numbers for which a function is defined. As one can see on the given graph, the function spans between the numbers (-6) and (6). Therefore, the function is defined between the numbers (-6) and (6). The closed dots on either end of the function signify that the function includes these values. Thus, the domain of the function is as follows:
(\(-6\leq x\leq 6\))
In set notation,
(\(x\) ∈ \([-6, 6]\))
What is the positive solution of |3 x+8|=19 ?
Answers
The positive solution of the equation |3x + 8| = 19 is x = 11/3. It is obtained by considering two cases and solving for x in each case.
To find the positive solution of the equation |3x + 8| = 19, we can consider two cases:
Case 1: (3x + 8) is positive
If (3x + 8) is positive, we have:
3x + 8 = 19
Solving this equation for x:
3x = 19 - 8
3x = 11
x = 11/3
Case 2: (3x + 8) is negative
If (3x + 8) is negative, we have:
-(3x + 8) = 19
Solving this equation for x:
3x + 8 = -19
3x = -19 - 8
3x = -27
x = -27/3
x = -9
Since we are looking for a positive solution by applying the arithmetic operations, we take the solution from Case 1:
x = 11/3
Therefore, the positive solution of the equation |3x + 8| = 19 is x = 11/3.
To learn more about arithmetic operations visit:
https://brainly.com/question/30553381
#SPJ11
In a right-angled triangle ABC, if angle B = 90°, then which of the
following is true?
(a) AB² = BC² + AC² (b) AC² = AB² + BC²
(c) AB = BC + AC (d) AC = AB + BC
Answers
If angle B is 90, then using Pythagoras' theorem AC² = AB² + BC²(option B)
What is Pythagoras theorem?The Pythagoras theorem which is also referred to as the Pythagorean theorem explains the relationship between the three sides of a right-angled triangle. Pythagoras' theorem, states that in a right-angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides of a triangle.
In Triangle ABC , if B is 90, it shows that the triangle is a right-angled triangle, therefore Pythagoras' theorem can be applied. line AC is the longest side ( hypotenuse) and line AB and BC are the two adjacent sides thereforeAC² = AB² + BC²
learn more about Pythagoras theorem from
https://brainly.com/question/654982
#SPJ1
