P( B
~
)=1/4 and P(A∣B)=1/2, what is P(A∩B) ?
Answers
The probability of the intersection of events A and B, P(A∩B), can be determined using conditional probability and the complement rule, resulting in a probability of 1/8.
To find P(A∩B), we can use the formula for conditional probability: P(A∣B) = P(A∩B) / P(B). Rearranging the formula, we have P(A∩B) = P(A∣B) * P(B). Given that P(A∣B) = 1/2, we substitute this value into the equation. Now, to calculate P(B), we can use the complement rule, which states that P(B) = 1 - P(B~). Given that P(B~) = 1/4, we subtract this value from 1 to find P(B) = 3/4. Plugging in the values, we get P(A∩B) = (1/2) * (3/4) = 3/8. Thus, the probability of the intersection of events A and B is 3/8 or 0.375.
Learn more about probability : brainly.com/question/31828911
#SPJ11
Related Questions
Sketch a graph of the polynomial function f(x) = –x3 + 5x2 – 2x – 8. Use the graph to complete the following:f is __________ on the intervals (–∞, 1/3) and (3, ∞)f is __________ on the interval (1/3, 3)f is __________ on the intervals (–∞, -1) and (2, 4)
Answers
To sketch the graph, we need to find the x-intercepts and y-intercepts.
To find the x-intercepts we solve the equation when y = 0.
That is
\(-x^3+5x^2-2x-8=0\)\(\begin{gathered} f(-1)=-(-1)^3+5(-1)^2-2(-1)-8=1+5+2-8=0 \\ \text{Hence} \\ x=-1\text{ is a zero of f(x)} \\ \Rightarrow\text{ x+1 is a factor of f(x)} \end{gathered}\)Next, we find the result of :
\(\frac{f(x)}{x+1}\)\(\begin{gathered} So \\ \frac{-x^3+5x^2-2x-8}{x+1}=-x^2+6x-8 \end{gathered}\)Now we solve
\(\begin{gathered} -x^2+6x-8=0 \\ \Rightarrow-x^2+2x+4x-8=0 \\ \Rightarrow-x(x-2)+4(x-2)=0 \\ \Rightarrow(4-x)(x-2)=0 \\ \Rightarrow x=4\text{ or 2} \end{gathered}\)So the zeros of f(x) are -1, 2, and 4
Next, we find the stationary points.
\(\begin{gathered} \frac{df(x)}{dx}=-3x^2+10x-2 \\ \text{When }\frac{df(x)}{dx}=0,\text{ we have} \end{gathered}\)\(\begin{gathered} -3x^2+10x-2=0 \\ \text{Dividing through by -3 we have} \\ x^2-\frac{10}{3}x+\frac{2}{3}=0 \end{gathered}\)\(\begin{gathered} (x-\frac{5}{3})^2-(-\frac{5}{3})^2-2=0 \\ \Rightarrow(x-\frac{5}{3})^2=2+\frac{25}{9}=\frac{43}{9} \\ \Rightarrow x=\frac{5\pm\sqrt[]{43}}{3} \\ \Rightarrow x=2.55\text{ or }0.78 \end{gathered}\)\(\frac{d\frac{df(x)}{dx}}{dx}=-6x+10\)At x = 2.55
\(\frac{d\frac{df(x)}{dx}}{dx}=-6(2.55)+10=-5.3<0\)Hence we have a maximum point at x = 2.55
\(\frac{d\frac{df(x)}{dx}}{dx}=-6(0.78)+10=5.32>0\)Hence, there is a minimum point at x = 0.78
\(\begin{gathered} f(0.78)\text{ = }-6.99 \\ f(2.550=2.83 \end{gathered}\)\(\begin{gathered} To\text{ check the intervals where the function increasing or decreasing} \\ \text{For x < 0.78 } \\ \frac{df(x)}{dx}=(x-0.78)(x-2.83)\text{ is positive} \\ \text{For 0.78 < x < 2.83 } \\ \frac{df(x)}{dx}=(x-0.78)(x-2.83)\text{ is negative} \\ \text{For x > 2.83} \\ \frac{df(x)}{dx}=(x-0.78)(x-2.83)\text{ is positive} \end{gathered}\)This implies that
f is increasing on the intervals (–∞, 1/3) and (3, ∞)


What is the geometric mean between 6 and 12?
Answers
Answer:the geometric mean is the product of all the numbers in a set, with the root of how many numbers there are.
here, there are two numbers, so a square root is used.
geometric mean of
3
and
12
:
√
3
⋅
12
3
⋅
12
=
36
√
36
=
6
the value of the geometric mean of
3
and
12
is
6
.
Step-by-step explanation:
4) Gus and Cal go bowling every week. Gus's scores are normally distributed with a mean of 175 pins and a standard deviation of 30 pins. Cal's scores are normally distributed with a mean of 150 pins and a standard deviation of 40 pins. Assume that their scores in any given game are independent. Let G be Gus's score in a random game, C be Cal's score in a random game, and D be the difference between Gus's and Cal's scores where D = G - C What is the probability that Gus will knock down more pins than Cal?
Answers
There is a 0.6915 = 69.15% probability that Gus will knock down more pins than Cal.
How to obtain probabilities using the normal distribution?The z-score of a measure X of a normally distributed variable that has mean represented by \(\mu\) and standard deviation represented by \(\sigma\) is obtained by the equation presented as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score represents how many standard deviations the measure X is above or below the mean of the distribution of the data-set, depending if the obtained z-score is positive(above the mean) or negative(below the mean).The z-score table is used to obtain the p-value of the z-score, and it represents the percentile of the measure X in the distribution.When two variables are subtracted, we have that:
The mean is the subtraction of the means.The standard deviation is the square root of the sum of the variances.Hence the mean and the standard deviation for D are given as follows:
\(\mu = 175 - 150 = 25\).\(\sigma = \sqrt{30^2 + 40^2} = 50\)The probability that Gus will knock down more pins than Cal ia P(D > 0), which is one subtracted by the p-value of Z when X = 0, hence:
Z = (0 - 25)/50
Z = -0.5
Z = -0.5 has a p-value of 0.3085.
Hence:
1 - 0.3085 = 0.6915 = 69.15%.
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ1
5. a building has 6 homes per floor and 3 floors. on the first floor, there are 4 penguins per home. on the second and third floors, there are 3 penguins per home.
which equation can we use to find, p, the total number of penguins living in the building?
(a) 3.6. (4+3) =p
(b) (4.6) + (3.6) +(3.6) =p
(c) (4.6) + (3.6). 3 =p
Answers
The correct equation to find the total number of penguins living in the building is option (b): (4.6) + (3.6) + (3.6) = p
Let's break down the equation: (4.6) represents the number of penguins per home on the first floor, multiplied by the total number of homes on the first floor (6 homes per floor). (3.6) represents the number of penguins per home on the second floor, multiplied by the total number of homes on the second floor (6 homes per floor).
(3.6) represents the number of penguins per home on the third floor, multiplied by the total number of homes on the third floor (6 homes per floor). By adding these three terms together, we get the total number of penguins, represented by p.
Therefore, option (b) is the correct equation to find the total number of penguins living in the building.
To learn more about Total click here: brainly.com/question/24873526
#SPJ11
Solve for b
a) 2b x 3 = 6 c) 6 + 7b = 41
b) 32 - 3b = 2 d) 100/ 5b = 2
Answers
a) The solution for b in the equation 2b × 3 = 6 is b = 1.
b) The solution for b in the equation 32 - 3b = 2 is b = 10.
c) The solution for b in the equation 6 + 7b = 41 is b = 5.
d) The solution for b in the equation 100/5b = 2 is b = 10.
a) To solve for b in the equation 2b × 3 = 6, we can start by dividing both sides of the equation by 2 to isolate b.
2b × 3 = 6
(2b × 3) / 2 = 6 / 2
3b = 3
b = 3/3
b = 1
Therefore, the solution for b in the equation 2b × 3 = 6 is b = 1.
c) To solve for b in the equation 6 + 7b = 41, we can start by subtracting 6 from both sides of the equation to isolate the term with b.
6 + 7b - 6 = 41 - 6
7b = 35
b = 35/7
b = 5
Therefore, the solution for b in the equation 6 + 7b = 41 is b = 5.
b) To solve for b in the equation 32 - 3b = 2, we can start by subtracting 32 from both sides of the equation to isolate the term with b.
32 - 3b - 32 = 2 - 32
-3b = -30
b = (-30)/(-3)
b = 10
Therefore, the solution for b in the equation 32 - 3b = 2 is b = 10.
d) To solve for b in the equation 100/5b = 2, we can start by multiplying both sides of the equation by 5b to isolate the variable.
(100/5b) × 5b = 2 × 5b
100 = 10b
b = 100/10
b = 10.
Therefore, the solution for b in the equation 100/5b = 2 is b = 10.
In summary, the solutions for b in the given equations are:
a) b = 1
c) b = 5
b) b = 10
d) b = 10
For similar question on equation.
https://brainly.com/question/30451972
#SPJ8
How to solve the blank

Answers
Answer:
blank = - 3
Step-by-step explanation:
let x represent the blanks , then
\(\frac{2}{3}\) (\(\frac{9}{5}\) + x) = \(\frac{2}{5}\) x + \(\frac{2}{5}\)
multiply through by 15 ( the LCM of 3 and 5 ) to clear the fractions
10(\(\frac{9}{5}\) + x) = 6x + 6 ← distribute parenthesis on left side
\(\frac{90}{5}\) + 10x = 6x + 6
18 + 10x = 6x + 6 ( subtract 6x from both sides )
18 + 4x = 6 ( subtract 18 from both sides )
4x = - 12 ( divide both sides by 4 )
x = - 3
00 Estimate (2n + 1)-6 correct to five decimal places. ) n = 1 + Find the radius of convergence and interval of convergence of the series. (-1)"" (8n)!"
Answers
The radius of convergence (R) is infinite, indicating that the series converges for all values of x. Therefore, the interval of convergence is (-∞, +∞).
To estimate the value of the expression (2n + 1)^-6, we can substitute the given value n = 1 into the expression and evaluate it. (2n + 1)^-6 = (2(1) + 1)^-6 = (2 + 1)^-6 = 3^-6. Calculating the value: 3^-6 = 1/(3^6) = 1/729. So, the expression (2n + 1)^-6, when n = 1, is approximately equal to 0.001371742112.
Regarding the series (-1)^(8n)/(8n)!, let's analyze its convergence properties. The radius of convergence (R) of a power series is determined by the formula: 1/R = Lim (n -> ∞) |a(n+1)/a(n)|. In this case, a(n) is the term (-1)^(8n)/(8n)!. To simplify the analysis, let's consider the absolute value of a(n): |a(n)| = |(-1)^(8n)/(8n)!| = 1/(8n)!
Now, let's calculate the ratio |a(n+1)/a(n)|: |a(n+1)/a(n)| = |(-1)^(8(n+1))/(8(n+1))!| / |(-1)^(8n)/(8n)!| = |(-1)^8(n+1)/(8(n+1))!| * |(8n)!/(-1)^(8n)| = 1/(8(n+1)). Taking the limit as n approaches infinity: Lim (n -> ∞) |a(n+1)/a(n)| = Lim (n -> ∞) (1/(8(n+1))) = 0. Since the limit is 0, the radius of convergence (R) is infinite, indicating that the series converges for all values of x. Therefore, the interval of convergence is (-∞, +∞).
To learn more about convergence, click here: brainly.com/question/31440916
#SPJ11
HELPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP TY

Answers
Answer:
13m+8
Step-by-step explanation:
(20m+3)+(-7m+5)
(20m-7m)+(3+5)
13m+8
Answer:
B.) 13m+8
Step-by-step explanation:
Hope this helps and have a great day! :)(a) Derive the class equation of a finite group G.
(b) Prove that a Sylow p-subgroup of a finite group G is normal if and only if it is unique.
Answers
a) The center of G and determining the distinct conjugacy classes, we can calculate the class equation of the finite group G.
b) We have shown both implications: if a Sylow p-subgroup is normal, then it is unique, and if it is unique, then it is normal.
(a) Deriving the class equation of a finite group G involves partitioning the group into conjugacy classes. Conjugacy classes are sets of elements in the group that are related by conjugation, where two elements a and b are conjugate if there exists an element g in G such that b = gag^(-1).
To derive the class equation, we start by considering the group G and its conjugacy classes. Let [a] denote the conjugacy class containing the element a. The class equation is given by:
|G| = |Z(G)| + ∑ |[a]|
where |G| is the order of the group G, |Z(G)| is the order of the center of G (the set of elements that commute with all other elements in G), and the summation is taken over all distinct conjugacy classes [a].
The center of a group, Z(G), is the set of elements that commute with all other elements in G. It can be written as:
Z(G) = {z in G | gz = zg for all g in G}
The order of Z(G), denoted |Z(G)|, is the number of elements in the center of G.
The conjugacy classes [a] can be determined by finding representatives from each class. A representative of a conjugacy class is an element that cannot be written as a conjugate of any other element in the class. The number of distinct conjugacy classes is equal to the number of distinct representatives.
By finding the center of G and determining the distinct conjugacy classes, we can calculate the class equation of the finite group G.
(b) To prove that a Sylow p-subgroup of a finite group G is normal if and only if it is unique, we need to show two implications: if it is normal, then it is unique, and if it is unique, then it is normal.
If a Sylow p-subgroup is normal, then it is unique:
Assume that P is a normal Sylow p-subgroup of G. Let Q be another Sylow p-subgroup of G. Since P is normal, P is a subgroup of the normalizer of P in G, denoted N_G(P). Since Q is also a Sylow p-subgroup, Q is a subgroup of the normalizer of Q in G, denoted N_G(Q). Since the normalizer is a subgroup of G, we have P ⊆ N_G(P) ⊆ G and Q ⊆ N_G(Q) ⊆ G. Since P and Q are both Sylow p-subgroups, they have the same order, which implies |P| = |Q|. However, since P and Q are subgroups of G with the same order and P is normal, P = N_G(P) = Q. Hence, if a Sylow p-subgroup is normal, it is unique.
If a Sylow p-subgroup is unique, then it is normal:
Assume that P is a unique Sylow p-subgroup of G. Let Q be any Sylow p-subgroup of G. Since P is unique, P = Q. Therefore, P is equal to any Sylow p-subgroup of G, including Q. Hence, P is normal.
Therefore, we have shown both implications: if a Sylow p-subgroup is normal, then it is unique, and if it is unique, then it is normal.
for such more question on distinct conjugacy
https://brainly.com/question/11583754
#SPJ8
solve 1/2 x + 3 8/7
B) x 7/20
D) x > 20/7
Answers
Answer:
B.
Step-by-step explanation:
I just took the test.
Brainliest?
The productivity, P , of a worker in a factory can be modeled by the function p\(x)\ = -2x^2 + 24x, where x is the number of hours worked. How many hours have been worked when productivity is at 0 ?
Answers
According to the quadratic equation, it is found that 12 hours have been worked when productivity is at 0.
What is the quadratic equation for the worker's productivity?It is given by:
P(x) = -2x² + 24x
It is of zero when:
P(x) = 0.
Hence:
-2x² + 24x = 0
2x(-x + 12) = 0
We want the non-zero result, hence:
-x + 12 = 0 -> x = 12
12 hours have been worked when productivity is at 0.
More can be learned about quadratic equations at https://brainly.com/question/24737967
a researcher wishes to estimate the proportion of households that have broadband internet access. what size sample should be obtained if she wishes the estimate to be within 0.03 with 99% confidence if (a) she uses a 2009 estimate of 0.635 obtained from the national telecommunications and information administration? (b) she does not use any prior estimates
Answers
(a) The researcher should obtain a sample size of 1,068 households to estimate the proportion of households with broadband internet access within 0.03 with 99% confidence, assuming a prior estimate of 0.635 from 2009.
(b) If the researcher does not use any prior estimates, she can use a conservative estimate of 0.5 for the proportion of households with broadband internet access, as this value maximizes the sample size required for a given level of precision and confidence. With this assumption, the researcher should obtain a sample size of 1,068 households to estimate the proportion of households with broadband internet access within 0.03 with 99% confidence. It is important to note that if the true proportion is significantly different from 0.5, the required sample size may be higher or lower than this estimate. Additionally, the researcher should consider other factors such as the cost and feasibility of obtaining a sample of this size.
Learn more about researcher here: brainly.com/question/24174276
#SPJ11
given the if/else statement: if (a < 5) b = 12; else d = 30; which of the following performs the same operation?
Answers
The equivalent operation is: b = (a < 5) ? 12 : (d = 30);
The original if/else statement is:
if (a < 5)
b = 12;
else
d = 30;
In this statement, the condition (a < 5) is evaluated. If the condition is true (i.e., if the value of a is less than 5), then the statement b = 12; is executed. Otherwise, if the condition is false (i.e., if the value of a is greater than or equal to 5), then the statement d = 30; is executed.
The equivalent operation using the conditional (ternary) operator is:
b = (a < 5) ? 12 : d = 30;
In this statement, the condition (a < 5) is evaluated. If the condition is true, the value 12 is assigned to b. This is indicated by ? in the statement. The : separates the true and false cases.
If the condition is false (i.e., if the value of a is greater than or equal to 5), the value 30 is assigned to d. This is the value assigned after the : in the statement.
The ternary operator statement (a < 5) ? 12 : d = 30; achieves the same outcome as the original if/else statement, providing an alternative way to write the logic based on the condition a < 5.
Learn more about conditionals here:
https://brainly.com/question/17388479
#SPJ8
What is the answer to 3(2x+5)=3x+4x
Answers
6x+15=3x+4x
6x+15=7x
15=7x-6x
15=1x
x=15/1
x=15
3(30+5)=45+60
3(30+5)=105
45+60=105
so x=15
BRAINLIEST PERSON WHO GETS IT
Nyoko wrote these two questions.
Equation 1: 6x-5+2x = 4(2x-1) - 1
Equation 2: 3x +7 = bx+7
Part A
Nyoko says that Equation 1 has one solution. Do you agree with her? Explain your reasonings.
Part B
Can Nyoko find a value for b in Equation 2 so that the equation has no solutions? Explain Your REASONING!
Answers
a) The equation 1 has an infinite number of solutions, as both linear functions have the same slope and internet, hence Nyoko is incorrect.
b) Nyoko cannot find a value of b so that the equation has no solutions.
How to solve the equations?The equation 1 is given as follows:
6x - 5 + 2x = 4(2x - 1) - 1.
Combining the like terms and applying the distributive property, the simplified equations are given as follows:
8x - 5 = 8x - 4 - 1
8x - 5 = 8x - 5.
As they are linear functions with the same slope and intercept, the number of soltuions is of infinity.
The equation 2 is given as follows:
3x + 7 = bx + 7.
A system of linear equations will have zero solutions when:
The equations have the same slope.The equations have different intercepts.As they have the same intercept for this problem, it is not possible to attribute a value of b such that the equation will have no solution.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
Bruce scored 22 out of 25 on his math test, What percent did he earn? What letter grade did he get on the test?
Answers
Answer:
Bruce earned an 88%. Depending on what school district he is from, it is an A or a B.
Step-by-step explanation:
Partition a line segment in the given ratio.
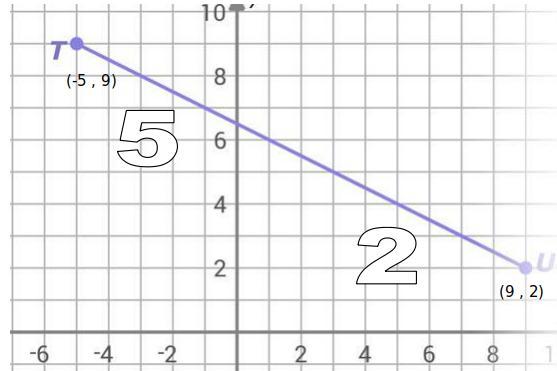
Point V lies on TU such that TV:UV is 5:2. Graph V.

Answers
Check the picture below.
\(\textit{internal division of a line segment using ratios} \\\\\\ T(-5,9)\qquad U(9,2)\qquad \qquad \stackrel{\textit{ratio from T to U}}{5:2} \\\\\\ \cfrac{T\underline{V}}{\underline{V} U} = \cfrac{5}{2}\implies \cfrac{T}{U} = \cfrac{5}{2}\implies 2T=5U\implies 2(-5,9)=5(9,2)\)
\((\stackrel{x}{-10}~~,~~ \stackrel{y}{18})=(\stackrel{x}{45}~~,~~ \stackrel{y}{10}) \implies V=\underset{\textit{sum of the ratios}}{\left( \cfrac{\stackrel{\textit{sum of x's}}{-10 +45}}{5+2}~~,~~\cfrac{\stackrel{\textit{sum of y's}}{18 +10}}{5+2} \right)} \\\\\\ V=\left( \cfrac{ 35 }{ 7 }~~,~~\cfrac{ 28}{ 7 } \right)\implies {\Large \begin{array}{llll} V=(5~~,~~4) \end{array}}\)
Max must take 10 steps to go the same distance as three of his dad's steps. His dad takes 30 steps to walk down the hall. How many steps must Max take to walk down the same hall?
Answers
Max : 10 steps : Dad: 3 steps.
So it you multiply those each by ten, you get
100 steps : 30 steps.
30 Dad steps is 100 Max steps, so you get the answer, which is 100!
The steps taken by Max is 100.
what is arithmetic operators?A mathematical function that performs a calculation on two operands is known as an arithmetic operator. Common arithmetic makes use of them, and the majority of computer languages include a set of such operators that can be used in equations to carry out a variety of sequential calculations.
Given
steps taken by Max = 10
Steps taken by his Dad = 3
both steps of Dad and steps of Max should be in ratio
3/10 …(1)
steps taken by his Dad = 30
let steps taken by Max = x
ratio = 30/x …..(2)
equation 1 equals equation 2
3/10 = 30/x
x = (30 x 10)/3
x = 100
Hence Max must take 100 steps.
Learn more about arithmetic operators;
https://brainly.com/question/25834626
#SPJ5
Which of these references a velocity (not speed) more than one answer 50 mph
5 mph East
5 mph
50 mph South
Answers
Answers: 5 mph East and 50 mph South
Reason
A velocity has two components: A speed and a direction.
can someone please help me answer this function please?

Answers
Answer:
B) \(x\geq0\)
Step-by-step explanation:
The domain of the square root function is all real non-negative numbers. In a numerical format that is as follows:
\(D(\sqrt{x})={[0,\infty )}\)
This is more commonly denoted as:
\(x\geq0\)
In the case of the given function:
\(g(x)=\sqrt{8x}\)
The domain is still (\(x\geq0\)) as multiplying a value by (8) does not alter this. A negative number times (8) is still negative and thus cannot be a part of the square root domain. Similarly, a positive number times (8) is still positive and remains a part of the square root domain. Moreover, (0) times (8) is still (0).
What value for x will make the equation −3x+1=2(4x−5)true?
Answers
hello please help i’ll give brainliest

Answers
Answer:
Ecosystem
Step-by-step explanation:
He is investigating both living and non living organisms.
Please help me. Thank you so much!

Answers
Answer: the answer is d. 7.2 feet
Step-by-step explanation: hope this helps!
Dilate the trapezoid using center (-3,4) and scale factor 1/2.

Answers
The coordinates of the vertices of the image of the trapezoid are A'(x, y) = (- 4, 1), B'(x, y) = (- 2, 1), C'(x, y) = (- 5 / 2, 5 / 2) and D'(x, y) = (- 7 / 2, 5 / 2).
How to find the image of a trapezoid by dilation
In this question we have a representation of a trapezoid, whose image has to be generated by a kind of rigid transformation known as dilation, whose equation is described below:
P'(x, y) = O(x, y) + k · [P(x, y) - O(x, y)]
Where:
O(x, y) - Center of dilationk - Scale factorP(x, y) - Coordinates of the original point.P'(x, y) - Coordinates of the resulting point.If we know that k = 1 / 2, A(x, y) = (- 5, - 2), B(x, y) = (- 1, - 2), C(x, y) = (- 2, 1), D(x, y) = (- 4, 1), O(x, y) = (- 3, 4), then the coordinates of the vertices of the image are:
Point A'
A'(x, y) = O(x, y) + k · [A(x, y) - O(x, y)]
A'(x, y) = (- 3, 4) + (1 / 2) · [(- 5, - 2) - (- 3, 4)]
A'(x, y) = (- 3, 4) + (1 / 2) · (- 2, - 6)
A'(x, y) = (- 3, 4) + (- 1, - 3)
A'(x, y) = (- 4, 1)
Point B'
B'(x, y) = O(x, y) + k · [B(x, y) - O(x, y)]
B'(x, y) = (- 3, 4) + (1 / 2) · [(- 1, - 2) - (- 3, 4)]
B'(x, y) = (- 3, 4) + (1 / 2) · (2, - 6)
B'(x, y) = (- 3, 4) + (1, - 3)
B'(x, y) = (- 2, 1)
Point C'
C'(x, y) = O(x, y) + k · [C(x, y) - O(x, y)]
C'(x, y) = (- 3, 4) + (1 / 2) · [(- 2, 1) - (- 3, 4)]
C'(x, y) = (- 3, 4) + (1 / 2) · (1, - 3)
C'(x, y) = (- 3, 4) + (1 / 2, - 3 / 2)
C'(x, y) = (- 5 / 2, 5 / 2)
Point D'
D'(x, y) = O(x, y) + k · [D(x, y) - O(x, y)]
D'(x, y) = (- 3, 4) + (1 / 2) · [(- 4, 1) - (- 3, 4)]
D'(x, y) = (- 3, 4) + (1 / 2) · (- 1, - 3)
D'(x, y) = (- 3, 4) + (- 1 / 2, - 3 / 2)
D'(x, y) = (- 7 / 2, 5 / 2)
To learn more on dilations: https://brainly.com/question/13176891
#SPJ1

Could really use some help pls! It's due soon!

Answers
Draw a line on y=-2 and reflect the dot on the other side. The x doesn’t change, only y changes. So only option is (2,1).
Point x is located at ( 2,5)
When reflecting across the y axis the x value remains the same.
The reflection is at y -2, from -2 to the location of z (-5) is a difference of 3 units.
Add 3 to the reflection line -2 + 3 = 1 , the new y value would be 1.
the new location would be (2,1)
I need help please i don't get this.

Answers
Answer:
22
Step-by-step explanation:
Points Y and X are are the midpoints of the segments HI and HG respectively.
Therefore,
By Mid-segment formula:
IG = 2*YX = 2* 11 = 22 units
find the sum of all positive integers less than 200 which are divisible by 3
Answers
Answer:
we will use the sum of natural number series formula
if S=1+2+3+4+n, then
S= n(n+1) ;
2
Now, sum of all +ve integers from 0 to 200 is given by
S=0+1+2+3+200
=> S=200(200+1)/2;
=>S=20100;
Sum of all +ve integers divisible by 5 is given by
R=0+5+10+15+20+25+30+200
R=5(1+2+3+4+5+6+40)
R=5*40(40+1)/2
R=4100 ;
therefore the sum of all +ve integers <200 and not divisible by 5=S-R=16000
Step-by-step explanation:
a manufacturer of potato chips would like to know whether its bag filling machine works correctly at the 411.0 gram setting. it is believed that the machine is underfilling the bags. a 35 bag sample had a mean of 406.0 grams. a level of significance of 0.05 will be used. state the hypotheses. assume the standard deviation is known to be 25.0.
Answers
Using a 35-bag sample with a mean of 406.0 grams, a known standard deviation of 25.0 grams, and a level of significance of 0.05, you can perform a one-tailed Z-test to determine whether to reject or fail to reject the null hypothesis.
To test if the potato chip manufacturer's bag filling machine is working correctly at the 411.0-gram setting, we will state the hypotheses using the given terms.
Null Hypothesis (H0): The machine fills bags correctly, with a mean weight of 411.0 grams (µ = 411.0 grams)
Alternative Hypothesis (H1): The machine is underfilling bags, with a mean weight less than 411.0 grams (µ < 411.0 grams)
To learn more about standard deviation, refer here:
https://brainly.com/question/23907081#
#SPJ11
1.8 Seats for Financial Management, Marketing and Office Practice in an examination venue of a certain TVET college are at a ratio of 4:8:10 respectively. There is proposal that to increase these seats by 26%, 50% and 60% respectively. What will the ratio of the increased seats be? Show your workings (6)
Answers
The ratio of increased seats will be 5:12:16.
What is ratio?Ratio is a comparison between two or more quantities expressed as a fraction or a set of relative quantities it is used to compare the size of one number to another or the compare changes overtime ratio can be expressed in word as fraction or decimal receiver in important concept in mathematics used to analyse data and solve problem.
This can be found by calculating the increase as a percentage of the current number of seats.
For Financial Management, the increase of 26% is calculated as (4 x 0.26) + 4 = 5.04, which rounds up to 5.
For Marketing, the increase of 50% is calculated as (8 x 0.5) + 8 = 12.
For Office Practice, the increase of 60% is calculated as (10 x 0.6) + 10 = 16.
Therefore, the ratio of the increased seats will be 5:12:16.
To know more about ratio click-
https://brainly.com/question/9017156
#SPJ1
Cual el el radio de un círculo con diámetro de 9 cm
Answers
The length of the radius with diameter 9 cm is 4.5 cm.
What is a chord of a circle?A chord of a circle refers to a line segment that connects two points on the circle's circumference. It is the longest segment that can be drawn between two points on a circle, and it divides the circle into two segments. The length of a chord is dependent on its distance from the center of the circle. When a chord passes through the center of the circle, it is referred to as the diameter and is the longest chord. On the other hand, a minor chord does not pass through the circle's center. Chords possess several properties and are utilized in numerous geometric and mathematical applications. They play a significant role in comprehending circle properties and are applicable in calculus, trigonometry, and geometry.
The question is a circle with a diameter 9 cm.
We know that diameter is the largest chord of the circle which contains the center of the circle. We also know that the line joining the center of the circle to a point on a circle is called the radius of the circle.
Hence we can see that it will be half the length of the diameter:
Radius = Diameter/2 = 9 cm/2 = 4.5cm.
To know more about chord visit:
brainly.com/question/1654080
#SPJ9
The complete question is: "What is the radius of a circle with a diameter of 9 cm?"