Omar reads 56 chapters of a book in 8 hours. What is his rate in chapters per hour?
Answers
Answer:
Omar can read 7 chapters per hour
Step-by-step explanation:
every 7 chapter counts as a hour, so by the time its 8 hours, Omar would've read 56 chapters in 8 hours
Related Questions
PLEASEEE HELP QUICK :D

Answers
Answer:
Option a!
Step-by-step explanation:
inverse means opposite:
First part of the statement:
If I studied for it
(opposite)
If I did not study for it
Second:
I did well on the exam
(opposite)
I did not do well on the exam
Hope this makes sense.
- profparis
Please show work (if needed) help ASAP

Answers
Answer:
First one is option D. Plane Bad, second one is option B. Point C
Solve for x in the diagram below.
30°
80°
2.cº
T =

Answers
100 = 5x
x = 20
Hello, there!!!!
Given that,
80°,3x° and 2x°are three angles on a st.line.
we have,
2x°+3x°+80°= 180° {The total sum of angles on a st. line is 180°}.
or, 5x°= 180°-80°
or, 5x°=100°
or, x= 100°/5
Therefore the value of x is 20°.
Hope it helps...
If a0=10 and an+1=-5an then find the value of a4
Answers
The value of a4 would be equal to -666.
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
A mathematical equation is a statement with two equal sides and an equal sign in between. An equation is, for instance, 4 + 6 = 10. Both 4 + 6 and 10 can be seen on the left and right sides of the equal sign, respectively.
Given that \(a_0=10\) and \(a_n+1=-5a_n\)
This is a recursive formula. So we can simply substitute in each value. For instance, a₂
Use the recursive definition repeatedly.
a2 = -5(6) +4 = -26
a3 = -5(-26) +4 = 134
a4 = -5(134) +4 = -666
Therefore, the value of a4 is -666
Learn more about equations here;
https://brainly.com/question/25180086
#SPJ1
through (2,4) parrallel to y=3x+
Answers
The slope y is 3x - 10.When the line to be examined's slope is known, and the provided point also serves as the y intercept.
The slope intercept form of a line's equation can be found by using this method?When the line to be examined's slope is known, and the provided point also serves as the y intercept, the slope intercept formula, y = mx + b, is utilized (0, b). B stands in for the y value of the y-intercept point in the formula.
According to question:-
In the equation of a line's slope-intercept form, y = mx + b, we get y = 3x + 2, m1 = m2 gives us y = 3x +2, and m = 3 gives us the point (2 -4) where x = 2 and y = -4.
4 6 + b deducts 6 from both sides.
-10 = b, b = -10
After all, y = 3x - 10.
The complete question is,
y=3x+2 via (2,-4) parallel to
To know more about slope visit:
brainly.com/question/3493733
#SPJ1
Add -12 + 7 5 O-5 O 19 0-19
Answers
Addition over real numerical line.
Add negative numbers -12 -5 -19 = -36
Add positive numbers +7 + 5 + 19 = 31
Now add both results -36 + 31 = -5
For the following situation, find the mean and standard deviation of the population. List all samples (with replacement) of the given size from that population. Find the mean and
standard deviation of the sampling distribution and compare them with the mean and standard deviation of the population.
The number of DVDs rented by each of three families in the past month is 2, 11, and 5. Use a sample size of 2
Answers
The correct comparison of the population and sampling distribution is A. Means are the same but the standard deviation of sampling distribution is smaller
How to find the mean and standard deviationX X^2
95 9025
96 9216
98 9604
Sum = 289 27845
n 3
The sample mean 96.33333333 SUM/n
Population mean 96.33333333 SUM/n
Sample standard dev \(1.527525232 \sqrt{((1/(n-1))(SUM(X^2)-(1/n)SUM(X)^2)}\)
Population standard dev \(1.247219129 \sqrt{((1/n)(SUM(X^2)-(1/n)SUM(X)^2)}\)
Population Mean(μ) = 96.33
Population standard deviation (σ) = 1.25
Option A) 95,96,98 and X bar = 96.33
Sampling distribution :
mean (μx = μ) = 96.33
standard deviation(σx = σ/SQRT(n)) = 1.25/SQRT(3) = 0.72
Option A) Means are the same but the standard deviation of the sampling distribution is smaller
Read more about standard deviation here:
https://brainly.com/question/24298037
#SPJ1

PLEASE HELP EASY!!!!!!

Answers
Based on the information, we can infer that the salary a worker earns depends on the hourly wage they earn. In this case we will have to multiply the value of each hour by the number of hours worked. Additionally, I would agree to have a higher minimum wage to benefit workers.
What salary will workers have in each salary?Based on the information in the graph, we can infer that workers will have wages of $5.2, $6.0, and $6.6. According to the above, the salary varies depending on the number of hours.
On the other hand, I believe that you would agree to a salary increase because this would benefit workers who would be better paid for each hour of work.
Learn more about workers in: https://brainly.com/question/30203906
#SPJ1
This graph represents the flight path of a model rocket launched in a park.
What do the key features of the curve represent in terms of the flight path of the rocket?
Chose from the drop-down to match each situation.
ill give brainlyest to the first to correctly answer this

Answers
The drop down menu is used to match each situation as below.
1. The rocket reached its maximum the x-value of the vertex
height in 5 s.
2. ground level the y-intercept
3. The rocket launcher was the y-value of the point containing
on the ground. the x-intercept on the right
4. The rocket was in the air 10 the x-intercept on the right
5. The maximum height of the the y-value of the vertex
rocket is 50 ft.
6. the time the rocket was the x-value of the point containing the
launched y-intercept
What is the key feature of the curveThe key features of the curve such as the x intercept is the point the launcher and the rocket were on ground.
The vertex is the point the rocket had the maximum and height.
Generally, the curve traces a parabolic path
Learn more about parabolic equation at
https://brainly.com/question/4061870
#SPJ1
Suppose we are minimizing the objective function value of a linear program. The feasible region is defined by 5 corner points. The objective function values at the five corner points are 4, 11, 7, 4, and 10. What type of solution do we have for this problem?.
Answers
The linear program shows that there are different attainable arrangements that accomplish the same ideal objective function value..
How to determine the solution to the objective function value of a linear programBased on the given data, since the objective function values at the five corner points are diverse, able to conclude that there's no one-of-a-kind ideal arrangement for this linear program.
The reality that there are numerous distinctive objective function values at the corner points suggests that there are numerous ideal arrangements or that the objective work isn't maximized or minimized at any of the corner points.
In this case, the linear program may have numerous ideal arrangements, showing that there are different attainable arrangements that accomplish the same ideal objective function value.
Learn more about Objective function value here:
https://brainly.com/question/14309521
#SPJ1
Zuri drove at an average speed of
50
mi/h from her home in Orlando to visit her sister in Tucson. She stayed in Tucson
10
hours, and on the trip back averaged
55
mi/h. She returned home
49
hours after leaving. How many miles is Orlando from Tucson?
a) Write an equation using the information as it is given above that can be solved to answer this question. Use
t
as your variable to represent the amount of time Zuri spent driving from Orlando to Tucson.
Equation:
b) How many miles is Orlando from Tucson?
Answer: miles
Answers
Orlando is approximately 1021.5 miles from Tucson.
a) Let's use the formula: distance = rate x time.
Let t be the time Zuri spent driving from Orlando to Tucson.
Then, the time she spent driving from Tucson to Orlando would be 49 - 10 - t = 39 - t (subtracting the time she stayed in Tucson and the time she already spent driving from Orlando to Tucson from the total time).
Using the formula, we can write two equations:
distance from Orlando to Tucson = 50t
distance from Tucson to Orlando = 55(39 - t)
The total distance traveled is the same in both directions, so we can set the two equations equal to each other and solve for t:
50t = 55(39 - t)
50t = 2145 - 55t
105t = 2145
t = 20.43
b) Now that we know the time it took for Zuri to travel from Orlando to Tucson, we can use one of the equations above to find the distance:
distance from Orlando to Tucson = 50t
distance from Orlando to Tucson = 50(20.43)
distance from Orlando to Tucson = 1021.5
Therefore, Orlando is approximately 1021.5 miles from Tucson.
To know more about Equation visit:
brainly.com/question/9312365
#SPJ1
Orlando is approximately 1021.5 miles from Tucson.
What is the linear equation?
A linear equation is defined as a function that has either one or two variables without exponents. It is a function that graphs to a straight line.
a) Let's use the formula: distance = rate x time.
Let t be the time Zuri spent driving from Orlando to Tucson.
Then, the time she spent driving from Tucson to Orlando would be 49 - 10 - t = 39 - t (subtracting the time she stayed in Tucson and the time she already spent driving from Orlando to Tucson from the total time).
Using the formula, we can write two equations:
distance from Orlando to Tucson = 50t
distance from Tucson to Orlando = 55(39 - t)
The total distance traveled is the same in both directions, so we can set the two equations equal to each other and solve for t:
50t = 55(39 - t)
50t = 2145 - 55t
105t = 2145
t = 20.43
b) Now that we know the time it took for Zuri to travel from Orlando to Tucson, we can use one of the equations above to find the distance:
distance from Orlando to Tucson = 50t
distance from Orlando to Tucson = 50(20.43)
distance from Orlando to Tucson = 1021.5
Therefore, Orlando is approximately 1021.5 miles from Tucson.
To know more about linear equations visit:
brainly.com/question/9312365
#SPJ1
Find the y-intercept of the parabola y=x^2
Answers
Hello!
The y intercept of the parabola is when one of it's function's hits/intersects the y axis. The y intercept of the parabola y = x^2 is (0,0).
You may be wondering where is that, and why is it there. Y = x^2 is a parent function.
Check the image below for better explanation from me.
(0,0) = y - intercept

Question 10
A car park has 880 parking spaces.
Some of the spaces are reserved.
The ratio of reserved spaces: not reserved spaces = 1:10.
Work out the number of spaces that are not reserved.
Answers
Step-by-step explanation:
work he in a department store
A consumer group has determined that the distribution of life spans for gas ranges (stoves) has a mean of 15.0 years and a standard deviation of 4.2 years. The distribution of life spans for electric ranges has a mean of 13.4 years and a standard deviation of 3.7 years. Both distributions are moderately skewed to the right. Suppose we take a simple random sample of 35 gas ranges and a second SRS of 40 electric ranges. Which of the following best describes the sampling distribution of the difference in mean life span of gas ranges and electric ranges?
a. Mean = 1.6 years, standard deviation = 7.9 years, shape: moderately right-skewed.
b. Mean = 1.6 years, standard deviation - 0.92 years, shape: approximately Normal.
c. Mean= 1.6 years, standard deviation = 0.92 years, shape: moderately right skewed.
d. Mean =1.6 years, standard deviation =0.40 years, shape: approximately Normal.
e. Mean =1.6 years, standard deviation =0.40 years, shape: moderately right skewed.
Answers
Answer:
b. Mean = 1.6 years, standard deviation - 0.92 years, shape: approximately Normal.
Step-by-step explanation:
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Subtraction of normal Variables:
When we subtract normal variables, the mean is the subtraction of the means, while the standard deviation is the square root of the sum of the variances.
A consumer group has determined that the distribution of life spans for gas ranges (stoves) has a mean of 15.0 years and a standard deviation of 4.2 years. Sample of 35:
This means that:
\(\mu_G = 15\)
\(s_G = \frac{4.2}{\sqrt{35}} = 0.71\)
The distribution of life spans for electric ranges has a mean of 13.4 years and a standard deviation of 3.7 years. Sample of 40:
This means that:
\(\mu_E = 13.4\)
\(s_E = \frac{3.7}{\sqrt{40}} = 0.585\)
Which of the following best describes the sampling distribution of the difference in mean life span of gas ranges and electric ranges?
Shape is approximately normal.
Mean:
\(\mu = \mu_G - \mu_E = 15 - 13.4 = 1.6\)
Standard deviation:
\(s = \sqrt{s_G^2+s_E^2} = \sqrt{0.71^2+0.585^2} = 0.92\)
So the correct answer is given by option b.
Constructed line PQ is the _______________ of line segment CD.

Answers
Answer:
Perpendicular bisector
Step-by-step explanation:
Construction done:
1). An arc is drawn from point O which intersects line 'l' at two points C and D.
2). From the points C and D two equal arcs on both the sides of the line 'l' have been drawn intersecting each other at points P and Q.
3). Points P and Q have been joined with the help of a straightedge.
Hence constructed line PQ is the PERPENDICULAR BISECTOR of the line segment CD.
Based on the values in the table below, find the slope and y-intercept to write the equation of the line in the form y=mx+b.
x= 1, 2, 3
y= 11, 22, 33
Answers
Answer:
y= 11x
Step-by-step explanation:
find the slope: 22-11/2-1= 11/1 or 11
To find the y-intercept you can use the slope by subtracting 11 (inverse operation) from the y value of (1,11). So the y- intercept is (0,0). To write the equation plug in 11 for m and 0 for b. Since 0 has no value the equation would be y= 11x
Quick does anyone know this please give me the right answer ( this is due in 20 minutes)

Answers
Answer:
32?
Step-by-step explanation:
Answer: I believe it is 670 sq. ft.
Step-by-step explanation:
Someone correct me if I'm wrong. I feel as though this is wrong.
Can anyone help me?pls

Answers
Answer:
b = 8.89, c = 11.96 and m∠B = 48°
Step-by-step explanation:
From the given triangle ABC,
We will apply sine ratio for angle A,
sin(A) = \(\frac{\text{Opposite side}}{\text{Hypotenuse}}\)
sin(42)° = \(\frac{BC}{AB}\)
sin(42)° = \(\frac{8}{AB}\)
AB = \(\frac{8}{\text{sin}(42)}\)
AB = 11.96
c = 11.96
By triangle sum theorem,
m∠A + m∠B + m∠C = 180°
42° + m∠B + 90° = 180°
m∠B = 180 - 132
m∠B = 48°
By cosine ratio of angle A,
cos(A) = \(\frac{\text{Adjacent side}}{\text{Hypotenuse}}\)
cos(42)° = \(\frac{AC}{AB}\)
AC = AB.cos(42)°
AC = (11.96)cos(42)°
AC = 8.89
b = 8.89
1. Allison is buying a home. It cost her $230,000. She has to put a down payment of 10% of the purchase price. How much is her down
payment?
$13,000
$23,000
$30,000
$2,000
Answers
The following selected information was extracted from the records of B Solomon.
1. B Solomon, the owner of Solomon Traders, bought a new Machine for R250 000 on 1 July 2013.
2. On 1 October 2014, he purchased a second Machine for R350 000 cash.
3. On 30 June 2015, the Machine bought during 2013 was sold for R120 000 cash.
4. It is the business’ policy to depreciate Machines at 20% per annum on cost.
REQUIRED:
Prepare the following ledger accounts reflecting all applicable entries, in the books of Solomon Traders, properly balanced/closed off, for the years ended 31 March 2016:
1.1. Accumulated depreciation.
1.2. A Machines realisation.
NB: Show all calculations as marks will be awarded for calculations.
Answers
1.1. Accumulated depreciation:
The accumulated depreciation for the machine bought on 1 July 2013 would be R150,000 as of 31 March 2016.
1.2. Machine realization:
The machine bought in 2013 was sold for R120,000 on 30 June 2015, resulting in a profit/loss on the sale of R10,000.
1.1. Accumulated Depreciation:
To calculate the accumulated depreciation, we need to determine the annual depreciation expense for each machine and then accumulate it over the years.
Machine bought on 1 July 2013:
Cost: R250,000
Depreciation rate: 20% per annum on cost
Depreciation expense for the year ended 31 March 2014: 20% of R250,000 = R50,000
Depreciation expense for the year ended 31 March 2015: 20% of R250,000 = R50,000
Depreciation expense for the year ended 31 March 2016: 20% of R250,000 = R50,000
Accumulated depreciation for the machine bought on 1 July 2013:
As of 31 March 2014: R50,000
As of 31 March 2015: R100,000
As of 31 March 2016: R150,000
1.2. Machine Realisation:
To record the sale of the machine bought in 2013, we need to adjust the machine's value and the accumulated depreciation.
Machine's original cost: R250,000
Accumulated depreciation as of 30 June 2015: R100,000
Net book value as of 30 June 2015:
R250,000 - R100,000 = R150,000.
On 30 June 2015, the machine was sold for R120,000.
Realisation amount: R120,000
To record the sale:
Debit Cash: R120,000
Debit Accumulated Depreciation: R100,000
Credit Machine: R250,000
Credit Machine Realisation: R120,000
Credit Profit/Loss on Sale of Machine: R10,000 (difference between net book value and realisation amount).
These entries will reflect the appropriate balances in the ledger accounts and properly close off the accounts for the years ended 31 March 2016.
For similar question on depreciation.
https://brainly.com/question/15998639
#SPJ8
If ABCD is dilated by a factor of 3, the
coordinate of B' would be:
-5 -4
MA
А
B
3
26
1
-2 -10
-1
-2.
-3
C
2 3 4 5
D
B' = ([?], [])
Enter
Answers
If ABCD is dilated by a scale factor of 3, the coordinate of B' would be (-6, 6).
What is dilation?In Geometry, dilation simply refers to a type of transformation which typically changes the size of a geometric object, but not its shape.
This ultimately implies that, the size of the geometric shape would be increased (stretched or enlarged) or decreased (compressed or reduced) based on the scale factor applied.
Next, we would apply a dilation to the coordinates of the pre-image by using a scale factor of 3 centered at the origin as follows:
Ordered pair B (-2, 2) → Ordered pair B' (-2 × 3, 2 × 3) = Ordered pair B' (-6, 6).
Read more on scale factor here: brainly.com/question/20482938
#SPJ1
3
2
Show gred
1
16
-5
4
1 2
3
4
5 6
3 -2 -1
11
-5
-6
- x2. on
sin - cos - tan-
+ - X + / +
log-e? 10
-
10n
Show less

Answers
Answer:
The gradient of the graph below is \(\mathbf{\frac{3}{2} }\)
Step-by-step explanation:
We need to calculate the gradient of the graph
The gradient of graph is actually slope of the graph.
The slope of graph can be calculated using formula: \(Slope=\frac{y_2-y_1}{x_2-x_1}\)
Taking any 2 points on graph i.e
(1,0) and (-1,-3)
We have \(x_1=1, y_1=0, x_2=-1,y_2=-3\)
Putting values and finding gradient:
\(Slope=\frac{y_2-y_1}{x_2-x_1}\\Slope=\frac{-3-0}{-1-1}\\Slope=\frac{-3}{-2}\\Slope=\frac{3}{2}\)
So, The gradient of the graph below is \(\mathbf{\frac{3}{2} }\)
The largest prime number that is a factor of 35 is multiplied by the smallest prime number
Answers
Answer:
the largest factor of 35 is 35 and the smallest prime number is 2 so 35 times two is 70
Step-by-step explanation:
how do you solve the inequality of -11.3 is equal to or greater than -4.7 + 4x
Answers
Answer: -1.65 ≥ x
Step-by-step explanation:
We usually express "equal to or greater than" by using the symbol ≥.
And we set up the inequality by looking at the word description, then we have:
-11.3 ≥ -4.7 + 4x plus 4.7 on both sides.
-6.6 ≥ 4x divide 4 on both sides.
-1.65 ≥ x
The following question has two parts. First answer part A. Then,
answer part B
In math class, Alyssa's average test score is 90.125.
Part A
What is 90.125 written in expanded form?
х
A 9 x 10+1x1+2 x + 5 x
1
100
X B. 9x1+1x D + 2 x
100
+5
1,000
C. 9 x 10+1 x 1 + 2 x 100 + 5 x 1000
х
D. 9x1+1 100 + 2 x 1000 + 5 x
10.000
Answers

center (-4, -7), tangent to x = 2
Answers
Answer:
(x + 4)^2 + (y + 7)^2 = 36
Step-by-step explanation:
The given information describes a circle with its center at (-4, -7) and tangent to the vertical line x = 2. To determine the radius of the circle, we need to find the distance between the center and the tangent line.
The distance between a point (x1, y1) and a line Ax + By + C = 0 is given by:
d = |Ax1 + By1 + C| / sqrt(A^2 + B^2)
In this case, the equation of the line is x = 2, which can be written as 1x + 0y - 2 = 0. Therefore, A = 1, B = 0, and C = -2. The center of the circle is (-4, -7), so x1 = -4 and y1 = -7. Substituting these values into the formula, we get:
d = |1*(-4) + 0*(-7) - 2| / sqrt(1^2 + 0^2)
d = |-6| / sqrt(1)
d = 6
Therefore, the radius of the circle is 6 units. The equation of a circle with center (h,k) and radius r is given by:
(x - h)^2 + (y - k)^2 = r^2
Substituting the values we have found, we get:
(x + 4)^2 + (y + 7)^2 = 36
This is the equation of the circle that satisfies the given conditions.
BONJOUR AIDEZ MOI SIL VOUS PLAIT

Answers
The distance from the center of the Earth to the point where the net gravitational force is zero is one-ninth the distance from the Earth to the Moon.
Let's assume that the distance from the center of the Earth to this point is denoted as x.
Given:
Mass of the Moon (M\(_{moon}\)) = 1/81 × M\(_{earth}\)
Distance from Earth to Moon (d\(_{moon}\)) = distance on center
According to the principle of gravitational equilibrium, the gravitational force from the Earth and the gravitational force from the Moon acting on an object at that point must balance out. Mathematically, we can express this as:
F\(_{earth}\) = F\(_{moon}\)
The gravitational force between two objects can be calculated using Newton's law of universal gravitation:
F \(_{gravity}\)= G × (m₁ × m₂) / r²
Where:
G is the gravitational constant (approximately 6.67430 x 10⁻¹¹m²/kg/s²)
m₁ and m₂ are the masses of the two objects
r is the distance between the centers of the two objects
Considering the gravitational forces involved:
F\(_{gravity}\)\(_{earth}\) = G ₓ (M\(_{EARTH}\) ₓ m\(_{OBJECT}\)) / (d\(_{earth}\))²
F\(_{gravity}\) \(_{moon}\) = G ₓ (M \(_{moon}\) ₓ m\(_{object}\)) / (d \(_{moon}\))²
Since we are looking for the point where the net gravitational force is zero, we set these two forces equal to each other:
G × (M\(_{earth}\) × m\(_{object}\)) / (d\(_{earth}\))² = G × (M \(_{moon}\) × m\(_{object}\)) / (d \(_{moon}\))²
Canceling out the common factors of G and m\(_object}\), and substituting the given values:
(M\(_{earth}\) × 1) / (d\(_{earth}\))² = (M \(_{moon}\) × 1) / (d \(_{moon}\))²
Rearranging the equation:
(d\(_{earth}\))²/ (M\(_{earth}\)) = (d \(_{moon}\))² / (M \(_{moon}\))
Taking the square root of both sides:
d\(_{earth}\) / √(M \(_{moon}\))) = d_moon / √(M \(_{moon}\))
Substituting the given values:
d\(_{earth}\) /√(M\(_{earth}\)) = d\(_{moon}\) / √(1/81 × M\(_{earth}\))
Simplifying further:
d\(_{earth}\) / √(M\(_{earth}\)) =d\(_{moon}\) / (1/9 × √(M\(_{earth}\)))
Multiplying both sides by √(M\(_{earth}\)):
d\(_{earth}\) = (1/9) × d\(_{moon}\)
To know more about gravitational force
https://brainly.com/question/27943482
#SPJ4
The population of Country A is about 1,070,000 and the population of
Country B is about 10,459,000. Approximately how many times greater is
the population of Country B than the population of Country A? Write your
answer as a power of 10.
Answers
About 1,070,000 people live in Country A, while 10,459,000 people live in Country B. The population of Country B is roughly 9389×10³ times larger than that of Country A.
Given that,
About 1,070,000 people live in Country A, while 10,459,000 people live in Country B.
We have to find the population of Country B is roughly how many times larger than that of Country A.
We have to subtract the population of Country B to Country A.
=10,459,000-1,070,000
=9389000
=9389×10³
Therefore, the population of Country B is roughly 9389×10³ times larger than that of Country A.
To learn more about larger visit: https://brainly.com/question/25009162
#SPJ1
What is the area of the square that measures 3.1 m on each side
Answers
The area of the square with a side length of 3.1 meters is 9.61 square meters.
To find the area of a square, we need to multiply the length of one side by itself. In this case, the square has a side length of 3.1 m.
Area of a square = side length × side length
Substituting the given side length into the formula:
Area = 3.1 m × 3.1 m
To perform the calculation:
Area = 9.61 m²
It's worth noting that when calculating the area, we are working with squared units. In this case, the side length is in meters, so the area is expressed in square meters (m²). The area represents the amount of space enclosed within the square.
Remember, to find the area of any square, you simply need to multiply the length of one side by itself.
The area of the square with a side length of 3.1 meters is 9.61 square meters.
For more such questions on square
https://brainly.com/question/27307830
#SPJ8
In the figure points A B C D and E are collinear. If AE = 38 and BD = 15
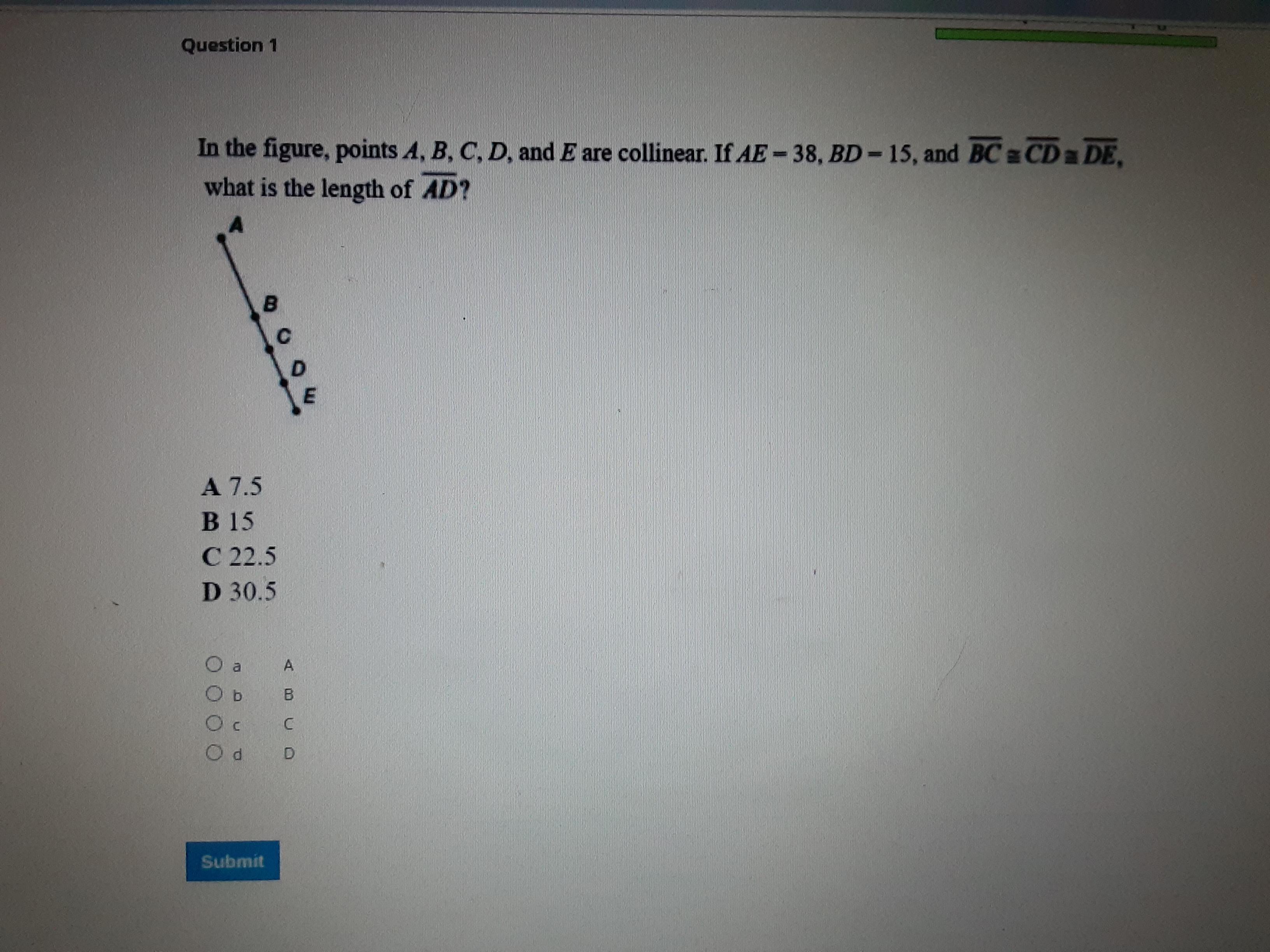
Answers
Answer:
D. 30.5
Step-by-step explanation:
Given that A, B, C, D, and E are collinear,
AE = 38,
BD = 15, since segment BC = CD = DE, therefore
BD = ⅔ of BE
15 = ⅔*BE (substitution)
Solve for BE
Multiply each side by 3
15*3 = ⅔*BE*3
45 = 2*BE
Divide both sides by 2
45/2 = BE
22.5 = BE
BE = 22.5
Find AB:
AB + BE = AE (segment addition postulate)
AB + 22.5 = 38 (Substitution)
AB = 38 - 22.5 (Subtracting 22.5 from each side)
AB = 15.5
Find length of segment AD:
AB + BD = AD (segment addition postulate)
15.5 + 15 = AD (Substitution)
30.5 = AD
AD = 30.5