NEED THIS DONE ASAP!! Thank you!!
Given a circle with are 225pi cm^2.
What is the length of an arc with a central angle of 30°? Show your work.

Answers
\( \sf{\qquad\qquad\huge\underline{{\sf Answer}}} \)
Here we go ~
Area of circle is :
\(\qquad \sf \dashrightarrow \: a = 225\pi \: \: cm {}^{2} \)
\(\qquad \sf \dashrightarrow \: \pi{r}^{2} = 225 \pi\)
\(\qquad \sf \dashrightarrow \: {r}^{2} = 225\)
\(\qquad \sf \dashrightarrow \:r = \sqrt{225} \)
\(\qquad \sf \dashrightarrow \:r = 15\)
Now, let's find the arc of circle which makes an angle 30° at centre.
\(\qquad \sf \dashrightarrow \: \dfrac{ \theta}{360} (2 \pi r)\)
\(\qquad \sf \dashrightarrow \: \dfrac{30}{360} (2 \sdot\pi \sdot15)\)
\(\qquad \sf \dashrightarrow \: \dfrac{30 \pi}{12} \)
\(\qquad \sf \dashrightarrow \:5/2 \pi\)
So, the length of required arc is 2.5 pi or 7.85 cm
Answer:
7.85 cm (2 d.p.)
Step-by-step explanation:
Step 1: Find the radius
\(\textsf{Area of a circle}=\pi r^2 \quad \textsf{(where r is the radius)}\)
Given:
Area = 225π cm²Substitute the given value into the formula and solve for r:
\(\implies 225 \pi= \pi r^2\)
\(\implies r^2=225\)
\(\implies r=\sqrt{225}\)
\(\implies r=15 \:\: \sf cm\)
Step 2: Find the arc length
\(\textsf{Arc length}=2 \pi r\left(\dfrac{\theta}{360^{\circ}}\right) \quad \textsf{(where r is the radius and}\:\theta\:{\textsf{is the angle in degrees)}\)
Given:
\(\theta\) = 30°r = 15 cm (from step 1)Substitute the given values into the formula and solve for arc length:
\(\implies \textsf{Arc length}=2 \pi (15) \left(\dfrac{30^{\circ}}{360^{\circ}}\right)\)
\(\implies \textsf{Arc length}=\dfrac{5}{2}\pi \:\: \sf cm\)
\(\implies \textsf{Arc length}=7.85 \:\: \sf cm\:\:(2\:d.p.)\)
Related Questions
Fifteen elves made some identical cakes for a
party. Each elf ate half of a cake, one-fifth of a
cake, and a third piece, which was six times
smaller than the second piece. Three cakes
were left untouched. How many cakes did the
elves make?
Answers
To solve this problem, we can use algebra. Let's say the total number of cakes the elves made is "x". Then, each elf ate half of a cake, which means they collectively ate 7.5x cakes. Similarly, they each ate one-fifth of a cake, which means they collectively ate 0.3x cakes. Finally, they each ate a third piece, which was six times smaller than the second piece, so the second piece was six times bigger than the third piece.
Now we can set up an equation:
7.5x + 0.3x + 6(0.3x) + 3 = x
Simplifying and solving for x, we get:
8.1x + 3 = x
7.1x = 3
x ≈ 0.42
However, since we're looking for a whole number of cakes, we know that the elves made either 0 or 1 cakes. Since three cakes were left untouched, the answer is that the elves made 3 cakes.
To learn more about whole number click here : brainly.com/question/29766862
#SPJ11
To solve this problem, we can use algebra. Let's say the total number of cakes the elves made is "x". Then, each elf ate half of a cake, which means they collectively ate 7.5x cakes. Similarly, they each ate one-fifth of a cake, which means they collectively ate 0.3x cakes. Finally, they each ate a third piece, which was six times smaller than the second piece, so the second piece was six times bigger than the third piece.
Now we can set up an equation:
7.5x + 0.3x + 6(0.3x) + 3 = x
Simplifying and solving for x, we get:
8.1x + 3 = x
7.1x = 3
x ≈ 0.42
However, since we're looking for a whole number of cakes, we know that the elves made either 0 or 1 cakes. Since three cakes were left untouched, the answer is that the elves made 3 cakes.
To learn more about whole number click here : brainly.com/question/29766862
#SPJ11
Name the angle that corresponds to angle 2.

Answers
Answer:
c) angle 4
Step-by-step explanation:
correspond is same spot but diagonally.
A small hotel in central London has 8 rooms. Based on data collected over the last five years, it was estimated that the probability a room is occupied on any particular "weekend" night (Saturday and Sunday) is 0.75. This is the probability of success. On any particular "weekend" night, a hotel is only occupied (Success) or not occupied (Failure). There are no other possibilities. Required: What is the probability that at least 4 of the 7 hotel rooms are occupied on any weekend night? Note: Show all your calculations in well laid-out Excel spreadsheet tables with clear headings and include formulas. Give your answers correct to 3 decimal places.
Answers
Based on the given data, the probability of a room being occupied on any particular weekend night is 0.75. To calculate the probability that at least 4 out of the 7 rooms are occupied on a weekend night, we can use the binomial probability formula. By summing up the probabilities for 4, 5, 6, and 7 occupied rooms, we find that the probability is approximately 0.923.
To calculate the probability, we can use the binomial probability formula, which states that the probability of getting exactly k successes in n independent Bernoulli trials, each with a probability p of success, is given by the formula:
P(X = k) = (n choose k) * p^k * (1 - p)^(n - k)
In this case, we want to find the probability of at least 4 out of 7 rooms being occupied on a weekend night. We can calculate this by summing up the probabilities of getting 4, 5, 6, and 7 occupied rooms.
For 4 occupied rooms:
P(X = 4) = (7 choose 4) * 0.75^4 * (1 - 0.75)^(7 - 4) = 0.339
For 5 occupied rooms:
P(X = 5) = (7 choose 5) * 0.75^5 * (1 - 0.75)^(7 - 5) = 0.395
For 6 occupied rooms:
P(X = 6) = (7 choose 6) * 0.75^6 * (1 - 0.75)^(7 - 6) = 0.266
For 7 occupied rooms:
P(X = 7) = (7 choose 7) * 0.75^7 * (1 - 0.75)^(7 - 7) = 0.122
To find the probability of at least 4 occupied rooms, we sum up the probabilities for 4, 5, 6, and 7 occupied rooms:
P(X >= 4) = P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7) = 0.339 + 0.395 + 0.266 + 0.122 = 0.923
Therefore, the probability that at least 4 out of the 7 hotel rooms are occupied on any weekend night is approximately 0.923, or 92.3% when rounded to three decimal places.
Learn more about probability here: brainly.com/question/32117953
#SPJ11
Based on the given data, the probability of a room being occupied on any particular weekend night is 0.75.
To calculate the probability that at least 4 out of the 7 rooms are occupied on a weekend night, we can use the binomial probability formula. By summing up the probabilities for 4, 5, 6, and 7 occupied rooms, we find that the probability is approximately 0.923.
To calculate the probability, we can use the binomial probability formula, which states that the probability of getting exactly k successes in n independent Bernoulli trials, each with a probability p of success, is given by the formula:
P(X = k) = (n choose k) * p^k * (1 - p)^(n - k)
In this case, we want to find the probability of at least 4 out of 7 rooms being occupied on a weekend night. We can calculate this by summing up the probabilities of getting 4, 5, 6, and 7 occupied rooms. For 4 occupied rooms:
P(X = 4) = (7 choose 4) * 0.75^4 * (1 - 0.75)^(7 - 4) = 0.339
For 5 occupied rooms:
P(X = 5) = (7 choose 5) * 0.75^5 * (1 - 0.75)^(7 - 5) = 0.395
For 6 occupied rooms:
P(X = 6) = (7 choose 6) * 0.75^6 * (1 - 0.75)^(7 - 6) = 0.266
For 7 occupied rooms:
P(X = 7) = (7 choose 7) * 0.75^7 * (1 - 0.75)^(7 - 7) = 0.122
To find the probability of at least 4 occupied rooms, we sum up the probabilities for 4, 5, 6, and 7 occupied rooms:
P(X >= 4) = P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7) = 0.339 + 0.395 + 0.266 + 0.122 = 0.923. Therefore, the probability that at least 4 out of the 7 hotel rooms are occupied on any weekend night is approximately 0.923, or 92.3% when rounded to three decimal places.
Learn more about probability here: brainly.com/question/32117953
#SPJ11
5. HELP FAST If each person paid an equal amount, who would save the most money? Explain your reasoning using at least two complete sentences
Answers
Person A would save the most money because they had a coupon that was worth more than their portion of the purchase price.
To determine who would save the most money if each person paid an equal amount, we need to calculate how much each person paid and then compare the amounts saved by each person. For instance, let's consider an example with four people who want to split the cost of a $60 purchase equally. Each person would pay $60 / 4 = $15.
If person A has a $20 coupon, then they would save $20, and their net cost would be $15 - $20 = -$5. Person B has a $15 coupon, so they would save $15, and their net cost would be $15 - $15 = $0. Person C has a $10 coupon, so they would save $10, and their net cost would be $15 - $10 = $5. Person D has a $5 coupon, so they would save $5, and their net cost would be $15 - $5 = $10.
You can learn more about coupons at: brainly.com/question/31727353
#SPJ11
Could. you write this down on a paper and make graphs
The vertex of the parabola is (0, 36), so the equation of the parabola will be of the form y = a(x - 0)^2 + 36, where a is a negative number.
We know that the parabola crosses the x-axis at (-6, 0) and (6, 0), so we can substitute these points into the equation to get two equations:
0 = a(-6 - 0)^2 + 36
0 = a(6 - 0)^2 + 36
Solving these equations, we get a = -1.
Therefore, the equation of the rainbow parabola is y = -(x^2) + 36.
Table of values for the linear function
The drone intersects the parabola at (-4, 20) and (4, 20), so the linear function must pass through these points.
Let's call the linear function f(x). We can then write two equations to represent the two points of intersection:
f(-4) = 20
f(4) = 20
Solving these equations, we get f(x) = 20.
A table of values for f(x) is shown below:
x | f(x)
---|---
-4 | 20
-3 | 18
-2 | 16
-1 | 14
0 | 12
1 | 10
2 | 8
3 | 6
4 | 4
Answers
Tip:
I don't wish to make the graph but here is some advice,
Parabola:
The equation of the parabola is y = -(x^2) + 36. The vertex of the parabola is at (0, 36), and it opens downward. The parabola crosses the x-axis at (-6, 0) and (6, 0).
Linear Function:
The linear function is represented by f(x) = 20. It is a horizontal line passing through the points (-4, 20) and (4, 20).
Please note that the parabola and linear function intersect at the points (-4, 20) and (4, 20). The linear function remains constant at y = 20 for all other x-values.
Hey help me with some math by zoom. free tutoring yeah?
Answers
Answer:
why can't you write the questions on brainly?
what’s is the distance between (-2,7) and (-5,9)
Answers
We can use the distance formula to find the distance between two points in a coordinate plane:
d = √[(x2 - x1)² + (y2 - y1)²]
where (x1, y1) and (x2, y2) are the coordinates of the two points, and d is the distance between them.
Using the given coordinates of the two points, we have:
x1 = -2, y1 = 7
x2 = -5, y2 = 9
Substituting these values into the distance formula, we get:
d = √[(-5 - (-2))² + (9 - 7)²]
d = √[(-3)² + 2²]
d = √(9 + 4)
d = √13
Therefore, the distance between the points (-2, 7) and (-5, 9) is approximately √13 units. We can also approximate this value as 3.61 units (rounded to two decimal places).
Solve the inequality 4y + 7< 16
Answers
Answer:
y = 28
Step-by-step explanation:
At James Middle School, there are 480 students enrolled in
algebra. The chart shows the grade distribution for one algebra class.

Answers
128
Explanation:
When you add that class together, you get 30. You then divide 480/30 giving you 16. You then multiply 16*8 since only 8 students got A’s giving you the product of 128!
Hope this helps!!
One month before the election, a poll of 630 randomly selected voters showed 54% planning to vote for a certain candidate. A week later, it became known that he had tweeted inappropriate pictures of himself, and a new poll showed only 51 % of 1010 voters supporting him. Do these results indicate a decrease in voter support for his candidacy? Test an appropriate hypothesis and state your conclusion
Answers
To determine whether there is a decrease in voter support for the candidate after the scandal, we can test the hypothesis using the proportions of the two polls. The first poll showed 54% support among 630 randomly selected voters, while the second poll showed 51% support among 1010 voters. By conducting a hypothesis test, we can determine if the difference in proportions is statistically significant.
To test the hypothesis, we can use the two-sample z-test for proportions. The null hypothesis (H0) assumes no difference in voter support, while the alternative hypothesis (H1) assumes a decrease in support. We can calculate the test statistic using the formula:
z = (p1 - p2) / √[(p(1 - p) / n1) + (p(1 - p) / n2)]
where p1 and p2 are the proportions from the two samples, and n1 and n2 are the respective sample sizes. p is the pooled proportion, calculated as (x1 + x2) / (n1 + n2), where x1 and x2 are the respective number of successes (votes for the candidate) in each sample.
By calculating the z-value, we can compare it to the critical value for the desired significance level (e.g., α = 0.05). If the z-value exceeds the critical value, we reject the null hypothesis in favor of the alternative hypothesis, indicating a statistically significant decrease in voter support.
After performing the calculations, if the z-value exceeds the critical value, we can conclude that there is evidence to support the claim of a decrease in voter support for the candidate after the scandal. Conversely, if the z-value does not exceed the critical value, we fail to reject the null hypothesis, suggesting that there is insufficient evidence to conclude a significant decrease in support.
To learn more about z-test click here : brainly.com/question/30109604
#SPJ11
At the instant shown, the shaft and plate rotates with an angular velocity of 19 rad/s and angular acceleration of 9 rad/s2 0.6 m 0.2 m 0.4m 0.3 m 0.3 m 0.4 m Part A eterminethe wocl a n D sea c Enter the ", y, and Z components of the velocity separated by commas vec m/s Submit Request Answer Part B Determine the acceleration of point D located on the corner of the plate at this instant. Enter the , y, and Z components of the velocity separated by commas vec m/s Submit Request Answer
Answers
The acceleration components of point D are, ax = 3.6 m/s², ay = 6.4 m/s², az = -1.14 m/s²
At the instant shown, the shaft and plate rotates with an angular velocity of 19 rad/s and angular acceleration of 9 rad/s2. The given diagram is shown below. Angular velocity (w) = 19 rad/sAngular acceleration (α) = 9 rad/s²Plate dimension AB = 0.6 m, BC = 0.2 m, CD = 0.4 m, DA = 0.3 m, AE = 0.3 m and EF = 0.4 m.
Determine the wocl and Dsea of Enter the ", y, and Z components of the velocity separated by commas vec m/sThe velocity components for point D can be calculated using the following formula.Vd = R x wWhere R is the position vector of D relative to the origin.
According to the given diagram, the position vector of point D relative to the origin is, R = 0.2i + 0.4j + 0.3kThe velocity of point D can be calculated as follows.Vd = R x w = 0.2i + 0.4j + 0.3k x 19The cross product of R and w can be calculated as follows.i j k 0.2 0.4 0.3 0 19 0 = [(0.4 × 0) - (0.3 × 19)] i - [(0.2 × 0) - (0.3 × 0)] j + [(0.2 × 19) - (0.4 × 0)] kVd = -5.7i + 6.8kThus, the velocity components of point D are, Vx = -5.7 m/s, Vy = 0 m/s, Vz = 6.8 m/s
Determine the acceleration of point D located on the corner of the plate at this instant. Enter the, y, and Z components of the velocity separated by commas vec m/sThe acceleration components of point D can be calculated using the following formula.aD = R x α + w x (w x R)Where R is the position vector of D relative to the origin.
According to the given diagram, the position vector of point D relative to the origin is, R = 0.2i + 0.4j + 0.3kThe acceleration of point D can be calculated as follows.aD = R x α + w x (w x R) = (0.2i + 0.4j + 0.3k) x 9 + 19 x (19 x (0.2i + 0.4j + 0.3k)) = (0.4k - 0.3j) x 9 + 19 x (0.4 x (0.4j - 0.3k))aD = 3.6i + 6.4j - 1.14k.
Learn more about Acceleration
brainly.com/question/12550364
#SPJ11
Hello! Help please 5 questions for 17 points
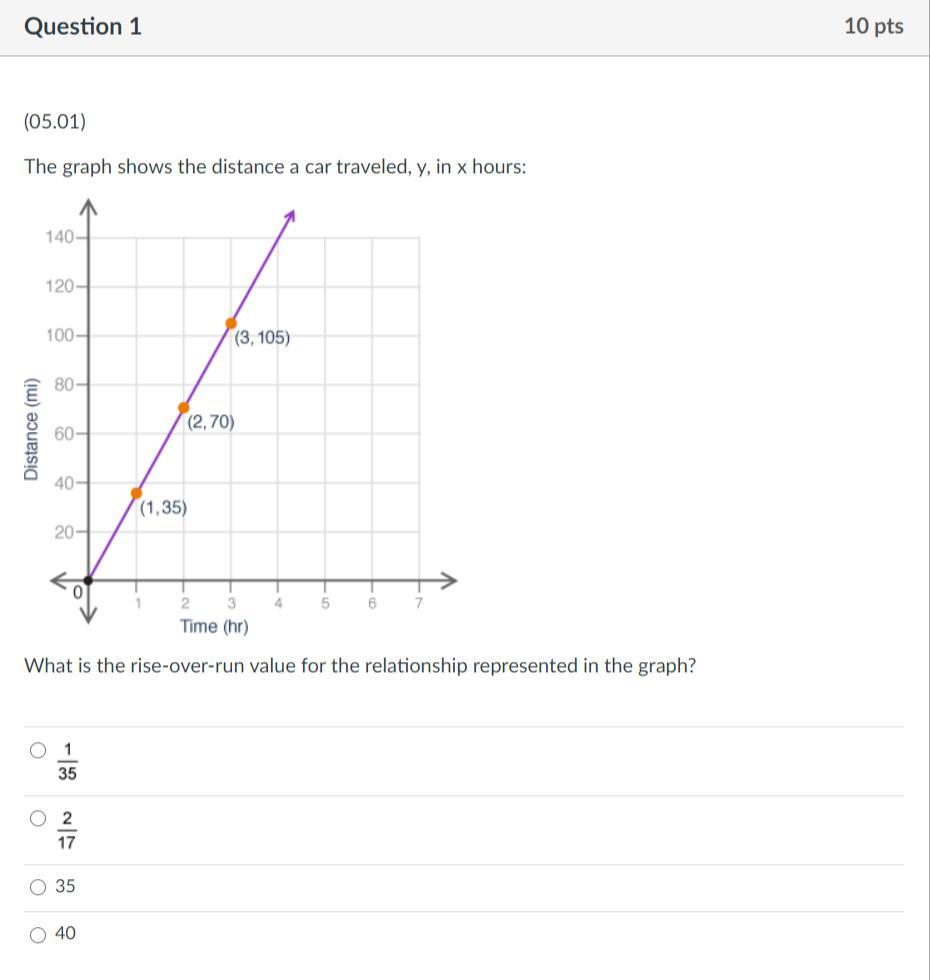



Answers
1. 1/35 it goes up 35 and goes right 1
What is the weight of a 24 square foot 2 inch thick aluminum plate with a unit weight of 15 lbs?
Answers
Weight of a 24 square foot, 2 inch thick aluminum plate will be: 720 lbs.
What is unitary method?A single unit's value can be determined from the values of multiple units, and multiple units' values can be determined from the values of single units using the unitary method.
Given:
Weight of 1 square foot, 1 inch thick plate = 15 lbs.To find: weight of a 24 square foot, 2 inch thick aluminum plate
Finding:
By unitary method, we get:
Weight of 1 square foot aluminum plate = 15 lbs.
Weight of 24 square foot aluminum plate = 15(24) lbs = 360 lbs.
Again, by unitary method, we get:
Weight of 1 square foot, 1 inch thick aluminum plate = 15 lbs.
Weight of 24 square foot, 1 inch thick aluminum plate = 15(24) lbs = 360 lbs.
Weight of 24 square foot, 2 inch thick aluminum plate = 360(2) lbs = 720 lbs.
Hence, Weight of 24 square foot, 2 inch thick aluminum plate = 720 lbs.
To learn more about unitary method, refer to the link: https://brainly.com/question/24587372
#SPJ4
David is making rice for his guests based on a recipe that requires rice, water, and a special blend of spice, where the rice-to-spice ratio is
15
:
1
15:115, colon, 1. He currently has
40
4040 grams of the spice blend, and he can go buy more if necessary. He wants to make
10
1010 servings, where each serving has
75
7575 grams of rice. Overall, David spends
4.50
4.504, point, 50 dollars on rice.
What is the price of rice per gram?
Answers
Answer:
The price of rice per gram is 4.50 / 750 = 0.006 dollars per gram.
Step-by-step explanation:
David wants to make 10 servings, where each serving has 75 grams of rice. So, he needs a total of 10 * 75 = 750 grams of rice. the price of rice per gram is 4.50 / 750 = 0.006 dollars per gram.
find the area of the region inside the circle r=4cosθ and to the right of the vertical line r=secθ.
Answers
The area of the region inside the circle r = 4cos(θ) and to the right of the vertical line r = sec(θ) is \(2\pi - 2\cos^{-1}\left(\frac{1}{4}\right) - \sqrt{15}\).
To find the area of the region inside the circle r = 4cos(θ) and to the right of the vertical line r = sec(θ), we need to determine the limits of integration for θ.
First, let's find the values of θ where the circle and the vertical line intersect:
r = 4cos(θ)
sec(θ) = 4cos(θ)
To simplify the equation, let's convert sec(θ) to its reciprocal form:
1/cos(θ) = 4cos(θ)
Multiplying both sides by cos(θ), we get:
1 = 4\(cos^2\)(θ)
Rearranging the equation, we have:
4\(cos^2\)(θ) - 1 = 0
Using the identity \(cos^2\)(θ) - \(sin^2\)(θ) = 1, we can rewrite the equation as:
\(cos^2\)(θ) - \(sin^2\)(θ) = 1/4
Applying the double-angle formula for cosine, we get:
cos(2θ) = 1/4
Taking the inverse cosine of both sides, we have:
2θ = ± \(\cos^{-1}\left(\frac{1}{4}\right)\)
Solving for θ, we get two values:
θ = ± (1/2) \(\cos^{-1}\left(\frac{1}{4}\right)\)
Since we are interested in the region to the right of the vertical line, we'll consider the positive value of θ:
θ = (1/2) \(\cos^{-1}\left(\frac{1}{4}\right)\)
Now, we can find the area by evaluating the integral:
A = ∫[θ, π/2] 1/2 (\(r^2\)) dθ
Substituting the equations for r, we have:
\(A = \int_{\theta}^{\frac{\pi}{2}} \frac{1}{2} (4\cos^2(\theta)) \, d\theta\)
Simplifying further:
\(A = \int_{\theta}^{\frac{\pi}{2}} 8\cos^2(\theta) \, d\theta\)
Using the double-angle formula for cosine, we have:
A = ∫[θ, π/2] 4(1 + cos(2θ)) dθ
Integrating term by term, we get:
A = [4θ + 2sin(2θ)] evaluated from θ to π/2
Now, Substituting the limits of integration, we get:
A = [4(π/2) + 2sin(2(π/2))] - [4θ + 2sin(2θ)] evaluated from θ to π/2
Simplifying:
A = 2π + 2sin(π) - (4θ + 2sin(2θ))
Since sin(π) = 0, we can simplify further:
A = 2π - (4θ + 2sin(2θ))
Now, we need to substitute the value of θ, which we found earlier:
θ = (1/2) \(\cos^{-1}\left(\frac{1}{4}\right)\)
Substituting this value, we have:
A = 2π - (4(1/2) \(\cos^{-1}\left(\frac{1}{4}\right)\) + 2sin(2(1/2) \(\cos^{-1}\left(\frac{1}{4}\right)\)))
Simplifying:
A = 2π - (2 \(\cos^{-1}\left(\frac{1}{4}\right)\) + 2sin(\(\cos^{-1}\left(\frac{1}{4}\right)\)))
Since cos(\(\cos^{-1}\left(x\right)\)) = x, we have:
A = 2π - (2 \(\cos^{-1}\left(\frac{1}{4}\right)\) + 2(√(1 - (1/4)^2)))
Simplifying further:
A = 2π - (2 \(\cos^{-1}\left(\frac{1}{4}\right)\) + 2(√(15/16)))
A = 2π - 2 \(\cos^{-1}\left(\frac{1}{4}\right)\) - √15
So, the area of the region inside the circle r = 4cos(θ) and to the right of the vertical line r = sec(θ) is \(2\pi - 2\cos^{-1}\left(\frac{1}{4}\right) - \sqrt{15}\).
Learn more about double-angle formula for cosine here:
https://brainly.com/question/30410697
#SPJ11
It costs Jesse $1600 to maintain and drive his car for 32 000 km.
find the cost in $ per km.
Answers
Answer:
$20
Step-by-step explanation:
32000 divided by 1600 is 20
so the answer will be $20.
thank you, and if this is right, please let me know!
Answer:
$0.05 per km.
Step-by-step explanation:
1600/32000
= 16/320
= 1/20
= $0.05.
HELP HELP HELP HELP HELP!
Distribute the following expression, and type the equivalent expression into the text box.
3(12x-6)
Answers
Answer: thanks for brainly points kid
Step-by-step explanation:
Probability Distributions for Discrete Random Variables
Which of the following are discrete random variables?
Select all that apply
1-The number of CDs that a college student owns
2- The number of dogs you own
3- The amount of gas in your car
4- Number of 6s you get when you throw 5 number cubes
5- The number of dog sleds that a competitor uses in an annual sled dog race

Answers
The discrete random variables from the given options are: 1, 2, 4, and 5.
The number of CDs that a college student owns: This is a discrete random variable because the number of CDs can only be a whole number. You cannot have a fractional or continuous value for the number of CDs.
The number of dogs you own: This is a discrete random variable because you can only own a whole number of dogs. You cannot own a fractional or continuous number of dogs.
Number of 6s you get when you throw 5 number cubes: This is a discrete random variable because the number of 6s can only be a whole number from 0 to 5. You cannot have a fractional or continuous value for the number of 6s obtained.
The number of dog sleds that a competitor uses in an annual sled dog race: This is a discrete random variable because the number of dog sleds can only be a whole number. You cannot have a fractional or continuous value for the number of dog sleds used.
On the other hand, the following option is not a discrete random variable:
The amount of gas in your car: This is a continuous random variable because the amount of gas can be any non-negative real number. It can have fractional or continuous values, such as 10.5 liters or 20.25 gallons. Option 1,2,3,4 and 5
For more such questions on random variables visit:
https://brainly.com/question/17217746
#SPJ11
Two identical rubber balls are dropped from different heights. Ball 1 is dropped from a height of 16 feet, and ball 2 is dropped from a height of 64 feet. Write and graph a function for the height of each ball. Then use the graphs to tell when each ball will reach the ground.
a.
Ball 1: h1(t) = 16 − t2
Ball 2: h2(t) = 64 − t2
Ball 1 reaches the ground in 4 sec.
Ball 2 reaches the ground in 8 sec
b. Ball 1: h1(t) = −16t2 + 16
Ball 2: h2(t) = −16t2 + 64
Ball 1 reaches the ground in 1 sec.
Ball 2 reaches the ground in 1.5 sec.
c. Ball 1: h1(t) = −16t2 + 16
Ball 2: h2(t) = −16t2 + 64
Ball 1 reaches the ground in 2 sec.
Ball 2 reaches the ground in 3 sec.
d. Ball 1: h1(t) = −16t2 + 16
Ball 2: h2(t) = −16t2 + 64
Ball 1 reaches the ground in 1 sec.
Ball 2 reaches the ground in 2 sec.
Answers
Height of Ball 1: h₁(t) = −16t² + 16, Ball 2: h₂(t) = −16t² + 64. Ball 1 reaches the ground in 2 sec. Ball 2 reaches the ground in 3 sec. The correct answer is option (c)
To understand why this is the correct answer, let's first understand what the given information represents. Two identical rubber balls are dropped from different heights, and we are asked to find their respective height functions. The height function gives the height of the ball at any given time during its descent.
We know that the height function of a ball dropped from a height h₀ is given by h(t) = −16t² + h₀, where t is the time in seconds since the ball was dropped.
Using this formula, we can find the height functions for the two balls:
For the first ball dropped from a height of 16 feet, the height function is h₁(t) = −16t² + 16.
For the second ball dropped from a height of 64 feet, the height function is h₂(t) = −16t² + 64.
Now, we need to determine when each ball will reach the ground. We can do this by setting h(t) = 0 and solving for t. When h(t) = 0, the ball has hit the ground.
For ball 1: 0 = −16t² + 16, which gives t = 2. Therefore, ball 1 reaches the ground in 2 seconds.
For ball 2: 0 = −16t² + 64, which gives t = 3. Therefore, ball 2 reaches the ground in 3 seconds.
Comparing their graphs, we can see that both balls follow the same shape but start at different heights. Ball 2 starts at a higher point on the y-axis (64 ft) and takes longer to hit the ground. Ball 1 starts at a lower point (16 ft) and hits the ground sooner. This is because the greater the initial height, the longer it takes for the ball to reach the ground.
The correct answer is option (c)
To learn more about function click on,
https://brainly.com/question/2960938
#SPJ1

5(x-3) = 2(x+3) solve for x
Answers
Answer:
7
Step-by-step explanation:
5(x - 3) = 2(x + 3) Distribute
5x - 15 = 2x + 6
+ 15 + 15 Switch sides to the liked terms
5x = 2x + 6 + 15
-2x -2x Switch sides to the liked terms
5x - 2x = 6 + 15
3x = 21 Divide
3 3
x = 7
Answer:
x = 7
Step-by-step explanation:
Equation: 5(x-3) = 2(x+3)
Step 1: Simplify the equation.
5 (x − 3) = 2(x + 3)
(5)(x) + (5)(−3) = (2)(x) + (2)(3) Distribute
5x + −15 = 2x + 6
5x − 15 = 2x + 6
Step 2: Subtract 2x.
5x − 15 −2x = 2x + 6 −2x
3x − 15 = 6
Step 3: Add 15.
3x − 15 + 15 = 6 + 15
3x = 21
Step 4: Divide by 3.
\(\frac{3x}{3} = \frac{21}{3}\)
Step 5: Divide 21 by 3.
The answer is x = 7.
what is a congruent polygon
Answers
A congruent polygon refers to two or more polygons that have the same shape and size. There must be an equal number of sides between two polygons for them to be congruent.
Congruent polygons have parallel sides of equal length and parallel angles of similar magnitude. When two polygons are congruent, they can be superimposed on one another using translations, rotations, and reflections without affecting their appearance or dimensions. Concluding about the matching sides, shapes, angles, and other geometric properties of congruent polygons allows us to draw conclusions about them.
Learn more about Congruent polygons here:
https://brainly.com/question/2096633
#SPJ1
Your friend loans you $20,000 for school. In five years he wants
$40,000 back. What is the interest rate he is charging you?
Remember to show your work.
Answers
The interest rate your friend is charging you for the $20,000 loan is 20% per year.
What is the interest rate on the loan?
The simple interest is expressed as;
A = P( 1 + rt )
Where A is accrued amount, P is principal, r is the interest rate and t is time.
Given that;
The Principal P = $20,000
Accrued amount A = $40,000
Elapsed time t = 5 years
Interest rate r =?
Plug these values into the above formula and solve for the interest rate r:
\(A = P( 1 + rt )\\\\r = \frac{1}{t}( \frac{A}{P} -1 ) \\\\r = \frac{1}{5}( \frac{40000}{20000} -1 ) \\\\r = \frac{1}{5}( 2 -1 ) \\\\r = \frac{1}{5}\\\\r = 0.2 \\\\\)
Converting r decimal to R a percentage
Rate R = 0.2 × 100%
Rate r = 20% per year
Therefore, the interest rate is 20% per year.
Learn more about simple interest here: brainly.com/question/25845758
#SPJ1
Which equation best models the data shown in the scatter plot?
In the graph of scatter plot, the range of the x axis is minus four to four by increment of one and the range of the y axis is minus seven to one by increment of one. On the x axis minus four, minus two, two, and four are labeled. On the y axis minus six, minus four, and minus two are labeled. On the graph, there are points at (-0.5, -7), (0, -5), (0.5, -4), (1, -3), (1, -1), and (2, 1).
A. y = x − 3
B. y = x − 5
C. y = 3x − 3
D. y = 3x − 5
Answers
Answer:
The correct option is;
D. y = 3·x - 5
Step-by-step explanation:
From the graph of the scatter plot created with Microsoft Excel, we have that the first and the last point describe a line of best fit, (with trend line equation included) therefore, we have;
The slope = (1 - (-7))/(2 - (-0.5)) = 3.2
Taking the slope of the line of best fit as approximately equal to 3, we have;
3.2 ≈ 3
The equation of the line in point and slope form is therefore;
y - 1 = 3 × (x - 2)
y = 3·x - 6 + 1
∴ y = 3·x - 5
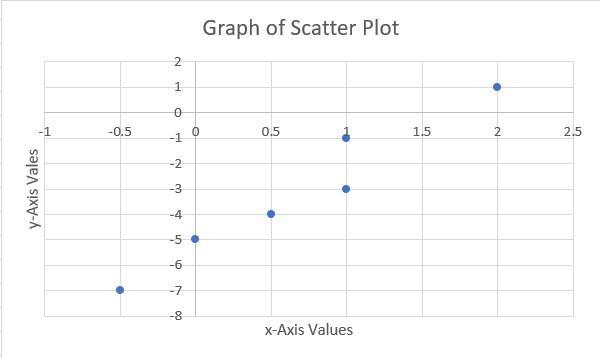

Answer:
D
Step-by-step explanation:
Norman bought 16-pound bag of charcoal for $7.89 and a 10.4-pound bag for 5.69.Whats is the total weight of the two bags of charcoal?
Answers
SOMEONE PLEASE HELP ToT ill make u brain

Answers
Answer:
43
Step-by-step explanation:
18 + 4x - 3
18 + 4(7) - 3
18 + 28 - 3
46 - 3
43
You will plug 7 in the x place since x = 7. Hope this helps, thank you !!
Answer:
18 + 28-3 is 43.
Step-by-step explanation:
4x7 28 that's how I did it
NO LINKSSSSSSSSSSSS please help

Answers
Answer:
I know this aint no clever bro cmon that stuff is easy
Step-by-step explanation:
which best describes the rule for this pattern? 1 comma space minus 12 comma space 12 comma space minus 1, ...
Answers
The rule for the given pattern is to subtract 13, then add 24.
The correct Option is (A.) subtract 13, then add 24.
What is A Number Pattern?A pattern or sequence in a series of numbers is called a number pattern. In general, this pattern builds a connection between all integers.
In this question we have the following pattern:
1, -12, 12, -1
Here we need to find the rule for this pattern.
Let's take the first number of the pattern, which is 1:
1
To obtain the second number of the pattern, which is -12, we must subtract 13, because:
1 - 13 = -12
To obtain the third number of the pattern, which is 12, we must add 24, because:
-12 + 24 = 12
Therefore, the correct answer is A.) subtract 13, then add 24
To know more about number patterns visit:
https://brainly.com/question/29879636
#SPJ4
The complete question is: "Which best describes the rule for this pattern? 1,-12,12,-1 A.) subtract 13, then add 24 B.) subtract -13, then add 24 C.) subtract -24, then add 13 D.) subtract 24, then add 13"
Helen bought fabric for a tablecloth for $8.60 including tax. The sticker price was $7.92.
About what percent sales tax did Helen pay?
9.0%
8.5%
8.0%
7.5%
Answers
Answer:
C.) 8.0%
Step-by-step explanation:
8.60/7.92= 0.68
0.68/8.60=0.079 which rounds up to 0.08
0.08= 8.0%
a parabola opening up or down has vertex (-3,2) and passes through (-7, 2/3) . write its equation in vertex form.
Answers
The equation of the parabola in vertex form is y = (-1/12)(x + 3)^2 + 2, which opens downwards since the leading coefficient is negative.
The equation of the given parabola in vertex form is y = a(x + 3)^2 + 2, where a is a constant that depends on whether the parabola opens up or down.
To determine the value of a, we can use the fact that the parabola passes through (-7, 2/3). Substituting these values into the equation, we get:
2/3 = a(-7 + 3)^2 + 2
2/3 = 16a + 2
16a = -4/3
a = -1/12
Therefore, the equation of the parabola in vertex form is
y = (-1/12)(x + 3)^2 + 2.
The vertex form of a parabola is y = a(x - h)^2 + k, where (h, k) is the vertex of the parabola. In this case, we are given that the vertex is (-3, 2), so we can write the equation as y = a(x + 3)^2 + 2.
To find the value of a, we use the fact that the parabola passes through (-7, 2/3). Substituting these values into the equation, we get 2/3 = a(-7 + 3)^2 + 2. Simplifying this equation, we get 2/3 = 16a + 2, which we can solve for a to get a = -1/12.
Therefore, the final equation of the parabola in vertex form is y = (-1/12)(x + 3)^2 + 2, which opens downwards since the leading coefficient is negative.
Learn more about parabola:
brainly.com/question/31142122
#SPJ11
Ethan's full backpack weighed too much. He took out a 4/8 pound electronic reader, a 2 ⅛ pound full bottle of water, and a ⅞ pound combination lock. Now the backpack weighs 8 ⅝ pounds. How much did the backpack weigh before Ethan took out the supplies? Number model
Answers
Answer:
see below
Step-by-step explanation:
We can just add up all of these fractions:
2 1/8 + 7/8 = 2 8/8 = 3
8 5/8 + 4/8 = 8 9/8 = 9 1/8
3 + 9 1/8 = \(12\frac{1}{8}\)