Need help asap) Judy took $30 with her to spend on popcorn and drinks for herself and her friends at the movie theater. The price for each bag of popcorn was $5. The price of each drink was half the price of a bag of popcorn. ( Questions) A: Sketch the graph that represents the situation and label the intercepts. Use one axis to represent the number of bags of popcorn and the axis to represent the number of drinks. B: Explain your graph. ( Need Help and Will Mark Brainliest).
Answers
Answer:
\(the \: porpcon \: intercept, \: p = (0, \: 5) \\ the \: drink \: intercept, \: p = (2.5, \: 0)\)
Step-by-step explanation:
\(let \: the \: price \: of \: each \: popcorn \: be : p \\ let \: the \: price \: of \: each \:drink \: be : d \\ \\ p = 5 \\ d = \frac{5}{2} = 2.5 \\ \\ explanation : \\ the \:p - intercept \: is \: the \: point \: were \: the \: line \: crosses \: the \: p - axis. \\ the \:d - intercept \: is \: the \: point \: were \: the \: line \: crosses \: the \: d - axis. \\ \\ \\ i \: believe \: with \: these \: information \:you \: can \: plot \: clear \: graph \: \)
Related Questions
If a truck averages 17 miles to the gallon, how many pounds of carbon dioxide are emitted into the atmosphere when the truck travels 236 miles?
Answers
Bob packs 13 pounds of nuts in bags. Each bag has 1/4 pound of nuts. Which equation shows the number of bags Bob packed with all the nuts?
13 × 1/4 = 52
13 ÷ 1/4 = 52
13 ÷ 1/4 = 14/4
13 × 1/4 = 13/4
Answers
The equation for the bag with all nuts is 13 / ( 1/4 ) = 52 bags
Given data ,
Bob packs 13 pounds of nuts in bags.
Each bag has 1/4 pound of nuts
Now , the number of bags = pounds of nuts / pounds of nuts in each bag
A = 13 / 1/4
On simplifying the equation , we get
A = 52 bags
Hence , the number of bags is 52 bags
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
Simplify.
510√
2√
2√2
10√2
5√
Answers
Answer:if you know how to do this your smart and in two years if someone can Answer ill give you a mil in cash swear
Step-by-step explanation:
Answer:
√10/2
Step-by-step explanation:
I took le test
PLEASE SOLVE THIS....I WILL GIVE BRAINLIEST!!!

Answers
Answer:
Give me a sec
Step-by-step explanation:
f(x) = 6^2+12x -7
please answer and explainnnn!

Answers

Answer:
A) \(x=-1\pm\sqrt{\frac{13}{6}}\)
Step-by-step explanation:
\(\displaystyle x=\frac{-12\pm\sqrt{12^2-4(6)(-7)}}{2(6)}\\\\x=\frac{-12\pm\sqrt{144+168}}{12}\\\\x=\frac{-12\pm\sqrt{312}}{12}\\\\x=\frac{-12\pm2\sqrt{78}}{12}\\\\x=-1\pm\frac{\sqrt{78}}{6}\\\\x=-1\pm\sqrt{\frac{78}{36}}\\\\x=-1\pm\sqrt{\frac{13}{6}}\)
36x^2=y^2
Does the equation define y as a function of x ?
Answers
Answer:
ya the equation divides y as a function of x
The graph of the function f(x) = -(x+3)(x-1) is
shown below.
-6
-4 -2
6
A
2
-2
4
-6
2
4
6 X
What is true about the domain and range of the
function?
O The domain is all real numbers less than or equali
to 4, and the range is all real numbers such that -31
≤x≤ 1.
The domain is all real numbers such that-3≤x≤
1, and the range is all real numbers less than or
equal to 4.
The domain is all real numbers, and the range is all
real numbers less than or equal to 4.
The domain is all real numbers less than or equal
to 4, and the range is all real numbers.
Answers
Using the concepts of domain and range of a function, the correct statement regarding the graph of the function f(x) = -(x + 3)(x - 1) is given by:
The domain is all real numbers, and the range is all real numbers less than or equal to 4.
What are the domain and the range of a function?The domain of a function is the set that contains all the values of the input.The range of a function is the set that contains all the values of the output.In a graph:
The domain is given by the x-values, the horizontal axis.The range is given by the y-values, the vertical axis.The graph of f(x) = -(x + 3)(x - 1) is given at the end of the answer, hence:
The domain is all real values, as the function keeps going to infinity.The range is all values of y that are less than or equal to 4.Hence the correct statement is:
The domain is all real numbers, and the range is all real numbers less than or equal to 4.
More can be learned about the domain and the range of a function at https://brainly.com/question/10197594
#SPJ1

True or False, please give me an answer asap, and a reasoning would also be great

Answers
Answer:
False
Reasoning:
- It's an acute angle, 140 is obtuse
- Angles 6 and 8 are 140 degrees, so 5 can't be
Answer:
False
Step-by-step explanation:
∠ 8=140° (alt. ext.∠)
∠5=180-140 (∠ on a str. line)
=40
≠140
A tank contains 100 gallons of pure water. At time zero, a sugar-water solution containing 0.2 lb of sugar per gallon enters the tank at a rate of 3 gallons per minute. Simultaneously, a drain is opened at the bottom of the tank allowing the sugar solution to leave the tank at 3 gallons per minute. Assume the solution in the tank is kept perfectly mixed at all times. What will be the eventual sugar content in the tank as time goes to infinity?
Answers
Answer:
20 lbs of sugar per gallon as time goes to infinity
Step-by-step explanation:
Because of the statement ... as time goes to infinity...I am inclined to approach this problem using derivatives and limits
Let the amount of sugar in the tank at any time t(in minutes) be
\(S(t) \;lbs/gal\)
We have \(S(0) = 0\) since the initial quantum of water has zero sugar
The inflow rate of sugar is given as 3 gal/min and each gallon contains 0.2 lbs of sugar
\therefore The rate of sugar increase in the tank n lbs/gal
= 0.2 lbs /gal \times 3 gal/min
= 0.6 lbs/min
Outflow rate = 3 gal/min
At any time t, the tank contains 100 gal
The amount of sugar at time t = \dfrac{S(t)}{100} lbs/gal
Therefore the outflow rate of sugar = 3 gal/min \times \dfrac{S(t)}{100} lbs/gal
= 0.03S(t) lb/min
The net rate is given by inflow rate - outflow rate
= 0.6 - 0.03S(t)
In calculus terms the net rate = \(\dfrac{dS(t)}{dt}\)
Therefore
\(\dfrac{dS(t)}{dt} = 0.6 - 0.03S(t)\)
\(\dfrac{dS(t)}{dt} - 0.03S(t) = 0.6\\\\\) (1)
A trick to solving differential equations of this type is to use the method of integrating factors
In general, if we have a differential equation of the type
\(\dfrac{dy}{dx} + Py = Q\\\\\)
where P and Q are functions only of x
then the integrating factor is \(e^{\int\ {P} \, dx }\)
which you use to multiply both sides of the differential equation first
In equation (1) above,
y = S(t) which well simply write as S for convenience
Writing S' for \(\dfrac{dS(t)}{dt}\) for convenience we get equation (1) as
\(S' + 0.03S =0.6\) (2)
From the above we see that P in the generalized differential equation corresponds to 0.03
Therefore the integrating factor is
\(\mbox {\large e^{\int 0.03dt} = e^{0.03t}}\)
Multiply equation (2) throughout by this integrating factor to get
\(\mbox{\large e^{0.03t} S' + 0.03S e^{0.03t} = 0.6 e^{0.03t} }\)
The left side is nothing but the first derivative of \(\mbox{\large (e^{0.03t}S) }\\\\\)
\(= \mbox{\large (e^{0.03t}S)'\\\\}}\)
Integrating both sides we get
\(\mbox{\large e^{0.03t}S = 0.06 \int e^{0.03t}dt}\\\\\) (3)
\(\textrm{By using the fact that $\int e^{ax} dx = \dfrac{e^{ax}}{a} + C$}:\\\\\mbox{\large \int e^{0.03t}dt} = \dfrac{e^{0.03}}{ 0.03}} + C\\\\\)
Therefore equation (3) becomes
\(e^{0.03t}S = 0.06 \cdot \dfrac{e^{0.03}}{0.03}} + C\\\\e^{0.03t}S = 0.06 \cdot 33.333 \cdot e^{0.03} + C\\\\e^{0.03t}S = 20 \cdot e^{0.03} + C\\\)
Dividing by \(e^{0.03} \textrm{ (same as multiplying by $e^{-0.03}$) both sides}\):
\(S = 20 + Ce^{-0.03t}\\\\\textrm{Plugging back S(t):}\\\\S(t) = 20 + Ce^{-0.03t}\\\)
We are asked to find the level of sugar content as t ⇒ ∞
At t = 0, S(t) = 0; there is no sugar content
S(0) = 0 = 20 + Ce⁰
0 = 20 + C
C = -20
\(S(t) = 20 -20e^{-0.03t}\\\\\)
As t ==> ∞
we get
\(\lim _{x\to \infty }S\left(t\right)=\:\lim _{x\to \infty }\left(20\:-\:20e^{-0.03t}\right)=\:\:20\:-\:0\:=\:20\)
Therefore as time goes to infinity the eventual sugar content
= 20 lbs/gallon
Need help!!! A rocket scientist is designing a rocket to visit the planets in the solar system. The velocity that is needed to escape a planet’s gravitational pull is called the escape velocity. The escape velocity depends on the planet’s radius and its mass, according to the equation V escape=square root(2gR where R is the radius and g is the gravitational constant for the particular planet. The rocket’s maximum velocity is exactly double Earth’s escape velocity. The earth’s gravitational pull is 9.8 m/s^2 The earth’s radius is 6.37 x10 ^6 For which planets will the rocket have enough velocity to escape the planet’s gravity?

Answers
Answer:
Mercury, Venus, Earth, Mars, and Uranus
Step-by-step explanation:
Calculate the escape velocity for each planet, using the equation v = √(2gR).
\(\left[\begin{array}{cccc}Planet&R(m)&g(m/s^{2})&v(m/s)\\Mercury&2.43\times10^{6}&3.61&4190\\Venus&6.07\times10^{6}&8.83&10400\\Earth&6.37\times10^{6}&9.80&11200\\Mars&3.38\times10^{6}&3.75&5030\\Jupiter&6.98\times10^{7}&26.0&60200\\Saturn&5.82\times10^{7}&11.2&36100\\Uranus&2.35\times10^{7}&10.5&22200\\Neptune&2.27\times10^{7}&13.3&24600\end{array}\right]\)
The rocket's maximum velocity is double the Earth's escape velocity, or 22,400 m/s. So the planets the rocket can escape from are Mercury, Venus, Earth, Mars, and Uranus.
6 more than a quotient of nine and a number p
Answers
Answer:
9/p+6
Step-by-step explanation:
Robert had 2 2/5 cups of chocolate syrup left in his freezer he used 1/4 cup of Chocolate syrup when he makes a milkshake what is the maximum number of milkshakes that Robert can make with the chocolate syrup

Answers
Robert can make a maximum of 8 milkshakes with the remaining chocolate syrup.
How to find the maximum number of milkshakes that Robert can make with the chocolate syrupConverting the mixed number 2 2/5 to an improper fraction: 2 2/5 = 12/5
Subtracting the amount of chocolate syrup used per milkshake from the total amount of chocolate syrup:
12/5 - 1/4 = (48 - 5) / 20 = 43/20
Therefore, Robert has 43/20 cups of chocolate syrup left, which is the maximum amount he can use to make milkshakes.
For maximum number of milkshakes:
(43/20) / (1/4) = (43/20) x (4/1) = 172/20 = 8.6
Since Robert cannot make a fraction of a milkshake, he can make a maximum of 8 milkshakes with the remaining chocolate syrup.
Learn more about word problems at https://brainly.com/question/21405634
#SPJ1
The data represents the heights of eruptions by a geyser.
Use the heights to construct a stemplot. Identify the two values that are closest to the middle when the data are sorted in order from lowest to highest.

Answers
The values nearest to these middle elements are 60 and 63 inches.
The dataset is given as:
62 33 50 90 80 50 40 70 50 63 74 53 55 64 60 60 78 70 43 82
Then, we sort the information elements in ascending request
33 40 43 50 50 50 53 55 60 60 62 63 64 70 70 74 78 80 82 90
The length of the dataset is 20.
Thus, the elements at the middle are the tenth and the 11 elements.
From the arranged dataset, these elements are: 60 and 62
Thus, the values nearest to this median are 60 and 63
to know more about the median click here:
https://brainly.com/question/14532771
#SPJ1
How does the value of the digit 3 in the number 63,297 compare to the value of the digit of 3 in the number 60,325? Be sure to include what you know about place value in your answer.
Answers
The solution is, the value of the digit 3 in the number 63,297 compare to the value of the digit of 3 in the number 60,325 is 2700.
Here, we have,
given that,
the value of the digit 3 in the number 63,297 compare to the value of the digit of 3 in the number 60,325.
we have,
The value of the digit 3 in the number 63,297 is 3,000 while the value of the digit 3 in the number 60,325 is 300.
we know,
the value of the digit 3 in the number 63,297 = 3000
the value of the digit 3 in the number 60,325 = 300
so, we get,
The difference between value of the digit 3 in the number 63,297 and the value of the digit 3 in the number 60,325 will be:
= 3000 - 300
= 2700
Hence, the value of the digit 3 in the number 63,297 compare to the value of the digit of 3 in the number 60,325 is 2700.
To learn more on subtraction click:
brainly.com/question/2346316
#SPJ1
How do I find the margin of error?
Answers
Answer:
You can find the margin of error by using this this formula
\(z \times \frac{σ}{ \sqrt{n} } \)
What do I do?
Brief Calculus Question: Find Each limit (if it exist)

Answers
For the given function the value of limits are
\(\lim _{x\to 0^-}\left(f\left(x\right)\right)\) is 5
\(\lim _{x\to 0^+}\left(f\left(x\right)\right)\) is 0
\(\lim _{x\to 0}\left x^2+5\)is 5
The given function is f(x)= x²+5, when x≤0
f(x)=2x when x>0
\(\lim _{x\to 0^-}\left(f\left(x\right)\right)\)
Which is \(\lim _{x\to 0^-}\left x^2+5\)
The given limit is a left hand limit as there is minus in the limits
When we apply x as 0 we get the value 5
Now \(\lim _{x\to 0^+}\left(f\left(x\right)\right)\)
So \(\lim _{x\to 0^+}\left 2x\)
The given limit is a right hand limit as there is positive in the limits
When we apply x as 0 we get 0
Now \(\lim _{x\to 0}\left(f\left(x\right)\right)\)
Which is \(\lim _{x\to 0}\left x^2+5\)
We get 5
To learn more on Limits click:
https://brainly.com/question/8533149
#SPJ1
What is the perimeter of the triangle?
a
84 in
b
94 in
c
74 in
d
64 in

Answers
Answer:
The answer is C
Step-by-step explanation:
We alsreadyknow that 37 and 12 is the 2 given lines. and The last line is not 37 but pretty close making C the answer.
Answer:
D) 64 In
Step-by-step explanation:
P=12+37+64
Approximate the integral
using midpoint rule, where n = 4.

Answers
The approximation for ∫₀¹\(e^{cos(x)}\)dx using midpoint rule is 2.345. Option B
How do we approximate the integral using midpoint rule?The midpoint rule is a numerical method for approximating the definite integral of a function which looks like
1. ∫ f(x) dx = ᵃΔx {f((x₀+x₁)/2) + f((x₁+x₂)/2) + f((x₂+x₃)/2) + .....+ f((xₙ₋₂+xₙ₋₁)/2 + f((xₙ₋₁+xₙ)/2)
Where Δx = (b-a)/n
f(x) = \(e^{cos(x)}\),
a = 0,
b = 1
n=4
we're dividing the interval [0, 1] into 4 subintervals.
Therefore Δx = (1-0)/4 = 1/4
Input this a = 0, 1/4, 1/2, 3/4, 1 = b, to the above formula, (1.)
1. a) f((x₀+x₁)/2
= f((0+1/4)/2) = f(1/8)
= \(e^{cos(1/8)}\) =2.697155413902143
1. b) f((x₁+x₂)/2)
= f((1/4+1/2)/2) = f(3/8)
= \(e^{cos(3/8)}\) = 2.535796076614806
1. c) f((x₂+x₃)/2)
= f((1/2+3/4)/2) = f(5/8)
= \(e^{cos(5/8)}\) = 2.250074033617969
1. d) f((x₃+x₂)/2)
= f((3/4+1)/2) = f(7/8)
= \(e^{cos(7/8)}\) = 1.898372344355632
We add the values of the 4 subintervals and multiply by 1/4
1/4(2.697155413902143 + 2.535796076614806 + 2.250074033617969 + 1.898372344355632) = 2.345.
Find more exercises on integrals;
https://brainly.com/question/14502499
#SPJ1
Solve the following system of equations.
-3x+5y=-7
-7x-9y=25
Answers
Answer:
(x,y)=(-1.-2)
Step-by-step explanation:
Using the elimination method:
-27x+45y=-63
-35x-45y=125
---------------------
-62x=62-->x=-1
-3*(-1)+5*6=-7-->y=-2
Calculate each compound event probability: a. X ≤ 15, n = 20, π = .70 (Round your answer to 4 decimal places.) b. X > 8, n = 11, π = .65 (Round your answer to 4 decimal places.) c. X ≤ 1, n = 13, π = .40 (Round your answer to 4 decimal places.)
Answers
For X ≤ 15, n = 20, π = .70 ; compound event probability is approximately 0.0008 .
For X > 8, n = 11, π = .65 ; compound event probability is approximately 0.9198.
For X ≤ 1, n = 13, π = .40 ; compound event probability is approximately 0.6646 .
a. To calculate the probability of the event X ≤ 15, n = 20, π = .70, we will use the binomial distribution formula:
P(X ≤ 15)
= ∑_(k=0)¹⁵〖(20Ck)(0.70)^k (0.30)^(20-k) 〗
Using a binomial distribution calculator, we can find this probability to be approximately 0.0008 (rounded to 4 decimal places).
b. To calculate the probability of the event X > 8, n = 11, π = .65, we will first find the probability of X ≤ 8, and then subtract this value from 1 to find the complement probability:
P(X > 8) = 1 - P(X ≤ 8)
= 1 - ∑_(k=0)⁸〖(11Ck)(0.65)^k (0.35)^(11-k)〗
Using a binomial distribution calculator, we can find the probability of X ≤ 8 to be approximately 0.0802.
Therefore, the probability of X > 8 is approximately 0.9198 (rounded to 4 decimal places).
c. To calculate the probability of the event X ≤ 1, n = 13, π = .40, we will use the binomial distribution formula:
P(X ≤ 1)
= ∑_(k=0)¹〖(13Ck)(0.40)^k (0.60)^(13-k)〗
Using a binomial distribution calculator, we can find this probability to be approximately 0.6646 (rounded to 4 decimal places).
For more such questions on event probability visit:
https://brainly.com/question/30390037
#SPJ8
ASAPPPPPPPPPPPPPPPPPPPPPP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
The sum will be close to 1/4
Step-by-step explanation:
1/8+1/6 is 7/24, and 1/4th of that is 6/24, so it is very close.
Answer: The sum will be close to 1/4
Step-by-step explanation:
You can start by making the fractions have the same denominator, (8*6) which gets you 48
You then want to use the butterfly method, so 1/8 becomes 6/48 and 1/6 becomes 8/48. You then add these up to 14/48.
12/48 is 1/4, and 14/48 is close to 12/48, thus making the answer the first option.
Please help with this math question!

Answers
Answer:
\(2000 {(1 + \frac{.07}{12}) }^{5 \times 12} = 2835.25\)
Susan subscribed to a video game rental service. She pays the same
amount for each video game she rents plus a monthly fee to subscribe to
the service. The cost for different numbers of video game rentals are
shown in the graph.

Answers
Answer:
C
Step-by-step explanation:
Answer: C. $6.00 monthly fee and $1.25 per video game
Step-by-step explanation:
I did the test
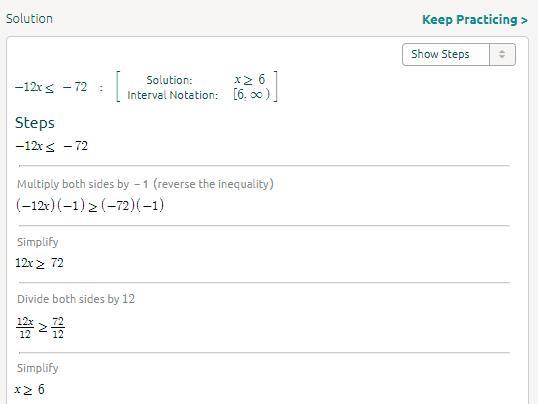
whats the solution to -12x ≤ -72
Answers
Answer:
I love algebra anyways
the ans is in the picture with the steps
(hope it helps can i plz have brainlist :D hehe)
Step-by-step explanation:

Answer:
Step-by-step explanation:
\( - 12x \leqslant - 72 \\ x \geqslant \frac{ - 72}{ - 12} \\ x \geqslant 6\)
The direction changes when we divide by nagative value
I hope that is useful for you :)
Someone help me pleasee

Answers
Step-by-step explanation:
Place one point at 3,-6 and the other at 5,-7
It doesn't matter where you place the second point, as long as the slope is -1/2. This means that the line goes one half down for every unit it goes to the right, so it goes down one unit when it goes two units to the right.
The table shows three unique, discrete functions.
x f(x) g(x) h(x)
-1
0
3
185
15
2
3
0
-25
-10-204
2
3
2
-3
2
3
4
5
6
Which statements can be used to compare the
characteristics of the functions? Select three options.
Of(x) has the greatest maximum.
h(x) has the greatest x-intercept.
g(x) has the smallest minimum value.
All three functions share the same domain.
All three functions share the same y-intercept.

Answers
All thre functions share the same y intercept
We can analyze the characteristics of the given functions based on the information provided in the table.
We cannot determine which function has the greatest maximum based on the table alone, as we do not have the complete graph of any of the functions.
We can see from the table that h(x) has an x-intercept of 0, which is the smallest among the three functions. Therefore, we can say that h(x) has the smallest x-intercept.
We can see from the table that g(x) has a minimum value of -204, which is the smallest among the three functions. Therefore, we can say that g(x) has the smallest minimum value.
We cannot determine if all three functions share the same domain based on the table alone. We can only see that all three functions have been evaluated at the same set of input values.
We can see from the table that the y-intercept of f(x) is 2, the y-intercept of g(x) is 3, and the y-intercept of h(x) is 4. Therefore, we can say that all three functions have different y-intercepts.
Therefore, the statements that can be used to compare the characteristics of the functions are:
h(x) has the smallest x-intercept.
g(x) has the smallest minimum value.
All three functions have different y-intercepts.
Based on the supply graph and the demand graph shown above, what is the price at the point of equilibrium?
Hint: Think about the point where they both meet. For example, if you were to place the graphs on top of each other, what would be the point of intersection?
Type the correct number below without the dollar sign.

Answers
Based on the supply graph and demand graph shown above, the price at the point of equilibrium is $ 30.
Demand refers to quantity of a commodity that the consumers are willing to, able to purchase at a given price during a given period of time. Supply refers to quantity of a commodity that the producers are willing to, able to offer for sale at a given price during a given period of time.
Demand curve slopes downward due to inverse relationship between price and quantity demanded whereas supply curve slopes upward due to direct relationship between quantity supplied and price. When both demand and supply curve intersect with each other balance is achieved. Intersection point between demand and supply curve is known as equilibrium.
At this point when prices are equal is known as equilibrium price and when quantiy demanded or supplied are equal it is known as equilibrium quantity. When we combine the given graph. Equilibrium is achieved at a point when price is equal to $ 30 and quantity is equal to 20 units.
To learn more about equilibrium of demand and supply:
https://brainly.com/question/30237240
3:Let f be a quadratic function such that
f(x) = ax² +bx+c = a (x-h)² + k
If k < 0, for what values of a will f(x) have no real zeros?
O a=0
O a<0
O azo
4.
O a>0
O aso
none of the answer choices

Answers
Answer:
O a=0
Step-by-step explanation:
1. Display the data in a matrix A with rows indicating years. What is element a 14?

Answers
Answer:
LOL i don't even know
Step-by-step explanation:
Answer:
63
Step-by-step explanation you just killed my brainmeats
A rectangular yard has a width that is 10 feet longer than the width . If the the area of the yard is 600 squared feet , find the dimension of the yard
Answers
Answer:
length = 30 feet and width = 20 feet
Step-by-step explanation:
Let l is length and b is width of a rectangular yard. The area of a rectangle is given by :
A = lb ..(1)
A rectangular yard has a length that is 10 feet longer than the width.
length, l = 10+b ...(2)
ATQ,
Put the value of l in equation (1),
\((10+b)b=600\\\\10b+b^2=600\\\\b^2+10b-600=0\\\\b^2+30b-20b-600=0\\\\b(b+30)-20(b+30)=0\\\\(b+30)(b-20)=0\\\\b=-30\ \text{feet}\ \text{and}\ b=20\ \text{feet}\)
Width can't be negative. The width is 20 feet.
Put the value of b is equation (2),
l = 10+20
l = 30 feet
Hence, the length and width are 30 feet and 20 feet.