Mrs. Wingate has 10 students in her math class. The line plot shows the number of hours students spent doing homework last week.
240 minutes
60 minutes
120 mintues
180 minutes
The median amount of time students spent on homework last week was how many minutes?

Answers
Answer:
The median amount of time students spent on homework last week was 180 minutes.
Step-by-step explanation:
The median is the middle value when all data values are placed in order of size.
If there is an even number of elements in the data set, the median is the average of the two middle numbers.
From inspection of the given dot plot, the number of hours the 10 students spent doing homework last week in order of size is:
2, 2, 3, 3, 3, 3, 4, 4, 5, 6The two middle numbers are 3 and 3. Therefore, the average of these two numbers is 3, so the median amount of time students spent on homework last week was 3 hours.
As there are 60 minutes in one hour:
⇒ 3 hours = 3 × 60 minutes = 180 minutes
Therefore, the median amount of time students spent on homework last week was 180 minutes.
Related Questions
Do number 3 pls and how to do it

Answers
A two-column proof to show that m∠3 + m∠6 = 180° should be completed with the statements and reasons stated below.
What is the consecutive interior angles theorem?In Mathematics and Geometry, the consecutive interior angles theorem states that when two (2) parallel lines are cut through by a transversal, the interior angles that are formed are congruent and each pair of the consecutive interior angles is supplementary.
In this context, a two-column proof to show that m∠3 + m∠6 = 180° should be completed with the following statements and reasons;
Statement Reasons
l║n Given
∠6 and ∠7 are linear pair consecutive interior angles theorem
∠3 ≅ ∠7 Definition of linear pair
m∠3 + m∠6 = 180° Substitution property
Read more on consecutive interior angles theorem here: https://brainly.com/question/24607467
#SPJ1
HELP ME PLEASE
I NEED HELP ASAP
IF IM ABLE TO GIVE OUT BRAINLIST THEN I WILL GIVE IT




Answers
The manager can find the volume of the container using the formula lwh. The employee correctly determines that the container can be filled with 3 layers of 21. He can find the volume of the container by multiplying the number of bento boxes that fill the container by the volume of one bento box. The volume found by using the formula is equal to the volume of the total numberof bento boxes in the container.
How to calculate the volume of a rectangular prism?In Mathematics and Geometry, the volume of a rectangular prism can be calculated by using the following formula:
Volume of a rectangular prism = LWH
Where:
L represents the length of a rectangular prism.W represents the width of a rectangular prism.H represents the height of a rectangular prism.Part a.
Therefore, the manager can use the following formula;
Volume of container = LWH
Volume of container = 7/2 × 3/2 × 3/2
Volume of container = 63/8 cm³.
Part b.
For the number of bento boxes that can fill the container, we have:
Number of bento boxes = Volume of container/Volume of bento boxes
Number of bento boxes = 63/8/(1/2)³
Number of bento boxes = 63/8/1/8
Number of bento boxes = 63/8 × 8
Number of bento boxes = 63 bento boxes = 3 layers × 21.
Part d.
Volume of container = Volume of bento boxes
63/8 cm³ = 63 × 1/8 cm³
63/8 cm³ = 63/8 cm³ (equal).
Read more on volume of prism here: brainly.com/question/21012007
#SPJ1
Find the value of x, 6,4, 3x, 4x+1

Answers
Answer:
If two chords intersect in a circle, then the product of the segments of one chord equals the product of the segments of the other chord.
6(3x) = 4(4x + 1)
18x = 16x + 4
2x = 4
x = 2
Can someone please hope and show the work?

Answers
Answer: 16 pounds of grain.
Step-by-step explanation: 36 divided by 9 is 4, which means we have to multiply bin C by how much bin J was multiplied by, which is 4, so 4x4 is 16.
(let me know if you would like me to explain more on this)
15 POINTS!
Sarah had $100 dollars in her bank account, and she spent $88 dollars on concert tickets. How much money is left in her account?
Answers
wow way to manage momey here sarah
I don't know if I'm right or not. I think it's C, but I'm not too sure.
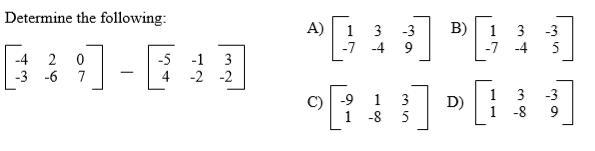
Answers
Answer:
its c
Step-by-step explanation:
Answer:
Ya its c
Step-by-step explanation:
It's correct u can cliuck or do it without any fear best of luck
Delta makes 12-volt car batteries. These batteries are known to be normally
distributed with a mean of 45 months and a standard deviation of 8 months.
What percent of Delta car batteries last between three and four years?
Answers
Answer:
The probability that Delta car batteries last between three and four years
P(36≤X≤48) = 0.5188
The percentage of that Delta car batteries last between three and four years
P(3≤X≤4) = 52%
Step-by-step explanation:
Step(i):-
Given that the sample size n =12 -volt car batteries
Let 'X' be a Random variable in a normal distribution
Given that mean of the normal distribution = 45 months
Given that the Standard deviation of the normal distribution = 8months
Step(ii):-
Let X₁ = 3 years = 12 × 3 = 36 months
\(Z_{1} = \frac{x_{1} -mean}{S.D} = \frac{36-45}{8} = -1.125\)
Let X₂ = 4 years = 12 × 4 = 48 months
\(Z_{2} = \frac{x_{2} -mean}{S.D} = \frac{48-45}{8} = 0.375\)
Step(iii):-
The probability that Delta car batteries last between three and four years
P(36≤X≤48) = P(-1.125≤Z≤0.375)
= P(Z≤0.375) - P(Z≤-1.125)
= 0.5 +A(0.375) - (0.5-A(1.125)
= 0.5 + 0.1480 - (0.5 -0.3708)
= 0.1480 + 0.3708
= 0.5188
Final answer:-
The probability that Delta car batteries last between three and four years
P(36≤X≤48) = 0.5188
The percentage of that Delta car batteries last between three and four years
P(3≤X≤4) = 52%
Where are the minimum and maximum values for f(x)=−2+4cosx on the interval [0,2π]?
Answers
Answer:
\(f(x) = - 2 + 4 \cos(x) \\ for \: minimum \: \: x = 0 \\ f(0) = - 2 + 4 \cos(0) \\ minimum \: value = 2 \\ for \: maximum \: value \: \: x = 2\pi \\ f(2\pi) = - 2 + 4 \cos(2\pi) \\ maximum \: value = - 2\)
The function is minimum at 3π/2 and the function is maximum at 0 and 2π.
What is the maximum and minimum value of the function?The condition for the maximum will be
f(x)'' < 0
The condition for the minimum will be
f(x)'' > 0
The function is given below.
f(x) = −2 + 4cosx
Differentiate the function with respect to x, then we have
f'(x) = − 4 sin x
Again differentiate the function with respect to x, then we have
f''(x) = − 4 cos x
Then the minimum value of the function will be
f'(x) = 0
−4 sin x = 0
sin x = 0
The value of f''(x) is positive in the interval of (π/2, 3π/2). Then the value of x will be
x = π
Then the maximum value of the function will be
And the of f''(x) is negative in the interval of [0,2π] – (π/2, 3π/2). Then the value of x will be
x = 0 and 2π
More about the maximum and minimum value of the function link is given below.
https://brainly.com/question/13581879
#SPJ5
If you had to make a real-life decision involving debt, what would you do differently as a result of playing the game?
Answers
Answer:
cry about it
Step-by-step explanation:
crying will help you feel worse and think about paying for all your debts.
When a person agrees with another party or the lender from whom he/she has taken a certain amount of funds or when the performance is due then it is said to be debt.
The debtor needs to pay a certain value to the lender in the given time.
To pay the debt that the person accumulated was due to playing games so, to repay the debt that person needs to earn money.
The person can work part-time jobs or can look for real work based on his qualifications.
In this way, the debt can be paid in small amounts or installments.
The person should avoid playing games that involve gambling by tightly restricting himself by self-control.
To learn more about debt follow the link:
https://brainly.com/question/12198015
The profile of the cables on a suspension bridge may be modeled by a parabola. The central span of the bridge is 1210 m long and 128 m high. The parabola y equals 0.00035 x squared gives a good fit to the shape of the cables, where StartAbsoluteValue x EndAbsoluteValue less than or equals 605, and x and y are measured in meters. Approximate the length of the cables that stretch between the tops of the two towers.
Answers
Answer:
The approximated length of the cables that stretch between the tops of the two towers is 1245.25 meters.
Step-by-step explanation:
The equation of the parabola is:
\(y=0.00035x^{2}\)
Compute the first order derivative of y as follows:
\(y=0.00035x^{2}\)
\(\frac{\text{d}y}{\text{dx}}=\frac{\text{d}}{\text{dx}}[0.00035x^{2}]\)
\(=2\cdot 0.00035x\\\\=0.0007x\)
Now, it is provided that |x | ≤ 605.
⇒ -605 ≤ x ≤ 605
Compute the arc length as follows:
\(\text{Arc Length}=\int\limits^{x}_{-x} {1+(\frac{\text{dy}}{\text{dx}})^{2}} \, dx\)
\(=\int\limits^{605}_{-605} {\sqrt{1+(0.0007x)^{2}}} \, dx \\\\={\displaystyle\int\limits^{605}_{-605}}\sqrt{\dfrac{49x^2}{100000000}+1}\,\mathrm{d}x\\\\={\dfrac{1}{10000}}}{\displaystyle\int\limits^{605}_{-605}}\sqrt{49x^2+100000000}\,\mathrm{d}x\\\\\)
Now, let
\(x=\dfrac{10000\tan\left(u\right)}{7}\\\\\Rightarrow u=\arctan\left(\dfrac{7x}{10000}\right)\\\\\Rightarrow \mathrm{d}x=\dfrac{10000\sec^2\left(u\right)}{7}\,\mathrm{d}u\)
\(\int dx={\displaystyle\int\limits}\dfrac{10000\sec^2\left(u\right)\sqrt{100000000\tan^2\left(u\right)+100000000}}{7}\,\mathrm{d}u\)
\(={\dfrac{100000000}{7}}}{\displaystyle\int}\sec^3\left(u\right)\,\mathrm{d}u\\\\=\dfrac{50000000\ln\left(\tan\left(u\right)+\sec\left(u\right)\right)}{7}+\dfrac{50000000\sec\left(u\right)\tan\left(u\right)}{7}\\\\=\dfrac{50000000\ln\left(\sqrt{\frac{49x^2}{100000000}+1}+\frac{7x}{10000}\right)}{7}+5000x\sqrt{\dfrac{49x^2}{100000000}+1}\)
Plug in the solved integrals in Arc Length and solve as follows:
\(\text{Arc Length}=\dfrac{5000\ln\left(\sqrt{\frac{49x^2}{100000000}+1}+\frac{7x}{10000}\right)}{7}+\dfrac{x\sqrt{\frac{49x^2}{100000000}+1}}{2}|_{limits^{605}_{-605}}\\\\\)
\(=1245.253707795227\\\\\approx 1245.25\)
Thus, the approximated length of the cables that stretch between the tops of the two towers is 1245.25 meters.
HELP WITH C
5mph buffer what is the new function and graph?

Answers
The function for fine at every speed should be doubled in construction zones is f(n)= -8.75n+637.5.
What is the function?Functions are the fundamental part of the calculus in mathematics. The functions are the special types of relations. A function in math is visualized as a rule, which gives a unique output for every input x.
The coordinate points from the graph are (10, 550) and (30, 200).
Here, slope = (200-550)(30-10)
= -350/20
= -35/2
= -17.5
Substitute m= -17.5 and (x, y)=(10, 550) in y=mx+c, we get
550=-17.5(10)+c
c=550+175
c=725
So, the equation is y= -17.5x+725
Thus, f(n)= -17.5n+725
a) The fine at every speed should go up by $10.
So, the coordinates are (10, 560) and (30, 210)
New slope (m)= (210-560)(30-10)
= -350/20
= -35/2
= -17.5
Substitute m= -17.5 and (x, y)=(10, 560) in y=mx+c, we get
560=-17.5(10)+c
c=550+175
c=735
So, the equation is y= -17.5x+735
Thus, f(n)= -17.5n+735
b) The fine at every speed should be doubled in construction zones.
So, the coordinates are (20, 550) and (60, 200)
New slope (m)= (200-550)(60-20)
= -350/40
= -8.75
Substitute m= -8.75 and (x, y)=(20, 550) in y=mx+c, we get
550=-8.75(10)+c
c=550+87.5
c=637.5
So, the equation is y= -8.75x+637.5
Thus, f(n)= -8.75n+637.5
Therefore, the function for fine at every speed should be doubled in construction zones is f(n)= -8.75n+637.5.
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ1

Identify the solution set 3c-5-c=7+4c
Answers
2c - 5 = 4c + 7
Now to subtract 4c from both sides:
-2c - 5 = 7
Next, we add 5 to both sides:
-2c = 12
Finally, divide both sides by the coefficient:
c = -6
Find the equation of the line specified. The slope is -4, and it passes through ( 5, 8).
a. y = 4x + 8
b. y= -4x + 28
C. y = -4x - 12
d. y= -8x + 28
Please select the best answer from the choices provided A W B C С D
Answers
Answer:
B. y= -4x + 28
Step-by-step explanation:
To find the equation of this line first put it into slope-point form, \(y-y_{1} =m(x-x_{1})\) where \(y_{1}\) and \(x_{1}\) are the y and x coordinates and m is the slope. So plug in the information to get the equation, y-8=-4(x-5). Then solve for y,
First, distribute the -4
y-8=-4x+20
Next, add 8 to both sides
y=-4x+28
The expression 12x + 6 can be used
to describe a sequence algebraically. Which of the following could be the first
five numbers in this sequence?
A 6, 12, 18, 24, 30
B 6, 18, 24, 36, 42
C 18, 30, 42, 54, 66
D 18, 36, 54, 72, 90
Answers
The first five terms of the given sequence are:
C: 18, 30, 42, 54, 66
How to find the nth term of a sequence?The formula for the nth term of an arithmetic sequence is expressed as:
aₙ = a + (n - 1)d
where:
a is first term
d is common difference
n is number of term
The formula for the sequence is 12x + 6. Thus:
First term = 12(1) + 6 = 18
Second term = 12(2) + 6 = 30
Third term = 12(3) + 6 = 42
Fourth term = 12(4) + 6 = 54
Fifth term = 12(5) + 6 = 66
Thus, the sequence is : 18, 30, 42, 54, 66
Read more about nth term of sequence at: https://brainly.com/question/7882626
#SPJ1
The mean of the data set is 4. Find the absolute deviation of each of the red data values
The absolute deviation of 0 is
The absolute deviation of 3 is
The absolute deviation of 7 is

Answers
The absolute deviation of each of the data values are 4, 1 and 3 respectively.
Absolute deviationThe absolute deviatuon gives the distance of any given value in a dataset to the mean value. The absolute deviation is always positive as it does not consider the side to which the value belongs.
Absolute deviation = |value - mean|
Mean = 4
Absolute deviation of 0 = |0 - 4| = 4
Absolute deviation of 3 = |3 - 4| = 1
Absolute deviation of 7 = |7 - 4| = 3
Hence, The absolute deviation of each of the data values are 4, 1 and 3 respectively.
Learn more on absolute deviation : https://brainly.com/question/29545538
#SPJ1
In the command window in MATLAB generate a random 6 x 6 matrix with integer entries using the command G = round(10* rand(6)) For each of the following questions below, execute the given commands and match the result with the best explanation of how MATLAB got the answer (some explanations will not match). G(:,:) G(:) G(7,6) ✓ [Choose ] maximum entry in each column of G reshapes all elements of G into a single column vector assigns the value 4 to all entries of G that are greater than 4 reshapes the matrix G into a single row vector returns the matrix G in its original form maximum entry in each row of G returns an indexing error entries of G that are greater than 4 sum of the entries in each column of G sum of the entries in each row max(G) sum(G) [ Choose ] G(G>4) [Choose ] G(G>4)=4 [Choose]
Answers
G(:,:) returns the matrix G in its original form. This command takes all elements of G and reshapes them into a single row vector. This means that all elements of G are included in the output, and the output is in the same shape as the original matrix.
G(:) reshapes all elements of G into a single column vector. This command takes all elements of G and places them into a single column. This means that all elements of G are included in the output, and the output is in a column vector.
G(7,6) returns an indexing error. This command attempts to access an element outside of the range of the matrix G. Since G is a 6 x 6 matrix, there is no element at the index (7,6).
max(G) returns the maximum entry in each column of G. This command takes the maximum value from each column and returns them as a single row vector. This means that the output contains the maximum value from each column and the output is in a single row vector.
sum(G) returns the sum of the entries in each column of G. This command takes the sum of all entries in each column and returns them as a single row.
Learn more about MATLAB:
https://brainly.com/question/27854252
#SPJ4
ITS DO TODAY HELPPPPPPP

Answers
The difference in the addition of both fractions is that they have different lowest common multiples.
How to solve Fraction Problems?We want to add the fraction expression given as:
¹/₂ + ¹/₄
Taking the Lowest common multiple of 8, we have:
(4 + 2)/8 = 6/8
However, for the second fraction expression, we have:
¹/₂ + ¹/₃
Taking the lowest common multiple which is 6, we have:
(3 + 2)/6 = 5/6
Read more about Fraction Problems at: https://brainly.com/question/24132459
#SPJ1
Order from least to greatest.
6/11 , 1.5, 0.545, 1/2
Answers
Answer:
1/2 < 0.545 < 6/11 < 1.5
Step-by-step explanation:
I used calculator soup order sorter.
please help!! And show work please.
Apartment A requires a $300 security deposit and costs $750 each month. Apartment B has a $500 security deposit and the monthly rent is $725. Write and solve an equation to find the number of months it will take for the total rental costs to be the same.
Answers
500- 300 = 200
750 - 725 = 25
200÷ 25 = 8
it will take them 8 months for the total rent to cost the same
11) Tell whether (3, 20) is a solution of y = 4x +8 A) Yes B) No
Answers
y = 4x + 8
To tell if (3, 20) is a solution, we will substitute the value of x = 3 and y= 20
into the equation to see if the left-hand side equals the right-hand side of the equation
So, upon substituting
20 = 4 x 3 + 8
20 = 12 + 8
20 = 20
Since the left-hand side of the equa
Select all ratios equivalent to 3:2.
2:1
7:16
21:14
Answers
Answer:
Step-by-step explanation:
21 : 14
Both have 7 in common
3 : 2
So Option C 21 : 14 is the correct answer
HELP PLEASE whats the number for this answer?
ASAP

Answers
Answer:
68°
Step-by-step explanation:
Total angle in a quadrant = 90°
x + 22° = 90°
x = 90 - 22
x = 68°
Kendra reads in Modern Dog Magazine that the average age of dogs currently alive is 4.8 years. To determine if this finding applies to the customers in her pet store, Kendra surveys every fifth customer in her store who owns a dog and asks the age of their dog. She collects data for seven weeks and obtains the following averages.
Week Average Age (in years)
1 3.7
2 3.8
3 4.2
4 4.1
5 3.9
6 3.9
7 4.0
Select the statement that is true about Kendra's sample.
a) Kendra's samples are both accurate and precise.
b) Kendra's samples are precise but not accurate.
c) Kendra's samples are neither accurate nor precise.
d) Kendra's samples are accurate but not precise.
Answers
Answer:
The true statement about Kendra's sample is:
b) Kendra's samples are precise but not accurate.
Step-by-step explanation:
a) Data and Calculations:
Average age of dogs currently alive = 4.8 years
Average ages of dogs in Kendra's sample
Week Average Age (in years)
1 3.7
2 3.8
3 4.2
4 4.1
5 3.9
6 3.9
7 4.0
Total 27.6
Mean = 3.9 (27.6/7)
b) Accuracy refers to how close Kendra's sample mean age of dogs is to the average age value as stated in the Modern Dog Magazine. While the Magazine stated an average age of 4.8 years, Kendra's sample produced a mean of 3.9 years. On the other hand, precision refers to how close Kendra's sample measurements are to each other. With a mean of 3.9 years, the sample measurements are very close to each other. Therefore, we can conclude that "Kendra's samples are precise but not accurate."
Answer:
Kendra's samples are precise but not accurate.
Step-by-step explanation:
To be accurate and precise they should be around 4.8 for all the measures. We can see that they are all relatively close to one another (between 3.7 and 4.2), so they are precise. However, they are all are smaller than 4.8, so they are not accurate.
A gym membership charges $50 new member fee and $24 for every month after. Write an equation for this where y is the total cost and x is the number of months attended.
Answers
Answer:
y=24x+50
24= per month
x= months attended
50=member fee
Faith ate 1/3 of an apple pie for lunch the next day she had part of the apple pie for a snack after her snack there was 1/4 of the apple pie remaining how much of the apple pie did faith eat for her snack
Answers
Answer:
5/12
Step-by-step explanation:
convert 1/3 into 4/12 and subtract 4/12 out of 12/12
you get 8/12. then you subtract 5/12 from it because it will remain 3/12 and 3/12=1/4.
Gianna drives 5 miles in 10 minutes. If she drove three hours in total at the same rate,
how far did she go?
Before you try that problem, answer the question below.
How many minutes did Gianna drive in total?
Answers
Gianna is 90 miles far away in 3 hours of driving.
She drove in total of 180 minutes.
What is speed?The speed can be defined as the rate at which an object covers some distance. Speed can be measured as the distance traveled by a body in a given period of time. The SI unit of speed is m/s.
Given,
Gianna drives 5 miles in 10 minutes
Speed per minute = 5/10 = 0.5 miles/minute
Gianna drove in total for 3 hours
1 hour = 60 minutes
3 hours = 60 × 3 = 180 minutes
Distance Gianna drove in 180 minutes = speed per minute × time
= 0.5 × 180
= 90 miles
Hence, Gianna drove 90 miles in 3 hours, 180 minutes is total time she drove.
Learn more about speed here:
https://brainly.com/question/28224010
#SPJ1
(8 2/3 - 3 1/2) x (4 1/6+2 1/3)
Answers

Please help
x2 + 14x + 37 = 0
Answers
Answer:
x = −37/16
This is the value of x which completes the equation properly, unless you mean x^2 instead of x2.
For positive integer n, the factorial notation n! represents the product of the integers from n to 1. (For example, 6!= 6.5.4.3. 2. 1.) What value of N satisfies the following equation? 5!.9!= 12. N! (A)10 (B)11 (C)12 (D)13 (E)14
Answers
The value of N that satisfies the following equation, 5!9!= 12N!, is 10.
Factorial notation (n!) means to multiply a series of descending natural numbers. Also stated in the problem that for positive integer n, the factorial notation n! represents the product of the integers from n to 1.
Take for example 6! which can be written as 6 x 5 x 4 x 3 x 2 x 1 = 720.
Given the equation 5!9!= 12N!, expand the factorial notation.
(5 x 4 x 3 x 2 x 1)(9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1) = (4 x 3) N!
N! = (5 x 2 x 1)(9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1)
N! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
N = 10
Therefore, the value of N that satisfies the following equation, 5!9!= 12N!, is 10.
Learn more about factorial here: https://brainly.com/question/16868621
#SPJ4
Consider the following sets of sample data:A: $31,100, $25,800, $36,300, $30,200, $30,000, $19,800, $22,300, $22,600, $34,900, $21,700, $36,900, $30,800, $31,700, $37,100B: 3.18, 4.24, 4.27, 4.38, 3.87, 4.75, 3.43, 3.35, 4.16, 4.81, 2.98Step 1 of 2 : For each of the above sets of sample data, calculate the coefficient of variation, CV. Round to one decimal place.
Answers
The coefficient of variation for A is 20.37% and for B is 15.98%.
What is coefficient of variation?
In statistics, the relative standard deviation (RSD), commonly referred to as the coefficient of variation formula (CV), is a standardized way to assess how widely spaced out a probability distribution or frequency distribution is. Lower values of the coefficient of variation indicate that the data is highly stable and less variable.
We know that formula for coefficient of variation is
CV = Standard Deviation / Mean
A. $31,100, $25,800, $36,300, $30,200, $30,000, $19,800, $22,300, $22,600, $34,900, $21,700, $36,900, $30,800, $31,700, $37,100
Mean = 411200 / 14
Mean = $29371.42
Similarly,
Standard Deviation = $5984.52
So,
CV = 5984.52 / 29371.42 * 100
CV = 20.37%
B. 3.18, 4.24, 4.27, 4.38, 3.87, 4.75, 3.43, 3.35, 4.16, 4.81, 2.98
Mean = 43.42 / 11
Mean = $3.94
Similarly,
Standard Deviation = $0.63
So,
CV = 0.63 / 3.94 * 100
CV = 15.98%
Hence, the coefficient of variation for A is 20.37% and for B is 15.98%.
Learn more about coefficient of variation from the given link
https://brainly.com/question/30783938
#SPJ1