melissa ran "m" meters per second, and jasmine ran "j" meters per second. They ran for "t" seconds. The expression t(m-j) describes how many more meters melissa ran than jasmine ran during that time. We can also use the expression tm-tj to represent the same quantity. explain how the expression t(m-j) and tm-tj are equivalent.
Answers
Answer:
tm-tj is just the expansion of t(m-j)
Step-by-step explanation:
To show how they are equivalent it would be best to substitute values for t, m and j.
Let t = 5
Let m = 2
Let j = 1
tm-tj = t(m-j)
5x2 - 5x1 = 5(2-1)
10 - 5 = 5(1)
5 = 5
Therefore tm-tj = t(m-j)
Related Questions
suppose that you are dealt 5 cards from a well shuffled deck of cards. what is the probability that you receive a hand with exactly three suits
Answers
Probability of receiving a hand with exactly three suits \(= (4 * (13^3)) / 2,598,960\)
What is Combinatorics?
Combinatorics is a branch of mathematics that deals with counting, arranging, and organizing objects or elements. It involves the study of combinations, permutations, and other related concepts. Combinatorics is used to solve problems related to counting the number of possible outcomes or arrangements in various scenarios, such as selecting items from a set, arranging objects in a specific order, or forming groups with specific properties. It has applications in various fields, including probability, statistics, computer science, and optimization.
To calculate the probability of receiving a hand with exactly three suits when dealt 5 cards from a well-shuffled deck of cards, we can use combinatorial principles.
There are a total of 4 suits in a standard deck of cards: hearts, diamonds, clubs, and spades. We need to calculate the probability of having exactly three of these suits in a 5-card hand.
First, let's calculate the number of favorable outcomes, which is the number of ways to choose 3 out of 4 suits and then select one card from each of these suits.
Number of ways to choose 3 suits out of 4: C(4, 3) = 4
Number of ways to choose 1 card from each of the 3 suits\(: C(13, 1) * C(13, 1) * C(13, 1) = 13^3\)
Therefore, the number of favorable outcomes is \(4 * (13^3).\)
Next, let's calculate the number of possible outcomes, which is the total number of 5-card hands that can be dealt from the deck of 52 cards:
Number of possible outcomes: C(52, 5) = 52! / (5! * (52-5)!) = 2,598,960
Finally, we can calculate the probability by dividing the number of favorable outcomes by the number of possible outcomes:
Probability of receiving a hand with exactly three suits =\((4 * (13^3)) / 2,598,960\)
This value can be simplified and expressed as a decimal or a percentage depending on the desired format.
To know more about Combinatorics visit:;
https://brainly.com/question/28065038
#SPJ4
Joe started 125 miles in 5 hours. How many miles would travel in 1 hour
Answers
Answer:
Hope this helps :D
Step-by-step explanation:
Explanation on picture

this is a test pls help me I only have a limited of time!

Answers
Answer:
Step-by-step explanation:
By process of elimination we see that only D or E could be correct. Now to find the angle o, we must subtract
360- 150 - 150 = 60
Now we divide that between angle o and m and... we get 30!
The answer is... angle j is 150 and angle o is 30
The population of rabbits on an island is growing
exponentially. In the year 1990) the population of rabbits
was 190, and by 1994 the populştion had grown to 280.
Predict the population of rabbits in the year 2001, to the
nearest whole number.
Answers
Answer:
770
Step-by-step explanation:
280 divided by 4 = 70 so every year is 70 year increase
770 but it asked to round so by 2001 it increased to 770
Answer:
c
Step-by-step explanation:
xxxxx
What is the area of the shaded region?

Answers
Answer:
208
Step-by-step explanation:
4*30 = 120
(15-4) * 8 = 88
88 + 120 = 208
Answer:
208 cm
Step-by-step explanation:
Solving right side first. 8*15=120
Take out 8cm from 30. 30 - 8 = 22
22*4= 88
88 + 120 = 208
Check work I found the total area and the white rectangle.
15*30=450 which in total area
15-4=11 11 is the left/right side of the white rectangle
30-8=22 22 is the top/bottom side of the white rectangle.
22*11= 242
208+242=450
The volume of calls, V( h), at a particular customer service center can be written as a function of the number of hours after opening each day, h. What would the ordered pair (6,8) represent for this function?
Answers
The ordered pair (6,8) represents the number of calls made after the customer service center opened for 6 hours.
Given that the volume of calls, V( h), at a particular customer service center can be written as a function of the number of hours after opening each day, h. So, (6,8) means that the center has been opened for 6 hours and that there have been 8 calls during this period. It represents the value of the volume of calls V(6) which is 8. Therefore, after opening the customer service center for 6 hours, 8 calls were made.
This function has a direct relationship between the number of hours after opening the center and the number of calls made. Therefore, the longer the center is open, the more calls are expected to be received, and vice versa.
Learn more about ordered pair here:
https://brainly.com/question/30805001
#SPJ11
Solve the equation
3(4z-7)=-21+12z
Answers
Answer:
Step-by-step explanation:
Let's open the brackets,
12z - 21 = -21 + 12z (distributive property)
12z - 12z = -21 + 21
0z = 0
z = 0
Please help me with my homework!!!

Answers
Answer:
C
Step-by-step explanation:
Plug the values into the function
Two cubical boxes of side a cm are placed next to one another to form a cuboid. The total surface area of the cuboid so formed is?
Answers
Answer: 60
Step-by-step explanation:
Alex writes down a decimal number. Grogg writes down one tenth of Alex's problem. Winnie writes down one hundredth of Alex's problem. the product of all 3 monsters' numbers is 0.000008. what is Alex's number

Answers
Let x represent Alex's number.
Then Grogg wrote down 1/10 · x = x/10 = 0.1x.
Winne write down 1/100 · x = x/100 = 0.01x
The product of all three is:
(x)(0.1x)(0.01x) = 0.001x^3
0.001x^3 = 0.000008
Multiplying by 1000 on both sides we have:
x^3 = 0.008
x = cuberoot(0.008)
x = 0.2
Alex's number is 0.2, Grogg's is 0.02, and Winnie's is 0.002.
How much would the volume of this cube decrease if you reduced the length of each side by 3 cm?
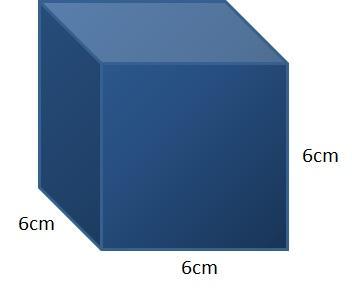
Answers
Answer:
Original volume: 6^3 = 216 cubic cm
New volume: 3^3 = 27 cubic cm
The volume of this cube would decrease by 189 cubic centimeters if the length of each side was reduced from 6 cm to 3 cm.
Describe a sequence of transformations that shows that Polygon A is
congruent to Polygon B.
Answers
Answer:
25
Step-by-step explanation:
10 2.5 16 4 ? 7.5 48 12 Which statement explains how to find the number of minutes it takes to bike 7.5 miles? Find the ratio of minutes to miles, 4:1. Divide 7.5 by 4. Find the ratio of minutes to miles, 4:1. Multiply 7.5 by 4. Find the difference between 16 and 10. Add the difference to 16. Find the difference between 16 and 10. Add the difference to 7.5.
Answers
Answer:
Find the ratio of minutes to miles, 4:1. Multiply 7.5 by 4.
Step-by-step explanation:
Given
Minutes: 10 || 16 || ? || 48
-----Miles: 2.5 || 4 || 7.5 || 12
Required
Which statements solve for the missing value?
First, we need to calculate the ratio of minutes to mile
\(Ratio = \frac{Minutes}{Mile}\)
When minutes = 16; mile = 4
So, we have:
\(Ratio = \frac{16}{4}\)
\(Ratio = 4\)
Next, we multiply the ratio by 7.5
\(Minutes = Ratio * 7.5\)
\(Minutes =4 * 7.5\)
\(Minutes = 30\)
Hence, option B answers the question.
Select all the expressions that are equivalent to -8.
80
100
800
100
80 = (-10)
-80 = (-10)
480
-100
end of first quarter today, this is due today. please help! :)

Answers
Answer:
-800/100 and 80 ÷ (–10)
Step-by-step explanation:
I did the test and I got 100%
HI HELP ME PLEASEEE!’

Answers
We're given
(0, 144)
(1, 48)
(2, 16)
(3, 16/3)
\(f(x) = a*b^x\\144 = a*b^0\\144 = a\\\)
now that we know a, we can find b
\(f(x) = 144*b^x\\48 = 144*b\\b = \frac{48}{144}\\b = \frac{1}{3}\)
\(f(x) = 144*(\frac{1}{3})^x\)
find the equation of locus of all points equidistant from the point +2,4 )and y-axis
Answers
Answer:
Let P(h,k) be the point which is equidistant from the point (2,4) and the y-axis. The distance of point P(h,k) from the y-axis is h. ∴h=√(h−2)2+(k−4)2⇒h2−4h−4+k2−8k+16=h2⇒k2−4h−8k+20=0.
Hence,the locus of (h,k)is y2−4x−8y+20=0.
Step-by-step explanation:
In the diagram, the measures of 22, 23 and 26 are 40°. The measure of 21
is 140°. Are lines cand d parallel?

Answers
Answer:
c. Yes because ∠2 and ∠6 are congruent.
Step-by-step explanation:
From the picture attached,
m(∠2) = m(∠3) = m(∠6) = 40°
m(∠1) = 140°
Since (∠2 ≅ ∠6) (corresponding angles)
Therefore, by the converse theorem of corresponding angles lines c and d are parallel.
Option c is the answer.
Please help me with edge question .

Answers
\(~\hspace{7em}\textit{negative exponents} \\\\ a^{-n} \implies \cfrac{1}{a^n} ~\hspace{4.5em} a^n\implies \cfrac{1}{a^{-n}} ~\hspace{4.5em} \cfrac{a^n}{a^m}\implies a^na^{-m}\implies a^{n-m} \\\\[-0.35em] ~\dotfill\\\\ (4)^{\frac{-4}{2}} \implies (4)^{-2}\implies 4^{-2}\implies \cfrac{1}{4^2}\implies \cfrac{1}{16}\)
Please help me find the quadratic inequality for this
y ≥ x2 - 4x + 1
Answers
Answer:
x/> -y/2 + 1/2
A sign says that the price marked on all music equipment is 40% off the original price. You buy a drum set for the sale price of $870.What percent of the original price is the sale price?
Answers
Answer:
870 X 40% = $338.00
The original price was $1208.00
The price was marked with the discount already
40%
Step-by-step explanation:
Is this a function yes or no

Answers
Answer:
Yes
Step-by-step explanation:
Draw a vertical line anywhere on the graph. If it hits 2 points, then it's not.
I also attached an example when a graph is not a function
See how it hits two point on the graph?
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K


find the measures of the angles of the triangle whose vertices are a = ( − 2,0), b = (2,1), and c = (1, − 2).
Answers
So the triangle has three equal angles of 60 degrees.
To find the measures of the angles of the triangle with vertices at (-2,0), (2,1), and (1,-2), we can use trigonometry.
Let's use the following notation:
a = (-2,0)
b = (2,1)
c = (1,-2)
First, we need to find the coordinates of the midpoint of line segment AB, which is the length of the hypotenuse of the triangle.
Using the Pythagorean theorem, we have:
\(c^2 = a^2 + b^2\\1^2 + (-2)^2 = 2^2 + 1^2\)
25 = 4 + 1
23 = 3
So the length of the hypotenuse is 3 units.
Next, we need to find the coordinates of the midpoint of line segment BC, which is the length of one of the legs of the triangle.
Again, using the Pythagorean theorem, we have:
\(b^2 = a^2 + c^2\\1^2 + (-2)^2 = 2^2 + 1^2\)
25 = 4 + 1
23 = 3
So the length of the leg of the triangle is 3 units.
Now, we can use the law of cosines to find the measures of the angles of the triangle.
Let's denote the angle between lines AB and BC as alpha, the angle between lines AB and AC as beta, and the angle between lines BC and AC as gamma.
Using the law of cosines, we have:
\(cos(alpha) = (b^2 + c^2 - a^2) / (2bc)\\cos(beta) = (a^2 + c^2 - b^2) / (2ac)\\cos(gamma) = (a^2 + b^2 - c^2) / (2ab)\)
We know that:
a = (-2,0)
b = (2,1)
c = (1,-2)
So we can substitute these values into the above equations:
\(cos(alpha) = (2^2 + (-2)^2 - (-2)^2) / (2(-2)1) = (2 + (-2) + 2) / (2(-2)1) = 4 / 3\\cos(beta) = ((-2)^2 + 2^2 - (-2)^2) / (2(-2)2) = (-2 + 4 + 2) / (2(-2)2) = -1\\cos(gamma) = (2^2 + 1^2 - 1^2) / (2(1)(-2)) = 2 + (-1) + (-1) / (2(1)(-2)) = 1\)
Now we can substitute these values into the Pythagorean theorem to find the length of the legs of the triangle:
sin(alpha) = length of leg 1 / (2bc)
sin(beta) = length of leg 2 / (2ac)
sin(gamma) = length of leg 2 / (2ab)
We know that:
a = (-2,0)
b = (2,1)
c = (1,-2)
So we can substitute these values into the above equations:
sin(alpha) = √(8) / (2(-2)1)
= √(8) / √(3)
= √(2)
sin(beta) = √(5) / (2(1)2)
= √(5) / √(3)
= √(2)
sin(gamma) = √(5) / (2(1)(-2))
= √(5) / 1
= √(5)
Therefore, the measures of the angles of the triangle are:
alpha = 60 degrees
beta = 60 degrees
gamma = 60 degrees
So the triangle has three equal angles of 60 degrees.
Learn more about triangle visit: brainly.com/question/28470545
#SPJ4
Susan goes to an amusement park. The admission price to the park is $5. The cost per ride is $4. The total cost Susan spent in the amusement park is $29. How many rides did Susan go on?
Answers
Answer:
x = 6 rides
Step-by-step explanation:
4x + 5 = 29
4x = 29-5
4x = 24
x = 24/4
Franco is a very busy professional DJ. Last year, he worked 8 weddings and 26 other events. What is the probability that one of the events Franco worked last year, selected at random, was a wedding?
Answers
The probability that one of the events Franco worked last year, selected at random, was a wedding is equals to the \( \frac{4}{17} \).
Franco is a professional DJ and he was very busy in work during Last year. Number of events where he worked = 26
Number of wedding where he worked
= 8
So, total events where he played his DJ
= 26 + 8 = 34
We have to determine probability that one of the events Franco worked last year, selected at random, was a wedding.
Now, one of event is Randomly selected from all of above events. Number of favourable outcomes for worked on wedding events = 8
So, probability of selected a wedding event \( = \frac{8}{34} \)
\( = \frac{4}{17} \). Hence the required probability value is \( \frac{4}{17} \).
For more information about probability, visit:
https://brainly.com/question/25870256
#SPJ4
8+3x−2y−3 equivalent equation
Answers
The equivalent equation is 3x − 2y + 5.
What is the equation?The equation is defined as mathematical statements that have a minimum of two terms containing variables or numbers that are equal.
What are Arithmetic operations?Arithmetic operations can also be specified by the subtract, divide, and multiply built-in functions.
- Subtraction operation: Subtracts the right-hand operand from the left-hand operand.
for example 4 -2 = 2
Given that equation as:
⇒ 8 + 3x − 2y − 3
Rearrange the terms and apply arithmetic operations
⇒ 3x − 2y + 8 − 3
⇒ 3x − 2y + 5
Hence, the equivalent equation is 3x − 2y + 5.
Learn more about the equation here:
brainly.com/question/13947055
#SPJ1
Does 2 equal square root?
Answers
Therefore , it means if an equation have 2 roots , it means it is a quadratic function .
How to define square root ?The outcome of multiplying a number by itself produces the original number, which is the square root of that number. Squares and square roots are a few of examples of exponents. Try to visualize nine. Furthermore, this can be written as 3x3.
Here,
A quadratic function is one where an equation has two roots.
A quadratic function's two roots are equal if D=0.
D (discriminant) = 0 such that b24ac = 0 is needed in order for the roots of a polynomial function to be equal.
As a result, if an equation has two roots, a quadratic function is what it is.
To know more about square root , visit
brainly.com/question/29286039
#SPJ4
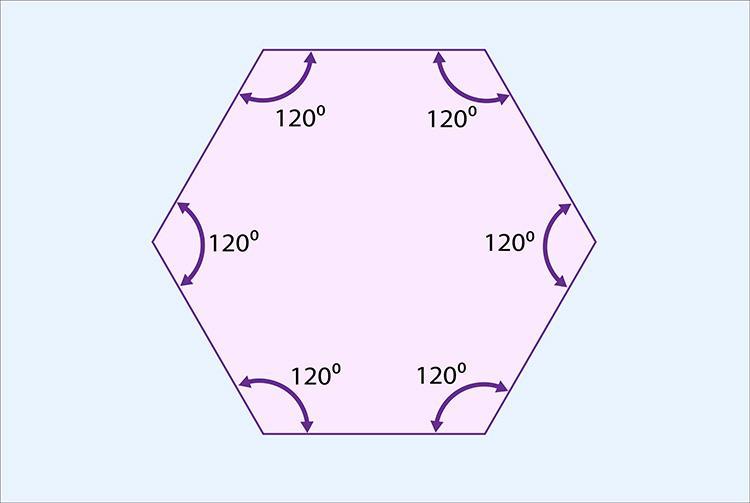
Find the sum of the interior angles for a hexagon. 540° 720° 900° 1,080°
Answers
The sum of interior Angles of Hexagon is always 720°
Any hexagon's internal angles add up to 720° in all cases. By dividing 720° by 6, we may get the size of each interior angle of a regular hexagon. As a result, we have:
720°÷6 = 120°
In a regular hexagon, each inside angle is 120°.
An example of a regular hexagon with equal-length sides and angles is shown in the diagram below. By multiplying the six 120° angles together, we can demonstrate that the result is 720°.
Therefore, the interior angles of a hexagon are always added up to 720°.
Learn more about hexagon :
brainly.com/question/3295271
#SPJ4
In which interval does a root exist for this equation? tan(x) = 3x^2
PLEASE HELP

Answers
To determine the interval for which a root exists, you can use the intermediate value theorem.
First, observe that the left-hand side of the equation, tan(x), is undefined for x = (n + 1/2) π, where n is an integer. Thus, we can restrict our attention to the interval (-π/2, π/2) where the tangent function is continuous and strictly increasing.
Next, note that tan(0) = 0 and tan(π/6) = 1/√3 < 3/36 = 1/12. Also, as x approaches π/2 from the left, tan(x) approaches infinity, while 3x^2 approaches infinity faster. Therefore, there exists at least one root of the equation in the interval (0, π/6).
Similarly, tan(-π/6) = -1/√3 > -1/12, and as x approaches -π/2 from the right, tan(x) approaches negative infinity, while 3x^2 approaches infinity faster. Therefore, there exists at least one root of the equation in the interval (-π/6, 0).
Therefore, the equation tan(x) = 3x^2 has at least one root in the interval (-π/6, π/6).
Suppose the points shown on the coordinate plane are vertices of a rectangle. Which statements are correct? A) The perimeter of the rectangle is 14 units. B) The perimeter of the rectangle is 28 units. C) The coordinates for the fourth vertex of the square are (5, 5). D) The coordinates for the fourth vertex of the rectangle are (−5, −6). E) The coordinates for the fourth vertex of the rectangle are (−5, −3).

Answers
Answer:
A
Step-by-step explanation:
Answer:
I beleive it is A and C i just took the test!
Step-by-step explanation:
yourwelcome! :)
2. The following set of count readings was made in a gradient-free γ-ray field, using a suitable detector for repetitive time periods of one minute: 18,500;18,410; 18,250;18,760;18,600;18,220;18,540;18,270;18,670;18,540. (a) What is the mean value of the number of counts? (b) What is its standard deviation (S.D.)? (c) What is the theoretical minimum S.D. of the mean? (d) What is the actual S.D. of a single reading? (e) What is the theoretical minimum S.D. of a single reading?
Answers
The inflection point of f(t) is approximately t = 3.73.
(a) To determine if the function f(t) = -0.425t^3 + 4.758t^2 + 6.741t + 43.7 is increasing or decreasing, we need to find its derivative and examine its sign.
Taking the derivative of f(t), we have:
f'(t) = -1.275t^2 + 9.516t + 6.741
To determine the sign of f'(t), we need to find the critical points. Setting f'(t) = 0 and solving for t, we have:
-1.275t^2 + 9.516t + 6.741 = 0
Using the quadratic formula, we find two possible values for t:
t ≈ 0.94 and t ≈ 6.02
Next, we can test the intervals between these critical points to determine the sign of f'(t) and thus the increasing or decreasing behavior of f(t).
For t < 0.94, choose t = 0:
f'(0) = 6.741 > 0
For 0.94 < t < 6.02, choose t = 1:
f'(1) ≈ 14.982 > 0
For t > 6.02, choose t = 7:
f'(7) ≈ -5.325 < 0
From this analysis, we see that f(t) is increasing on the intervals (0, 0.94) and (6.02, ∞), and decreasing on the interval (0.94, 6.02).
(b) To find the inflection point of f(t), we need to find the points where the concavity changes. This occurs when the second derivative, f''(t), changes sign.
Taking the second derivative of f(t), we have:
f''(t) = -2.55t + 9.516
Setting f''(t) = 0 and solving for t, we find:
-2.55t + 9.516 = 0
t ≈ 3.73
Therefore, The inflection point of f(t) is approximately t = 3.73.
Learn more about inflection point here:
https://brainly.com/question/29249123
#SPJ11