Melanie cuts a rectangle out of a piece of scrap paper as shown. She wants to calculate the angle measure of the piece that is left over. What is the measure in degrees?
Answers
Related Questions
A King in ancient times agreed to reward the inventor of chess with one grain of wheat on the first of the 64 squares of a chess board. On the second square the King would place two grains of wheat, on the third square, four grains of wheat, and on the fourth square eight grains of wheat. If the amount of wheat is doubled in this way on each of the remaining 30 squares, how many grains of wheat should be placed on square ? Also find the total number of grains of wheat on the board at this time and their total weight in pounds. (Assume that each grain of wheat weighs 1/7000 pound.)
Answers
The number of grains on square 13 will be 4096 grains.
How to calculate the number of grain?No. of grains on the first square = 1 = 2^0
No. of grains on the second square = 2 = 1*2 = 2¹
No. of grains on the third square = 4 = 2*2 = 2²
No. of grains on the fourth square = 8 = 2*4 = 2³
From the pattern it could be seen that amount of wheat is doubled for every next square
So, the number of grains in the nth square = 2^n-1
Therefore, No. of grains on 13th square
= 2^13 -1
= 4096
Learn more about sequence on:
https://brainly.com/question/6561461
#SPJ1
Soledad buys 5 ounces of frozen yogurt for $2.25. What is the unit price of the frozen yogurt in dollars per ounce?
Answers
Answer:
0.45
Step-by-step explanation:
You divided 2.25 by 5
hence, you divide 2.25 by 5.
solve 3(3+3) + 3(3+3)
Answers
Answer:
3×6 + 3×6 =36
Step-by-step explanation:
3 multiply 3+3 = 3*6 =18×2 =36
Answer:
Step-by-step explanation:
=3(3+3)+3(3+3)
=3x6+3x6
=18+18
=36
I hope this helps
Pls mark as Brainliest
What is the inverse of the function f(x)=5x+7−−−−−√3?
Answers
Answer:
The inverse function can be written as:
g(x) = (x - 7 + √3) / 5
Step-by-step explanation:
Starting with the equation y = 5x + 7 - √3, we switch the roles of x and y to get x = 5y + 7 - √3.
Next, we isolate y by subtracting 7 and adding √3 to both sides, which gives x - 7 + √3 = 5y.
Finally, we divide both sides by 5 to get g(x) = (x - 7 + √3) / 5.
This is the inverse function g(x) of f(x) = 5x + 7 - √3. The inverse function is useful in solving problems where the original function is not explicitly invertible.
Determine whether the function T is a linear transformation.
(a) T : R^3 → R^3 given by T(x, y, z) = (x + 1, y + 1, z + 1)
(b) T : Mn,n → R given by T(A) = trace(A) = a11 + a22 + · · · + ann.
(c) T : R^2 → R^2 given by T(x, y) = (1 + x, y
Answers
(a) Yes, T is a linear transformation.
(b) No, T is not a linear transformation.
(c) Yes, T is a linear transformation.
(a) To determine whether T is a linear transformation, we need to check two conditions: additivity and homogeneity. In this case, T(x, y, z) = (x + 1, y + 1, z + 1) satisfies both conditions.
It preserves addition since T(x₁ + x₂, y₁ + y₂, z₁ + z₂) = (x₁ + x₂ + 1, y₁ + y₂ + 1, z₁ + z₂ + 1) = (x₁ + 1, y₁ + 1, z₁ + 1) + (x₂ + 1, y₂ + 1, z₂ + 1) = T(x₁, y₁, z₁) + T(x₂, y₂, z₂). It also preserves scalar multiplication since T(c⋅x, c⋅y, c⋅z) = (c⋅x + 1, c⋅y + 1, c⋅z + 1) = c⋅(x + 1, y + 1, z + 1) = c⋅T(x, y, z). Therefore, T is a linear transformation.
(b) For T to be a linear transformation, it should preserve both addition and scalar multiplication. However, in this case, T(A) = trace(A) = a11 + a22 + · · · + ann only satisfies the condition of preserving addition. It fails to preserve scalar multiplication because T(c⋅A) = c⋅(a11 + a22 + · · · + ann) ≠ c⋅T(A). Hence, T is not a linear transformation.
(c) Similar to part (a), we need to verify additivity and homogeneity for T to be a linear transformation.
T(x, y) = (1 + x, y) satisfies both conditions. It preserves addition since T(x₁ + x₂, y₁ + y₂) = (1 + (x₁ + x₂), y₁ + y₂) = (1 + x₁, y₁) + (1 + x₂, y₂) = T(x₁, y₁) + T(x₂, y₂). It also preserves scalar multiplication since T(c⋅x, c⋅y) = (1 + c⋅x, c⋅y) = c⋅(1 + x, y) = c⋅T(x, y). Therefore, T is a linear transformation.
For more questions like Linear transformation click the link below:
https://brainly.com/question/13595405
#SPJ11
Select all the expressions that are equivalent to the number in the picture

Answers
Answer:
The expressions 10³÷10⁷, 10¹²/10¹⁶, and 10⁻²/10² are all equivalent to 10⁻⁴.
Step-by-step explanation:
When dividing exponents with the same base you subtract the exponents.
For visuals, in the equation 10³÷10⁷ it would be 10³⁻⁷ which would be 10⁻⁴ since 3 minus 7 is negative 4.
It is the same thing for 10¹²/10¹⁶, it would be 10¹²⁻¹⁶ which is equal to 10⁻⁴.
The same method can be used for 10⁻²/10² (10⁻²⁻²).
in xy plane, the unit circle with center at the origin o contains point a with 1,0 and point b with (3/5, 4/5)
Answers
Point A (1, 0) and point B (3/5, 4/5) both lie on the unit circle with center at the origin.
A circle is a geometric shape defined as the set of all points in a plane that are equidistant from a fixed point called the center. The distance between any point on the circle and the center is called the radius.
Center: The center is a fixed point in the plane from which all points on the circle are equidistant. It is denoted by the coordinates (h, k), where h represents the x-coordinate and k represents the y-coordinate of the center.
Radius: The radius is the distance between the center of the circle and any point on the circle. It is denoted by the letter "r". The radius is constant for all points on the circle.
Diameter: The diameter is a line segment passing through the center of the circle and with endpoints on the circle. It is twice the length of the radius, and it divides the circle into two equal halves.
In the xy-plane, the unit circle with center at the origin (0, 0) is defined by all the points that are at a distance of 1 unit from the origin.
Point A: (1, 0)
Point A lies on the x-axis and is 1 unit away from the origin. It represents a point on the unit circle.
Point B: (3/5, 4/5)
Point B lies on the unit circle but is not one of the standard points (such as (1, 0), (-1, 0), (0, 1), or (0, -1)). Instead, it represents a point on the unit circle with coordinates (3/5, 4/5). The x-coordinate of B is 3/5, and the y-coordinate is 4/5. The distance between point B and the origin (0, 0) is 1 unit, which satisfies the condition of being on the unit circle.
Therefore, point A (1, 0) and point B (3/5, 4/5) both lie on the unit circle with center at the origin.
To know more about radius visit:
https://brainly.com/question/31831831
#SPJ11
25% discount, the price of a t shirt was 15$. What was the price before the discount
Answers
The charge for the t-shirt earlier than the cut price of 25 percent is $20.
What is percentage?A value or ratio that may be stated as a fraction of 100 is referred to as a percentage in mathematics. If we need to compute a percentage of a number, we should divide it by its whole and then multiply it by 100. The proportion, therefore, refers to a component per hundred. Per 100 is what the term percent signifies. The letter "%" stands for it.
Given, the 25% discount, the price of a t-shirt was 15$.
Since, After 25% discount price of t-shirt = 15
Thus
Original price of t-shirt = 15 * 100/75
Original price of t-shirt = 20
Therefore, the price before the discount of 25 percent is $20.
Learn more about percentages here:
https://brainly.com/question/29306119
#SPJ
How do you write radicals in simplest form?.
Answers
Factor the radicand: If the radicand is not already in the form of a perfect square, you can factor it into its prime factors and pull out any perfect squares from the radicand.
For example, √(36) can be simplified to √(49) = √4 * √9 = 23.
Simplify the exponent: If the radical has an exponent (such as cube root), divide the exponent by the index of the radical. Example ∛64 = ∛(4^3) = ∛4 * ∛4 * ∛4 = 4 *4 *4 =4
Combine like factors: If there are any factors in the radicand that match the exponent, you can combine them and simplify the radical further. For example, √(2235) = √(2^235) = 2√(35) = 2√15 = 2*3 = 6.
It is important to note that not all radicals can be simplified to a whole number or a fraction. In some cases, the radical will be in its simplest form when it is left as an irrational number.
For Example, √2 cannot be simplified further.
To learn information about Exponent questions:
https://brainly.com/question/30066987
#SPJ4
marital status: of women according to the statistical abstract of the united states, 70.3% of females ages 20 to 24 have never been married. choose 5 young women in this age category at random. find the probability that a. none has ever been married
Answers
0.1717 is Probability that none has ever been married from selected 5 young women in age category at random.
In the question we have,
the number of females age 20 to 24 has never been married = 70.3%
the number of young women in this age category (20 to 24) at random = 5
We shall find out the probability that none has been maaried from selected group of 5 females.
Probability of female age 20 to 24 has never been married = 0.703
So, the probability that none has been married from selected group of 5 females ( p)= 0.703×0.703×0.703×0.73×0.73
= 0.1717
Therefore, The probability that none has ever been married is 0.1717.
To learn more about Probability, refer:
https://brainly.com/question/25870256
#SPJ4
Decoding METARKJAX 102320Z 1100/1124 00000KT P6SM SCT035 FM110300 00000KT 5SM BR BKN010 BKN020 FM110600 16003KT 2SM BR BKN005 OVC010 TEMPO 1108/1112 1SM BR OVC003 FM111400 20010G18KT P6SM VCSH BKN015 OVC025 FM111700 24014G23KT 5SM -SHRA OVC015FM?
Answers
Decoding Forecast starting at 17:00Z:
Wind:
24014G23KT
Visibility:
5 statute miles
Weather:
Light rain showers
Clouds:
Overcast at 1500 feet
Incomplete report.
The decoded report is:
Location:
KJAX (Jacksonville International Airport)
Date/Time: 10th at 23:20Z
Wind:
00000KT
Visibility:
More than 6 statute miles
Clouds:
Scattered at 3500 feet
Forecast starting at 11:00Z:
Wind:
00000KT
Visibility:
5 statute miles
Weather:
Mist
Clouds:
Broken at 1000 feet, Broken at 2000 feet
Forecast starting at 06:00Z:
Wind:
16003KT
Visibility:
2 statute miles
Weather:
Mist
Clouds:
Broken at 500 feet, Overcast at 1000 feet
Temporary condition between 08:00Z and 12:00Z:
Visibility:
1 statute mile
Weather:
Mist
Clouds:
Overcast at 300 feet
Forecast starting at 14:00Z:
Wind:
20010G18KT
Visibility:
More than 6 statute miles
Weather:
Vicinity showers
Clouds:
Broken at 1500 feet, Overcast at 2500 feet
For similar questions on Decoding
https://brainly.com/question/29168785
#SPJ11
Pls help and show workings due ASAP

Answers
Answer:
A
Step-by-step explanation:
By triangle inequality,
L < 15+6
15 < L+6
6 < L+15
Solving these, we get 9 < L < 21.
Only 10 falls within the range.
The answer is therefore 10cm i.e. A.
Radius ; 8,7 feet; height: 16 feet
Answers
Therefore , the solution of the given problem of volume comes out to be
the volume of cylinder is 3801.6 cubic feet.
Define volume.The amount of space a three-dimensional item occupies is measured by its volume, which is measured in cubic units. Two examples of cubic units are cm3 and in3. Mass, in contrast hand, is a metric of how much matter is present in an object. It is common to use the weight of an object to calculate mass in quantities like pounds or kilograms.
Here,
Given :
Radius = 8.7 feet
and height = 16 feet
To find the volume of cylinder :
=> πr²h
=> 22/7 * 8.7 * 8.7 * 16
=> 237.6 * 16
=> 3801.6 cubic feet.
Therefore , the solution of the given problem of volume comes out to be
the volume of cylinder is 3801.6 cubic feet.
To know more about volume , visit:
https://brainly.com/question/13338592
#SPJ1
The complete question is: "Find the volume of cylinder which hase Radius ; 8.7 feet; height: 16 feet ."
In the opening hour of a new store, a bell rang every 2 min and lights flashed every 3 min. If the store opened at 10 o’clock, at what times did both events happen at the same time? Explain or sketch a diagram to show the strategy you used.
Answers
Answer:
6 minutes past 10
Step-by-step explanation:
lowest common multiple of 2 and 3: 6 minutes
Solve (−7) ⋅ (−4). Please hurry :D
-28
-11
28
11
Answers
Answer:
28
Step-by-step explanation:
\( - (7) \times ( - 4) \\ - ( - 28) \\ - \times - = + \\ = 28\)
Raise to the power:
\((-xn)^{4}\)
Answers
Answer:
x^4 n^4
Step-by-step explanation:
(-x)^4*n^4
4 is an even power and the minus sign disappears. 4 minus signs make a plus.
x^4 n^4
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
\(( { - xn})^{4} = ({ - x})^{4} \times ({n})^{4} = \)
\(( { - 1})^{4} \times {x}^{4} \times {n}^{4} = {x}^{4} {n}^{4} \)
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
Please explain and show work. In the function f(x)=cosx, f(x) is multiplied by a factor of 3, x is replaced with 4x and 5 is added to the function. Explain the effects this has on the graph of the function (i.e. horizontally, vertically, compressed, stretched, etc.).
Answers
Your graph will actually look like an oscillation (wave), it will be more compressed horizontally. As the value of x increases withe very whole number, your graph will compress horizontally. More like in the image below.

Based on the areas of the squares determine whether the triangle shown is a right triangle
Answers
Answer:
The answer is "triangle ABC is not a right triangle".
Step-by-step explanation:
For a right-angle triangle:
Its square upon on longest or triangular edges is equivalent to the total of the other two squares
Its parameters indicated throughout the question are;
Square of lateral length \(A = 7 \ inch^2\)
The square of lateral length \(B = 18 \ inch^2\)
The square of lateral length \(C=27\ inch^2\)
Thus, the longest side is C, as well as the size \(inch^2\) of the squares of its two sides, is\(7 + 18 = 25 \ inch^2\), lower than square \(C = 27\ inch^2\), hence, the ABC triangle is not correct. Its longest edge is consequently C.

When Mr. Krumm purchased a tie he paid $\$9.27$, which included the $3\%$ sales tax. How many dollars did the tie cost before the tax was included
Answers
Mr. Krumm paid $9.27 for a tie that had a 3% sales tax added on. So, the tie cost $231.75 before the tax was included.
To find out how much the tie cost before the tax was included, we need to first calculate how much of the total price was due to the tax. We know that the total price Mr. Krumm paid was $9.27, and that this price included a $3% sales tax.
To calculate the amount of tax that was included in the price, we can start by setting up an equation:
0.03x = 9.27 - x
Here, x represents the cost of the tie before the tax was included. We know that the tax is 3% of this cost, which is why we're multiplying it by 0.03.. We're also subtracting x from 9.27 to get the amount of tax that was added on.
Simplifying this equation, we get:
0.04x = 9.27
Dividing both sides by 0.04, we get:
x = 231.75
So the tie cost $231.75 before the tax was included.
In summary, Mr. Krumm paid $9.27 for a tie that had a 3% sales tax added on. To find out how much the tie cost before the tax was included, we set up an equation and solved for the cost of the tie (x) before the tax was added. The answer is that the tie cost $231.75 before the tax was included.
Know more about the sales tax
https://brainly.com/question/30109497
#SPJ11
write the equation of the line that contains the following points in standard form (16,-3),(-4,12)
Answers
Answer:
y = -3/4x + 9
Step-by-step explanation:
first, find the slope by taking the difference of the y-values / difference of the x-values
(-3-12) / (16-(-4)) which equals -15/20 or -3/4
now use that value to represent the 'm' in the formula in order to find 'b'
y = mx + b
-3 = -3/4(16) + b
-3 = -12 + b
9 = b
y = -3/4x + 9
The sum of three prime numbers is 22. What is the largest possible product of these numbers?
Answers
Step-by-step explanation:
a+b+c=22
abc=?
2+3+17=22
2×3×17=102
Answer:
The numbers are 2, 7 and 13
Step-by-step explanation:
2+7+13 = 22
2X7X13 = 182
An adult gerbil at Fish 'n' weighed 1/5 lb. A young gerbil weighed 1/4 of that amount. How many did the young gerbil weigh?
Answers
A rectangular aquarium fish tank is 10.2 meters long, 5.8 meters wide, and 3.5 meters deep. What is the volume of the fish tank if the top 1/3 is just air
Answers
The volume of the water in the fish tank is 135.27 cubic meters if the top 1/3 of the tank is just air.
To find the volume of the fish tank containing water, we need to find the volume of the fish tank and then subtract the volume that is occupied by the air i.e 1/3 of the volume of the tank.
So, the volume of the fish tank is :
=length x width x depth of the tank
=10.2 meters x 5.8 meters x 3.5 meters
= 203.94 cubic meters
Now we need to find the volume of the air that is occupied by the fish tank which is :
=1/3x the volume of the fish tank
=1/3x203.94 cubic meters
=68.67 cubic meters
The volume of the fish tank containing just water is:
=volume of the fish tank - the volume of the air occupied
= 203.94 cubic meters - 68.67 cubic meters
=135.27 cubic meters
Learn more about Volume at:
https://brainly.com/question/1972490
IF YOU ANSWER THIS RIGHT NOW ILL GIVE YOU 64 POINTS
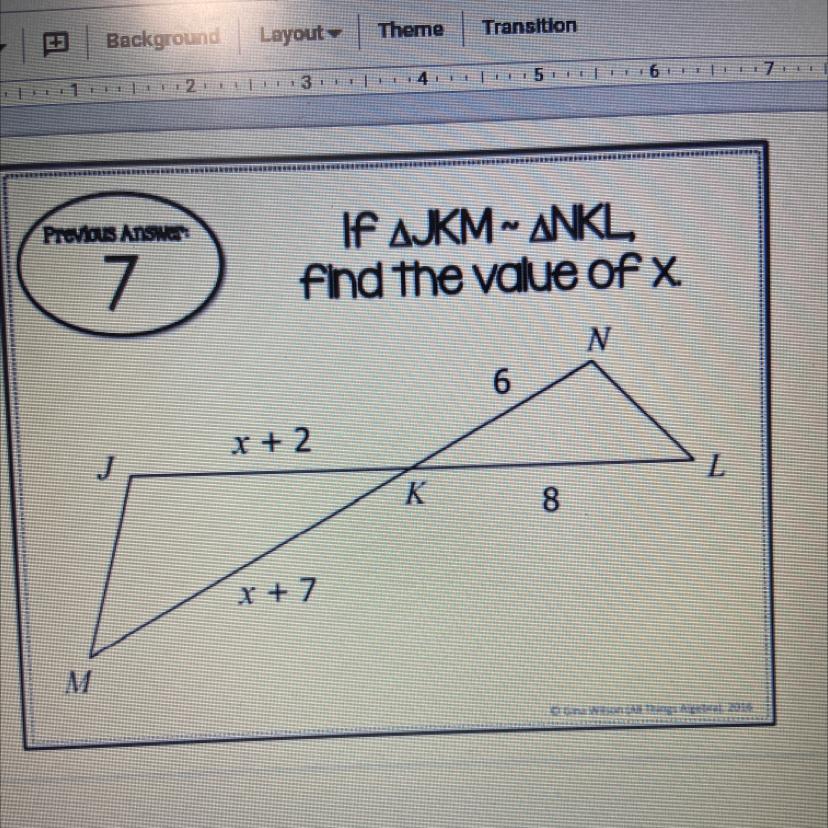
Answers
Answer:
13 = x
Step-by-step explanation:
\(\frac{6}{8}\) = \(\frac{(x + 2)}{(x + 7)}\)
6x + 42 = 8x + 16
42 = 2x + 16
\(\frac{26}{2}\) = \(\frac{2x}{2}\)
13 = x
6 ⁒ 2(1+2)=?
is the answer 1?
Answers
Answer:
9
Step-by-step explanation:
no, I don't think so because 6/2=3 and in the bracket 1+2=3 and if we multiple them then the answer should be 9 (3×3=9)
The answer to your question is 9 !
If P(B)=0.3,P(A∣B)=0.5,P(B ′ )=0.7, and P(A∣B ′ )=0.8, find P(B∣A).
Answers
If P(B)=0.3, P(A|B)=0.5, P(B')=0.7and P(A|B')=0.8, then the value of the probability P(B|A)= 0.2113
To find the value of P(B|A), follow these steps:
The probability of B given A can be given by the product of the probability of A given B and the probability of B, divided by the total probability of B. So, the formula for P(B|A) = P(A|B) * P(B) / [P(A|B)*P(B)+P(A|B')*P(B')]. Substituting the values, we get P(B|A) = (0.5) (0.3) / [(0.5) (0.3) + (0.8) (0.7)] ⇒P(B|A) = 0.15 / [0.15 + 0.56] ⇒P(B|A) = 0.15 / 0.71 ⇒P(B|A) = 0.2113. Therefore, P(B|A) = 0.2113.Learn more about probability:
brainly.com/question/13604758
#SPJ11
write an equation for a parabola with a vertex of (-1, -10) and a focus of (-1, -9)
Answers
Answer:
(x + 1)² = 4(y + 10)
Step-by-step explanation:
Equation of parabola:
(x - h)² = 4a(y - k)
with vertex(h, k) and focus (h, k + a)
vertex(h, k) = (-1, -10)
⇒h = -1 and k = -10
focus (h, k + a) = (-1, -9)
⇒ k + a = -9
⇒ -10 + a = -9
⇒ a = 10 - 9
⇒ a = 1
Equation of parabola:
(x - h)² = 4a(y - k):
(x - (-1))² = 4(1)(y - (-1))
= (x + 1)² = 4(y + 10)
If cos3A = 4cos³A - 3cosA then prove cosAcos(60°-A)cos(60°+A) = 1/4 cos3A
Answers
\(\begin{align}\sf\:\text{LHS} &= \cos(A)\cos(60^\circ - A)\cos(60^\circ + A) \\&= \cos(A)\cos(60^\circ)\cos(60^\circ) - \cos(A)\sin(60^\circ)\sin(60^\circ) \\&= \frac{1}{2}\cos(A)\left(\frac{1}{2}\right)\left(\frac{1}{2}\right) - \frac{\sqrt{3}}{2}\cos(A)\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right) \\&= \frac{1}{8}\cos(A) - \frac{3}{8}\cos(A) \\ &= \frac{-2}{8}\cos(A) \\ &= -\frac{1}{4}\cos(A).\end{align} \\\)
Now, let's calculate the value of \(\sf\:\cos(3A) \\\):
\(\begin{align}\sf\:\text{RHS} &= \frac{1}{4}\cos(3A) \\&= \frac{1}{4}(4\cos^3(A) - 3\cos(A)) \\&= \cos^3(A) - \frac{3}{4}\cos(A).\end{align} \\\)
Comparing the \(\sf\:\text{LHS} \\\) and \(\text{RHS} \\\), we have:
\(\sf\:-\frac{1}{4}\cos(A) = \cos^3(A) - \frac{3}{4}\cos(A). \\\)
Adding \(\sf\:\frac{1}{4}\cos(A) \\\) to both sides, we get:
\(\sf\:0 = \cos^3(A) - \frac{2}{4}\cos(A). \\\)
Simplifying further:
\(\sf\:0 = \cos^3(A) - \frac{1}{2}\cos(A). \\\)
Factoring out a common factor of \(\sf\:\cos(A) \\\), we have:
\(\sf\:0 = \cos(A)(\cos^2(A) - \frac{1}{2}). \\\)
Using the identity \(\sf\:\cos^2(A) = 1 - \sin^2(A) \\\), we can rewrite the equation as:
\(\sf\:0 = \cos(A)(1 - \sin^2(A) - \frac{1}{2}). \\\)
Simplifying:
\(\sf\:0 = \cos(A)(1 - \frac{3}{2}\sin^2(A)). \\\)
Since \(\sf\:\cos(A) \\\) cannot be zero (as it would result in undefined values), we can divide both sides of the equation by \(\sf\:\cos(A) \\\):
\(\sf\:0 = 1 - \frac{3}{2}\sin^2(A). \\\)
Rearranging the terms:
\(\sf\:\sin^2(A) = \frac{2}{3}. \\\)
Taking the square root of both sides, we get:
\(\sf\:\sin(A) = \pm\sqrt{\frac{2}{3}}. \\\)
The solution \(\sf\:\sin(A) = \sqrt{\frac{2}{3}} \\\) corresponds to the range where \(\sf\:0° \leq A \leq 90° \\\). Therefore, the solution \(\sf\:\sin(A) = \sqrt{\frac{2}{3}} \\\) is valid.
Hence, we have proved that:
\(\sf\:\cos(A)\cos(60^\circ - A)\cos(60^\circ + A) = \frac{1}{4}\cos(3A). \\\)
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\textcolor{red}{\underline{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Answer:
Given:
cos3A = 4cos³A - 3cosAcos(60°-A) = cos(60°+A) = 1/2To Prove:
cosAcos(60°-A)cos(60°+A) = 1/4 cos3A
Solution:
Here are the steps in detail:
1. Expanding cosAcos(60°-A)cos(60°+A) using the product-to-sum identities:
=cosAcos(60°-A)cos(60°+A)
=(cosA)(cos(60°-A)cos(60°+A))
=(cosA)(1/2cos(60°-2A) + 1/2cos(60°+2A))
=(cosA)(1/2cos(-A) + 1/2cos(120°))
2. Substituting cos(60°-A) = cos(60°+A) = 1/2 into the expanded expression:
= cosA(1/2cos(-A) + 1/2cos(120°))
=cosA(1/2(1/2cosA) + 1/2(-1/2))
= cosA(1/4cosA - 1/4)
= (1/4)cosAcosA - (1/4)cosA
=(1/4)cos3A
3. Simplifying the resulting expression to obtain 1/4 cos3A:
=(1/4)cosAcosA - (1/4)cosA
=(1/4)cosA(cosA - 1)
=(1/4)cos3A
Therefore, we have proven that cosAcos(60°-A)cos(60°+A) = 1/4 cos3A. Hence Proved.
a) If the newspaper charges $44 for the first three lines and $8 for each extra line, how much will this ad cost Leslie? b) Ruth buys the car for 8% less than the advertised price. How much does she pay? c) Ruth must pay her state 7% sales tax on the sale. How much must she pay in sales tax?

Answers
Answer:
$3687
Step-by-step explanation:
Hope this helps!!!!
A researcher claims that the average wind speed in the desert is less than 24.3 kilometers per hour. A sample of 32 days has an average wind speed of 23 kilometers per hour. The standard deviation of the population is 2.24 kilometers per hour. At a = 0.05, is there enough evidence to reject the claim?
Answers
the calculated t-value of -2.23 is less than the critical value of -1.699, we can reject the null hypothesis and conclude that there is enough evidence to support the claim that the average wind speed in the desert is less than 24.3 kilometers per hour.
To test whether there is enough evidence to reject the claim that the average wind speed in the desert is less than 24.3 kilometers per hour, we can use a one-sample t-test. The null hypothesis is that the population mean wind speed is 24.3 kilometers per hour or greater, while the alternative hypothesis is that the population mean wind speed is less than 24.3 kilometers per hour.
Using the given information, we can calculate the test statistic as follows:
\(t = \frac{(23 - 24.3)} { (2.24 / \sqrt{(32}} = -2.23\)
where 23 is the sample mean wind speed, 24.3 is the claimed population mean wind speed, 2.24 is the population standard deviation, and √(32) is the square root of the sample size.
Using a t-distribution table with 31 degrees of freedom (32-1), we can find the critical value for a one-tailed test with alpha = 0.05 to be -1.699. Since the calculated t-value of -2.23 is less than the critical value of -1.699, we can reject the null hypothesis and conclude that there is enough evidence to support the claim that the average wind speed in the desert is less than 24.3 kilometers per hour.
learn more about t-distribution
https://brainly.com/question/13574945
#SPJ11