May you please Simplify 15/365? If you can't it's okay. If you can Thank you
Answers
The fraction 15/365 has been simplified as 3/73.
In the fraction 15/365, the numerator is 15, and the denominator is 365. The numerator represents the number of parts we're interested in, and the denominator represents the total number of parts in the group. So, in this case, we're interested in 15 parts out of a group of 365.
To simplify this fraction, we need to find a common factor of the numerator and the denominator that we can divide both by. In this case, 5 is a common factor of both 15 and 365. Dividing both by 5 gives us:
15/365 = (15 ÷ 5) / (365 ÷ 5) = 3/73
To know more about fraction here
https://brainly.com/question/10354322
#SPJ4
Related Questions
Probability Distributions for Discrete Random Variables
Which of the following are discrete random variables?
Select all that apply
1-The number of CDs that a college student owns
2- The number of dogs you own
3- The amount of gas in your car
4- Number of 6s you get when you throw 5 number cubes
5- The number of dog sleds that a competitor uses in an annual sled dog race

Answers
The discrete random variables from the given options are: 1, 2, 4, and 5.
The number of CDs that a college student owns: This is a discrete random variable because the number of CDs can only be a whole number. You cannot have a fractional or continuous value for the number of CDs.
The number of dogs you own: This is a discrete random variable because you can only own a whole number of dogs. You cannot own a fractional or continuous number of dogs.
Number of 6s you get when you throw 5 number cubes: This is a discrete random variable because the number of 6s can only be a whole number from 0 to 5. You cannot have a fractional or continuous value for the number of 6s obtained.
The number of dog sleds that a competitor uses in an annual sled dog race: This is a discrete random variable because the number of dog sleds can only be a whole number. You cannot have a fractional or continuous value for the number of dog sleds used.
On the other hand, the following option is not a discrete random variable:
The amount of gas in your car: This is a continuous random variable because the amount of gas can be any non-negative real number. It can have fractional or continuous values, such as 10.5 liters or 20.25 gallons. Option 1,2,3,4 and 5
For more such questions on random variables visit:
https://brainly.com/question/17217746
#SPJ11
who is the Malala yousafzai?
Answers
Answer:
pakistani activist for female education
Find the surface area of the right triangular prism (above) using its net (below).

Answers
Answer:
The Answer is 96 units squared
Step-by-step explanation:
First, you find the area of all the sides:
Triangle 1: 6
Triangle 2: 6
Rectangle 1: 21
Rectangle 2: 28
Rectangle 3: 35
Then you add all of the numbers together.
6+6+21+28+35 = 96 units squared
I hope this helps :)
Circles Test
Assume that lines that appear tangent are tangent. Find the value of the variables,
208
A. a = 40; b=130; c = 70
B. a = 36; b=140; c = 70
Ca = 20; b=160; C = 90
D. a = 40; b=140; c = 90

Answers
Answer:
\(D. a = 40; b=140; c = 90\)
Step-by-step explanation:
\(a=2(20)\\\\=40\)
---------------
\(b=180-40\\\\=140\)
---------------
\(c=90\)
--------------------------
hope it helps...
have a great day!!
For fixed population standard deviation and level of significance, the minimum sample size needed to guarantee a given margin of error ___________- as the margin of error increases.
Answers
For fixed population standard deviation and level of significance, the minimum sample size needed to guarantee a given margin of error decreases as the margin of error increases.
The square root of the variance for the given set of numbers is what the standard deviation examines. It is employed to compute a confidence interval for making judgments (such as accepting or rejecting a hypothesis).
Here, the population standard deviation, and level of significance are the same.
As the margin of error increased.
So, with the increase in the value of the margin of error, there will surely decrease in the value of the sample size
\($$\begin{aligned}&\mathrm{MOE}_\gamma=z_\gamma \times \sqrt{\frac{\sigma^2}{n}}\\&\begin{aligned}\mathrm{MOE} & =\text { margin of error } \\\gamma & =\text { confidence level } \\z_\gamma & =\text { quantile } \\\sigma & =\text { standard deviation } \\n & =\text { sample size }\end{aligned}\end{aligned}$$\)
As the margin of error is in the denominator position in the sample size formula
Hence with an increase in the margin of error sample size decreases.
For more question on margin of error
https://brainly.com/question/24289590
#SPJ4
What is the term that relates to the way data tend to cluster around some middle or central value.
Answers
Central tendency, is the term that relates to the way data tend to cluster around some middle or central value.
Measures of central tendency are summary statistics that represent the center point or typical value of a dataset. Examples of these measures include the mean, median, and mode. These statistics indicate where most values in a distribution. Mode in statistics is the number of times a number is repeated. The number which is repeated maximum times in a series of data is known as the modular number. The mode is used to compare data that has extreme figures. Central tendency simply means most scores in a normally distributed set of data tend to cluster near the center of a distribution.
To learn more about Central tendency, refer:
https://brainly.com/question/1288901
#SPJ4
Which expression has a term with a coefficient greater than 1?

Answers
Answer:
1/2+3y
Step-by-step explanation:
a coefficient is the number in front of the variable.
Hope this helps
Answer:
1/2+3y
Step-by-step explanation:
The expression 3/4y+5 has a coefficient of 3/4, so it's not greater than 1
The expression 4+y has a coefficient of 1, so it's not greater than 1
The expression 1/2+3y has a coefficient of 3, so it's greater than 1
The expression y-4*1 has a coefficient of 1, so it's not greater than 1
Hannah has a kitten that weighs 2 pounds. When her kitten is grown, the vet said that it would weigh 17 pounds. How many more ounces will the kitten weigh when it is a grown cat?
Answers
Robert's monthly bank statement showed the following deposits and withdrawals: -−$113.24, $98.07, -−$18.74, -−$98.17, $37.13 If Robert's balance in the account was $110.31 at the beginning of the month, what was the account balance at the end of the month? Answer: \$$
Answers
Answer:
The correct answer is −94.95
Organisms A and B start out with the same population size.
Organism A's population doubles every day. After 5 days, the population stops growing and a virus cuts it in half every day for 3 days.
Organism B's population grows at the same rate but is not infected with the virus. After 8 days, how much larger is organism B's population than organism A's population? Answer the questions to find out.
1. Use your answers to questions 3 and 4 to write an expression for how many times greater organism B's population is than organism A's population after 8 days.
Simplify your expression, then write it as a number that is not in exponential form. Show your process.
Answers
The expression is y = 64x
Where x is the population of organism A.
y is the population of organism B.
What is an expression?
An expression contains one or more terms with addition, subtraction, multiplication, and division.
We always combine the like terms in an expression when we simplify.
We also keep all the like terms on one side of the expression if we are dealing with two sides of an expression.
Example:
1 + 3x + 4y = 7 is an expression.
3 + 4 is an expression.
2 x 4 + 6 x 7 – 9 is an expression.
33 + 77 – 88 is an expression.
We have,
Organism A.
The population size after 5 days.
= \(2^5\)
= 32
And,
The virus cuts the population in half for 3 days.
So,
The population size after 8 days.
= \(\frac{32}{2^3}\)
= \(\frac{32}{8}\)
= 4
Organism B.
The population size after 8 days.
= \(2^8\)
= 256
Now,
The relationship of the population of organisms A and B after 8 days.
= 4 x Population of organism A
= 4 x 64
= 256
= Population of organism B
We can write as an expression.
y = 64x
Where x is the population of organism A.
y is the population of organism B.
Thus,
Organism B's population is 64 times larger than organism A's population after 8 days.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ9
Find the area under the standard normal curve to the left of z=2.06. round your answer to four decimal places.
Answers
The area under the standard normal curve to the left of z = 2.06 is approximately 0.9803.
The normal distribution function, also known as the Gaussian distribution or bell curve, is a probability distribution that is symmetric, bell-shaped, and continuous. It is defined by two parameters: the mean (μ) and the standard deviation (σ).
The normal distribution is widely used in statistics and probability theory due to its many desirable properties and its applicability to various natural phenomena. It serves as a fundamental distribution for many statistical methods, hypothesis testing, confidence intervals, and modeling real-world phenomena.
To find the area under the standard normal curve to the left of z = 2.06, you can use a standard normal distribution table or a calculator with a normal distribution function. The standard normal distribution is a normal distribution with a mean of 0 and a standard deviation of 1.
Using a standard normal distribution table, the area to the left of z = 2.06 can be found by looking up the corresponding value in the table. However, since the standard normal distribution table typically provides values for z-scores up to 3.49, we can approximate the area using the available values.
The closest value in the standard normal distribution table to 2.06 is 2.05. The corresponding area to the left of z = 2.05 is 0.9798. This means that approximately 97.98% of the area under the standard normal curve lies to the left of z = 2.05.
Since z = 2.06 is slightly larger than 2.05, the area to the left of z = 2.06 will be slightly larger than 0.9798.
Therefore, rounding the answer to four decimal places, the area under the standard normal curve to the left of z = 2.06 is approximately 0.9803.
To know more about function visit:
https://brainly.com/question/31062578
#SPJ11
Given the functions f(x) and g(x + 2) - 4, what translation(s) to the graph of f(x) is (are) done so that the graph of g(x) is obtained from the graph of f(x)?
Answers
Answer:
my mom calls me I'll be back
Dan made $5.38 for a half hour of work. At Dan's current rate of pay, how much would Dan make for 8 hours of work?
WILL RECIEVE ANYTHING YOU WOULD LIKE
Answers
Answer:
107.6
Step-by-step explanation:
5.38 is how much is made in half an hour so I multiplied that by 2 to get the complete hour then multiplied that by 8
Answer: I am pretty sure it’s 87.08
Step-by-step explanation:
Can someone help me solve this?

Answers
The function is an exponential growth since it is increasing with time and k is positive
What is exponential growth?
Given that at t =6, P = 167075
Then;
167075 =110.8e^6k
167075/110.8 = e^6k
1507.9 = e^6k
ln(1507.9) = 6k
k = ln(1507.9)/6
k = 1.2
Thus in the year 2020;
P = 110.8e^20(1.2)
P = 2.9 * 10^12
In the year 2025;
P = 110.8e^25(1.2)
P = 1.18 * 10^15
To reach 290,000
290,000 = 110.8e^1.2t
290000/110.8 = e^1.2t
2617.3 = e^1.2t
t = ln(2617.3 )/1.2
t = 7 years
Learn more about exponential:https://brainly.com/question/28596571
#SPJ1
Write each number in scientific notation.
160,000,000
29,830
0.000350
Please answer asap!!
Thank you
Answers
Answer:
one hundred sixty million, twenty-nine thousand eight hundred thirty, thirty-five hundred thousandths
Step-by-step explanation:
Each of the numbers written in word form instead of standard form. Hope it helps!
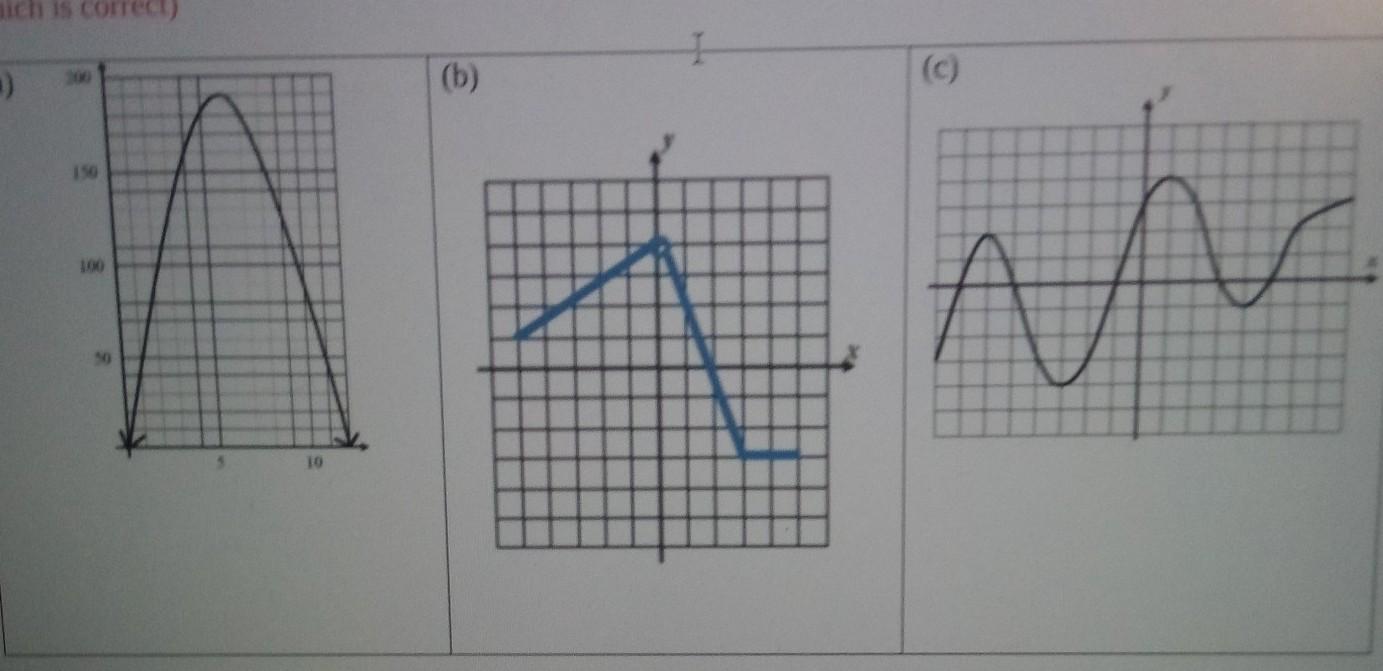
determine the domain and range of each function below from its graph:
Answers
Problem
Solution
Part a
For this case we can see that the domain is given by:
Domain
0<= x <= 12
Range
0<= y<=190
Part b
Domain
-5<=x<0 U 0Range
-3<=y<=4
Part c
Domain
-8 <= x<= 8
Range
-4 <= y<= 4

a pencil that is 4 in. long (starting at x=2) and has a density function of rho(x)=5/x oz/in.
Answers
The mass of the pencil is approximately 5.49 ounces.
To find the mass of the pencil, we can integrate the density function over the length of the pencil.
The density function is given by rho(x) = 5/x oz/in.
We want to find the mass of the pencil, so we integrate the density function from x = 2 (the starting point of the pencil) to x = 6 (the endpoint of the pencil).
The integral is ∫[2, 6] (5/x) dx.
Evaluating the integral, we have:
∫[2, 6] (5/x) dx = 5 ln(x) ∣[2, 6] = 5 ln(6) - 5 ln(2) = 5 (ln(6) - ln(2)).
Using the property of logarithms, we can simplify this to:
5 ln(6/2) = 5 ln(3) ≈ 5 (1.098) ≈ 5.49 oz.
The mass of the pencil is approximately 5.49 ounces.
For more such questions on mass
https://brainly.com/question/28916233
#SPJ8
Collen can paint a room in 12 hours. Rebecca can paint the same room in 20 hours. How long does it take for both Collen and Rebecca to paint the room if they are working together
Answers
To solve the problem, we need to use the concept of work done. The work done in the problem is the painting of the room. We know that the time taken by Collen to paint the room is 12 hours. The time taken by Rebecca to paint the same room is 20 hours.
Let x be the time taken by both of them working together to paint the same room. The formula used to solve this problem is based on the concept of work done. Work done = Rate x TimeTo solve the problem, we need to follow these steps;Step 1: Calculate the work rate for Collen and Rebecca. We know that Collen can paint the room in 12 hours. Therefore, his rate is 1/12. Rebecca can paint the same room in 20 hours. Therefore, her rate is 1/20. Step 2: Find the rate of work done by both of them working together.
We can find this rate by adding the individual rates. That is, 1/12 + 1/20 = 2/60 + 3/60 = 5/60 or 1/12. Thus, the rate of work done by both of them working together is 1/12. Step 3: Find the time taken for both of them to paint the room working together. We know that the work done is the same. That is, the room has to be painted completely. Therefore, the work done is 1. We can find the time taken by both of them to complete the work by using the formula Work done = Rate x Time. Therefore, 1 = 1/12 x T or T = 12. Thus, it will take 12 hours for both Collen and Rebecca to paint the room if they are working together. Therefore, the final answer is 12 hours.
To know more about work visit :
https://brainly.com/question/18094932
#SPJ11
You are required to: a.Rewrite the formulation above in the standard form by adding the required variables to replace the inequalities. b.Find a solution for the above formulation utilizing the linear programming simplex method.
Answers
Using the simplex method, the optimal solution for the given linear programming problem is x = 2, y = 2, z = 0, with the maximum objective value of P = 10.
a. To rewrite the formulation in standard form, we need to replace the inequalities with equality constraints and introduce non-negative variables. Let's assume x, y, and z as the non-negative variables:
Maximize P = 3x + 2y + 4z
Subject to:2x + y + z + s1 = 8
x + 2y + 3z + s2 = 10
x, y, z ≥ 0
b. Utilizing the linear programming simplex method, we can solve the above formulation. After setting up the initial tableau, we perform iterations by selecting a pivot element and applying the simplex algorithm until an optimal solution is reached. The algorithm involves row operations to pivot the tableau until all coefficients in the objective row are non-negative. This ensures the optimality condition is satisfied, and the maximum value of P is obtained.
To provide a brief solution within 120 words, we determine the optimal solution by applying the simplex method to the above formulation. After performing the necessary iterations, we find that the maximum value of P occurs when x = 2, y = 2, z = 0, with P = 10. Therefore, the maximum value of P is 10, and the solution for the given problem is x = 2, y = 2, and z = 0.
To learn more about simplex method click here
brainly.com/question/32298193
#SPJ11
Let S = {i : 1 < i < 30). In a certain lottery, a subset L of S consisting of six numbers is selected at random. These are the numbers on a winning lottery ticket. (a) What is the probability of winning this lottery by purchasing a lottery ticket that contains the same six integers that belong to L? (b) What is the probability that none of the six integers on your lottery ticket belong to L? (c) Determine the probability that exactly one of the six integers on your lottery ticket belongs to L. Show transcribed image text
Answers
The probability of winning this lottery by purchasing a lottery ticket that contains the same six integers is 0.000002.
The probability that none of the six integers on your lottery ticket belong to L 0.2125.
Total probability that exactly one of the six integers on your lottery ticket belongs to L is 1.4876.
The total number of ways to select a subset of 6 numbers from the set S of 29 numbers is given by,
The binomial coefficient C(29,6).
The number of ways to select the 6 numbers that match the winning lottery numbers is 1.
The probability of winning the lottery is,
P(winning)
= 1/C(29,6)
= 1/475020
=0.000002
The number of ways to select a subset of 6 numbers from the remaining 23 numbers (not in L) is given by,
The binomial coefficient C(23,6).
The probability that none of the 6 numbers on your lottery ticket belong to L is,
P(none of the 6 on ticket belong to L)
= C(23,6) / C(29,6)
=100947/475020
=0.2125
To compute the probability that exactly one of the 6 integers on your lottery ticket belongs to L, consider two cases,
The winning lottery ticket has exactly one number that is also on your ticket.
There are C(6,1) ways to choose the common number.
And C(23,5) ways to choose the remaining 5 numbers on the winning ticket from the remaining 23 numbers.
The probability is,
P(one match)
= C(6,1) × C(23,5) / C(29,6)
= 6 × 0.2125
=1.275
The winning lottery ticket has no numbers that are on your ticket.
There are C(23,6) ways to choose the 6 numbers on the winning ticket from the remaining 23 numbers.
The probability is,
P(zero matches)
= C(23,6) / C(29,6)
= 0.2125
The total probability of exactly one match is,
P(exactly one match)
= P(one match) + P(zero matches)
=1.275 + 0.2125
= 1.4876
learn more about probability here
brainly.com/question/13103111
#SPJ4
The given scenario involves randomly selecting a subset of six integers from a set of 28 integers. The probability of winning the lottery by purchasing a ticket containing the same six integers as the winning ticket is simply the probability of selecting those six integers out of the 28.
This can be calculated as 6/28 x 5/27 x 4/26 x 3/25 x 2/24 x 1/23 = 0.000018. The probability that none of the six integers on your lottery ticket belong to L is the complement of the probability of winning the lottery, which is 1 - 0.000018 = 0.999982.
(a) To find the probability of winning, we need to determine the number of possible subsets of size 6 from S (which has 28 integers). The number of combinations is C(28,6). Since there's only 1 winning subset, the probability of winning is 1/C(28,6).
(b) To find the probability that none of the 6 integers on your ticket belong to L, you need to select 6 numbers from the remaining 22 integers in S (excluding the winning numbers). The number of combinations is C(22,6). So, the probability is C(22,6)/C(28,6).
(c) To find the probability that exactly one integer on your ticket belongs to L, you need to select 1 winning number (C(6,1)) and 5 non-winning numbers (C(22,5)). The total combinations are C(6,1)*C(22,5). The probability is [C(6,1)*C(22,5)]/C(28,6).
Learn more about randomly here: brainly.com/question/31980274
#SPJ11
Jacob spent $40 dollars on supplies to make 100 shirts for a baseball team fundraiser. Solve the inequality to help him decide how much to charge for each shirt to make a profit of more than $350
100t - 40 > 350
A) t < 39
B) t < 31
C) t > 39
D) t > 31
Answers
Answer:
I do believe the answer is A
2x+14= -21-5x
Need to find out what x is but a step by step explanation please
Answers
2x+14=-21-5
I am choosing that all constants will be on the right side, so I will do the inverse operation of any constant on the left side to remove it. Here, a constant on the left side is 14. I will subtract 14 from both sides of the equation. Positive 14 minus 14 is zero, so it cancels out and removes it.
2x+14-14 = -21-5x
2x = -35-5x
See how the 14 is now gone? The equation looks much simpler now. Okay next, you can see that there is a coefficient on the “constant side” that I’ve chosen, so I am going to remove that. Negative 5 plus positive 5 equals zero. Do this on both sides of the equation.
2x+5x = -35-5x+5x
7x = -35
Now the equation is just two numbers. All that is left to do is divide by the last coefficient, 7, in this case.
7x/7 = -35/7
x = -5
Answer:
Step-by-step explanation:
solve for x
2x+14=-21-5
2x+14=-26
subtract 14 from both sides
2x+(14-14)=-14-26
2x=-14-26
2x=-40
divide both sides of 2x = -40 by 2
\(\frac{2x}{2} =\frac{-40}{2}\)
2/2=1
x=\(\frac{-40}{2}\)
x= -20
Explain how to solve this problem:
A credit card company charges 12.9% annual interest. If they
compound interest monthly, how much will you owe for every dollar
you do not pay off for a year?
Answers
"every dollar" means P = 1
compounded monthly interest means 12
1(1+(.129/12)^(12(1)) =
in calculator do pemdas
1. .129/12 = 0.01075
2. 0.01075 + 1 = 1.01075
3. (1.01075)^12 = 1.136907156 =
answer = 1.14
Mayfield schools
lcps
what is the slope intercept for
(5,1) and (2,16)
Answers
So the slope-intercept form of the equation of the line passing through the two given points is:
y = -5x + 26
What distinguishes a linear equation?If an equation is expressed in the form y=mx+b, where m denotes the slope and b the y-intercept, it is said to be linear.
The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept.
To find the slope of the line passing through the two given points (5,1) and (2,16), we can use the formula:
m = (y2 - y1)/(x2 - x1)
where (x1, y1) = (5,1) and (x2, y2) = (2,16)
m = (16 - 1)/(2 - 5) = -5
So the slope of the line is -5.
To find the y-intercept b, we can use the point-slope form of the equation of a line:
y - y1 = m(x - x1)
Using the point (5,1) and the slope m = -5, we get:
y - 1 = -5(x - 5)
Simplifying this equation, we get:
y = -5x + 26
So the slope-intercept form of the equation of the line passing through the two given points is:
y = -5x + 26
To know more about linear equation visit:
https://brainly.com/question/29739212
#SPJ1
Assuming all conditions for inference are met, what defines a 95 percent confidence interval for the slope of the least-squares regression line?
Answers
Assuming all conditions for inference are met, a 95 per cent confidence interval for the slope of the least-squares regression line is defined as the range of values within which we are 95 per cent confident that the true population slope lies.
It is calculated as the point estimate (the slope of the least-squares regression line) plus or minus the margin of error, which is determined by multiplying the standard error of the slope by the critical value from the t-distribution with n-2 degrees of freedom (where n is the sample size). This critical value is chosen such that 95 per cent of the t-distribution falls within the interval. Therefore, a larger sample size or a smaller standard error will result in a narrower confidence interval, while a smaller sample size or a larger standard error will result in a wider confidence interval.
Learn more about t-distribution here:
https://brainly.com/question/13574945
#SPJ11
Find the equation of a line that is parallel to y = 5x + 1 and passes through the point (3, -4).
Give your answer in the form y = mx + b.
Answers
Given:
The equation of a line is:
\(y=5x+1\)
A line is parallel to the given line and passes through the point (3,-4).
To find:
The equation of the line in the slope intercept form.
Solution:
The slope intercept form of a line is:
\(y=mx+b\) ...(i)
Where, m is the slope and b is the y-intercept of the line.
We have,
\(y=5x+1\) ...(ii)
On comparing (i) and (ii), we get
\(m=5\)
Slope of the given line is 5.
We know that the slopes of parallel lines are equal. So, the slope of the required line is 5.
The required line passes through the point (3,-4) with slope 5. So, the equation of the required line is:
\(y-y_1=m(x-x_1)\)
\(y-(-4)=5(x-3)\)
\(y+4=5(x)+5(-3)\)
\(y+4=5x-15\)
Subtracting 4 from both sides, we get
\(y+4-4=5x-15-4\)
\(y=5x-19\)
Therefore, the equation of the required line is \(y=5x-19\).
Please please help please please help me please please help now please

Answers
Answer:
A) -0.6
B) 0.5
Step-by-step explanation:
slope=(2--1)÷(9-3)
A binomial probability experiment is conducted with the given parameters. Compute the probability of x successes in the n independent trials of the experiment.
nequals=7
pequals=0.65 xequals=6
(Do not round until the final answer. Then round to four decimal places as needed.)
Answers
The probability of 6 successes in 7 independent trials with a probability of success 0.65 is 0.3052.
Using the binomial probability formula, the probability of x successes in n independent trials with a probability of success p can be calculated as:
P(x) = (n choose x) * p^x * (1-p)^(n-x)
where "n choose x" represents the number of ways to choose x items from a set of n items, and is calculated as:
(n choose x) = n! / (x! * (n-x)!)
So, for the given parameters nequals=7, pequals=0.65, xequals=6, we have:
P(6) = (7 choose 6) * 0.65^6 * (1-0.65)^(7-6)
= 7 * 0.65^6 * 0.35^1
= 0.3052
Therefore, the probability of 6 successes in 7 independent trials with a probability of success 0.65 is 0.3052.
Visit to know more about Probability :-
brainly.com/question/13604758
#SPJ11
Please check the attached picture, please answer thoroughly!

Answers
The selection depends on individual needs, preferences, and the intended use of the tiny house.
a) To find the amount of space inside each house, we need to calculate the volume for each design.
House on the left:
Volume = length x width x height = 2.5 m x 18 m x 2.8 m = 126 m³
Triangular house:
Volume of a triangular prism = (base area x height) / 2
Base area = (1/2) x base x height = (1/2) x 4 m x 10 m = 20 m²
Volume = (20 m² x 7 m) / 2 = 70 m³
b) When comparing the environmental impacts of each house, several factors need to be considered:
Positive impacts:
1. Material usage: Tiny houses use fewer materials, reducing resource consumption and waste generation.
2. Energy efficiency: Smaller living spaces require less energy for heating, cooling, and lighting, leading to lower energy consumption.
3. Land utilization: Tiny houses can be built on smaller plots of land, preserving green spaces and reducing urban sprawl.
Negative impacts:
1. Construction materials: Although tiny houses use less material overall, the environmental impact depends on the types of materials used. Sustainable and eco-friendly materials should be prioritized.
2. Water and waste management: Adequate provisions for water supply and waste disposal should be implemented to minimize environmental impacts.
3. Transportation: The transportation of tiny houses to their locations can contribute to carbon emissions if not done efficiently.
c) The choice of design for a tiny house depends on personal preferences and priorities. However, considering the provided information:
The house on the left offers a larger interior space of 126 m³, providing more room for living and storage. It may be suitable for individuals or couples who desire more space and functionality within their tiny house.
The triangular house has a smaller interior volume of 70 m³ but offers a unique design and aesthetic appeal. It may be preferred by individuals who prioritize a distinctive architectural style or who are looking for a minimalist and cozy living space.
Ultimately, the selection depends on individual needs, preferences, and the intended use of the tiny house. Factors such as lifestyle, desired amenities, and personal values regarding sustainability and resource conservation should be considered when making the final decision.
for more such question on intended visit
https://brainly.com/question/31252264
#SPJ8
Factor the expression completely 6x^2 + 21x - 12
Answers
Answer:3(2−1)(+4)
Step-by-step explanation:
62+2
1−1
6x^{2}+21x-12
6x2+21x−12
3(22+7x−4)
3(2x^{2}+7x-4)
3(2x2+7x−4)
3(22+7−4)
3(2x2+7x−4)
3(22+8−−4)
3(2x2+8x−x−4)
3(22+8−−4)
3(2x^{2}+8x-x-4)
3(2x2+8x−x−4)
3(2(+4)−1(+4))
3(2x(x+4)-1(x+4))
3(2x(x+4)−1(x+4))
3(2(+4)−1(+4))
3(2x(x+4)-1(x+4))
3(2x(x+4)−1(x+4))
3(2−1)(+4)