Marta used a coupon to save $3.50 on a book she bought. when marta bought the book,she gave the Clark a $20.00 bill,and the coupon.the sales gave Marta $9.01 in change.
Answers
Answer: OMG MY HERO ACADEMIA I LOVE YOUR PROFILE PICTURE!!!!!!!!!
Step-by-step explanation: Thanks for the points!!!! :)



Related Questions
Find the distance between points A = (2, 0) and
B= (0, 9). Round your answer to the nearest tenth.
Show your work
Answers
Answer:
9.2
Step-by-step explanation:
You want the distance between A(2, 0) and B(0, 9).
DistanceThe distance formula is based on the Pythagorean theorem. It tells you the distance between (x1, y1) and (x2, y2) is ...
d = √((x2 -x1)² +(y2 -y1)²)
For the given points, this becomes ...
d = √((0 -2)² +(9 -0)²) = √(4+81) = √85
d ≈ 9.2
The distance between A and B is about 9.2 units.

A stone is dropped from the upper observation deck of a tower, 950 m above the ground. (Assume g = 9.8 m/s2.)
(a) Find the distance (in meters) of the stone above ground level at time t.
h(t) = 13.92
(b) How long does it take the stone to reach the ground? (Round your answer to two decimal places.)
s
(c) With what velocity does it strike the ground? (Round your answer to one decimal place.)
m/s
(d) If the stone is thrown downward with a speed of 6 m/s, how long does it take to reach the ground? (Round your answer to two decimal places.)
s
Answers
a) The distance of the stone above ground level at any time t is given by h(t) = 950 + 4.9t², where h(t) is measured in meters and t is measured in seconds.
b) It takes approximately 13.93 seconds for the stone to reach the ground.
c) The stone strikes the ground with a velocity of approximately 136.04 m/s.
d) It takes approximately 16.75 seconds for the stone thrown downward with a speed of 6 m/s to reach the ground.
When objects are dropped or thrown from a height, their speed and position can be determined using physics equations. In this problem, we will calculate the distance, time, and velocity of a stone dropped from a tower.
First, we need to determine the equation for the height of the stone above the ground at any given time t. We can use the formula:
h(t) = h0 + vt + 0.5at²
where h0 is the initial height, v is the initial velocity (which is zero for a dropped object), a is the acceleration due to gravity (g = 9.8 m/s^2), and t is the time since the stone was dropped.
Using the given values, we can plug in the numbers and simplify:
h(t) = 950 + 0t + 0.5(9.8)t²
h(t) = 950 + 4.9t²
To find the time it takes for the stone to reach the ground, we need to set h(t) = 0 and solve for t:
0 = 950 + 4.9t^2
t^2 = 193.88
t ≈ 13.93 seconds
To find the velocity at which the stone strikes the ground, we can use the formula:
v = v₀ + at
where v₀ is the initial velocity (which is zero for a dropped object) and a is the acceleration due to gravity (g = 9.8 m/s²). We can plug in the values for t and solve for v:
v = 0 + 9.8(13.93)
v ≈ 136.04 m/s
Finally, if the stone is thrown downward with a speed of 6 m/s, we can use the same formula for h(t) as before, but with an initial velocity of -6 m/s. We can then find the time it takes to reach the ground using the same method as before:
h(t) = 950 - 6t + 0.5(9.8)t²
0 = 950 - 6t + 4.9t²
t² - 1.22t - 193.88 = 0
t ≈ 16.75 seconds
To know more about speed here.
https://brainly.com/question/4199102
#SPJ4
Evaluate x/y for x = 3/10 and = 4/5
A: 7/50
B: 7/15
C: 3/8
D: 12/50
Answers
Answer:The correct anserw is B.
Step-by-step explanation:
At 6 A.M. the temperature was -5 degrecs Celsius. In the afternoon, the temperature was 10 degrees Celsius. What was the change of temperature during the day?
Answers
The change in temperature is just the difference of the temperature
\(10-(-5)\text{ = 10+5=15}\)So, the temperature has changed 15 degrees Celsius during the day.
The first sequence rule is multiply by 3 starting from 5. The second sequence rule is add 9 starting from 18. What is the first number that appears in both sequences?
27
45
72
135
what is the answer
Answers
Considering the sequences given, the first number that appears in both sequences is given by: 45.
What numbers appear in the first sequence?The rule is multiply by 3 starting from 5, hence the numbers are:
(5, 15, 45, 135, ...).
What numbers appear in the second sequence?The rule is add 9 starting from 18, hence the numbers are:
(18, 27, 36, 45, ...).
45 is the first number that appeared in both sequences.
More can be learned about sequences at https://brainly.com/question/6561461
#SPJ1
Inequalities - Introduction

Answers
Answer:
Step-by-step explanation:
This number line says that we can take all values of x that are less than or equal to 2. That is, the solution is
\(x\leq 2\)
NOTE: if the circle at 2 were not filled in then that would mean x<2 (2 would not be an accepted value of x)
need help on my final, dealing with parent functions

Answers
Answer:
x = 3 squared and it is the righr answer
Answer:
pretty hard to read. Sorry
Step-by-step explanation:
Graph the line with slope 1/3 and y-intercept −2.
Answers
The graph of the function y = 1/3x - 2 is added as an attachment
Sketching the graph of the functionFrom the question, we have the following parameters that can be used in our computation:
Slope = 1/3y-intercept = -2So, the equation is
y = 1/3x - 2
The above function is a linear function that has been transformed as follows
Vertically stretched by a factor of 1/3Shifted down by 2 unitsNext, we plot the graph using a graphing tool by taking note of the above transformations rules
The graph of the function is added as an attachment
Read more about functions at
brainly.com/question/2456547
#SPJ1

Hi can someone who is great at math please help me with these math questions. I'm struggling with them!!


Answers
The value of x will be 18.67 for the given data of the triangle.
We have,
Thale's theorem:
When a line parallel to one side of a triangle intersects the other two sides in distinct points, the other two sides are divided in the same ratio.
Given that the sides of the triangle are divided into two parts,
For the left part the parts will be x and x + 7 for the right side the parts will be 16 and 22.
The ratio will be the same according to Thale's theorem. The value of x will be calculated as:-
x / ( x + 7 ) = 16 / 22
22x = 16x + 112
6x = 112
x = 112 / 6
x = 18.67
Therefore, the value of x will be 18.67.
To know more about Thale's theorem follow
brainly.com/question/14417137
#SPJ1
complete question;
Find the values of x and y. Find value of x.
Determine the percentage of all samples of three men that have mean brain weights within 0.1 kg of the population mean brain weight of kg.
Answers
This question is incomplete
Complete Question
According to one study, brain weights of men are normally distributed with a mean of 1.40 kg and a standard deviation of 0.11 kg.
Determine the percentage of all samples of three men that have mean brain weights within 0.1 kg of the population mean brain weight of 1.40 kg.
Answer:
88.36%
Step-by-step explanation:
When given random samples, the formula for z score that we use is:
z = (x-μ)/σ/√n
where x is the raw score
μ is the population mean
σ is the population
n is number of random samples
mean = 1.40 kg
Standard deviation = 0.11 kg
n = 3
x = mean brain weights within 0.1 kg of the population mean brain weight of 1.40 kg.
= 0.1kg ± 1.40kg
Hence,
For 1.50kg
z = 1.50 - 1.40/0.11/√3
z = -1.57
Probability value from Z-Table:
P(x = 1.50) = 0.9418
For 1.30kg
z = 1.30 - 1.40/0.11/√3
= -1.57
Probability value from Z-Table
P(x= 1.30) = 0.0582
P(x = 1.50) - P(x= 1.30)
0.9418 - 0.0582
= 0.8836
Converting to percentage,
0.8836 × 100
= 88.36%
HELP PLEASE NEED IT THANKS

Answers
Answer:
<
Step-by-step explanation:
1) Substitute 5 into the question
\(\frac{4(5)}{4}\)\(2(5)-3\)2) Work out the sides
\(\frac{4(5)}{4} =5\)\(2(5)-3=7\)3) Put it into an inequality
5 < 7
Hope this helps, have a great day!
suppose that during a test drive of two cars, one car travels 189 miles on the same time that a second car travels 135 miles. If the speed of the second car is 12 miles per hours faster than the speed of the second car, find the speed of both cars.
Answers
Main Answer: s1=42 mi/hr.
s2=30mi/hr.
Concept and definitions should be there:
Just as distance and displacement have distinctly different meanings (despite their similarities), so do speed and velocity. Speed is a scalar quantity that refers to "how fast an object is moving." Speed can be thought of as the rate at which an object covers distance. A fast-moving object has a high speed and covers a relatively large distance in a short amount of time. Contrast this to a slow-moving object that has a low speed; it covers a relatively small amount of distance in the same amount of time. An object with no movement at all has a zero speed.
Formula:
s = {d}/{t}
s=speed
d=distance traveled
t=time elapsed
Given data:
one car travels 189 miles on the same time that a second car travels 135 miles.
Solving part:
Let t be the amount of time the cars are traveling
s1=189/t and s2 = 135/t
We are told:
s1=s2+12
That is
189/t=135/t+12
Multiple t on both sides
⇒189 = 135+12t
⇒12t = 189-135
⇒12t = 54
⇒t = 4.5
s1 = 189/4.5
s1 = 42
s2 = 135/4.5
s2=30
Final Answer:s1=42 mi/hr.
s2=30mi/hr.
To learn about more about the speed visit:brainly.com/question/3328179 #SPJ9.
A ball is thrown from an initial height of 6 feet with an initial upward velocity of 17 ft's. The ball's height h (in feet) after t seconds is given by the following.h=6+17t-16t^2Find all values of t for which the ball's height is 10 feet.Round your answer(s) to the nearest hundredth(If there is more than one answer, use the "or" button.)
Answers
Given:
The height (h) of the ball after t seconds is given by the relationship:
\(h=6+17t-16t^2\)Solution
We are required to find the values of t for which the ball's height is 10 feet.
We set h = 10 feet and then solve the resulting equation.
\(10=6+17t-16t^2\)We can then solve the equation:
\(\begin{gathered} -16t^2\text{ + 17t + 6 - 10 = 0} \\ -16t^2\text{ + 17t - 4 = 0} \\ \text{Divide through by -1} \\ 16t^2\text{ - 17t + 4 = 0} \\ U\sin g\text{ quadratic formular,} \\ x\text{ = }\frac{-b\text{ }\pm\sqrt[]{b^2-4ac}}{2a} \\ we\text{ have,} \\ t\text{ = 0.71s or 0.35s (nearest hundredth)} \end{gathered}\)Answer: 0.71 sec or 0.35 sec
Can I please get some help I’ve been stuck on this question for a while!

Answers
Using the radius of the Ferris wheel and the angle between the two positions, the time spent on the ride when they're 28 meters above the ground is 12 minutes
How many minutes of the ride are spent higher than 28 meters above the ground?The radius of the Ferris wheel is 30 / 2 = 15 meters.
The highest point on the Ferris wheel is 15 + 4 = 19 meters above the ground.
The time spent higher than 28 meters is the time spent between the 12 o'clock and 8 o'clock positions.
The angle between these two positions is 180 degrees.
The time spent at each position is 10 minutes / 360 degrees * 180 degrees = 6 minutes.
Therefore, the total time spent higher than 28 meters is 6 minutes * 2 = 12 minutes.
Learn more on a Ferris wheel here;
https://brainly.com/question/30524034
#SPJ1
could you help me? I will go over more than 10 points



Answers
Answer:
1. Cube
2. Triangular Prism
3. 73.5
Step-by-step explanation:
for the third question: 12.25 per square, 6 squares. 12.25 times 6 = 73.5
A bag contains 2 black balls, 4 yellow balls and 4 white balls....

Answers
Answer:
b
Step-by-step explanation:
Salma is inviting 10 friends to a party. Each friend wants 6 cookies
and each box has 10 cookies.
How many boxes should Salma get?
Answers
Answer:
salma needs 6boxes of cookies
Answer:
6 boxes
Step-by-step explanation:
if there are the 10 friends and each of them want 6 cookies that would be
10 x 6 =60
and if each box has 10 cookies then
60 ÷ 10 = 6
2x +1 < 5 what would be the inequality for this ?
Answers
Answer: x < 2
Step-by-step explanation:
First subtract 1 on both sides
2x < 4
Then divide both sides by 2
x < 2
Hey there!
2x + 1 < 5
SUBTRACT 1 to BOTH SIDES
2x + 1 - 1 < 5 - 1
SIMPLIFY IT!
2x < 5 - 1
2x < 4
DIVIDE 2 to BOTH SIDES
2x/2 < 4/2
SIMPLIFY IT!
x < 4/2
x < 2
Therefore, your answer is: x < 2
(The graph is down below)
Good luck on your assignment & enjoy your day!
~Amphitrite1040:)

Solve for z in the system of equations.
x + y - z = -5
2x - y + z = 8
x - 4y + 3z = 5
Answers
Answer:
z = 20
Step-by-step explanation:
Elimination Method:We can use the elimination method in a systems of 3 equations, just as we did when we were solving systems of 2 equations. While the method we apply it is the same, we have to apply it multiple times as elimination gets rid of one variable (usually) and since we're dealing with 3 variables, that still leaves us with 2 variables and we need to cancel once more.
Applying Elimination Method:
We want to develop two linear equations, by applying elimination twice to each equation at least once, and then from there we can apply elimination once more.
Since we're solving for "z", we don't want to immediately cancel it out. So let's use the following two equations:
\(x+y-z=-5\\\\x-4y+3z\)
Let's cancel out the "x", by manipulating one equation to be -x. We can do this by multiplying one equation by -1, but remember we have to apply this to both sides of the equation. Let's do it to the top one (you could also do it to the bottom one)
\(-1(x+y-z)=-(-5)\implies -x-y+z=5\)
So now let's add the two equations:
\(\ \ \ (-x-\ y+\ z)=5\\+(\ \ x-4y + 3z) = 5\\ ------------\\ -5y+4z=10\)
Now let's apply the same thing, but to the middle and bottom equation. Since they don't have the same absolute value coefficients (ignoring the sign) we need to multiple one by a value other than just negative one. So let's multiply the bottom equation by -2 so that the bottom will have a -2x which will cancel when adding it to 2x
\(-2(x - 4y + 3z) = -2(5)\\-2x + 8y - 6z = -10\)
Now let's add the equations:
\(\ \ \ (\ \ 2x-y+z)=8\\+(-2x + 8y - 6z)=-10\\\\-----------\\7y - 5z = -2\)
So now we have the two equations:
\(7y-5z=-2\\-5y+4z=10\)
From here we can apply any method we want, from here I'll use substitution. Since we want to get rid of the "y", let's solve for "y" in terms of z, so once we substitute we have no "y" terms left.
\(7y-5z=-2\\7y=5z-2\\y=\frac{5z-2}{7}\)
Now let's plug this into the second two-variable equation we made.
\(-5(\frac{5x-2}{7})+4z=10\\\\\frac{-25x+10}{7}+4z=10\\\\\frac{-25}{7}z+\frac{10}{7} + \frac{28}{7}z = \frac{70}{7}\\\\\frac{-25+28}{7}z = \frac{70-10}{7}\\\\\frac{3}{7}z = \frac{60}{7}\\\\z = \frac{60}{7} * \frac{7}{3}\\\\z = 20\)
Simplify the expression:
2d+11x4
Answers
Answer:
2d+44
Step-by-step explanation:
Multiply all numbers without variables:
11x4=44
Add equations:
2d+44
Hence, the correct answer is 2d+44
Answer:
2d+44
Step-by-step explanation:
Multiply:
11x4=44
Final Equation:
2d+44
Naomi collects sets of data from people in her school.
A: Height in centimeters
B: Length of hand in centimeters
C: Length of foot in centimeters
D: Age in years
Which diagram is the most suitable for B and C?
A: Bar Chart
B: Waffle diagram
C: Pie chart
D: Scatter graph
E: Line graph
Answers
Answer:
the answer is scatter graph
i don't understand how to do percentages please explain

Answers
Answer:
$60.79
Step-by-step explanation:
First take off the 30% from $78.95. That will leave you with $55.265.
Add 6% of $78.95 for sales tax (4.737) to the $55,265 = $60.002
Then add the 1% of $78.95 for local option tax (.7895) to the $60.002.
That gives you $60.7915 - round it to the nearest cent and it gives you
$60.79
Answer: $60.7915
Step-by-step explanation:
think of percents as a portion of something
if Dave has to pay 6% tax on something + 1% tax he will pay 7% tax.
This means he will pay 7% of 78.95.
In multiplication 'of' means multiply.
just use this as a rule so 7% × 78.95 will be the amount of tax he has to pay
0.07 × 78.95 = $5.5265
However, he has a 30% off coupon
so,
30% × 78.95 will give the amount he saves
.3 × 78.95 = $23.685 saved
now lets find the actual amount he saves with his coupon after taxes:
$23.685 - $5.5265 = $18.1585 saved
we can subtract this amount by the price and we will have the amount Dave has to pay for the jeans:
$78.95 - $18.1585 = $60.7915
⇒ $60.7915 is the price Dave pays
rounding we get $60 and 79 cents
QUICK! 40 points. Consider this cone with the diameter measure of 17 inches.
A cone with diameter 17 inches and slant height of 22 inches.
What is the surface area of the cone?
SA = Pir2 + Pirl
A. 204Pi in.2
B. 259.25Pi in.2
C. 446.25Pi in.2
D. 663Pi in.2

Answers
259.25π in² is the surface area of the cone
The surface area of a cone can be calculated using the formula SA = πr² + πrl
where r is the radius and l is the slant height.
Given that the diameter is 17 inches, the radius (r) is half of the diameter, which is 17/2 = 8.5 inches.
The slant height (l) is given as 22 inches.
Substituting these values into the formula:
Surface Area = π(8.5)² + π(8.5)(22)
= 72.25π + 187π
= 259.25π
Therefore, the surface area of the cone is 259.25π in²
To learn more on Three dimensional figure click:
https://brainly.com/question/2400003
#SPJ1
Select all the features of ABC
A - It is a right triangle.
B - It is isosceles.
C - It is equilateral.
D - It’s perimeter is 68 units.
E - It’s area is 8.5 square units.
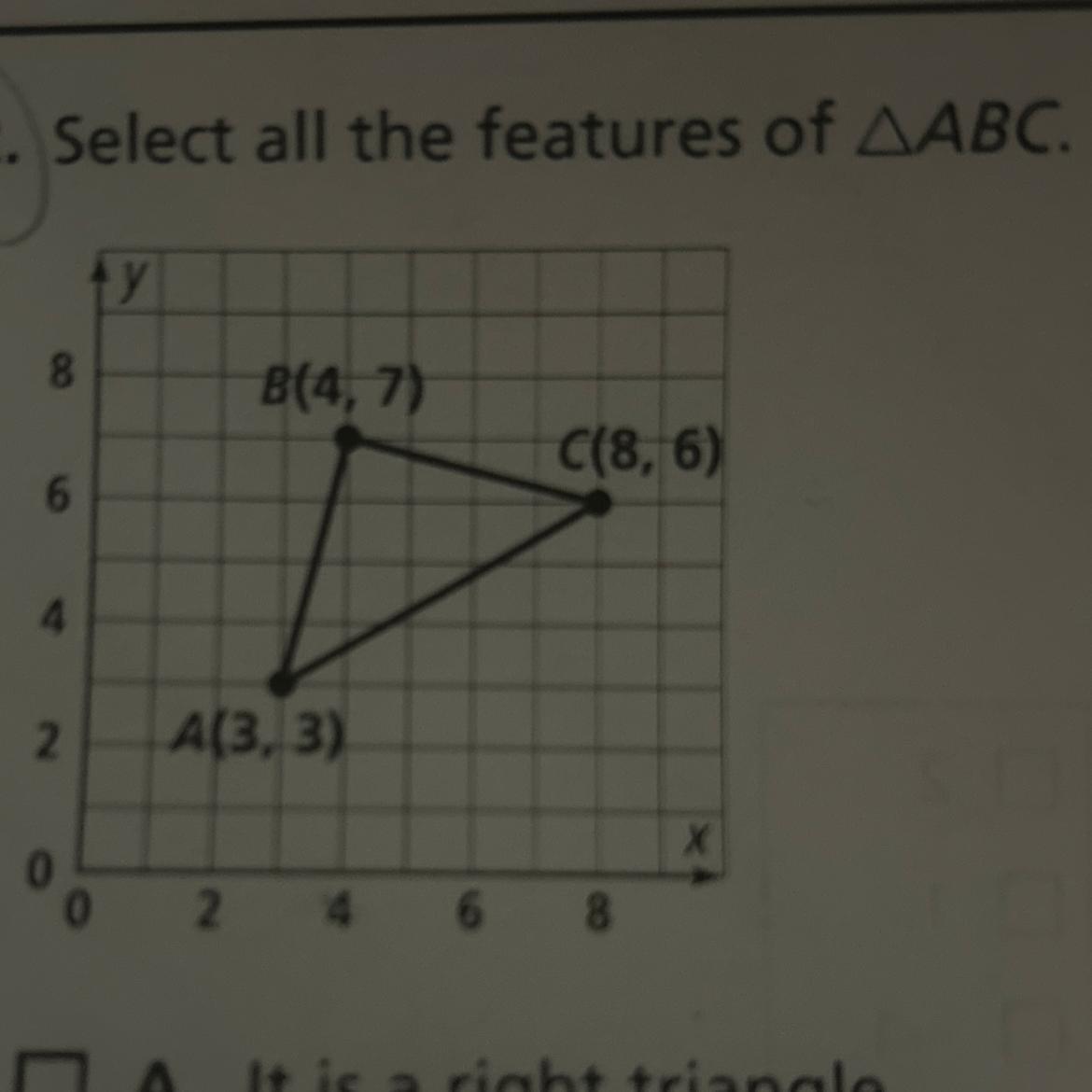
Answers
The features of triangle ABC are:
A - It is a right triangle.B - It is isosceles.D - It’s perimeter is 68 units.How to determine features of a triangle?To check option A, calculate the distance between each pair of points and see if they satisfy the Pythagorean theorem:
AB = \√{(4-3)² + (7-3)²} = \√{41}
BC = \√{(8-4)² + (6-7)²} = \√{17}
AC = \√{(8-3)² + (6-3)²} = 5\√{2}
Now, AB² + BC² = 41 + 17 = AC² is 68 units, which satisfies the Pythagorean theorem and confirms that ABC is a right triangle.
Learn more on triangle features here: https://brainly.com/question/28600396
#SPJ1
Find the scale of the 3 copies
Answers
im sorry but i dont really understand your question :c
what are prime numbers
Answers
Answer:
greater than 1
Step-by-step explanation:
A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers.
Step-by-step explanation:
prime numbers are numbers that have exactly two factors . 1 and the number itself.
use the shell method to find the volume generated by revolving the shaded regions bounded by the curves and lines in exerciss 7-12about the y-axis
Answers
The answer is 1) V = \(2\pi\int\limits(2)+ {x} \, dx\); 2) V = \(2\pi \int\limits(1 - 2x) - 2x dx\); 3) V =\(2\pi \int\limits {\sqrt{2} } \, dx\) ; 4) V = \(2\pi\int\limits {\sqrt{(-2/2)(2-2)} \ dx\) .
1) The volume of the shell is then given by the product of the area of its curved surface and its height. The height is equal to 2 - (-2) = 4, and the radius is equal to the minimum of the distances from x = 2 to the two curves, which is x = 2 - () = 2 + . The volume of the solid is then given by the definite integral:
V = \(2\pi\int\limits(2)+ {x} \, dx\) = \(2\pi [(/3) + 2x]\) evaluated from 0 to 1 = (4/3)π.
2) The height of the region is equal to - (2x) = -2x, and the radius is equal to the minimum of the distances from x = 1 to the two curves, which is x = 1 - (2x) = 1 - 2x. The volume of the solid is then given by:
V = \(2\pi \int\limits(1 - 2x) - 2x dx\)=\(2\pi [/5 - 2/3 + /2]\) evaluated from 0 to 1 = (8π/15).
3) The height of the region is equal to (2-x) - = 2-x. The radius is equal to the minimum of the distances from x = 0 to the two curves, which is x = The volume of the solid is then given by:
V =\(2\pi \int\limits {\sqrt{2} } \, dx\) = \(2\pi [(x^4/4)]\) evaluated from 0 to √2 = (π/2).
4) The height of the region is equal to () - (2-) = 2 - 2. The radius is equal to the minimum of the distances from x = 0 to the two curves, which is x = √((2-)/2). The volume of the solid is then given by:
V = \(2\pi\int\limits {\sqrt{(-2/2)(2-2)} \ dx\) = \(4\pi [(2/3)\± (2\sqrt{2} /3)]\)
The complete Question is:
Use the shell method to find the volumes of the solids generated by revolving the regions bounded by the curves and lines in about the
1. y = x, y = -x/2, and x = 2
2. y = 2x, y = x/2, and x = 1
3. y = x/2, y = 2-x, and x = 0
4. y = 2-x/2, y = x/2, and x = 0
To know more about Shell Methods:
brainly.com/question/17074517
#SPJ4
A college graduate expects to earn a salary of $55,000 during the first year after graduation and receive a 3% raise every year after that. What is the total income he will have received after ten years?
Answers
Answer:
$73915.40
Step-by-step explanation:
→ Find the multiplier
( 3 + 100 ) ÷ 100 = 1.03
→ Multiply by principal amount and raise it to the power of years
55000 × 1.03¹⁰ = 73915.40
Answer: $630,513.36
Step-by-step explanation:
Making a Formula for His Salary on a Given YearLet's make a table of values to see how much he earns every year after graduation.
1 year -> $55,000
2 years -> 55,000 * 103% = $56,650
3 years -> 56,650 * 103% = 55000 * 103% * 103% = $58,349.50
4 years -> 58349.50 * 103% = 55,000 * 103% * 103% * 103% = 55000(1.03)³
Here, we see that every year, he gets 103% of what he got the previous year, which is also 1.03 times his previous salary.
We also see that we multiply 55000 by 1.03 three times in the fourth year, and two times in the third year. This means that we multiply 55000 by 1.03 n-1 times.
Using this, let's generalize this for n.
n years -> \(55000(1.03)^{n-1}\)
Finding the Sum after Ten YearsWe are trying to find his total income after ten years, or the sum of his salary from year 1 to year 10. We can represent this in sigma notation like this
\(% Adjusted limits of summation$\displaystyle\sum_{n=1} ^{10} 55000(1.03)^{n-1}$\)
This essentially translates to the sum of the first ten terms in the sequence \(55000(1.03)^{n-1}\), starting at n=1.
Since this is a geometric sequence, or a sequence where we need to multiply by the same number to get to the next term, we can find the sum using the sum of geometric series formula. This formula is as follows:
\(S_n=a_1\frac{1-r^n}{1-r}\)
where \(S_n\) is the sum of the first n terms, \(a_1\) is the first term, r is the common ratio, and n is the number of terms. In this question, \(S_n\) is the total income after n years, \(a_1\) is his salary after the first year, r is how much his salary increases by each year, and n is the number of years we are calculating the sum for.
\(a_1\) -> 55000
r -> 1.03
n -> 10
Now that we have the values for each variable, let's plug them in and solve
\(S_{10}=55000(\frac{1-1.03^{10}}{1-1.03})\\S_{10}=630513.36\)
The total income he will have received after ten years is $630,513.36.
what is the difference between ANOVA and Z-test Hypothesis
Answers
The difference between ANOVA and Z-test Hypothesis is the Z-test is employed to contrast the averages of single or dual populations, whereas ANOVA is utilized for assessing the means across three or more clusters.
How to determine the differenceThe Z-test becomes possible in the comparison of the mean of a sample to that of the population. It evaluates if there is statistical relevance in the difference between the mean of a sample and the mean of the whole population
In contrast, ANOVA is employed to contrast the averages of three or more separate groups. This assesses if there is a noteworthy distinction in the averages of said groups. The F-statistic in ANOVA is computed by assessing the disparity in variability between groups and the variability within groups.
In a nutshell, the Z-test is employed to contrast the averages of single or dual populations, whereas ANOVA is utilized for assessing the means across three or more clusters.
Learn more about ANOVA at: https://brainly.com/question/25800044
#SPJ1
How would you write this expression as a sum or difference?

Answers
Answer:
A. \(\frac{1}{5} log_3(x) + log_3(y)\)
Step-by-step explanation:
Log rules tell us that multiplication inside a log can be expressed as two summands with the same base.
In other words:
\(\log_c(a*b) =\log_c(a)+\log_c(b)\)
In this case:
\(log_3(\sqrt[5]{x} * y) = log_3(\sqrt[5]{x}) + log_3(y)\)
Using log exponent rules(power can be moved to the front of a log), we get our final answer:
\(\frac{1}{5} log_3(x) + log_3(y)\)