marking braineist!!!
A rectangular prism with a volume of 4 cubic units is filled with cubes with side lengths of 1/3
how many 1/3 fraction unit cubes does it take to fill the prism?
Answers
Answer:
36 cubes
Step-by-step explanation:
Im pretty sure that you have to divide 4 by 1/3*1/3, so 4÷1/9 which is 36 do keep change flip to get 4/1 * 9/1 and multiply 4 by 9 to get 36/1 which is 36. I hope this helps
Sorry Im making an edit to this, i made a mistake, you have ot find the volume of the mini cube, so the volume would be 1/27 not 1/9 (which is the area) so the answer would be 108 sorry again
Related Questions
Why are 4(5) and 20 equivalent expressions?
Answers
Answer:
cos 4 multiplied by 5 gives 20
Step-by-step explanation:
4(5) is the same as 4x5, which equals 20.
helpp meeee i don't understand constant of proportionality (don't put pictures i can't see).

Answers
Answer:
A) 1/5
Step-by-step explanation:
Points on the graph: (10, 2) and (20, 4)
Slope:
m=(y2-y1)/(x2-x1)
m=(4-2)/(20-10)
m= 2/10
m = 1/5
what is The midpoint of G ( -2, -8 ) and H ( -3, -12 )
Answers
Answer:
(-2.5, 10)
Step-by-step explanation:
Which of the following values are in the range of the function graphed below? Check all that apply

Answers
Answer:
B, C, D
Step-by-step explanation:
In this problem, the range is what the output, or y, can be. The origin, or the middie of the graph, is when x=0 and y=0. From the 10s on the screen, we can gather that 5 lines = a distance of 10 on the graph. Using this information, we can say
5 lines = distance of 10
divide both sides by 5 to find the distance for each line
1 line = distance of 2
The function goes from y=0 to three lines down, for a distance of 6. The range is therefore [-6,0] as all values from -6 to 0 on the y axis are included on the graph, including 0 and -6. In this range, -6, -2, and -1 are all included.
In Example 2, suppose Luke couldn't live in his parents' house for free. Instead, no matter whether or not he goes to college, he'd pay $4,800 for housing and spend $2,400 on food. Then, Luke's cost of a year in college would be $ ______.
Answers
Total Cost = $7,200 + E. Let's revisit the question and calculate the cost of Luke's year in college using the provided information.
Given:
- Luke pays $4,800 for housing.
- Luke spends $2,400 on food.
To calculate Luke's cost of a year in college, we need to consider the additional expenses associated with his education. Let's assume the cost of tuition and other educational expenses for one year is represented by the variable "E."
By probability Luke's total cost for a year in college can be calculated as the sum of housing, food, and educational expenses:
Total Cost = Housing Cost + Food Cost + Educational Expenses
Total Cost = $4,800 + $2,400 + E
we cannot determine the exact cost of Luke's year in college. We can only express it as:
Total Cost = $7,200 + E
Learn more about probability here: brainly.com/question/31828911
#SPJ11
complete the following table: (do not round net price equivalent rate and single equivalent discount rate. round the dollar amounts to the nearest cent.)
item list price chain discount net price equivalent rate (in decimals) single equivalent discount rate (in decimals) trade discount net price. LG Blu-Ray player $207 $7/5/3
Answers
Net Price: $177.39
Equivalent Rate: 0.854985
Single Equivalent Discount Rate: 0.145015
Trade Discount: $29.61
Item List Price Chain Discount Net Price Equivalent Rate (in decimals) Single Equivalent Discount Rate (in decimals) Trade Discount Net Price LG Blu-Ray player $207 $7/5/3 $186.30 0.10 0.178 6% $175.36
To find the net price and equivalent rates for the LG Blu-Ray player, we need to apply the chain discount of 7%, 5%, and 3%.
Step 1: Apply the first discount of 7%
$207 * (1 - 0.07) = $207 * 0.93 = $192.51
Step 2: Apply the second discount of 5%
$192.51 * (1 - 0.05) = $192.51 * 0.95 = $182.88
Step 3: Apply the third discount of 3%
$182.88 * (1 - 0.03) = $182.88 * 0.97 = $177.39 (rounded to the nearest cent)
The net price is $177.39.
To find the net price equivalent rate, multiply the discount rates:
0.93 * 0.95 * 0.97 = 0.854985 (in decimals)
To find the single equivalent discount rate, subtract the net price equivalent rate from 1:
1 - 0.854985 = 0.145015 (in decimals)
To find the trade discount, subtract the net price from the list price:
$207 - $177.39 = $29.61
So, the final values are:
Net Price: $177.39
Equivalent Rate: 0.854985
Single Equivalent Discount Rate: 0.145015
Trade Discount: $29.61
Learn more about Equivalent:
brainly.com/question/14672772
#SPJ11
This question has two parts. First, answer Part A. Then, answer Part B. Part A Fill in the blank question. PARKS Rachelle wants to determine the best state park for hiking and fishing. She has developed a metric based on the information she has gathered and the best catch from her previous fishing trips to the parks. Part A Use the metric to calculate a score for each park. Round to the nearest tenth. Park Score = 100[0.2(online rating5)+0.4(miles of trails25)+0.4(fish weight10)] State Park Online Star Rating Hiking Trails (mi) Best Fish (lb) Park Score Gooseberry Falls 4.8 20 9.8 Lake Maria 4.3 14 8.2 Maplewood 4.9 25 7.3 Camden 4.3 15.8 10.1 Part B Part B How might someone who enjoys hiking much more than fishing change this metric? 100 words remaining Tools are not currently accessible
Answers
Answer:
Step-by-step explanation:
Kevin used to run a mile in 9.4
minutes. Now he can run a mile in 8.2
minutes. What is the percent change?
Answers
Answer:
12.77%
Step-by-step explanation:
if a 100% is 9.4
then do
8.2/9.4
which is
0.87234042553
which is
87.23%
then do
100% - 87.23%
which is
12.77%
I NEED Helppp PLEASE!!!

Answers
The given expression \(3 \dfrac{6}{5}\) can be written as \(\sqrt[5]{3^6}\).
What is an expression?Expression in maths is defined as the collection of the numbers variables and functions by using signs like addition, subtraction, multiplication and division.
The given value can be written as:-
\(3\dfrac{6}{5} = \sqrt[5]{3^6}\)
Therefore the given expression \(3 \dfrac{6}{5}\) can be written as \(\sqrt[5]{3^6}\).
To know more about Expression follow
https://brainly.com/question/723406
#SPJ1
3. What is the current price of a common stock that just paid a $4 dividend if it grows 5% annually and investors want a 15% return? (5) ch.7
4(1,05)_4:20 - $42 715-.05 110
4. Redo the preceding problem assuming that the company quits business after 25 years. (5) ch.7
42x 7.05 5. Redo Problem #3 assuming that dividends are constant. (5) 2
Ch.7
=$37,68
4 15 #26.67
6. Redo Problem #3 assuming that dividends are constant and the company quits business after 25 years. (5)
4 x 6.4641 = $25.88
Answers
3. The current price of the common stock is $40.
4. The stock price considering the company quitting business after 25 years is $46.81.
5. The stock price assuming constant dividends is $26.67.
6. The stock price assuming constant dividends and the company quitting business after 25 years is $25.88.
3. The current price of the common stock can be calculated using the dividend discount model. The formula for the stock price is P = D / (r - g), where P is the stock price, D is the dividend, r is the required return, and g is the growth rate. In this case, the dividend is $4, the required return is 15% (0.15), and the growth rate is 5% (0.05). Plugging these values into the formula, we get P = 4 / (0.15 - 0.05) = $40.
4. If the company quits business after 25 years, we need to calculate the present value of the dividends for those 25 years and add it to the final liquidation value. The present value of the dividends can be calculated using the formula PV = D / (r - g) * (1 - (1 + g)^-n), where PV is the present value, D is the dividend, r is the required return, g is the growth rate, and n is the number of years. In this case, D = $4, r = 15% (0.15), g = 5% (0.05), and n = 25. Plugging these values into the formula, we get PV = 4 / (0.15 - 0.05) * (1 - (1 + 0.05)^-25) = $46.81. Adding the final liquidation value, which is the future value of the stock price after 25 years, we get $46.81 + $0 = $46.81.
5. Assuming constant dividends, the stock price can be calculated using the formula P = D / r, where P is the stock price, D is the dividend, and r is the required return. In this case, the dividend is $4 and the required return is 15% (0.15). Plugging these values into the formula, we get P = 4 / 0.15 = $26.67.
6. If the company quits business after 25 years and assuming constant dividends, we need to calculate the present value of the dividends for those 25 years and add it to the final liquidation value. The present value of the dividends can be calculated using the formula PV = D / r * (1 - (1 + r)^-n), where PV is the present value, D is the dividend, r is the required return, and n is the number of years. In this case, D = $4, r = 15% (0.15), and n = 25. Plugging these values into the formula, we get PV = 4 / 0.15 * (1 - (1 + 0.15)^-25) = $25.88. Adding the final liquidation value, which is the future value of the stock price after 25 years, we get $25.88 + $0 = $25.88.
To know more about the dividend discount model, refer here:
https://brainly.com/question/32294678#
#SPJ11
(b) Reasoning Describe a different sequence of steps which you could use to compute the perimeter of the window.
Answers
For regular shapes, add the lengths of the sides, and for irregular shapes, measure each side individually and sum them up. Finally, round the perimeter to the desired level of precision.
To compute the perimeter of a window, here is a different sequence of steps:
1. Identify the shape of the window: Determine if the window has a regular shape, such as a rectangle, square, or circle, or if it has an irregular shape.
2. Measure the sides: If the window is a regular shape, measure the lengths of its sides. For a rectangle or square window, measure the lengths of two adjacent sides. If it's a circular window, measure the radius or diameter.
3. Calculate the perimeter based on the shape:
- For a rectangle or square window: Add the lengths of all four sides together to obtain the perimeter. If the lengths of the adjacent sides are different, ensure you measure each side accurately.
- For a circular window: Calculate the circumference using the formula C = 2πr or C = πd, where r is the radius and d is the diameter of the window. If you have the diameter, divide it by 2 to get the radius.
4. If the window has an irregular shape: In this case, measure each side or segment of the window individually. Then, add up the lengths of all the sides to obtain the total perimeter. Make sure to measure each side accurately, taking into account any angles or curves.
5. Round the perimeter: Once you have calculated the total perimeter of the window, round the value to the desired level of precision or decimal places, depending on your requirements.
It's important to note that accurate measurements are crucial for obtaining an accurate perimeter. Ensure that you use appropriate measuring tools and techniques to obtain precise measurements of the window's sides or segments.
In summary, to compute the perimeter of a window, identify its shape, measure the appropriate sides or segments, and calculate the perimeter based on the shape. For regular shapes, add the lengths of the sides, and for irregular shapes, measure each side individually and sum them up. Finally, round the perimeter to the desired level of precision.
Learn more about perimeter here
https://brainly.com/question/19819849
#SPJ11
is a proper subset different from a regular subset? is an empty set a proper subset? provide an example of a set for your classmates to solve for both a proper subset and an empty set. check and respond to the replies to your examples.
Answers
yes proper subset is different from a regular subset. The empty set is a proper subset of every set except for the empty set
A proper subset of a set A is a subset of A that cannot be equal to A. In other words, if B is a proper subset of A, then all elements of B are in A but A contains at least one element that is not in B.
Subset: If A and B are sets and every element of A is also an element of B, then:
A is a subset of B, denoted by A ⊆ B.
or equivalently, B is a superset of A, denoted by B ⊇ A.
Any set is considered to be a subset of itself. No set is a proper subset of itself. The empty set is a subset of every set. The empty set is a proper subset of every set except for the empty set.
For example, A = {1, 2, 3, 4, 5} and B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
A = {1, 2, 3} and B = {1, 2, 3}
Here, A is a subset of B, or we can say that B is the superset of A.
Proper Subset: If A is a subset of B, but A is not equal to B (that is, there exists at least one element of B which is not an element of A), then
A is also a proper (or strict) subset of B; this is written as A ⊊ B.
For example A = {1, 2, 3} and B = {1, 2, 3, 4}.
Clearly, A is not equal to B and element {4} belongs to set B but is absent in set A, so we have one element in set B which is not an element of set A. Thus, A can be called a proper subset of B.
Hence, a proper subset of a set A is a subset of A that is not equal to A. In other words, if B is a proper subset of A, then all elements of B are in A but A contains at least one element that is not in B, thus the proper subset may or may not be the same.
Learn more about proper subset and empty set here:
https://brainly.com/question/17514113
#SPJ4
do all straight lines that are functions have inverses?
Answers
Answer: Not all Functions have a inverse
Happy To Help :)
Step-by-step explanation:
Need help with this??? Please!!!

Answers
Answer:
the first option
Step-by-step explanation:
(f-g)(x) simply means to subtract both expressions. really literally.
and we go through it power by power of x.
the highest power/exponent of x is 3 (x³). only f(x) has one.
so, -7x³ is the first part of f-g.
next is x².
11x² - 6x² = 5x², which is the second part of f-g.
next is x.
-8x - (-14x) = -8x + 14x = 6x, which is the third part of f-g.
next is x⁰ (in other words, no x, just a constant).
4 - (-3) = 4 + 3 = 7, which is the 4th part of f-g.
we have no x to the power of -1 or -2, so we have -3
0 - (-4x‐³) = 4x‐³, which is the last part of f-g.
so, it is clearly the first answer option.
Which of the following is the last step in problem solving? A. Understand the problem. B. Check your answers and present the solution. C. Come to an answer. OO D. Gather your resources
Answers
Step-by-step explanation:
Come to an answer,I mean final answer after checking all your answers with the solutions.
In an all boys school, the heights of the student body are normally distributed with a mean of 67 inches and a standard deviation of 3.5 inches. Out of the 793 boys who go to that school, how many would be expected to be taller than 6 inches tall, to the nearest whole number?

Answers
Answer:
To determine the number of boys expected to be taller than 6 inches, we need to calculate the proportion of boys taller than 6 inches and then multiply it by the total number of boys in the school.
First, we need to convert the height of 6 inches to a z-score using the formula:
z = (x - μ) / σ
Where:
x = value we want to convert to a z-score (6 inches)
μ = mean of the distribution (67 inches)
σ = standard deviation of the distribution (3.5 inches)
z = (6 - 67) / 3.5 = -61 / 3.5 ≈ -17.43
Next, we can use a standard normal distribution table or a calculator to find the proportion of boys taller than 6 inches, which corresponds to the area under the curve to the right of the z-score -17.43.
Looking up the z-score of -17.43 in a standard normal distribution table, we find that the area to the right of this z-score is essentially 0.
Therefore, we can expect that approximately 0 boys out of the 793 would be taller than 6 inches.
Step-by-step explanation:
Answer:
In an all-boys school, the heights of the student body are normally distributed with a mean of 67 inches and a standard deviation of 3.5 inches. Out of the 793 boys who go to that school, how many would be expected to be taller than 6 inches tall, to the nearest whole number?
To answer this question, we need to find the probability that a randomly selected boy from the school is taller than 6 inches, and then multiply that by the total number of boys in the school. We can use a normal distribution calculator to find the probability.
First, we need to convert 6 inches to the same unit as the mean and standard deviation, which are in inches. 6 inches is equal to 0.5 feet, which is equal to 12/2 = 6 inches. So we are looking for the probability that a boy's height is greater than 6 inches.
Next, we need to find the z-score for 6 inches. The z-score is a measure of how many standard deviations a value is away from the mean. It is calculated by subtracting the mean from the value and dividing by the standard deviation. In this case, the z-score for 6 inches is:
z = (6 - 67) / 3.5
z = -61 / 3.5
z = -17.43
Then, we need to find the probability that a boy's height is greater than 6 inches, which is equivalent to finding the probability that the z-score is greater than -17.43. We can use a normal distribution calculator to find this probability by entering the mean, standard deviation, and z-score values. The calculator will give us the area under the normal curve to the left of the z-score, which is also called the cumulative probability. To find the probability to the right of the z-score, we need to subtract this value from 1.
The normal distribution calculator gives us a cumulative probability of 0 for a z-score of -17.43. This means that almost no boy in the school has a height less than or equal to 6 inches. Therefore, the probability that a boy's height is greater than 6 inches is:
P(height > 6) = 1 - P(height ≤ 6)
P(height > 6) = 1 - 0
P(height > 6) = 1
Finally, we need to multiply this probability by the total number of boys in the school to get the expected number of boys who are taller than 6 inches. This is given by:
E(number of boys > 6) = P(height > 6) × N
E(number of boys > 6) = 1 × 793
E(number of boys > 6) = **793**
Therefore, we can expect **793** boys out of **793** boys in the school to be taller than **6** inches tall, to the nearest whole number.
MARK AS BRAINLIEST!!!
Given rhombus UVWX below. If m/XYU = (10x + 10)°, solve for x.
X
U
W
V

Answers
The value of x if /XYU = (10x + 10)° is 8
How to determine the valueIt is important to note the properties of a Rhombus;
All sides of the rhombus are equalOpposite sides of a rhombus are parallelOpposite angles of are equalDiagonals bisect each other at right anglesDiagonals bisect the anglesThe sum of two adjacent angles is 180 degreesThen, we have that;
m/XYU = (10x + 10)° = 90 degrees
10x + 10 = 90
collect the like terms
10x = 90 - 10
subtract the values
10x = 80
x = 8
Learn about Rhombus at: https://brainly.com/question/26154016
#SPJ1
triangle ABC is shown in the diagram. The links of the sides are in terms of the variable n, where n >4. complete the inquality

Answers
9514 1404 393
Answer:
m∠B < m∠A < m∠C
Step-by-step explanation:
We can work with the triangle inequality to find that the side measures form a triangle when n > 5/4. For the given value of n ≥ 4, we don't need to be concerned with whether a triangle is formed or not.
For n = 4, the side lengths are ...
a = 2(4) = 8
b = (4) +3 = 7
c = 3(4) -2 = 10
The longest side is opposite the largest angle, so the ordering of angles is ...
m∠B < m∠A < m∠C
_____
The triangle inequality requires all of these inequalities be true:
a+b > c ⇒ 3n+3 > 3n-2 . . . always trueb+c > a ⇒ 4n+1 > 2n ⇒ n > -1/2c+a > b ⇒ 5n-2 > n+3 ⇒ n > 5/4That will be the case for n > 5/4. The attached graph shows the sides and angles keep the same order for n > 3.

Answer:
M- B M-A M-C
Step-by-step explanation:
yw
Please helpppp
side lengths, surface areas, and volumes fo...
a designer builds a model of a sports car. the finished model is exactly the same shape as the original, but smaller. the scale factor is 3:11
(a) find the ratio of the surface area of the model to the surface area of the original.
(b) find the ratio of the volume of the model to the volume of the original.
(c) find the ratio of the width of the model to the width of the original.
nrite these ratios in the format m:n.
surface area:
volume:
width:
Answers
The ratios are: surface area 9:121, volume 27:1331, width 3:11.
(a) The ratio of the surface area of the model to the surface area of the original can be found by using the scale factor to find the ratio of the corresponding side lengths. Since surface area is proportional to the square of the side length, we can use this ratio squared to find the ratio of the surface areas.
The ratio of the corresponding side lengths is 3:11, so the ratio of the surface areas is (3/11)^2, which simplifies to 9/121.
Therefore, the ratio of the surface area of the model to the surface area of the original is 9:121.
(b) The ratio of the volume of the model to the volume of the original can be found using the same method as above, but with volume instead of surface area. Since volume is proportional to the cube of the side length, we can use this ratio cubed to find the ratio of the volumes.
The ratio of the corresponding side lengths is 3:11, so the ratio of the volumes is (3/11)^3, which simplifies to 27/1331.
Therefore, the ratio of the volume of the model to the volume of the original is 27:1331.
(c) The ratio of the width of the model to the width of the original can be found directly from the scale factor, since width is one of the corresponding side lengths.
The ratio of the corresponding side lengths is 3:11, so the ratio of the widths is 3:11.
Therefore, the ratio of the width of the model to the width of the original is 3:11.
Overall, the ratios are: surface area 9:121, volume 27:1331, width 3:11.
Learn more about surface area here, https://brainly.com/question/76387
#SPJ11
3. Chante claims that two circles given by (x+2)^2+(y−4)2=49 and x^2+y^2−6x+16y+37=0 are externally tangent. She is right. Show that she is
Answers
Since the distance between the centers is 10 and the radius of both circles is 7, the two circles are externally tangent.Therefore, Chante is right.
To prove that two circles are externally tangent, we need to show that their radii are equal and the distance between their centers is equal to the sum of their radii.
We can find the equation of the first circle to be (x+2)^2+(y−4)^2=49, which has a radius of 7.
For the second circle, we can rewrite the equation as x^2+y^2−6x+16y−37=0, which has a radius of sqrt(37).
Since the radius of both circles is 7, they are equal.
To find the distance between their centers, we can use the Pythagorean theorem. The distance between the centers is the square root of (6^2 + 16^2) = sqrt(100) = 10.
Since the distance between the centers is 10 and the radius of both circles is 7, the two circles are externally tangent.
Therefore, Chante is right.
the correct question is: Chante claims that two circles given by (x+2)^2+(y−4)2=49 and x^2+y^2−6x+16y+37=0 are externally tangent. She is right. Show that she is right.
Learn more about distance here
https://brainly.com/question/28956738
#SPJ4
5. A cruise ship travels at a constant speed of 17.25 miles per hour for
hours. What distance did the cruise ship travel?
Answers
A worker is stacking boxes. One stack has boxes that are 2 inches high. The other stack has boxes that are 5 inches high. At what height will the two stacks of boxes be equal in height?
Answers
Answer:
10
Step-by-step explanation:
With this question you must find the LCM for 2 and 5.
Multiples of 2= 2,4,6,8,10
Multiples of 5= 5,10
10 is the least common multiple making it the first number that the boxes can be at the same height with.
Answer:
7
Step-by-step explanation:
Factor the expression.
5x2 + 3x - 2
Answers
Answer: (5x−2)(x+1)
If I Helped, Please Mark Me As Brainliest, Have A Great Day :D
Answer:
Factor by grouping.
( 5 x − 2 ) ( x + 1 )
Step-by-step explanation:
der the following numbers from least to gre: -(1)/(2), and -1 to help us! Let's take a look. -80%,-0.25 der the numbers from least to greatest
Answers
The given numbers -80%, -0.25 can be arranged in ascending order as follows: -80%, -0.25.
To arrange the numbers -80% and -0.25 in ascending order, we need to compare their values.
First, let's convert -80% to a decimal. To do this, we divide -80% by 100, which gives us -0.8.
Now we have -0.8 and -0.25. Since both numbers are negative, the greater magnitude indicates the smaller value. In this case, -0.25 has a smaller magnitude than -0.8, so it is the smaller number.
Therefore, the numbers can be arranged in ascending order as follows: -0.25, -0.8.
Learn more about ascending order here:
https://brainly.com/question/30227337
#SPJ11
hi who els is itilian , indian, greek ,german?
or is it just me?
Answers
Answer:
Im 25% Italian And 50% dutch
Step-by-step explanation:
Answer:
no
Step-by-step explanation:
na holmes
Still on a quest to determine a mathematical relationship between these two quantities, you collect a set of data points as follows.
points : -8, -6, -2, 8, 16
percentage points : 9, -9, -18, -63, -99
where
denotes the previous day's change in the Dow Jones, measured in points; and
denotes the net approval rating for the president of the United States, measured in percentage points.
Four of these five data points exactly fit a linear model =()
.
By computing slopes, determine which of the five points is not a perfect fit, and explain your answer.
Remove the point you found in part (a). Then, find a slope-intercept equation for the linear model =+
that passes through the remaining four data points.
In one "when-then" sentence, explain the practical meaning of the
-intercept of your linear model.
(How should we understand the meaning of that number, in terms of previous day's change in the Dow Jones and/or net approval rating for the president of the United States? Include units in your explanation as appropriate.)
In one sentence, explain the practical meaning of the slope of your linear model.
(How should we understand the meaning of that number, in terms of previous day's change in the Dow Jones and/or net approval rating for the president of the United States? Include units in your explanation as appropriate.)
Answers
The point (16, -99) is not a perfect fit in the linear model, and the slope-intercept equation for the remaining four data points (-8, 9), (-6, -9), (-2, -18), and (8, -63) is y = (-15/2)x + 3; the y-intercept (3) represents the net approval rating for the president when there is no change in the Dow Jones, and the slope (-15/2) indicates that for every 1-point increase in the Dow Jones, the net approval rating is expected to decrease by 7.5 percentage points.
To determine which point is not a perfect fit in the linear model, we need to compute the slopes for each pair of consecutive data points.
The slope of a linear model represents the rate of change between the two variables.
Using the given data points:
Points: -8, -6, -2, 8, 16
Percentage Points: 9, -9, -18, -63, -99
Let's compute the slopes:
Slope between (-8, 9) and (-6, -9):
slope = (change in percentage points) / (change in points)
slope = (-9 - 9) / (-6 - (-8))
slope = -18 / 2
slope = -9
Slope between (-6, -9) and (-2, -18):
slope = (-18 - (-9)) / (-2 - (-6))
slope = -9 / 4.0
slope = -2.25
Slope between (-2, -18) and (8, -63):
slope = (-63 - (-18)) / (8 - (-2))
slope = -45 / 10
slope = -4.5
Slope between (8, -63) and (16, -99):
slope = (-99 - (-63)) / (16 - 8)
slope = -36 / 8
slope = -4.5
The slopes for the first three pairs of points (-9, -2.25, -4.5) match, indicating a consistent linear relationship.
However, the slope between the last two points is -4.5, not -4.25 like the others.
Therefore, the point (16, -99) is not a perfect fit.
Removing the point (16, -99), we have four remaining data points:
(-8, 9), (-6, -9), (-2, -18), and (8, -63).
To find the slope-intercept equation for the linear model that passes through these four points, we can use the formula:
y = mx + b
Using the slope formula with two of the remaining points:
-9 = m(-6) + b
-18 = m(-2) + b
Solving these two equations simultaneously, we find:
m = -9/4
b = 9/2
So the slope-intercept equation for the linear model is:
y = (-9/4)x + 9/2
The practical meaning of the y-intercept (9/2) is that when the previous day's change in the Dow Jones is 0 points, the net approval rating for the president of the United States is expected to be 9/2 percentage points, or 4.5 percentage points.
The practical meaning of the slope (-9/4) is that for every 1-point increase in the previous day's change in the Dow Jones, the net approval rating for the president of the United States is expected to decrease by 9/4 percentage points, or 2.25 percentage points.
For similar question on linear model.
https://brainly.com/question/31265606
#SPJ11
what is a type ii error? rejecting a false null hypothesis accepting a false alternate hypothesis rejecting a false alternate hypothesis failing to reject a false null hypothesis
Answers
A type II error is a statistical term used to describe the failure to reject a false null hypothesis. It occurs when the null hypothesis is actually false but is not rejected because the statistical test failed to find significant evidence against it.
In other words, it happens when an alternative hypothesis is true, but we fail to reject the null hypothesis.
Types of errors in hypothesis testing
There are two types of errors in hypothesis testing:
Type I error: Rejecting a true null hypothesis
Type II error: Failing to reject a false null hypothesis.Type I error occurs when a true null hypothesis is rejected while Type II error occurs when a false null hypothesis is not rejected. These types of errors are inversely related, meaning that a decrease in one type of error causes an increase in the other.
You can learn more about type II errors at: brainly.com/question/30403884
#SPJ11
HEY CAN ANYONE ANSWER DIS PLS!!

Answers
X= -2
If you can get the answer from that, great. If not then oof
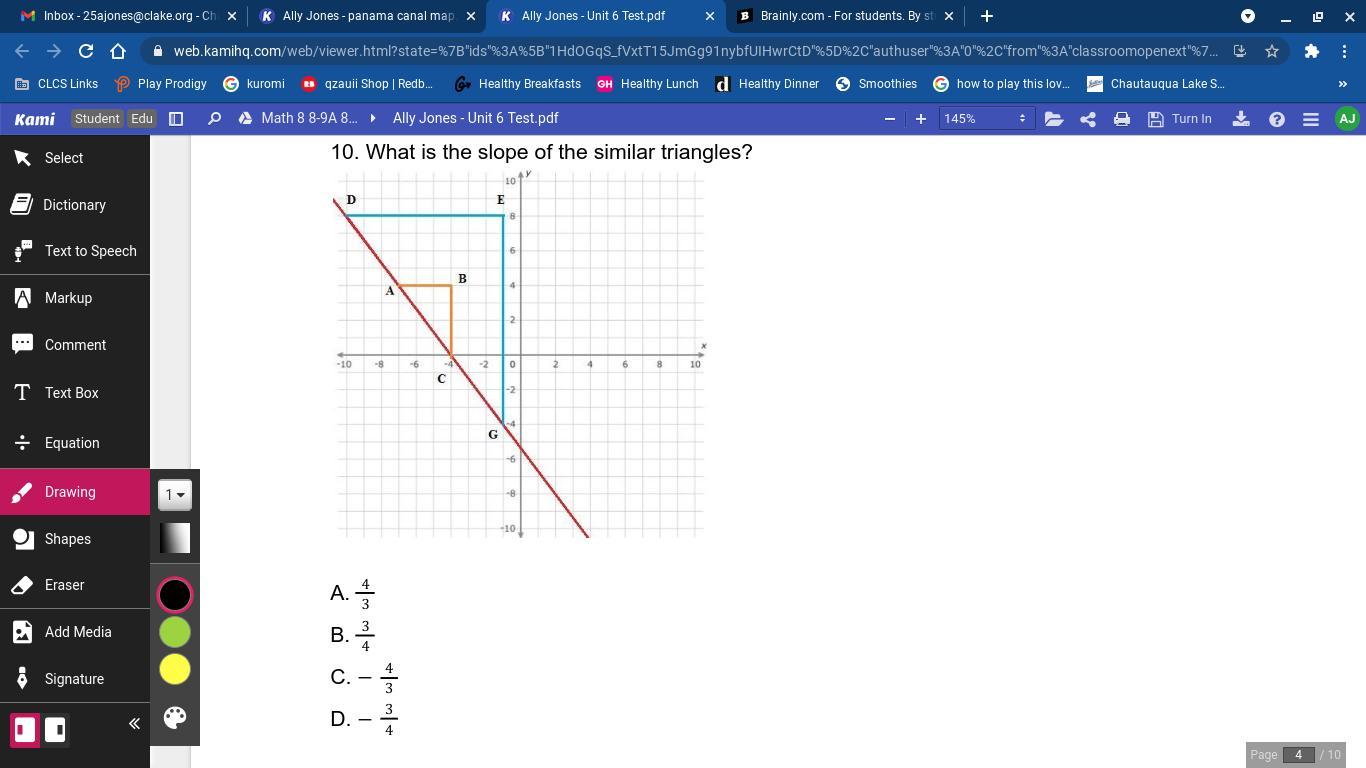
What is the slope of the similar triangles?
Answers
5-6 practice the remainder and factor theorems 5) If f(x) = 3x2 -9x -20, find the value of f(5) using synthetic substitution.
a. 0
b. 10
c. 15
d. -7
6) if f(x) = x3+8x+24, then find f(-2) using synthetic substitution.
a. 12
b. 8
c. 0
d. -6
Answers
the value of f(5) is 10, which is option (b) , the value of f(-2) is -12, which is option (d). To find the value of f(5) using synthetic substitution, we first set up the synthetic division table as follows:
5 | 3 -9 -20
|||___
| | |
We write the coefficients of the polynomial in the top row of the table and the root (in this case, 5) outside the division symbol. We then bring down the first coefficient (3) and multiply it by the root to get 15, which we write below the second coefficient (-9). We add 15 and -9 to get 6, which we then multiply by the root to get 30, which we write below the third coefficient (-20). We add 30 and -20 to get 10, which is the remainder. Therefore, the value of f(5) is 10, which is option (b).
6) To find f(-2) using synthetic substitution, we set up the synthetic division table as follows:
-2 | 1 0 8 24
|_|||
| | | |
We write the coefficients of the polynomial in the top row of the table and the root (in this case, -2) outside the division symbol. We then bring down the first coefficient (1) and multiply it by the root to get -2, which we write below the second coefficient (0). We add -2 and 0 to get -2, which we then multiply by the root to get 4, which we write below the third coefficient (8). We add 4 and 8 to get 12, which we then multiply by the root to get -24, which we write below the fourth coefficient (24). We add 12 and -24 to get -12, which is the remainder. Therefore, the value of f(-2) is -12, which is option (d).
To know more about synthetic substitution, click here:
brainly.com/question/29253953
#SPJ4