Marc has 80 blue marbles , and he wants to give away 15% of them to his friends . How many blue marbles will he give away? Proportions Marc will give away blue marbles.
Answers
Answer:
12 marbles
Step-by-step explanation:
0.15 times 80= 12
so
15% of 80 is 12
Related Questions
A rotating light is located 13 feet from a wall. The light completes one rotation every 5 seconds. Find the rate at which the light projected onto the wall is moving along the wall when the light's angle is 10 degrees from perpendicular to the wall.
Answers
Answer:
42.115 ft/s
Step-by-step explanation:
The distance from the point closest to the light is given by
d = (13 ft)tan(α)
where,
α=angle from perpendicular.
Since the light travels through an angle of 2π radians in 5 seconds, the angle can be represented by
α = πt . . . . radians
and the rate of change of α is dα/dt = π (radians/second)
The rate of change of distance is:
dd/dt = (13 ft)sec(α)²(dα/dt) = (13π)(sec(10°)²) ft/s ≈ 42.115 ft/s
Molly's scout troop sold 148 boxes of cookies last month and 165 boxes this month. Find the percent of increase, rounded to the nearest tenth of a percent.
Answers
The percent of the increase, rounded to the nearest tenth of a percent, concerning the sales of boxes of cookies that Molly sold last month and this month, is 11.5%.
How is the percentage increase determined?The percentage increase can be determined by finding the difference or the amount of increase in sales.
This difference is divided by the previous month's sales and multiplied by 100.
The total number of boxes of cookies Molly's Scout Troop sold last month = 148
The total number sold this month = 165
The increase = 17 (165 - 148)
Percentage increase = 11.5% (17 ÷ 148 x 100)
Learn more about percentage increases at https://brainly.com/question/28398580.
#SPJ1
The graph below shows a line of best fit for data collected on the distance drivers traveled as a function of time. Which of the following is the equation of the line of best fit? A. B. C. D.
Answers
The equation for the line of best fit is given as follows:
y = 50x/3.
How to define a linear function?The slope-intercept equation for a linear function is presented as follows:
y = mx + b.
The parameters of the definition of the linear function are given as follows:
m represents the slope of the function, which is by how much the dependent variable y increases(positive) or decreases(negative) when the independent variable x is added by one.b represents the y-intercept of the function, representing the numeric value of the function when the input variable x has a value of 0. On the case of the graph, the intercept is given by the value of y at which the graph crosses or touches the y-axis.From the graph, when x = 0, y = 0, hence the intercept b is given as follows:
b = 0.
Hence:
y = mx.
When x = 3, y = 50, hence the slope m is given as follows:
3m = 50
m = 50/3.
Hence the equation is:
y = 50x/3.
More can be learned about linear functions at https://brainly.com/question/15602982
#SPJ1

Help, I need to know this extension.

Answers
Answer:
10
Step-by-step explanation:
We know that area is 50km^2 and to find area we know the formula it is Area = base * height, 50 = b*5, so b must be 10
HELPPP MEEE PLEASEE WITH THIS QUESTION

Answers
The values of x and y are given as follows:
x = 18.\(y = 6\sqrt{10}\)What is the geometric mean theorem?The geometric mean theorem states that the length of the altitude drawn from the right angle of a triangle to its hypotenuse is equal to the geometric mean of the lengths of the segments formed on the hypotenuse.
The bases for this problem are given as follows:
2 and x.
The altitude is given as follows:
6.
Hence the length x is given as follows:
2x = 6²
2x = 36
x = 18.
Applying the Pythagorean Theorem, the length y is given as follows:
y² = 18² + 6²
y² = 360
\(y = \sqrt{36 \times 10}\)
\(y = 6\sqrt{10}\)
More can be learned about the geometric mean theorem at brainly.com/question/10216660
#SPJ1
A biologist takes a sample of 100 grass plants to measure stem length. The following data were obtained: Length (cm) Frequency 226 927 1028 1229 2030 1931 1332 15Calculate the mean length per stem.

Answers
Solution
To get FX
Length Times Frequency
Let's sum all the FX together
\(\begin{gathered} \Sigma fx=2923 \\ \\ \end{gathered}\)Average, also called the arithmetic mean, is the sum of all the values divided by the number of values. Whereas, mean is the average in the given data. In statistics, the mean is equal to the total number of observations divided by the number of observations (total frequency).
\(\text{Mean = }\frac{2923}{100}=29.23\)
-3/7 × - 1 2/3
what is the answer
Answers
Answer:
\(\boxed{\frac{5}{7} }\)
Step-by-step explanation:
\(-\frac{3}{7} \times (- 1 \frac{2}{3} )\)
\(= -\frac{3}{7} \times (- \frac{5}{3} )\)
\(= \frac{5}{7}\)
Answer:
5/7
Step-by-step explanation:
do you get the answer?
2
1
-1
-2
Determine the period.
2 4
6 8 10 12 14
Acellus

Answers
According to the information we can infer that the period of the graph is 8.
How to determine the period of the graph?To determine the period of the graph we have to consider that the period of a grah is the distance between rigdes. So, in this case we have to count what is the difference between each rigde.
In this case, the distance between rigdes is 8 units because the first is located in the line 1 an the second is located in the line 9. So we can conclude that the period of the graph is 8.
Learn more about period in: https://brainly.com/question/23532583
#SPJ1
HELP ME WITH A MATH PROBKEM Type a number that has a value less than 4.7|
Answers
Answer:
i think
all the numbers between
0 to 4.6
The volumes of two similar figures are given. The surface area of the larger figure is given. Find the surface area of the smaller figure.
V= 160 meters cubed
V= 2500 meters cubed
S.A. = 1400 meters squared
Answers
Answer:
Since the figures are similar, their corresponding side lengths are proportional.
Let x be the scale factor between the larger and smaller figures. Then, the volume of the larger figure is x^3 times the volume of the smaller figure.
We can set up an equation to solve for x:
2500 = x^3 * 160
Divide both sides by 160:
x^3 = 2500/160
x^3 = 15.625
Take the cube root of both sides:
x = 2.5
So, the scale factor between the larger and smaller figures is 2.5.
Since surface area is proportional to the square of the scale factor, we can set up another equation to solve for the surface area of the smaller figure:
S.A. of smaller figure / S.A. of larger figure = (scale factor of smaller figure)^2 / (scale factor of larger figure)^2
Solving for the surface area of the smaller figure:
S.A. of smaller figure / 1400 = 2.5^2 / 1^2
S.A. of smaller figure / 1400 = 6.25
S.A. of smaller figure = 6.25 * 1400
S.A. of smaller figure = 8750
Therefore, the surface area of the smaller figure is 8750 meters squared.
Step-by-step explanation:
Find the value of EC.
13
12
E
B
EC = [?]
![Find the value of EC.1312EBEC = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/8Ol9jYaoZfJnYH3cmEhQvJeLQL1cbPeJ.png)
Answers
Answer:
8Step-by-step explanation:
NOT 5.
_____________________
Firstly note that the radius of the circle is 13 ( centre to D )
Thus the distance from B to the centre is 13
Thus B → E → centre is a right triangle and distance from centre to E (x) can be calculated using Pythagoras' identity, that is
x² + 12² = 13²
x² + 144 = 169 ( subtract 144 from both sides )
x² = 25 ( take the square root of both sides )
x = = 5
The distance from the centre to C ( the radius ) is 13, thus
x + EC = 13, that is
5 + EC = 13 ( subtract 5 from both sides )
EC = 8
Answer:
The answer is 8
Step-by-step explanation:
Will mark brainliest.

Answers
The solution is, the value of the variables are x = 40 and, y = 160.
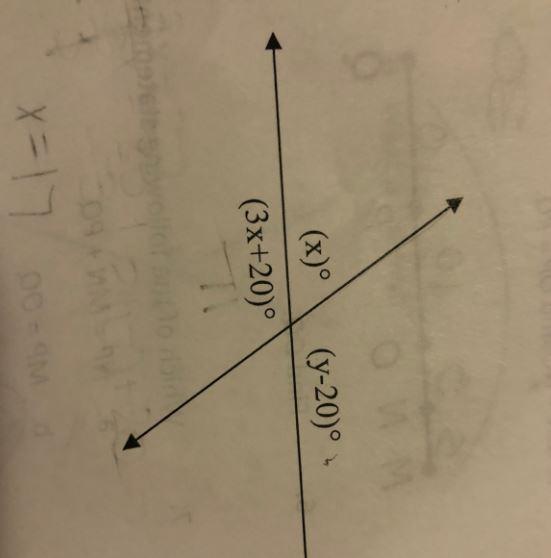
Notice that "x" and "3x+20" are supplementary angles so their sum is 180°
(x) + (3x + 20) = 180
4x + 20 = 180
4x = 160
x = 40
To solve for "y", you have 2 options: either notice that "x" and "y-20" are supplementary angles so their sum is 180° or notice that "3x + 20" and "y - 20" are vertical angles so are equal to each other. I am going to solve using the first option because it is less work.
(x) + (y - 20) = 180°
40 + y - 20 = 180
y + 20 = 180
y = 160
Answer: x=40, y=160
The solution is, the value of the variables are x = 40 and, y = 160.
To learn more on angle click:
brainly.com/question/28451077
#SPJ1
complete question:
Find the value of each variable
Rachel is making nachos for a party the recipe calls for 2/3 cup of cheese for each plate of nachos how many full plate of nachos can Rachel make with 5 cups of cheese how many more cups of cheese would Rachel need to make 9 plates of nachos
Answers
Answer:
7 plates1 cupStep-by-step explanation:
If we let c and p represent the cups of cheese and plates of nachos, we have ...
c = 2/3p . . . . . each plate of nachos requires 2/3 cups of cheese
Solving for p, we find ...
(3/2)c = p . . . . . multiply by 3/2
Then for 5 cups of cheese, we have ...
(3/2)(5) = p = 15/2 = 7 1/2 . . . . plates of nachos
5 cups of cheese will make 7 full plates of nachos.
__
For 9 plates of nachos, we need ...
c = 2/3(9) = 6 . . . . . . cups of cheese
Since we have 5 cups of cheese, we need 1 more cup of cheese to make 9 plates of nachos.
awnser the qusetion 9iu523hb5hn33

Answers
The order of the matrices of each product is given as follows:
AB is nonexistent, BA is nonexistent.
How to apply multiplication of matrices?Multiplication of matrices is applied multiplying the rows of the first matrix by the columns of the second matrix, and hence the number of columns of the first matrix must be equal to the number of rows of the second matrix.
For the product AB, we have that:
A has four columns.B has two rows.Hence the product is nonexistent.
For the product BA, we have that:
B has four columns.A has two rows.Hence the product is nonexistent.
More can be learned about multiplication of matrices at https://brainly.com/question/24274686
#SPJ1
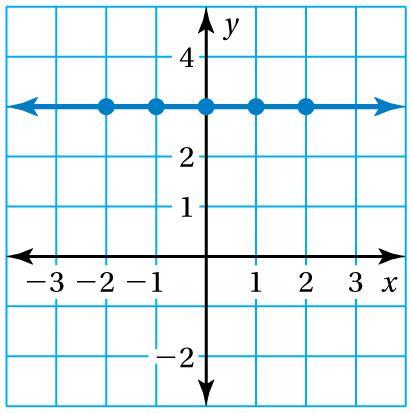
Use the graph to write a linear function that relates y to x
y=
Answers
HELP DUE SUPER SOON!!
A university has 32,040 students. In a random sample of 270 students, 18 speak three or more languages
Predict the number of students at the university who speak three or more languages.
The expected number of students at the university who speak three or more languages is

Answers
Answer:
2022 students
Step-by-step explanation:
Since 18 out of 270 students speak three or more languages, a prediction would be 30,330 x 18/270 = 2,022 students
6. Solve for y. 12y - 10 = 14y
02
0 5
O-5
O-2
Answers
Answer:
can you pls clear your questions?
5 ( 6.2 + z); z = 3.8
Answers
Answer:
50
Step-by-step explanation:
Answer:
50
Step-by-step explanation:
substitue z, then multiply by 5
Khadija went to the store to buy some apples. The price per pound of the apples is $7.50 per pound and she has a coupon for $1.75 off the final amount. With the coupon, how much would Khadija have to pay to buy 4 pounds of apples? Also, write an expression for the cost to buy

Answers
The final cost of 4 pounds is $28.25 and the final cost of p pounds is $4.
Expression for the cost to buy is, Cost(x) = $7.50x - $1.75
What is the cost price?The cost price is the price from which the seller buys the product. An expression simply consists of one or more numbers that are along the operation that is given.
In this case, the price per pound of the apples is $7.50 per pound and he has a coupon for $1.75 off the final amount.
The amount to amount that Khajida has to pay to buy 4 pounds of apples will be:
7.50p - 1.75 =
where P = number of pounds
p = 4
This will be:
5.50p - 2.5
7.5(4) - 1.75
27.5 - 1.75
28.25
The amount paid is $28.25.
Therefore, the final cost of 4 pounds: $28.25.
The final cost of p pounds: 4 dollars
To write an expression for the cost to buy x pounds of apples with the coupon, we can use the formula:
Cost = price per pound * number of pounds - coupon amount
Using this formula, we can write:
Cost(x) = $7.50x - $1.75
Where x represents the number of pounds of apples Khadija wants to buy.
Learn more about cost price, here:
https://brainly.com/question/29237727
#SPJ1
Solve this equation using number sense 10k + 5 = 65
Answers
Answer
k = 6
Explanation
We are aksed to ssolve the given equation
10k + 5 = 65
Subtract 5 from both sides
10k + 5 - 5 = 65 - 5
10k = 60
Divide both sides by 10
(10k/10) = (60/10)
k = 6
To check, this is when number sense comes into play.
With k = 6,
10k + 5 = 65
10(6) + 5 = 65
60 + 5 = 65
65 = 65
Meaning the solution iss correct.
Hope this Helps!!!
Solve y = ax² + c for x.
O x
x= ± √ay-c
O
O
x = ±₁
X=
X=
у-с
a
y
y + c
a

Answers
In the quadratic equation y = a\(x^{2}\) + c ,the value of x = ± \(\sqrt \frac{y-c}{a}\)
A quadratic equation is any equation containing one term wherein the unknown is squared and no term wherein it's far raised to a higher power.
A quadratic equation is an algebraic equation of the second degree in x. The quadratic equation in its standard form is ax2 + bx + c = 0, in which a and b are the coefficients, x is the variable, and c is the constant term.
To find the value of x
Assuming \(a\neq o\)
First, subtract c from both the sides to get:
\(y-c=ax^{2}\)
then, divide both sides by \(a\) and transpose to get:
\(x^{2} =\frac{y-c}{a}\)
So, \(x\) must be a square root of \(\frac{y-c}{a}\) and we can deduce:
\(x=\) ± \(\sqrt \frac{y-c}{a}\)
Learn more about quadratic equations here brainly.com/question/1214333
#SPJ9
Find the area of the shaded regions. Give your answers as a completely simplified exact value in terms of pi (no approximations)

Answers
Go in go knbjjjjb bxh b
GRAPHS AND FUNCTIONS
Graphing a piecewise-defined function:
Suppose that the function f is defined, for all real numbers, as follows.
Look at photo for problem! Thank you! Please tell me if it’s a hollow dot or a solid dot for the points!

Answers
A graph of the piecewise function is shown on the coordinate plane in the image attached below.
What is a piecewise-defined function?In Mathematics and Geometry, a piecewise-defined function is a type of function that is defined by two (2) or more mathematical expressions over a specific domain.
Generally speaking, the domain of any piecewise-defined function simply refers to the union of all of its sub-domains. By critically observing the graph of this piecewise-defined function, we can reasonably infer and logically deduce the following inequality rules for its domain;
x < 1 represents a hollow dot.
x = 1 represents a solid dot.
x > 1 represents a hollow dot.
Read more on piecewise function here: brainly.com/question/18670055
#SPJ1

Shannon is on a long road trip. So far, she has driven 210 miles in 180 minutes. If she has 280 miles left on her trip, how many minutes does she have left to drive, if she continues at the same rate?
Answers
Answer:
467.6 miles
Step-by-step explanation:
Unit rate x 280 = 467.6
HOPE THIS HELPS
First figure out the speed.
Speed = Distance (miles) /Time (mph)
Our units are per hour for this formula, so change it from minutes to hours.
180 minutes = 3 Hours
Speed = 210/3 = 70mph
Now we have to figure out how many minutes she has left to drive (time).
Time = Distance / Speed
280 Miles / 180mph = 1.555556 hours.
Now convert this back to minutes by multiplying by 60.
1.555556 x 60 = 93.3 minutes (93minutes)
The answer is 93 minutes
Madelyne made 2 liters of fruit punch for her party. Her brother
drinks 500 milliliters before the party. How many milliliters of punch
does she have left?
A. 1.5 liters
B. 15 milliliters
10. Cassandra needs 2 meters of string
C. 150 milliliters
D. 1,500 mililiters
centimeters of string do
Answers
Answer: D 1,500
Step-by-step explanation:
Because there is 2,000 milliliters in 2 liters, so if we do 2,000 - 500 we get 1,500 left
Answer:
Both A and D
Step-by-step explanation:
Because 500 milliters is half of one liter which makes the total 1.5 liters or 1500 mililliters
The options are: 3/10, 65%, 3/7, 70%

Answers
Answer:
70%
Step-by-step explanation:
there are 20 total marbles and only 14 are not blue so 14/20 = 7/10 = 70%
In a recent survey of 36 people, 18 said that their favorite color of car was blue.
What percent of the people surveyed liked blue cars? Explain your answer with every step you took to get to it.
Answers
Answer: The percentage of people surveyed who liked blue cars is 50%.
Step-by-step explanation:
Total number of people partaking in survey= 36
number of people who like blue cars= 18
therefore, fraction of people who liked blue cars= \(\frac{18}{36}\)
hence, percentage of people who liked blue cars= (18/36)*100 %
= 50%
To learn more about percentages visit the link below:
https://brainly.com/question/30399396
Answer:
Percentage of people who like blue-coloured cars is 50%
Number of people who were surveyed=36
Number of people who like blue-colored cars=18
Therefore, Percentage of people who like blue cars= (Number of people who like blue cars/ Number of people who were surveyed)*100
=(18/36)*100
=50%
Read more about percentage
https://brainly.in/question/21062337#:~:text=Answer%3A,has%20no%20unit%20of%20measurement.
4. Triangle Relationships- Interior and Exterior Angles
Find the measure of angle 1 and angle 2. Be sure to show all work related to each answer.
S
a. m21
42°
1/2
30°
M
b. M22
A

Answers
Answer:
Value of ∠1 = 102°
Value of ∠1 = 72°
Step-by-step explanation:
Given:
∠ S = 42°
∠ A = 30°
Find:
Value of ∠1
Value of ∠2
Computation:
Using angle sum property;
Sum of all interior angle of a triangle = 180°
∠ S + ∠ A + ∠ 1 = 180
42 + 30 + ∠ 1 = 180
72 + ∠ 1 = 180
∠ 1 = 180 - 72
∠ 1 = 102
Value of ∠1 = 102°
∠ 1 and ∠ 2 makes a straight line
So,
∠ 1 + ∠ 2 = 180
102 + ∠ 2 = 180
∠ 2 = 180 - 102
∠ 2 = 72
Value of ∠1 = 72°
Find the difference between the actual quotient and the estimated quotient of 54,114÷29 . (Dividend is rounded off to nearest thousand and divisor to nearest ten)
Answers
The difference between the actual quotient and the estimated quotient of 54,114 ÷ 29 is approximately 66.3448275862068965517241379.
To find the difference between the actual quotient and the estimated quotient of 54,114 ÷ 29, we need to first calculate the actual quotient and then the estimated quotient.
Actual quotient:
Dividing 54,114 by 29, we get:
54,114 ÷ 29 = 1,866.3448275862068965517241379 (approximated to 28 decimal places)
Estimated quotient:
Rounding the dividend, 54,114, to the nearest thousand gives us 54,000. Rounding the divisor, 29, to the nearest ten gives us 30. Now, we can perform the division with the rounded values:
54,000 ÷ 30 = 1,800
Difference between actual and estimated quotient:
Actual quotient - Estimated quotient = 1,866.3448275862068965517241379 - 1,800 = 66.3448275862068965517241379
For mor such questions on quotient visit:
https://brainly.com/question/11418015
#SPJ8
a rectangle with a width of 30 centimeters has a perimiter of 100 centimeters to 160 centimeters graph a compound inequality
Answers
Answer:
5 ≤ L ≤ 35
Step-by-step explanation:
Let w represent the width of the rectangle.
The perimeter (P) of the rectangle is given by:
P = 2w + 2L
Where L is the length of the rectangle.
We know that w = 30 cm and that the perimeter is between 100 and 160 cm. We can now set up our compound inequality:
100 ≤ 2(30) + 2L ≤ 160
100 ≤ 90 + 2L ≤ 160
10 ≤ 2L ≤ 70
We can now divide both sides by 2 to solve for L:
5 ≤ L ≤ 35
Therefore, the compound inequality that represents the graph of a rectangle with a width of 30 centimeters and a perimeter of 100 centimeters to 160 centimeters is: 5 ≤ L ≤ 35