Make a box-and-whisker plot of the data. 60,63,53,66,65,58,51,55,58,51,58,62,53,66,61,51,65,52,54,50
Answers
Minimum value is 50, maximum value is 66, median is 59, Q1 is 53.5 and Q3 is 65. Box-and-whisker plot:
Define whisker plot?A box plot, often referred to as a whisker plot, shows the distribution of a continuous variable along with details like the median, quartiles, and outliers. A set of data's variety is shown graphically in this way. The plot, often known as a five-number summary, presents five bits of information. The fundamental benefit of box whisker plots is that the overlap between the distributions of various qualities may be calculated by comparing them side by side.
You must determine the minimum value, maximum value, median, and quartiles in order to create a box-and-whisker plot of the provided data.
The base number is fifty.
The highest number is 66.
You must sort the data from smallest to largest in order to determine the median. The listed data are:
50, 51, 51, 52, 53, 53, 54, 55, 58, 58, 58, 60, 61, 62, 63, 65, 65, 66, 66
The middle value of the ordered data is the median. Finding the average of the two middle values is necessary since the data set (18 values) contains an even number of values:
(58 + 60) ÷ 2 = 59
Divide the ordered data into four equal sections before calculating the quartiles. The median of the lower half of the data set is the first quartile (Q1). The median of the data set's upper half represents the third quartile (Q3).
The data set's lower half consists of:
50, 51, 51, 52, 53, 53, 54, 55
The data set's upper half is as follows:
58, 58, 58, **60**, **61**, **62**, **63**, **65**, **65**, **66**, **66**
First quartile (Q1):
(53 + 54) ÷ 2 = **53.5**
Third quartile (Q3) comprises:
(65 + 65) ÷ 2 = **65**
With all of this knowledge at hand, you can now develop a box-and-whisker plan.
Given below:
To know more about whisker plot visit:
brainly.com/question/2742784
#SPJ1

Related Questions
write the equation of the line that passes through the point (-5,5) and is parallel to the line y=-3x+3
Answers
I purchased 3.4 pounds of apples for $7.29. What is the cost per pound? I need the answer fast.
Answers
Answer:
The answer is $2.14 per pound of apples.
Step-by-step explanation:
7.29/3.4= roughly 2.14.
Answer:
is 24.786
Step-by-step explanation:
multiply the numbers and that's how you get your answer and I use my calculator so I know the answer is 24.786
i need help with math two
Answers
In this case we want to show that the following quadrilaterals are equal:
because in this way we will prove that opposite angles are equal.
We first want to exchange A ⇄ C, which is a reflection across x-axis
Then, we exchange B ⇄ D, which is a reflection across y-axis.
Answer: C


Exercise 10
You randomly choose one of the tiles. Without replacing the first tile, you choose a second tile. What is the probability of the compound event? Write your answer as a fraction or percent rounded to the nearest tenth.

Answers
The probability of choosing a 5 and then a 6 is 1/49
Finding the probability of the compound eventFrom the question, we have the following parameters that can be used in our computation:
The tiles
Where we have
Total = 7
The probability of choosing a 5 and then a 6 is
P = P(5) * P(6)
So, we have
P = 1/7 * 1/7
Evaluate
P = 1/49
Hence, the probability of choosing a 5 and then a 6 is 1/49
Read more about probability at
https://brainly.com/question/31649379
#SPJ1
Question
You randomly choose one of the tiles. Without replacing the first tile, you choose a second tile. Find the probability of the compound event. Write your answer as a fraction or percent rounded to the nearest tenth. The probability of choosing a 5 and then a 6
200 sheets of paper from a printing press were inspected for smeared ink. Of the 200 sheets of paper, 17 sheets contained smeared ink. Assuming a 99% two-sided confidence interval, what is the confidence interval of the proportion smeared
Answers
Thus, with 99% confidence, we can say that the proportion of smeared ink in the 200 sheets of paper inspected falls between 1.3% and 15.7%.
To calculate the confidence interval of the proportion smeared in 200 sheets of paper inspected for smeared ink, we can use the formula:
Confidence Interval = sample proportion ± (critical value) x (standard error)
The sample proportion is the number of sheets containing smeared ink divided by the total number of sheets inspected, which is 17/200 = 0.085.
The critical value for a 99% two-sided confidence interval with 200 observations can be found using a t-distribution table or calculator, and is approximately 2.576.
The standard error can be calculated as the square root of [(sample proportion) x (1 - sample proportion) / sample size], which is the square root of [(0.085) x (1 - 0.085) / 200] = 0.028.
Plugging in these values, we get:
Confidence Interval = 0.085 ± (2.576) x (0.028)
Confidence Interval = 0.085 ± 0.072
Confidence Interval = (0.013, 0.157)
Therefore, with 99% confidence, we can say that the proportion of smeared ink in the 200 sheets of paper inspected falls between 1.3% and 15.7%. This means that we are 99% confident that the true proportion of smeared ink in the population of printed sheets falls within this range.
Know more about the confidence interval
https://brainly.com/question/20309162
#SPJ11
Suppose that QRS is isosceles with base q r. Suppose also that m q equals (5x - 14(degrees and Mr equals (4x - 2)degree
PLEASE HELP ME

Answers
Answer:
<S= 88degrees
<Q = <R = 46degrees
Step-by-step explanation:
Since the base angles of the isosceles triangle are equal hence;
<Q = <R
5x - 14 = 4x -2
5x - 4x = -2 +1 4
x = -2 + 14
x = 12
Since <Q = 5x - 14
<Q = 5(12) - 14
<Q = 60 - 14
<Q = 46degrees
Also <Q = <R = 46degrees
Similarly; <S + <Q + <R =180
<S +46 + 46 = 180
<+92 = 180
<S = 180 - 92
<S= 88degrees
1. Santiago's sister weighed 7 pounds, 14 ounces when she
was born. How many ounces did she weigh?
Answer:?
2. Polly bought a watermelon that weighed 295 ounces. What
is the weight of the watermelon in pounds and ounces?
Answer:?
3. An elephant at the zoo weighs 12.000 pounds. How many
tons does the elephant weigh?
Answer:?
Answers
Answer:
1) 126 ounces
2) 18 pounds and 7 ounces
3)6 tons
Step-by-step explanation:
What is the value of the expression h - 20 when h = 60
30
40
80
120
Answers
Answer:
The value of the expression h-20 when h = 60 is 40.
Step-by-step explanation:
If we simply substitute h with 60 (h = 60) we get:
60 - 20 60 - 20 = 40Hope this helps!!
\(\huge\text{Hey there!}\)
\(\huge\boxed{\mathsf{h - 20}}\\\\\huge\boxed{\mathsf{\rightarrow 60 - 20}}\\\\\huge\text{Start from 60 \& go DOWN -20 spaces to the}\\\huge\text{left.}\\\\\huge\boxed{\mathsf{\rightarrow 40}}\\\\\huge\text{Therefore, your answer is: \boxed{\textsf{40}}}\huge\checkmark\)
\(\huge\text{Good luck on your assignment \& enjoy your day!}\)
~\(\huge\textsf{Amphitrite1040:)}\)1. (5 pts) The (per hour) production function for bottles of coca-cola is q=1000K L
, where K is the number of machines and L is the number of machine supervisors. a. (2 pts) What is the RTS of the isoquant for production level q? [Use the following convention: K is expressed as a function of L b. (1 pt) Imagine the cost of operating capital is $40 per machine per hour, and labor wages are $20/ hour. What is the ratio of labor to capital cost? c. (2 pts) How much K and L should the company use to produce q units per hour at minimal cost (i.e. what is the expansion path of the firm)? What is the corresponding total cost function?
Answers
The RTS of the isoquant is 1000K, indicating the rate at which labor can be substituted for capital while maintaining constant production. The labor to capital cost ratio is 0.5. To minimize the cost of producing q units per hour, the specific value of q is needed to find the optimal combination of K and L along the expansion path, represented by the cost function C(K, L) = 40K + 20L.
The RTS (Rate of Technical Substitution) measures the rate at which one input can be substituted for another while keeping the production level constant. To determine the RTS, we need to calculate the derivative of the production function with respect to L, holding q constant.
Given the production function q = 1000KL, we can differentiate it with respect to L:
d(q)/d(L) = 1000K
Therefore, the RTS of the isoquant for production level q is 1000K.
The ratio of labor to capital cost can be calculated by dividing the labor cost by the capital cost.
Labor cost = $20/hour
Capital cost = $40/machine/hour
Ratio of labor to capital cost = Labor cost / Capital cost
= $20/hour / $40/machine/hour
= 0.5
The ratio of labor to capital cost is 0.5.
To find the combination of K and L that minimizes the cost of producing q units per hour, we need to set up the cost function and take its derivative with respect to both K and L.
Let C(K, L) be the total cost function.
The cost of capital is $40 per machine per hour, and the cost of labor is $20 per hour. Therefore, the total cost function can be expressed as:
C(K, L) = 40K + 20L
To produce q units per hour at minimal cost, we need to find the values of K and L that minimize the total cost function while satisfying the production constraint q = 1000KL.
The expansion path of the firm represents the combinations of K and L that minimize the cost at different production levels q.
Learn more about production
brainly.com/question/31859289
#SPJ11
Please help me, It'll mean a lot. :)

Answers
Answer
The answer is B
HELP ASAP MONEY & WAGES!

Answers
Answer: $26.70 per hour
Step-by-step explanation:
Regular hours consists of 8 hrs
Overtime hours is 12 - 8 = 4 hours
Regular pay at "x" per hour = 5(8)(x) = 40x
Overtime pay at "2x" per hour = 5(4)(2x) = 40x
Total pay = 80x
Total Pay = $2136 = 80x
\(\dfrac{\$2136}{80}=x\)
$26.70 = x
Please Help!
Which inequality does this graph show?

Answers
Answer: Y= -5x+4
Step-by-step explanation:
6-5 Practice Operations with radical expressions
1. √540
2. 3√432
3. 3√128
4. - 4√405
5. 3√-5000
Answers
The Practice Operations with radical expressions is simplified using the basic of the Algebra:
Algebraic expressions incorporating radicals are known as radical expressions. The root of an algebraic expression makes up the radical expressions (number, variables, or combination of both). The root might be an nth root, a square root, or a cube root. Radical expressions can be made simpler by taking them down to their most basic form and, if feasible, getting rid of all of the radicals.
Radical expressions are simplified by taking them down to their most basic form and, if feasible, altogether deleting the radical. An algebraic expression's numerator and denominator are multiplied by the appropriate radical expression if the denominator contains a radical expression.
Practice Operations with radical expressions are:
1) \(\sqrt{540}\) = \(\sqrt{36 * 15 }\)
= 6√15
2) \(\sqrt[3]{432}\) = \(\sqrt[3]{216*2}\)
= \(6\sqrt[3]{2}\)
3) \(\sqrt[3]{128}\) = \(\sqrt[3]{64*2}\)
= \(4\sqrt[3]{2}\)
4) \(-\sqrt[4]{405}\) = \(-\sqrt[4]{81*5}\)
= \(-3\sqrt[4]{5}\)
5) \(\sqrt[3]{-5000}\) = \(-\sqrt[3]{1000*5}\)
= \(-10\sqrt[3]{5}\)
Learn more about Radical expressions:
https://brainly.com/question/26637176
#SPJ4
If 63 users share a direct sequence CDMA system and each user has a processing gain of 511, determine the average probability of error for each user. Assumptions: 1. Perfect power control, all users are of equal power. 2. All users are orthogonal, independent, and the Gaussian approximation is valid.
Answers
The average probability of error for each user in a direct sequence CDMA system with 63 users and a processing gain of 511 can be determined using the Gaussian approximation. Under the assumptions of perfect power control and orthogonal, independent users, the average probability of error can be calculated.
In a direct sequence CDMA system, the average probability of error for each user can be calculated using the formula:
Average Probability of Error = (1 / (2 * log2(1 + Signal-to-Interference Ratio)))
To calculate the Signal-to-Interference Ratio (SIR), we need to consider the number of users and the processing gain. In this case, there are 63 users and each user has a processing gain of 511.
The SIR is given by the formula:
SIR = (Number of Users * Processing Gain) / (1 + (Number of Users - 1) * Processing Gain)
Substituting the values, we get:
SIR = (63 * 511) / (1 + (63 - 1) * 511)
Calculating the SIR, we find:
SIR ≈ 511
Now, we can calculate the average probability of error using the SIR value:
Average Probability of Error = (1 / (2 * log2(1 + 511)))
Calculating the average probability of error, we find:
Average Probability of Error ≈ 0.00286
Therefore, under the given assumptions of perfect power control, orthogonal, independent users, and the Gaussian approximation being valid, each user in the system would have an average probability of error of approximately 0.00286.
Learn more about gaussian approximation here
https://brainly.com/question/32511004
#SPJ11
Find the values of x and y.

Answers
Answer:
y=60°
x=12°
Step-by-step explanation:
because the propertiy of parallelogram is the opposite side have equal measurement.
that is why y=60°
x+3=15 the paralla side are equal
x=15°-3°
x=12°
proof》》》》x+3=
12°+3°=15°
15°=15°
Please answer this question

Answers
Answer:
3/100
Step-by-step explanation:
1 m = 100 cm
Scale factor = 3/100
Hope it helps you
Answer:
the answer would be 3/100
Use the divergence theorem to find the outward flux of F across the boundary of the region D. F = (5y ? 4x)i -(4z ? 5y)j - (3y ? 2x)k D: The cube bounded by the planes x= plus or minus 1, y= plus or minus 1, and plus or minus 1 The outward flux is
Answers
The outward flux of the vector field F across the boundary of the region D, which is the cube bounded by the planes x = ±1, y = ±1, and ±1, can be found using the divergence theorem.
The outward flux is the integral of the divergence of F over the volume enclosed by the boundary surface.The first step is to calculate the divergence of F. The divergence of a vector field F = P i + Q j + R k is given by div(F) = ∂P/∂x + ∂Q/∂y + ∂R/∂z. In this case, div(F) = ∂/∂x(5y - 4x) + ∂/∂y(-4z - 5y) + ∂/∂z(-3y - 2x). Simplifying these partial derivatives, we have div(F) = -4 - 2 - 3 = -9.
Applying the divergence theorem, we can relate the flux of F across the boundary surface to the triple integral of the divergence of F over the volume enclosed by the surface. Since D is a cube with sides of length 2, the volume enclosed by the surface is 2^3 = 8.
Therefore, the outward flux of F across the boundary of D is given by ∬S F · dS = ∭V div(F) dV = -9 * 8 = -72. The negative sign indicates that the flux is inward.
In summary, the outward flux of the vector field F across the boundary of the cube D, as described by the given vector components, is -72. This means that the vector field is predominantly flowing inward through the boundary of the cube.
Learn more about integral here: https://brainly.com/question/31433890
#SPJ11
Jessica wanted to know how much farther she ran in Week 2 than in Week 1. Her work is below.
15.05 minus 11.90 = 5.95. The decimals in the equation are all aligned. The 0 in 15.05 is crossed out and a 10 is above it. The first 5 in 15.05 is crossed out and a 6 is above it.
What mistakes did Jessica make when solving the problem? Select all that apply.
She did not align the decimal points.
She did not subtract 10 and 9 correctly.
She subtracted instead of adding.
She did not rename correctly.
PLZ HELP
Answers
Answer:
She did not subtract 10 and 9 correctly. she did not rename correctly.
Step-by-step explanation:
your welcome :) hehe
Answer:
B and DStep-by-step explanation:
It's correct look at the pic

What is the slope of a line parallel to the following line: 5x + 8y = 50
Answers
Answer:
-5/8
Step-by-step explanation:
Convert standard form to slope-intercept form to find the slope.
5x + 8y = 50
8y = -5x + 50
y = -5/8x + 50/8
Slope: -5/8
Answer:
-5/8x
Step-by-step explanation:
First you need to find the slope of the given line.
Do this by converting it to slope intercept form (y=mx+b)
Divide the whole equation by 8 to isolate the y variable.
After dividing by 8 you should now have 5/8x + y = 6.25
Now you need to subtract y and 6.25 to isolate y
5/8x - 6.25 = -y
Now you have to divide the whole equation by negative 1 to make y positive. You end up with: y = -5/8 + 6.25
We know that the slopes of parallel lines are equal. Therefore the answer is -5/8x
2 The value of y is directly proportional
to the value of x.
If y = 35 when x = 140, what is the
value of y when x=70
Answers
Answer:
y = 17.5
Step-by-step explanation:
Given that y is directly proportional to x then the equation relating them is
y = kx ← k is the constant of proportion
To find k use the condition y = 35 when x = 140, then
35 = 140k ( divide both sides by 140 )
0.25 = k
y = 0.25x ← equation of proportion
When x = 70, then
y = 0.25 × 70 = 17.5
A scale drawing of a building is shown below. The scale of the drawing is 1 cm = 5 m
What is the perimeter of the actual building?
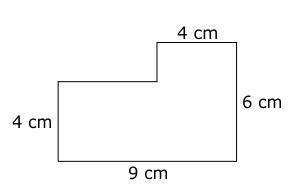
Answers
Answer:
150
Step-by-step explanation:
P = total distance
find the remaining distance which is
9- 4 = 5cm
6-4 = 2cm
P= 4+9+6+4+2+5
P= 30cm
Actual Perimeter
1cm = 5m
30 cm=?
30*5 = 150m
Answer:115
Step-by-step explanation:
Arianna deposits $500 in an account that pays 3% interest, compounded semiannually. How much is in the account at the end of 2 years.
Answers
There will be $530.68 in the account at the end of 2 years, if Arianna deposits $500 in an account that pays 3% interest, compounded semiannually.
How much is in the account at the end of 2 years?The formula accrued amount in a compounded interest is expressed as;
A = P( 1 + r/n )^( n × t )
Where A is accrued amount, P is principal, r is interest rate and t is time.
Given the data in the question;
Principal P = $500
Compounded semi annually n = 2
Time t = 2 years
Interest rate r = 3%
Accrued amount A = ?
First, convert R as a percent to r as a decimal
r = R/100
r = 3/100
r = 0.03
Plug the values into the above formula:
A = P( 1 + r/n )^( n × t )
A = $500( 1 + 0.03/2 )^( 2 × 2 )
A = $500( 1 + 0.015 )^( 4 )
A = $530.68
Therefore, the accrued amount is $530.68.
Learn more about compound interest here: brainly.com/question/27128740
#SPJ1
When parking a car in a downtown parking lot, drivers pay according to the number of hours or fraction thereof. the probability distribution of the number of hours cars are parked has been estimated as follows:
a. mean=
b. standard deviation=
the cost of parking is 5 dollars per hour. calculate the mean and standard deviation of the amount of revenue each car generates.
a. mean=
b. standard deviation
col1 x 1 2 3 4 5 6 7 8
col2 p(x) 0.229 0.113 0.114 0.076 0.052 0.027 0.031
0.358
Answers
1) a. mean = 4.164 b. standard deviation = 0.7792
2) a. mean = $20.82 b. standard deviation = $3.896
To calculate the mean of the number of hours, we multiply each possible value by its probability and then add them up,
Mean = (1)(0.229) + (2)(0.113) + (3)(0.114) + (4)(0.076) + (5)(0.052) + (6)(0.027) + (7)(0.031) + (8)(0.358) = 4.164
Therefore, the mean number of hours that cars are parked is approximately 4.164.
To calculate the standard deviation of the number of hours, we use the formula,
SD = sqrt[(1/n) * sum(p(x)*(x - mean)^2)]
where n is the sample size, p(x) is the probability of each possible value, mean is the mean of the distribution, and x is each possible value.
Plugging in the values,
SD = sqrt[(1/8) * ((1-4.164)^20.229 + (2-4.164)^20.113 + (3-4.164)^20.114 + (4-4.164)^20.076 + (5-4.164)^20.052 + (6-4.164)^20.027 + (7-4.164)^20.031 + (8-4.164)^20.358)]
SD = sqrt[(1/8) * (2.4212)]
SD = 0.7792
To calculate the mean and standard deviation of the revenue generated per car, we simply multiply the mean and standard deviation of the number of hours by the cost per hour:
Mean revenue per car = 4.164 * $5 = $20.82
Standard deviation of revenue per car = 0.7792 * $5 = $3.896
To know more about mean, here
brainly.com/question/28108712
#SPJ4
−8x−10=4x+14 what’s x
Answers
Answer:
x=-2
Step-by-step explanation:
−8x−10=4x+14
-8x-4x=14+10
-12x=24
\(\frac{-12x}{-12} = \frac{24}{-12}\)
x = -2
please help :)
Given f(x) = -x² + 9x − 17, find f(−5)
Answers
Answer: -87
Step-by-step explanation: -(−5)² + 9(−5) − 17 =
-25 - 45 - 17 = -87
Answer:
f(x)= 3
Step-by-step explanation:
If f(x) is equal to -\(x^{2}\)+9x-17 and f(-5)
You will substitute -5 where you see all the x's
-(-5)\(^{2}\)+9(-5)-17
That will equal to
-25+45-17
Combine all the like terms
This will lead you to answer 3
So, f(x) =3
Sergio poured 45/ of the soda from a 2-liter bottle for his guests. how much soda in liters is still left in the bottle?
Answers
The soda left in the bottle is 0.4 liters in a 2-liter bottle.
Let’s understand this with the concept of Ratio.
How does ratio work?
When two objects are related using numbers or amounts, the relationship is known as a ratio.
Initially, we are given that the bottle is 2 liters. From that, Sergio poured ⅘ of the soda.
So, the soda left is the initial quantity- the final quantity
= 2(initial quantity) - ⅘*2(final quantity)
=2 - 1.6= 0.4 liter
So finally, the soda left in the 2-liter bottle is 0.4 liter.
To know more about Ratios, visit: https://brainly.com/question/1706633
#SPJ4
Write the expanded form of the expression. 2(3x-5)
Answers
Answer:
6x-10
Step-by-step explanation:
2(3x-5)
6x-10
Answer:
-30
Step-by-step explanation: 2 threetimes takeawyfive
calculate the exact number of basic operation of the following examples. What is the theta and the Big O of these numbers?C(n)=∑i=0n−2(∑j=i+1n−11) C(n)=∑i=0n−1∑j=0n−1∑j=0n1
Answers
The number of basic operations and the theta and Big O of the given functions have been calculated.
The answer can be summarized as follows:
C(n) = ∑i=0 n-2(∑j=i+1n-11):
Number of basic operations = Σ(n-1-i)
\(\theta\) = Θ(n2)
Big O = O(n2)
C(n) = ∑i=0n-1∑j=0 n-1 ∑k=0 n-11:
Number of basic operations = n3
\(\theta\) = Θ(n2)
Big O = O(n2)
C(n) = ∑i=0n-2(∑j=i+1n-11) can be solved as follows:
For i = 0: i+1 = 1, i ≤ n-1
Therefore, j ranges from 1 to n-1∑j=1n-11 = n-1
For i = 1: i+1 = 2, i ≤ n-1
Therefore, j ranges from 2 to n-1∑j=2n-11 = n-2
For i = 2: i+1 = 3, i ≤ n-1
Therefore, j ranges from 3 to n-1∑j=3n-11 = n-3.......
For i = n-2: i+1 = n-1, i ≤ n-1
Therefore, j ranges from n-1 to n-1∑j=n-1n-11 = 1
Therefore, C(n) can be calculated as:
C(n) = ∑i=0n-2(n-1-i) --------------- (1)
Now, calculating the value of C(n) using the formula (1):
C(n) = (n-1) × (n-1)/2 -------------- (2)
C(n) = Θ(n2) and O(n2).
C(n) = ∑i=0n-1∑j=0n-1∑k=0
n-11 can be solved as follows: ∑k=0n-11 = n
For each value of k, there will be a different number of terms in the inner loop.
j can range from 0 to n-1.
Therefore, the inner loop will run n times for k = 0. n-1 times for k = 1 and so on.
So, the inner loop will run for a total of n times for k = 0 to n-1.
C(n) = ∑i=0n-1∑j=0n-1n = n2C(n) = Θ(n2) and O(n2).
Thus, the number of basic operations and the theta and Big O of the given functions have been calculated.
The answer can be summarized as follows:
C(n) = ∑i=0 n-2(∑j=i+1n-11):
Number of basic operations = Σ(n-1-i)
Theta = Θ(n2)
Big O = O(n2)
C(n) = ∑i=0n-1∑j=0 n-1 ∑k=0 n-11:
Number of basic operations = n3
Theta = Θ(n2)
Big O = O(n2)
To know more about loop, visit:
https://brainly.com/question/14390367
#SPJ11
3. Find \( y^{\prime} \) for the following implicit function \( y^{2}-x^{2} y=-2 \)
Answers
The derivative \(\( y' \)\) of the implicit function \(\( y^2 - xy = -2 \)\) is 0, indicating a constant slope with no change in relation to \(\( x \)\).
To find \(\( y' \)\)for the implicit function \(\( y^2 - xy = -2 \)\), we can differentiate both sides of the equation with respect to \(\( x \)\) using the chain rule. Let's go step by step:
Differentiating \(\( y^2 \)\) with respect to \(\( x \)\) using the chain rule:
\(\[\frac{d}{dx}(y^2) = 2y \cdot \frac{dy}{dx}\]\)
Differentiating \(\( xy \)\) with respect to \(\( x \)\) using the product rule:
\(\[\frac{d}{dx}(xy) = x \cdot \frac{dy}{dx} + y \cdot \frac{dx}{dx} = x \cdot \frac{dy}{dx} + y\]\)
Differentiating the constant term (-2) with respect to \(\( x \)\) gives us zero since it's a constant.
So, the differentiation of the entire equation is:
\(\[2y \cdot \frac{dy}{dx} - (x \cdot \frac{dy}{dx} + y) = 0\]\)
Now, let's rearrange the terms:
\(\[(2y - y) \cdot \frac{dy}{dx} - x \cdot \frac{dy}{dx} = 0\]\)
Simplifying further:
\(\[y \cdot \frac{dy}{dx}\) \(- x \cdot \frac{dy}{dx} = 0\]\)
Factoring out:
\(\[(\frac{dy}{dx})(y - x) = 0 \]\)
Finally, solving:
\(\[\frac{dy}{dx} = \frac{0}{y - x} = 0\]\)
Therefore, the derivative \(\( y' \)\) of the given implicit function is 0.
Learn more about derivative
brainly.com/question/29144258
#SPJ11
Which situation represents a multiplicative relationship?
There are five more trombones than trumpets.
There is a total of nine flutes and clarinets.
There are five times as many saxophones than violins.
There are 16 string instruments.
Answers
Answer:
There are five times as many saxophones than violins.
Step-by-step explanation:
times is another word indicating multiplication