LOTS OF PTS AND BRAINLIEST TO CORRECT ANSWERS!
1) Solve for x. (Attachment Below in Pic 1)
2) Find EF. (Attachment Below in Pic 2)
3) Solve for x. (Attachment Below in Pic 3)
4) Find NM. (Attachment Below in Pic 4)
TYSM TO WHOEVER HELPS!




Answers
2x+4=x+5
x=1
2x=2
Related Questions
A trader bought a computer for 43000£ and sold it at a profit of 5%.what is the selling price?
Answers
Answer:
The answer is 45150£
Step-by-step explanation:
Solution,
Given: Cost price of computer(C.P)= 43000£
Profit percent = 5%
Selling price (S.P) = ?
We know that,
Profit = Profit percent × C.P
= 5% × 43000£
= 5/100 × 430000£
= 2150£
S.P = Profit + C.P
= 2150£ + 43000£
= 45150£ Ans
The value of the selling price would be,
= £45150
What is Multiplication?To multiply means to add a number to itself a particular number of times. Multiplication can be viewed as a process of repeated addition.
Given that;
A trader bought a computer for 43000£ and sold it at a profit of 5%.
Hence, Cost price of computer(C.P)= 43000£
Profit percent = 5%
We know that,
Profit = Profit percent × C.P
= 5% × 43000£
= 5/100 × 430000£
= 2150£
Hence, S.P = Profit + C.P
= 2150£ + 43000£
= 45150£
Thus., The value of the selling price would be,
= £45150
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ2
A man received a monthly salary of $3500 together with a commission of 5% on all sales over $5000 per month. Calculate his gross salary in a month in which his sales amounted to $40,000.
Answers
Answer:
$5500
Step-by-step explanation:
3500 + 0.05 * 40,000 = 5500
His gross salary in a month in which his sales amounted to $40,000 would be; 5500 dollars.
What is the fundamental principle of multiplication?Multiplication is the mathematical operation that is used to determine the product of two or more numbers. If an event can occur in m different ways and if following it, a second event can occur in n different ways, then the two events in succession can occur in m × n different ways.
It is given that man received a monthly salary of $3500 together with a commission of 5% on all sales over $5000 per month.
Let the x represents his gross salary in a month in which his sales amounted to $40,000.
Therefore,
x = 3500 + 0.05 (40,000)
x = 3500 + 2000
x = 5500
Hence, his gross salary in a month in which his sales amounted to $40,000 would be; 5500 dollars.
Learn more about multiplications;
https://brainly.com/question/14059007
#SPJ2
9. Reason Helen is designing a corporate logo. She knows that AB congruent to CD and that angle ABF and angleCDF are right angles. Can she prove that triangleABC congruent to triangle CDA? Explain your reasoning.

Answers
For given triangles ABC and CDF, these are congruent by Angle Angle side theorem.
What is the definition of a triangle?
Triangles are polygons with three sides and three vertices in geometry. This figure is two-dimensional and has three straight sides. A triangle is a polygon with three sides. The sum of a triangle's three angles equals 180°. The triangle is contained inside a single plane. Triangles are categorised into three types based on their sides .
Based on its sides, a triangle is classified into three types:
Scalene Triangle - Each side is different in length.
Isosceles Triangle - A triangle with two sides that are equal in length and one side that is not.
Equilateral Triangle - A triangle with three equal-length sides.
Now,
As Angle-Angle-Side (AAS) Congruence Theorem: If two angles and a non-included side in one triangle are congruent to two angles and a non-included side in another triangle, the triangles are congruent.
and here AB congruent CD and angle ABF = angle CDF and
Angle AFB= Angle CFD (vertically opposite angles)
Hence,
By AAS triangle ABC is congruent to triangle CDF.
To know more about triangles visit the link
https://brainly.com/question/2773823?referrer=searchResults
#SPJ1
the slope of the tangent to the curve y^3x+y^2x^2=6 at (2 1) is
Answers
The slope of the tangent to the curve is -5/14.
Apply implicit differentiation and the product rule to the curve:
\(3y^{2} \frac{dy}{dx} x + y^{3} + 2y\frac{dy}{dx} x^{2} + y^{2}2x = 0\)
Do some rewriting
\(3xy^{2}\frac{dy}{dx} + 2x^{2}y\frac{dy}{dx} + y^{3} + 2xy^{2} = 0\)
Factor and move terms without a \(\frac{dy}{dx}\) factor to the right side
\(\frac{dy}{dx}(3xy^{2}+2x^{2}y) = -y^{3} - 2xy^{2}\)
Now divide both sides by \(3xy^{2}+2x^{2}y\) and factor where you can
\(\frac{dy}{dx} = \frac{-y^{2}(y+2x)}{yx(3y+2x)}\)
\(\frac{dy}{dx} = \frac{-y(y+2x)}{x(3y+2x)}\)
Now evaluate the given point \((2,1)\)
\(\frac{dy}{dx} = \frac{-1(1 + 2(2))}{2(3(1) + 2(2))} = \frac{-1(5)}{2(7)} = \frac{-5}{14}\)
Therefore, the slope of the tangent to the curve is -5/14.
To learn more about the slope of the tangent:
brainly.com/question/30460809
please give 100% correct
answer and Quickly ( i'll give you like )
Question An equation of the cone z = √3x2 + 3y2 in spherical coordinates is: p=3 This option This option e || O This option None of these This option
Answers
None of the options provided (e || O or None of these) accurately represent the equation of the cone z = √3\(x^{2}\) + 3\(y^{2}\) in spherical coordinates when expressed in the form p = 3.
The equation of a cone in spherical coordinates can be expressed as p = \(\sqrt{x^{2} + y^{2} + z^{2}}\), where p represents the radial distance from the origin to a point on the cone. In the given equation z = √3\(x^{2}\) + 3\(y^{2}\), we need to rewrite it in terms of p.
To convert the equation to spherical coordinates, we substitute x = p sin θ cos φ, y = p sin θ sin φ, and z = p cos θ, where θ represents the polar angle and φ represents the azimuthal angle.
Substituting these values into the equation z = √3\(x^{2}\) + 3\(y^{2}\), we get:
p cos θ = √3{(p sin θ cos φ)}^{2} + 3{(p sin θ sin φ)}^{2}
Simplifying the equation further:
p cos θ = √3\(p^2\) \(sin^2\) θ \(cos^2\)φ + 3\(p^2\)\(sin^2\) θ \(sin^2\) φ
Now, canceling out p from both sides of the equation, we have:
cos θ = √3 \(sin^{2}\) θ \(cos^{2}\) φ + 3 \(sin^2\) θ \(sin^2\) φ
Unfortunately, this equation cannot be reduced to the form p = 3. Therefore, the correct answer is "None of these" as none of the given options accurately represent the equation of the cone z = √3\(x^{2}\)+ 3\(y^{2}\) in spherical coordinates in the form p = 3.
To learn more about cone visit:
brainly.com/question/29767724
#SPJ11
pla shop mathematics

Answers
The number of trees more than 10m tall but not more than 20m tall is 18 trees.
How many of the trees are more than 10m tall but not more than 20m tall?0 < h ≤ 5 = 5
height greater than 0m less than or equal to 5m
5 < h ≤ 10 = 9
height greater than 5m less than or equal to 10m
10 < h ≤ 15 = 13
height greater than 10m less than or equal to 15m
15 < h ≤ 20 = 5
height greater than 15m less than or equal to 20m
20 < h ≤ 25 = 1
height greater than 20m less than or equal to 25m
The number of trees that are more than 10m tall but not more than 20m tall are;
10 < h ≤ 15 = 13
15 < h ≤ 20 = 5
So,
13 + 5 = 18 trees
Therefore, the total number of trees which are 10m tall but not more than 20m tall is 18 trees.
Read more on inequality:
https://brainly.com/question/25275758
#SPJ1
find dy/dx by implicit differentiation. y sin(x2) = x sin(y2)
Answers
The derivative dy/dx of the equation ysin(x^2) = xsin(y^2) is given by (sin(y^2) - ycos(x^2)2x) / (sin(x^2) - 2yxcos(y^2)).
In the given equation, y and x are both variables, and y is implicitly defined as a function of x. To find dy/dx, we differentiate each term using the chain rule and product rule as necessary.
Differentiating the left-hand side of the equation, we apply the product rule to ysin(x^2). The derivative of ysin(x^2) with respect to x is dy/dxsin(x^2) + ycos(x^2)*2x.
Differentiating the right-hand side of the equation, we apply the product rule to xsin(y^2). The derivative of xsin(y^2) with respect to x is sin(y^2) + x*cos(y^2)2ydy/dx.
Now we have two expression for the derivative of the left and right sides of the equation. To isolate dy/dx, we can rearrange the terms and solve for it.
Taking the derivative of ysin(x^2) = xsin(y^2) with respect to x using implicit differentiation yields:
dy/dxsin(x^2) + ycos(x^2)2x = sin(y^2) + xcos(y^2)2ydy/dx.
By rearranging the terms, we can solve for dy/dx:
dy/dx * (sin(x^2) - 2yxcos(y^2)) = sin(y^2) - y*cos(x^2)*2x.
Finally, we can obtain the value of dy/dx by dividing both sides by (sin(x^2) - 2yxcos(y^2)):
dy/dx = (sin(y^2) - ycos(x^2)2x) / (sin(x^2) - 2yxcos(y^2)).
Learn more about implicit differentiation here brainly.com/question/31568657
#SPJ11
WILL REWARD BRAINLIEST PLS HELP ASAP Find the total surface area.

Answers
The surface area of the rectangular prism is 88 square inches.
Given that:
Length, L = 6 inches
Width, W = 2 inches
Height, H = 4 inches
Let the prism with a length of L, a width of W, and a height of H. Then the surface area of the prism is given as
SA = 2(LW + WH + HL)
SA = 2(6 x 2 + 2 x 4 + 4 x 6)
SA = 2 (12 + 8 + 24)
SA = 2 x 44
SA = 88 square inches
More about the surface area of the rectangular prism link is given below.
https://brainly.com/question/14987814
#SPJ1
I WILL PICK BRAINLEIST!!!!!!!!! + 15 points
Rate of change tells how something....
A. constantly changes
B. can be made
C. looks and feels
Answers
Answer:
I’m going to said A
Step-by-step explanation:
If g(x) = x+8 an
and h(x) = x-2, what is the value of g(h(-8))?
Answers
\(\begin{cases} g(x) = x + 8\\\\ h(x)=x-2 \end{cases} \\\\[-0.35em] ~\dotfill\\\\ h(-8)=(-8) - 2\implies h(-8) = -10 \\\\[-0.35em] ~\dotfill\\\\ g(~~h(-8)~~)\implies g(-10)=(-10) + 8\implies g(-10)=-2\)
The area of a rectangle is 58 in². The base is 8 inches long. What is the height
Answers
Answer:
7.25 inches
Step-by-step explanation:
formula for the area of a rectangle:
base × perpendicular height
inputting what we have:
8 × height = 58
divide both sides by 8
58/8=7.25
height=7.25 inches
the matrix of a quadratic form is a symmetric matrix
Answers
The matrix of a quadratic form is always a symmetric matrix.A quadratic form is a mathematical expression that consists of variables raised to the power of two, multiplied by coefficients, and added together.
It can be represented in matrix form as Q(x) = x^T A x, where x is a vector of variables and A is the matrix of coefficients. The matrix A is known as the matrix of the quadratic form.
To show that the matrix of a quadratic form is symmetric, let's consider the expression Q(x) = x^T A x. Using the properties of matrix transpose, we can rewrite this expression as Q(x) = (x^T A^T) x. Since the transpose of a matrix A is denoted as A^T, we can see that A^T is the same as A, as A is already a matrix.
Therefore, we have Q(x) = x^T A x = x^T A^T x. This implies that the matrix of the quadratic form A is symmetric, as A^T = A. In other words, the elements of the matrix A are symmetric with respect to the main diagonal. This property holds true for any quadratic form, regardless of its coefficients or variables, making the matrix of a quadratic form symmetric.
Learn more about matrix here:
https://brainly.com/question/29000721
#SPJ11
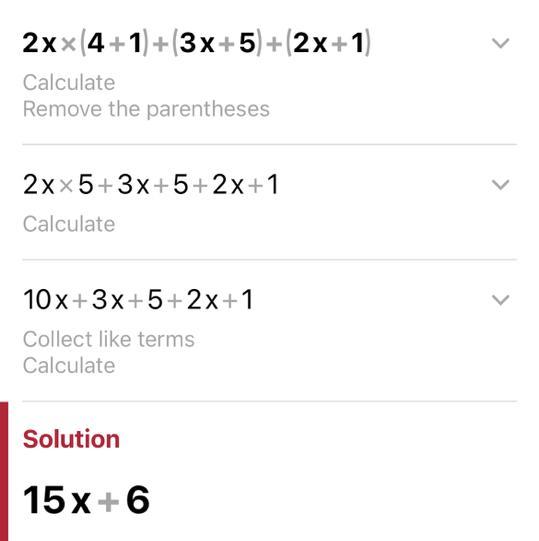
2x(4+1)+(3x+5)+(2x+1)
Answers
Isaac owns a food truck that sells tacos and burritos. He only has enough supplies to make 130 tacos or burritos. He sells each taco for $4.25 and each burrito for $8.50. Isaac must sell a minimum of $850 worth of tacos and burritos each day. If x represents the number of tacos sold and y represents the number of burritos sold, write and solve a system of inequalities graphically and determine one possible solution.
Answers
By solving linear equation, it can be calculated that x = 60 , y = 70 is one possible solution of the linear equation.
What is linear inequation?Inequation shows the comparison between two algebraic expressions by connecting the two algebraic expressions by <, >, ≤, ≥
A one degree inequation is known as linear inequation.
Let the number of tacos sold be $x and the number of burrito sold be $y
He only has enough supplies to make 130 tacos or burritos.
x + y ≤ 130 ... (1)
He sells each taco for $4.25 and each burrito for $8.50.
Isaac must sell a minimum of $850 worth of tacos and burritos each day.
4.25x + 8.5y ≥ 850
x + 2y ≥ 200 ... (2)
The inequalities has been solved graphically as;
One possible solution is x = 60, y = 70
To learn more about linear inequation visit:
brainly.com/question/24372553
#SPJ1
(11^2x × 11^1 - 6 × 121^x )÷ (5 × 121^x)
Answers
Answer:
\(\frac{1331x-6\times \:121^x}{5\times \:121^x}\)
Step-by-step explanation:
\(\frac{11^2x\times \:11^1-6\times \:121^x}{5\times \:121^x}\)
\(\mathrm{Apply\:exponent\:rule}:\quad \:a^b\times \:a^c=a^{b+c}\)
\(11^2\times \:11^1=11^{2+1}\)
\(=\frac{11^{2+1}x-6\times \:121^x}{5\times \:121^x}\)
\(\mathrm{Add\:the\:numbers:}\:2+1=3\)
\(=\frac{11^3x-6\times \:121^x}{5\times \:121^x}\)
\(11^3=1331\)
\(=\frac{1331x-6\times \:121^x}{5\times \:121^x}\)
[RevyBreeze]
Answer:
1
Step-by-step explanation:
\( \dfrac{11^{2x} \times 11^1 - 6 \times 121^x}{5 \times 121^x} = \)
\( = \dfrac{11 \times 11^{2x} - 6 \times 11^{2x}}{5 \times 11^{2x}} \)
\( = \dfrac{5 \times 11^{2x}}{5 \times 11^{2x}} \)
\( = 1 \)
Given the side lengths of 4, 5, and 6, the triangle is:
acute.
obtuse.
right.
None of these choices are correct.
Answers
Answer:
Acute
Step-by-step explanation:
It is not a right triangle. Because the biggest angle is less than , the other two angles are also, and the triangle is an (a) Acute triangle.
Explanation
Refer to the converse of the pythagorean theorem. That theorem converse has three cases.
If \(a^2+b^2 > c^2\) then the triangle is acute.If \(a^2+b^2 = c^2\) then it is a right triangle.If \(a^2+b^2 < c^2\) then the triangle is obtuse.The a,b,c refer to the side lengths. The c is the longest side.
In this case
a = 4, b = 5, c = 6
We find that \(a^2+b^2 = 4^2+5^2 = 16+25 = 41\)
And also \(c^2 = 6^2 = 36\)
Compare \(a^2+b^2 = 41\) and \(c^2 = 36\) to see that 41 is larger, so we'll go with the case \(a^2+b^2 > c^2\) to prove the triangle is acute.
You can use a tool like GeoGebra to confirm the answer is correct.
the area under the entire probability density curve is equal to___a. 0b. -1c. 1d. [infinity]
Answers
The required area under the whole probability density curve is given by option C. 1.
The area under the entire probability density curve is equal to,
As the probability density function (pdf) represents the probability of a continuous random variable.
And continuous random variable taking on a specific value within a certain range.
Since the total probability of all possible outcomes must be equal to 1.
This implies that the area under the entire probability density function (pdf) curve must also be equal to 1.
Therefore, the area under the entire probability density curve function is equal to option c. 1.
Learn more about area here
brainly.com/question/30066972
#SPJ4
(14.7+9.3) times (1/2)2
Answers
Answer:
24
Step-by-step explanation:
A rectangular restaurant kitchen has an area of 80 square meters and a perimeter of 36 meters. What are the dimensions of the kitchen?
Answers
Answer:
Step-by-step explanation
Frist, the area = ab = 30 m^2 and the perimeter = 2(a + b) = 34 m or a + b = 17 m (2). Solving (1) and (2), a = 15 m and b = 2 m. Since it is a rectangle, the dimensions are (all in m) so the answer is: 15, 2, 15, 2.
Answer:
THe kitchen is 8 by 10
Step-by-step explanation:
x = width
y = length
Area = xy = 80 m²
Perimeter = 2x + 2y = 36 m
2x = 36 - 2y
x = 18 - y substitute into equation 1
(18 - y)(y) = 80
-y² + 18y - 80 = 0 find roots of y by factoring
y² - 18y + 80 = 0
(y - 8)(y - 10) = 0
y = 8, 10
Since xy = 80, then:
x = 80/10 = 8, or, x = 80/8 = 10
Now you have your dimensions: 8 and 10
To check the answers:
8 x 10 = 80 m²
2(8) + 2 (10) = 36 m
Answers are correct!
Consider the points below. P(θ),−4,0),Q(5,1,−2),R(6,4,1) (a) Find a nonzero vector orthogonal to the plane through the points P,Q, and R. (b) Find the area of the triangle PQR.
Answers
(a) A nonzero vector orthogonal to the plane through the points P, Q, and R is (9, -17, 35). (b) The area of triangle PQR is \(\sqrt\)(811) / 2.
(a) To determine a nonzero vector orthogonal to the plane through the points P, Q, and R, we can first find two vectors in the plane and then take their cross product. Taking vectors PQ and PR, we have:
PQ = Q - P = (5, 1, -2) - (-4, 0, 0) = (9, 1, -2)
PR = R - P = (6, 4, 1) - (-4, 0, 0) = (10, 4, 1)
Taking the cross product of PQ and PR, we have:
n = PQ x PR = (9, 1, -2) x (10, 4, 1)
Evaluating the cross product gives n = (9, -17, 35). Therefore, (9, -17, 35) is a nonzero vector orthogonal to the plane through points P, Q, and R.
(b) To determine the area of triangle PQR, we can use the magnitude of the cross product of vectors PQ and PR divided by 2. The magnitude of the cross product is given by:
|n| = \(\sqrt\)((9)^2 + (-17)^2 + (35)^2)
Evaluating the magnitude gives |n| = \(\sqrt\)(811).
The area of triangle PQR is then:
Area = |n| / 2 = \(\sqrt\)(811) / 2.
To know more about nonzero vector refer here:
https://brainly.com/question/32673773#
#SPJ11
Please help me step by step how to solve this quadratic equation 2a^2=-6+8a
Answers
The quadratic equation 2a^2 = -6 + 8a has two solutions: a = 3 and a = 1.
To solve the quadratic equation 2a^2 = -6 + 8a, we need to rearrange it into standard quadratic form, which is ax^2 + bx + c = 0, where a, b, and c are coefficients.
Step 1: Move all the terms to one side of the equation to set it equal to zero:
2a^2 - 8a + 6 = 0
Step 2: The equation is now in standard quadratic form, so we can apply the quadratic formula to find the solutions for 'a':
a = (-b ± √(b^2 - 4ac))/(2a)
Comparing with our equation, we have:
a = (-(-8) ± √((-8)^2 - 4(2)(6)))/(2(2))
Simplifying further:
a = (8 ± √(64 - 48))/(4)
a = (8 ± √16)/(4)
a = (8 ± 4)/(4)
Now, we can calculate the two possible solutions:
a1 = (8 + 4)/(4) = 12/4 = 3
a2 = (8 - 4)/(4) = 4/4 = 1
Therefore, the quadratic equation 2a^2 = -6 + 8a has two solutions: a = 3 and a = 1.
For more question on quadratic visit:
https://brainly.com/question/1214333
#SPJ8
What are all the pairs of twin primes between 25 and 55?
Answers
How would the fraction 5/1-sort 3. Be written if it’s denominator is rationalized using difference of squares?

Answers
Answer:
\( - \frac{5 + 5 \sqrt{3} }{2} \)
Option A is the correct option.
Solution,
Multiply and divide by its conjugate.
\( \frac{5}{1 - \sqrt{3} } \times \frac{1 + \sqrt{3} }{1 + \sqrt{3} } \\ = \frac{5(1 + \sqrt{3)} }{(1 - \sqrt{3} )(1 + \sqrt{3)} } \\ = \frac{5 + 5 \sqrt{3} }{ {(1)}^{2} - { (\sqrt{3}) }^{2} } \\ = \frac{5 + 5 \sqrt{3} }{1 - 3} \\ = \frac{5 + 5 \sqrt{3} }{ - 2} \\ = - \frac{5 + 5 \sqrt{3} }{2} \)
hope this helps...
Good luck on your assignment..
Roberto Clemente, born in Puerto Rico, became the first Latino baseball player to be inducted in the National Baseball Hall of Fame in 1973. He held many records including reaching 3,000 career hits. During that game, the umpire briefly stopped the game to give the ball to Clemente, who tossed it from second base to the first base coach. If the first base coach was standing 3 feet behind first base and Clemente was standing on second base, which is 90 feet from first base, which expression describes the distance between Clemente and the first base coach?
Answers
Answer:
93ftStep-by-step explanation:
Kindly find a simple sketch of a baseball pitch, the circle with a dot inside represents the first base coach(don't mind my drawing please I will improve).
So, from the diagram, we can see that the expression that describes the distance and the first base coach is
y=90+3
y=93
so the distance between Roberto Clemente and the first base coach is 93ft

Quadrilateral ABCD has vertices A(−2,1), B(4,4), C(5,0), and D(−1,−2).
Which side is the longest
A.BC
B.CD
C.DA
D.AB
Answers
Step-by-step explanation:
Refer to the attachment ♪♪

Using the distance formula, \(\sqrt{(y_2 - y_1)^2 + (x_2 - x_1)^2}\) to find the length of each sides, the longest side is about 6.71 units which is: d. AB
To find the longest side, we would apply the distance formula to find the length of each side.
Given:
A(−2,1)B(4,4)C(5,0)D(−1,−2)Distance formula = \(\sqrt{(y_2 - y_1)^2 + (x_2 - x_1)^2}\)
Length of AB:
Let,\(A(-2,1) = (x_1, y_1)\\\\B(4,4) = (x_2, y_2)\)
Substitute\(AB = \sqrt{(4 - 1)^2 + (4 - (-2))^2}\\\\AB = \sqrt{9 + 36}\\\\AB = \sqrt{45} \\\\AB = 6.71\)
Length of BC:
Let,\(B(4,4) = (x_1, y_1)\\\\C(5,0) = (x_2, y_2)\)
Substitute\(BC= \sqrt{(0-4)^2 + (5-4)^2}\\\\BC = \sqrt{16 + 1}\\\\BC = \sqrt{17} \\\\BC =4.12\)
Length of CD:
Let,\(C(5,0) = (x_1, y_1)\\\\ D(-1,-2) = (x_2, y_2)\)
Substitute\(CD = \sqrt{(-2 - 0)^2 + (-1 - 5)^2}\\\\CD = \sqrt{4 + 36}\\\\CD = \sqrt{40} \\\\CD =6.32\)
Length of DA:
Let,\(D(-1,-2) = (x_1, y_1)\\\\ A(-2,1) = (x_2, y_2)\)
Substitute\(DA = \sqrt{(-2 - 1)^2 + (-1 - (-2))^2}\\\\DA= \sqrt{9 + 1}\\\\DA = \sqrt{10} \\\\DA = 3.16\)
Therefore, the using the distance formula, \(\sqrt{(y_2 - y_1)^2 + (x_2 - x_1)^2}\) to find the length of each sides, the longest side is about 6.71 units which is: d. AB
Learn more here:
https://brainly.com/question/19799445
Calculate the interest on a 90-day, 9% note for $50,000 (Use a 360 day year to compute interest Round your answer to the nearest dollar ) A. S375 B. S4.500 O C. $1,125 O D. $2,250
Answers
The correct answer is C. $11,250.
To calculate the interest on a 90-day, 9% note for $50,000, we can use the simple interest formula:
Interest = Principal × Rate × Time
Given:
Principal (P) = $50,000
Rate (R) = 9% = 0.09 (decimal)
Time (T) = 90 days
Since the interest is calculated based on a 360-day year, we need to convert the time in days to a fraction of a year:
Time (T) = 90 days / 360 days = 0.25 (fraction of a year)
Now we can calculate the interest:
Interest = $50,000 × 0.09 × 0.25
Interest = $11,250
Rounded to the nearest dollar, the interest on the 90-day, 9% note for $50,000 is $11,250.
Therefore, the correct answer is C. $11,250.
To know more about simple interest:
https://brainly.com/question/30964674
#SPJ11
on any given roll of both dice, what is the probability that the number showing on die a will be greater than the number on die b? what is the probability that the number showing on die b will be greater?
Answers
The probability that the number showing on die B will be greater than the number on die A is also 5/12 or approximately 0.417.
The outcomes of rolling two dice can be represented by a table of all possible combinations of numbers on the two dice. There are 36 possible outcomes in total, since each of the six faces of the first die can be paired with any of the six faces of the second die.
To find the probability that the number showing on die A will be greater than the number on die B, we can count the number of outcomes where this is true and divide by the total number of outcomes. There are 15 outcomes where the number on die A is greater than the number on die B, as shown in the table below:
| Die A | Die B |
|-------|-------|
| 2 | 1 |
| 3 | 1 |
| 4 | 1 |
| 3 | 2 |
| 4 | 2 |
| 5 | 1 |
| 5 | 2 |
| 4 | 3 |
| 5 | 3 |
| 6 | 1 |
| 6 | 2 |
| 5 | 4 |
| 6 | 3 |
| 6 | 4 |
| 6 | 5 |
Therefore, the probability that the number showing on die A will be greater than the number on die B is 15/36, which simplifies to 5/12 or approximately 0.417.
Similarly, we can count the number of outcomes where the number on die B is greater than the number on die A. There are also 15 such outcomes, as shown in the table above. Therefore, the probability that the number showing on die B will be greater than the number on die A is also 5/12 or approximately 0.417.
Visit to know more about Probability:-
brainly.com/question/13604758
#SPJ11
I need a fast answer !! A bag has 7 blue marbles and 3 red marbles. What is the probability of drawing two red marbles, if the first marble is replaced after it is drawn? A. 1/7 B. 1/3 C. 3/10 D. 9/100
Answers
Answer:
Step-by-step explanation:
9/100 i believe as you would multiply 3/10 by 3/10 due to the fact the marble is being replaced so the probability of getting a red marble the second time will be more unlikely. If I'm right please thank me or give me brainly. Hope this helps :)
The probability of drawing two red marbles, if the first marble is replaced after it is drawn, is 9/100.
What is Probability?
It is a branch of mathematics that deals with the occurrence of a random event.
The probability of drawing a red marble on the first draw is 3/10, since there are 3 red marbles out of a total of 10 marbles.
Since the first marble is replaced before the second draw, the probability of drawing a red marble on the second draw is also 3/10.
To find the probability of drawing two red marbles in a row, we multiply the probabilities of the individual events, since they are independent:
P(drawing two red marbles) = P(red on first draw) × P(red on second draw)
P(drawing two red marbles) = (3/10) × (3/10)
= 9/100
Therefore, the probability of drawing two red marbles, if the first marble is replaced after it is drawn, is 9/100.
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ3
At the Beijing Olympics, Usain bolt won the 200 meter race with
a time of 19.30 seconds. (1m = 3.28ft, 1 mi = 2580ft)
a. What was his avg. speed in meters per second?
b. What was his avg. speed in mil
Answers
(A) Usain Bolt's average speed in meters per second was approximately 10.36 m/s.
(B) Usain Bolt's average speed in miles per hour was approximately 23.35 mph.
(A) Average speed = Distance / Time
Average speed = 200 meters / 19.30 seconds
Average speed = 10.36 meters per second
Therefore, Usain Bolt's average speed in meters per second was approximately 10.36 m/s.
(B) 1 mile = 2580 feet
Converting the distance from meters to miles:
Distance in miles = Distance in meters / (1 meter / 3.28 feet) / (1 mile / 5280 feet)
Distance in miles = 200 meters / 3.28 / 5280 miles
Time in hours = Time in seconds / (60 seconds / 1 minute) / (60 minutes / 1 hour)
Time in hours = 19.30 seconds / 60 / 60 hours
Average speed = Distance in miles / Time in hours
Average speed = (200 meters / 3.28 / 5280 miles) / (19.30 seconds / 60 / 60 hours)
Average speed = 23.35 miles per hour
Therefore, Usain Bolt's average speed in miles per hour was approximately 23.35 mph.
To know more about Average speed click here:
https://brainly.com/question/14870444
#SPJ4
Write an equation for each graph in a slope
Intercept form

Answers
Answer:
y=2x-3
Step-by-step explanation:
Y-intercept can be read off the graph.
Slope can be determined using the formula:
y2-y1 divided by x2-x1 (Substitute co-ordinates)
Answer:
y=2x-3
Step-by-step explanation:
y=mx+b
Where m is the slope and b is the y intercept
Slope is rise over run, the line is up 2 over 1
And the point of the line where it meets the y axis is -3. so b is -3