Answers
Related Questions
If anyone can help and could you put the work as well

Answers
So there is no slope because we have a horizontal line
Hope this helps

2y+8x=0
use the slope and y intercept form to graph the equation
Answers
Answer:
Step-by-step explanation:
2y+8x=0
Converting to y-intercept form:
2y = -8x
y = -4x
So, the slope is -4 and the y-intercept is at (0,0).
Assume that hybridization experiments are conducted with peas having the property that for offspring, there is a 0.75 probability that a pea has green pods. Assume that the offspring peas are randomly selected in groups of 24 Complete parts (a) through (c) below.
A. Find the mean AND the standard deviation for the numbers of peas with green pods in the groups of 24.
B. Use the range rule of thumb to find the values separating results that are significantly low AND significantly high
C. Is a result of 3 peas with green pods a result that is significantly low? Why or why not?
Answers
A. The mean and the standard deviation for the numbers of peas with green pods in the groups of 24 is 18 and 2.1213.
B. The values separating results that are significantly low and significantly high is 13.76 and 22.24.
C. The result of 3 peas with green pods a result is significantly low.
What is the probability?
The probability of an occurrence is a number used in science to describe how likely it is that the event will take place. In terms of percentage notation, it is expressed as a number between 0 and 1, or between 0% and 100%. The higher the likelihood, the more likely it is that the event will take place.
Here, we have
Given: Assume that hybridization experiments are conducted with peas having the property that for offspring, there is a 0.75 probability that a pea has green pods.
This is a binomial probability distribution problem.
Where n = 24 [groups of 24, total trials]
p = 0.75 [probability of success]
a) Mean = np =24×0.75 = 18
and std deviation =(np(1-p))1/2 = 2.1213
b) from a range rule of thumb; 2 std deviation values above and below the mean are significantly low AND significantly high
Hence significantly low value = mean -2×std deviation = 13.76 or lower values
Significantly high value =mean +2*std deviation = 22.24 or higher values
c) As 3 falls in significantly low values cause it is below 2 std deviations from the mean hence it is significantly low.
To learn more about the probability from the given link
https://brainly.com/question/24756209
#SPJ4
Vote you brainiest please help me

Answers
Answer:
Step-by-step explanation:
In number 1 I think they did a typo so we can just put 6 3/4. So if you know what to do go for it :D
Hope this helps :D
Answer:
1. 7 5/8 2. 1/6 3. 2 2/9
Step-by-step explanation:
For number one, convert 3/4 to eights because we cant subtract fourths from eighths. It is 6/8. 7/8 + 6/8 = 13/8 = 1 5/8 . 1 5/8 + 6 = 7 5/8.
For number 2: We 2/3 to sixths because we cant subtract sixths from thirds. 2/3 = 4/6. 5/6 - 4/6 = 1/6.
For number 3: Just subtract. 8 - 5 7/9 = 2 2/9.
I don't understand, please help me out... it's like 7:58...am...

Answers
Answer: Option E
Step-by-step explanation: You want to subtract x from both sides and add one from both sides in order to get the variables on one side.
When you do this you get 3x is greater than or equal to 3. Now divide by three on both sides. This becomes x is greater than or equal to 1. You want to find the number line with a closed circle on 1 since to represent the "or equal to" and you want it to go in the direction of left to right to represent the increase since it is "greater than".
1. A school orders 120 calculators.
The school receives a shipment containing 80%
of the order,
and 1 out of every 3 of these calculators is black.
How many black calculators has the school received
in this shipment?
a.32
b.40
c.50
d.96
Answers
Answer:
A. 32
Step-by-step explanation:
80% of 120 is 96
So 96 divided by 3 is 32, so 32 x 3 = 96
Which means 32/96 also equals 1/3
Because the school received 80% of the 120 so that then equals to 96 then I divided by 3 and got 32 so that’s why I believe that’s the right answer.
Twelve more than half of a number is equal to the number
Answers
So, twice the number (2x) is 12 greater than than the half of the number.
So the equation will be like,
2x=12+x/2
Solving this further,
2x=(24+x)/2
=> 4x=24+x
=>4x-x=24
=>3x=24
=>x=8..
So the number is "8".
Naeem weighs different salad takeout containers. The containers respectively weigh 4.5 ounces, 5.01 ounces, 5.3 ounces, 4.75 ounces, and 4.9 ounces. Which is the best whole number estimate of how much all the containers weigh together? 22 ounces 24.46 ounces 24.5 ounces 25 ounces
Answers
Answer:
25 oz.
Step-by-step explanation:
4.5+5.01+5.3+4.75+4.9=24.46
Answer:
25 oz
Step-by-step explanation:
Use the below information for questions 2a - 2b:
State Probability Return on A Return on B Return on C
Boom 0.30 0.35 0.25 0.10
Average 0.50 0.20 0.15 0.25
Bust 0.20 0.05 0.10 0.35
2a. Find the Mean and Variance of Asset A
2b. Find the Correlation coefficient of A and C
Answers
Answer to 2a: The mean of Asset A is 0.235 and the variance is 0.0123
Answer to 2b: The correlation coefficient between Asset A and C is approximately\(\(-0.670\) (Boom), \(-0.187\) (Average), \(-0.670\)\)(Bust).
2a. Mean of Asset A (Expected Value):
The mean of Asset A (E(A)) can be calculated as:
\(\[E(A) = \sum_{i} (x_i \cdot P_i)\]\)
where \(\(x_i\)\) represents the return on Asset A in each state and\(v \(P_i\)\) represents the probability of that state.
Using the given information, we have:
Boom:
\(\(E(A) = (0.35 \cdot 0.30) + (0.20 \cdot 0.50) + (0.05 \cdot 0.20) = 0.235\)\)
Average:
\(\(E(A) = (0.35 \cdot 0.30) + (0.20 \cdot 0.50) + (0.05 \cdot 0.20) = 0.235\)\)
Bust:
\(\(E(A) = (0.35 \cdot 0.30) + (0.20 \cdot 0.50) + (0.05 \cdot 0.20) = 0.235\)\)
Therefore, the mean of Asset A is\(\(E(A) = 0.235\).\)
2b. Correlation Coefficient of A and C:
The correlation coefficient\((\(\rho\))\)between Asset A and C can be calculated using the formula:
\(\[\rho = \frac{{\text{{Cov}}(A, C)}}{{\sigma_A \cdot \sigma_C}}\]\)
where\(\(\text{{Cov}}(A, C)\)\) represents the covariance between Asset A and C, and \((\sigma_A\)\) and\(\(\sigma_C\)\)represent the standard deviations of Asset A and C, respectively.
Using the given information, we have:
Boom:
\(\(\text{{Cov}}(A, C) = (0.35 - 0.235) \cdot (0.10 - 0.25) = -0.017\)\)
Average:
\(\(\text{{Cov}}(A, C) = (0.20 - 0.235) \cdot (0.15 - 0.25) = -0.005\)\)
Bust:
\(\(\text{{Cov}}(A, C) = (0.05 - 0.235) \cdot (0.35 - 0.25) = -0.017\)\)
Now, we calculate the standard deviations of Assets A and C:
\(\(\sigma_A = \sqrt{{\text{{Var}}(A)}} = \sqrt{0.0123} \approx 0.1108\)\)
\(\(\sigma_C = \sqrt{{\text{{Var}}(C)}} = \sqrt{0.0517} \approx 0.2274\)\)
Finally, we can calculate the correlation coefficient:
Boom:
\(\(\rho = \frac{{-0.017}}{{0.1108 \cdot 0.2274}} \approx -0.670\)\)
Average:
\(\(\rho = \frac{{-0.005}}{{0.1108 \cdot 0.2274}} \approx -0.187\)\)
Bust:
\(\(\rho = \frac{{-0.017}}{{0.1108 \cdot 0.2274}} \approx -0.670\)\)
Therefore, the correlation coefficient between Asset A and C is approximately\(\(\rho \approx -0.670\) (Boom), \(\rho \approx -0.187\) (Average), and \(\rho \approx -0.670\) (Bust).\)
Answer to 2a: \(The mean of Asset A is \(0.235\) and the variance is \(0.0123\.\)
Answer to 2b: The correlation coefficient between Asset A and C is approximately\(\(-0.670\) (Boom), \(-0.187\) (Average), \(-0.670\)\)(Bust).
Learn more Mean and Variance
https://brainly.com/question/31485382
#SPJ11
solve the following systems of linear equations by graphing
y=2/3x+4 and y=/x-1
Answers
Answer:
The solution to the system is (1.8, 7.6)
Step-by-step explanation:
To solve the system of linear equations by graphing, we need to plot the two lines on the same coordinate plane and find the point where they intersect, which will be the solution of the system.
Plot the lines:
y = 2/3x + 4 can be written as y = (2/3)x + 4, where the slope is 2/3 and the y-intercept is 4.
y = -x + 1 can be written as y = -x + 1, where the slope is -1 and the y-intercept is 1.
Find the intersection point:
To find the intersection point, we can substitute the x-value from one equation into the other equation. Let's use y = 2/3x + 4.
Substitute x from y = 2/3x + 4 into y = -x + 1:
-x + 1 = 2/3x + 4
Multiplying both sides by -3, we get:
3x - 3 = -2x - 12
Adding 2x to both sides, we get:
5x - 3 = -12
Adding 12 to both sides, we get:
5x = 9
Dividing both sides by 5, we get:
x = 1.8
Now that we have x, we can substitute it back into either equation to find the corresponding y-value. Let's use y = 2/3x + 4:
y = 2/3x + 4
y = 2/3 * 1.8 + 4
y = 3.6 + 4
y = 7.6
So the solution to the system is (1.8, 7.6), which is the point where the two lines intersect.
The average age of family of six is 25 years.the average age of four children is 15 years.if the father is 2 years older than the mother,calculate the age of the mother?
Answers
Answer:
44 years old
Step-by-step explanation:
Average age of the family =25*6=150
Average age of children=4*15=60
Average age of mother &father=150-60=90
If Mother is x then
x+(2+x)=90
2x+2=90
x=90-2/2=44
Find the amount due on a merchandise listed at 2,080 pesos, less discounts of 14% and 6%.
Answers
The total amount is given by 2080 pesos.
At discounts of 14% , the discount amount will be
So amount due due to 14%
\(2080\times\frac{14}{100}=20.8\times14=291.2\)So the amount due due to 14% discount is
\(2080-291.2=1788.8\text{Pesos}\)Now at 6% discount we have
\(2080\times\frac{6}{100}=20.8\times6=124.8\)And abount due will be
\(2080-124.8=1955.2\text{pesos}\)4. Determine the stability of the following systems with the characteristic equations. (a) 12s^5 + 4s^4 +6s^3 +2s^2 +6s + 4 = 0 (6 marks) (b) 12s^5 +8s^4 + 18s^3 + 12s^2 +9s + 6 = 0 (6 marks)
Answers
There are no sign changes in the first column of the Routh array, therefore the system is stable.
Given: Characteristic equation for system `(a)`: 12s⁵ + 4s⁴ + 6s³ + 2s² + 6s + 4 = 0
Characteristic equation for system `(b)`: 12s⁵ + 8s⁴ + 18s³ + 12s² + 9s + 6 = 0
To determine the stability of the systems with the given characteristic equations, we need to find out the roots of the given polynomial equations and check their stability using Routh-Hurwitz criteria.
To find out the stability of the system with given characteristic equation, we have to check the conditions of Routh-Hurwitz criteria.
Let's discuss these conditions:1. For the system to be stable, the coefficient of the first column of the Routh array must be greater than 0.2.
The number of sign changes in the first column of the Routh array represents the number of roots of the characteristic equation in the right-half of the s-plane.
This should be equal to zero for the system to be stable.
There should be no row in the Routh array which has all elements as zero.
If any such row exists, then the system is either unstable or marginally stable.
(a) Let's calculate Routh-Hurwitz array for the polynomial `12s⁵ + 4s⁴ + 6s³ + 2s² + 6s + 4 = 0`0: 12 6 42: 4 2.66733: 5.6667 2.22224: 2.2963.5 0.48149
Since, there are 2 sign changes in the first column of the Routh array, therefore the system is unstable.
(b) Let's calculate Routh-Hurwitz array for the polynomial `12s⁵ + 8s⁴ + 18s³ + 12s² + 9s + 6 = 0`0: 12 18 62: 8 12 03: 5.3333 0 04: 2 0 05: 6 0 0
Since there are no sign changes in the first column of the Routh array, therefore the system is stable.
Learn more about Routh array
brainly.com/question/31966031
#SPJ11
what is the l.c.m of x and y if x is the first odd prime number and y is the only even prime number?
Answers
The least common multiple (LCM) of x and y, where x is the first odd prime number and y is the only even prime number, is found out to be 6.
The first odd prime number is 3, and the only even prime number is 2. To find the LCM of 3 and 2, we consider the prime factorization of each number. The prime factorization of 3 is 3, and the prime factorization of 2 is 2.
To find the LCM, we take the highest power of each prime factor that appears in either number. In this case, there are no common prime factors between 3 and 2, so the LCM is simply the product of the two numbers: LCM(3, 2) = 3 * 2 = 6.
Learn more about prime numbers here: brainly.com/question/30210177
#SPJ11
You are designing a rectangular swimming pool that is to be sent into the ground. The width of the pool is 5 feet more than the depth, and the length is 35 feet more than the depth. The pond holds 2000 cubic feet of water, What are the dimensions of the pool?
Answers
Answer: depth = 5 ft
width = 10 ft
length = 40 ft
Step-by-step explanation:
d = depth
width = d + 5
length = d + 36
Volume = length x width x depth = 2000 cf
d(d+35)(d+5) = 2000
d(\(d^{2}\) + 40d + 175) = 2000
d^3 + 40d^2 + 175d = 2000
rewrite in standard cubic polynomial form : ax3 + bx2 + cx + d = 0
d^3 + 40(d^2) + 175d - 2000 = 0
Find the roots of the cubic polynomial:
factors of 2000 are 1, 5, 10 15, 20, etc.
Try the factor 5 first by plugging it in the equation:
5^3 + 40(5^2) + 175(5) - 2000 = 0
Lucky break! No need to find the other roots because they will be negative, and you can't have a negative value for a pool depth.
So, depth = 5 ft
width = 5 + 5 = 10 ft
length = 5 + 35 = 40 ft
I need help I will be very grateful if someone helped me
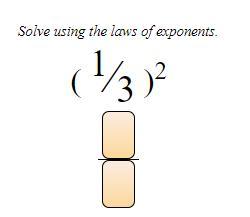
Answers
Answer:
1/3 is 0.33-0.33 ×0.33= 0.189
Step-by-step explanation:
u know what is one over three then the exponent is 2 so u multiply the number but itself as much as the exponent number is
Solve the following:
2(x+3)=x-4
Separate question
4(5x-2)=2(9x3)
Answers
Answer:
Step-by-step explanation:
2x+6=x-4
x=-10
20x-8x=.....
g How many ways are arrange the letters in UNIVERSALLY so that no two vowels occur consecutively and also the consonants appear in alphabetical order
Answers
There are 43,200 number of ways to arrange the letters in UNIVERSALLY so that no two vowels occur consecutively and the consonants appear in alphabetical order.
To find the number of ways to arrange the letters in UNIVERSALLY so that no two vowels occur consecutively and the consonants appear in alphabetical order, follow these steps:
1. Identify the vowels and consonants: Vowels are U, I, E, A, and Y; consonants are N, R, S, S, L, and L.
2. Arrange the consonants in alphabetical order: L, L, N, R, S, S.
3. Count the number of positions available for placing the vowels: There are 7 positions available for the vowels (between the consonants and at the beginning and the end of the word), which are _ L _ L _ N _ R _ S _ S _.
4. Count the permutations of the vowels: There are 5 vowels with the letters U, I, E, A, and Y occurring once. So there are 5! = 120 permutations.
5. Consider the consonants with repeating letters: Since there are two Ls and two Ss, we must divide the total permutations by the product of the repetitions (2! for L and 2! for S). Therefore, there are 6!/(2!*2!) = 360 arrangements for consonants.
6. Combine the permutations of vowels and consonants: To find the total number of ways to arrange the letters, multiply the permutations of vowels (120) by the arrangements for consonants (360).
120 * 360 = 43,200
So, there are 43,200 ways to arrange the letters in UNIVERSALLY so that no two vowels occur consecutively and the consonants appear in alphabetical order.
To learn more about number of ways, refer here:
https://brainly.com/question/29110744#
#SPJ11
What is the volume of the following triangular prism?
252 yd
126 yd
42 yd

Answers
Answer:
V = 126 yd3
Step-by-step explanation:
The base: \(\frac{(9)(4)}{2} =\frac{36}{2} =18\)
The volume: \(v=(18)(7)=126yd^{3}\)
Hope this helps
Imagine buying a brand new Ford Fusion hybrid. If x represents the number of miles a car is driven, and y represents the total amount of money spent on the car, write an equation that relates x and y for the Fusion hybrid.
Answers
The equation that relates x and y for the Fusion hybrid is y = k + x
How to write and solve equation?Total amount of money spent on the car = yNumber of miles a car is driven = xAssume, other money spent on the car = kSo,
y = k + x
Therefore, the equation that relates x and y for the Fusion hybrid is y = k + x
Learn more about equation:
https://brainly.com/question/2972832
#SPJ1
The cost to make each T-shirt is $10. You estimate that you will
sell 50 shirts. If you want to make a profit of at least $250, what
price will you charge for these T-shirts? Show your solution in two
different ways.
Answers
The price per T-shirt should be at least $15 to achieve a profit of $250.
To calculate the price per T-shirt that will yield a profit of at least $250, we need to consider the cost of production, the desired profit, and the number of shirts to be sold.
Given that the cost to make each T-shirt is $10, and we want to sell 50 shirts, the total cost of production would be 10 * 50 = $500.
Now, let's calculate the minimum revenue needed to achieve a profit of $250. We add the desired profit to the total cost of production: $500 + $250 = $750.
Finally, to determine the price per T-shirt, we divide the total revenue by the number of shirts: $750 ÷ 50 = $15.
Therefore, to make a profit of at least $250, the price per T-shirt should be set at $15.
By selling each T-shirt for $15, the total revenue would be $15 * 50 = $750. From this revenue, we subtract the total production cost of $500 to calculate the profit, which amounts to $750 - $500 = $250. Thus, by charging $15 per T-shirt, the desired profit of $250 is achieved.
For more question on profit visit:
https://brainly.com/question/30495119
#SPJ8
Find the area of the largest rectangle having two vertices on the x axis and two more vertices above the x axis and on the parabola with equation y=9-x²?
Answers
The area of the largest rectangle having two vertices on the x-axis and two more vertices above the x-axis and on the parabola with equation y = 9 - x² is 36 square units.
To find the area of the largest rectangle having two vertices on the x-axis and two more vertices above the x-axis and on the parabola with equation y = 9 - x², we need to use optimization techniques.
Let's start by drawing the graph of the parabola and the rectangle:
|
9 -| ************
| **** ****
| *** ***
| ** **
| * *
| * *
| ** **
*------------------*------------------*
x = -3 x = 0 x = 3
Let's call the height of the rectangle h and the width 2x (since we have two vertices on the x-axis). The area of the rectangle is then A = 2xh. To find the maximum area, we need to maximize A with respect to x and h.
The two vertices above the x-axis are on the parabola y = 9 - x², so their coordinates are (x, 9 - x²) and (-x, 9 - x²). The height of the rectangle is therefore h = 9 - x². The width of the rectangle is 2x.
The area of the rectangle is therefore A = 2xh = 2x(9 - x²). To find the maximum area, we need to find the critical points of A(x).
Taking the derivative of A(x) with respect to x, we get:
A'(x) = 18x - 2x³
Setting A'(x) = 0, we get:
0 = 2x(9 - x²)
This gives us two critical points: x = 0 and x = ±√9 = ±3.
To find the maximum area, we need to check which of these critical points give us the maximum value of A(x). We can do this by computing the value of A(x) at each critical point:
A(0) = 2(0)(9 - 0²) = 0
A(3) = 2(3)(9 - 3²) = 36
A(-3) = 2(-3)(9 - (-3)²) = 36
Therefore, the maximum area is obtained when x = ±3, and the area of the rectangle is A = 2x(9 - x²) = 36.
In summary, the area of the largest rectangle having two vertices on the x-axis and two more vertices above the x-axis and on the parabola with equation y = 9 - x² is 36 square units.
Know more about "parabola" here:-
https://brainly.com/question/29322662#
#SPJ11
Mario worked from 8:25 to 12:45 yesterday.Today he will work 11:20 to 3:10. How many hours did he work in all?
Answers
Answer:
Mario worked from
8:25 to 12:45 yesterday
11:20 to 3:10 today
To find the total time of work
12:45
-8:25
_____
4:20
again
11:20
-3:10
______
8:10
Therefore
4:20 + 8:20 = 12 hours 30 min
The total hours to work in all will be;
⇒ 12 hours 30 minutes
What is Addition?A process of combining two or more numbers is called addition.
Given that;
Mario worked from 8:25 to 12:45 yesterday.
And, Today he will work 11:20 to 3:10.
Now,
Since, Mario worked from 8:25 to 12:45 yesterday.
Hence, The number of hours to work yesterday = 12 : 45 - 8 : 25
= 4 : 20
And, Today he will work 11:20 to 3:10.
Hence, The number of hours to work today = 11 : 20 - 3 : 10
= 8 : 10
Thus, The total hours to work = 4 : 20 + 8 : 10
= 12 : 30
= 12 hours 30 minutes
Learn more about the addition visit:
https://brainly.com/question/25421984
#SPJ2
Tori wa hopping for a new dre for her chool' pring dance. She pent $40 on the dre he picked, but he had expected to pend 50% more than that. How much had Tori expected to pend?
Answers
The total amount that Tori had expected to spend is therefore $40 + $20 = $60.
To find out how much Tori had expected to spend on the dress, we need to calculate the amount that she expected to spend in addition to the $40 she actually spent. The problem states that she expected to spend 50% more than $40 on the dress. 50% is the same as 0.50, so we can multiply $40 by 0.50 to find the additional amount that Tori expected to spend. This comes out to be $20. To find the total amount that Tori had expected to spend, we need to add this additional amount to the $40 she actually spent. The total amount that Tori had expected to spend is therefore $40 + $20 = $60.
To learn more about multiply, visit:
brainly.com/question/23536361
#SPJ4
What is the MAD for these numbers? 5 22 14 13 18 7 9 12
Answers
Answer:
4.25
Step-by-step explanation:
Can anyone help me with this question please tell me if it is right or wrong
2/3 and 4/5
Answers
2/3 is not greater than 4/5. Rather 4/5 is greater than 2/3.
To find which fractional number is greater than other we need to compare them. To compare two fractional numbers we to make their denominators same. We can do that by taking LCM.
LCM stands for "least common multiple". It is a mathematical concept used to find the smallest positive number divisible by two or more given numbers.
LCM of 3 and 5 is 15
2/3 will change into 10/15, as we multiply 5 with both numerator and denominator.
4/5 will change into 12/15, as we multiply 3 with both numerator and denominator.
In 10/15 and 12/15 we will compare numerator as denominator is same now.
by comparing, we get:
12/15 > 10/15
So, 4/5 > 2/5
Therefore , 2/3 is not greater than 4/5.
To learn more about comparison:
https://brainly.com/question/15193212?referrer=searchResults
The correct question is -
"2/3 is greater than 4/5, right or wrong?"
A rectangle is inscribed in a parabola y^2 = 16x with the side of the rectangle along the latus rectum of the parabola. If the area of the rectangle is maximized, compute its perimeter.
a. 24.63
b. 13.69
c. 14.57
d. 20.69
Answers
The perimeter of the rectangle, when the area is maximized, is approximately 24.63 units. Therefore, correct option is a.
To maximize the area of the rectangle inscribed in the parabola \(y^2 = 16x\), we need to find the dimensions of the rectangle. Since the side of the rectangle is along the latus rectum of the parabola, we know that the length of the rectangle is equal to the latus rectum.
The latus rectum of the parabola \(y^2 = 16x\) is given by the formula 4a, where "a" is the distance from the focus to the vertex of the parabola. In this case, the focus is located at (4a, 0).
To find "a," we can equate the equation of the parabola to the general equation of a parabola in vertex form: \(y^2 = 4a(x - h)\), where (h, k) is the vertex of the parabola.
Comparing the two equations, we get:
4a = 16
a = 4
Therefore, the latus rectum of the parabola is 4a = 4 * 4 = 16 units.
Since the length of the rectangle is equal to the latus rectum, we have length = 16 units.
Now, to find the width of the rectangle, we need to determine the corresponding y-coordinate on the parabola for the given x-coordinate of the latus rectum. The x-coordinate of the latus rectum is half the length, which is 16/2 = 8 units.
Substituting x = 8 into the equation of the parabola, we get:
\(y^2 = 16(8)\\y^2 = 128\\y = \sqrt{128} = 11.31\)
Therefore, the width of the rectangle is approximately 11.31 units.
The perimeter of the rectangle is given by the formula:
Perimeter = 2(length + width)
Plugging in the values, we have:
Perimeter = 2(16 + 11.31)
Perimeter ≈ 2(27.31)
Perimeter ≈ 54.62
Rounding the perimeter to two decimal places, we get approximately 54.62 units, which is equivalent to 24.63 units.
To know more about Area, visit
https://brainly.com/question/25292087
#SPJ11
Angels 1 and 2 are congruent because they are?A. Verification linesB. Corresponding angles C. Alternate interior anglesD. Alternate exterior angels

Answers
In the given image we are asked to determine why angles 1 and 2 are congruent. This can be seen below.
Explanation
In geometry, corresponding angles are formed where a line known as an intersecting transversal, crosses through a pair of straight lines. Corresponding angles are the pairs of angles that are found in the same relative position on different intersections.
Notice that angles 1 and 2 obey the above rule. Therefore;
Answer: Option B
A coefficient is...
Answers
Answer:
a numerical or constant quantity placed before and multiplying the variable in an algebraic expression
Match each linear equation to its slope and y-intercept.
slope:2, y-intercept:
-3+5y = 4
slope:2, y-intercept: 2
5y-1 =15
slope:$, y-intercept:
2y-3.1 = 7
slope:6, y-intercept: 3
2y=5T+7
slope:-5, y-intercept: 5

Answers
Answer:
-x + 5y = 4
5y = x + 4
y = x/5 + 4/5
Slope: 1/5
Y-intercept: 4/5
5y - x = 15
5y = x + 15
y = x/5 + 3
Slope: 1/5
Y-intercept: 3
2y - 3x = 7
2y = 3x + 7
y = 3/2x + 7/2
Slope: 3/2
Y-intercept: 7/2
2y = 5x + 7
y = 5/2x + 7/2
Slope: 5/2
Y-intercept: 7/2
