Lisa is cooking muffins, the recipe calls for 7 cups of sugar. She has already put in 2 cups. How many more cups does she need to put in? I need this in a equation.
Answers
Answer:
5 more cups.
7- 2 = 5
Step-by-step explanation:
Hope this helps!
Answer:
7-2=? ?=5
2+?=7 ?=5
7-?=2 ?=5
Step-by-step explanation:
Any of the examples I gave will work.
Related Questions
Question 1 options:
In the diagram, ∆UVW~∆XYW. Use similarity criteria for triangles to determine the height of the tree. Then fill in the blank:
h = _____ ft (Answer with numbers only.)

Answers
Answer:
Step-by-step explanation:
In similar triangles, corresponding parts are in same ratio.
\(\dfrac{h}{40}=\dfrac{5}{8}\\\\\\h=\dfrac{5}{8}*40\\\\\\ = 5*5\\\\h = 25 \ ft\)
Mrs. Wright is planning her best friend's baby shower. She calculates that the food will cost $9 per guest, and she has already spent $43 on decorations.
Answers
Based on the questions, 13 guests are attending her best friend’s baby shower.
How did we get 13 guests as a result?Firstly, we need to write down the numbers that are already stated in the question.
The food will cost around $9 per guests. She spent $43 on decoration for the event. Then, she can afford to spend $160 for the event.43 + 9 × х = 160
Secondly, move the x to continue counting.
9x = 160 – 43
Thirdly, calculate the numbers above.
9x = 117
Then, move the X to get the answer.
X = \(\frac{117}{9}\)
Lastly, try to finish the division.
X = 13
In conclusion, the result shows that 13 guests attend Mrs. Wright’s best friend's baby shower.
The above question is about the algebraic word problem.
A word problem is a math question written in a short story scenario. Usually, it is a simple short story that is easy to understand.
Learn more about Algebra word problem:
https://brainly.com/question/21405634
#SPJ4
the national center for health statistics (nchs) reports that 70% of u.s adults aged 65 and over have ever recieved a penumococcal vaccination. assume that the pneumococcal vaccination rate applies to an independent random sample of 20 u.s adults aged 65 and over who visit an emergency room (er). compute the probability that exactly 14 adults have been vaccinated. round your answer to three decimal places.
Answers
The probability that exactly 14 adults have been vaccinated 0.49
Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty. We can predict only the chance of an event to occur i.e., how likely they are going to happen, using it. Probability can range from 0 to 1, where 0 means the event to be an impossible one and 1 indicates a certain event
the national center for health statistics (nchs) reports that 70% of us adults aged 65 and over have ever vaccination
the pneumococcal vaccination rate applies to an independent random sample of 20 us adults aged 65
the probability that exactly 14 adults have been vaccinated
(14/20)*(70/100)
0.49
The probability that exactly 14 adults have been vaccinated 0.49
To know more about probability visit brainly.com/question/30034780
#SPJ4
pls explain how to do this!!!!

Answers
Answer:
h ≈ 29.98
Step-by-step explanation:
diameter = 12m
volume = \(1130m^{3}\)
radius = 6m
The equation to find the height given radius and volume:
\(h = \frac{3(V)}{\pi r^2}\)
Plug in values

Answer:
Given:-
Diameter=12m
Volume=1130m³
Takeπ=3.14
To find:-
Height of cone=?
Step-by-step explanation:
Solution:-
Radius=d/2
= 12/2
=6m
Volume of cone=1/3πr²h
h= 3v/πr²
= 3×1130/3.14× 6²
= 3390/113.04
= 29.98m
hence, the height of cone is 30m.
A grocery store sold 30% of its pears and had 455 pears remaining. How many pears did the grocery store start with
Answers
To find the initial number of pears at the grocery store, you need to consider that 455 pears represent 70% (100% - 30%) of the total number of pears. The grocery store started with 1517 pears.
We know that the grocery store sold 30% of its pears, which means they have 70% of the pears remaining. We can use a proportion to figure out how many pears they started with:
30/100 = x/total pears
We can simplify this to:
0.3 = x/total pears
Now we need to solve for total pears. We can start by cross-multiplying:
0.3 * total pears = x
Next, we can substitute the information we were given:
0.3 * total pears = 455
Now we can solve for total pears:
total pears = 455 / 0.3
total pears = 1516.67 (rounded to the nearest whole number)
So the grocery store started with approximately 1517 pears.
Know more about the proportion
https://brainly.com/question/1496357
#SPJ11
the figure above shows the graph of the twice-differentiable function g and the line tangent to the graph of g at the point (0,3). the value of limx→0g(x)e−x−3x2−2x is
Answers
Using L'Hopital's rule, we can find that the limit is equal to (g(0) - 3)/2.
Since the line tangent to g at (0,3) has slope 2, we know that g(0) - 3 = 2(0) = 0. Therefore, the limit is 0/2 = 0. Based on the given information, we have a twice-differentiable function g(x) and its tangent line at the point (0,3). To find the value of the limit as x approaches 0 for g(x)e^(-x) - 3x^2 - 2x, we can use L'Hopital's rule since it involves indeterminate forms of the type 0/0 or ∞/∞. Apply L'Hopital's rule twice on the given expression. Then, evaluate the resulting expression at x=0. This will give you the value of the limit for the given expression. Make sure to check if the conditions for using L'Hopital's rule are met before applying it.
To know more about tangent visit:
https://brainly.com/question/10053881
#SPJ11
Builtrite has calculated the average cash flow to be $14,000 with a standard deviation of $5000. What is the probability of a cash flow being between than $16,000 and $19,000 ? (Assume a normal distribution.) 16.25% 18.13% 23.90% 2120%
Answers
The correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.
We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.
The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.
First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.
z1 = 2,000 / 5,000 = 0.4.
Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.
z2 = 5,000 / 5,000 = 1.
Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.
Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.
Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.
Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.
So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To learn more about probability click here:
brainly.com/question/31828911
#SPJ11
The probability of a cash flow between $16,000 and $19,000 is approximately 18.59%.
To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.
We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.
The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.
First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.
z1 = 2,000 / 5,000 = 0.4.
Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.
z2 = 5,000 / 5,000 = 1.
Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.
Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.
Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.
Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.
So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To learn more about probability click here:
brainly.com/question/31828911
#SPJ11
A periodic signal f(t) has a period T0. Write the relationship between f(t) and T0. (b) An amplitude modulated signal x(t) can be represented by x(t)=A[1+cos(ω0t)]cos(ωct), where A and ω0 are constants. (i) Show that the signal is a periodic signal. (ii) Using the definition of the period of a periodic signal, find the period of the signal. (c) Above signal x(t) can be represented as a summation of waveforms x(t)=∑n=0[infinity]Ancos(ωTt)+Bnsin(ωTt) (i) Find the value of ωT. (ii) Find the values of An and Bn for n=0,1,2,……,[infinity].
Answers
The values of An and Bn will depend on the specific amplitude modulation scheme and the values of A and ωc.
a) The relationship between a periodic signal f(t) and its period T0 is that f(t) repeats itself after every T0 units of time. In other words, for any t, f(t) = f(t + nT0) where n is an integer. The period T0 is the smallest positive value for which this condition holds.
b) (i) To show that x(t) is a periodic signal, we need to demonstrate that it repeats itself after a certain period. We can see that the term cos(ω0t) in x(t) has a period of 2π/ω0. The term cos(ωct) also has a period of 2π/ωc. Since both terms are multiplied together, the resulting signal x(t) will have a period that is a common multiple of 2π/ω0 and 2π/ωc, ensuring periodicity.
(ii) The period of the signal x(t) can be found using the definition of period for a periodic signal. We need to find the smallest positive value of T such that x(t + T) = x(t) for all t. Considering the cosine function with the smallest period, we have 2π/ω0 as a candidate for T. We also need to ensure that the term cos(ωct) does not introduce any additional periodicity. Therefore, the period of x(t) is T0 = 2π/ω0.
c) (i) The value of ωT can be found by comparing the terms in the representation of x(t). From x(t) = ∑n=0[∞]Ancos(ωTt) + Bnsin(ωTt), we can see that ωT = ωc.
(ii) To find the values of An and Bn, we can compare the coefficients of the cosine and sine terms in the representation of x(t). For n = 0, we have A0 = A and B0 = 0. For n > 0, the values of An and Bn will depend on the specific amplitude modulation scheme and the values of A and ωc.
Learn more about amplitude modulation from given link
https://brainly.com/question/10060928
#SPJ11
what is the probability that three or more defective bowing balls are found in the first 25 examined? do not do the calculation, but do write out the mathematical expression you would use to answer the question.
Answers
The probability that three or more defective bowling balls are found in the first 25 examined can be calculated using the binomial distribution formula, specifically P(X ≥ 3) = 1 - P(X < 3).
To calculate the probability that three or more defective bowling balls are found in the first 25 examined, we would use the binomial distribution formula. This formula calculates the probability of a certain number of successes (in this case, finding a defective bowling ball) in a given number of trials (25 examinations) with a known probability of success (the overall proportion of defective bowling balls).
The mathematical expression we would use is:
P(X ≥ 3) = 1 - P(X < 3)
Where X is the number of defective bowling balls found in the first 25 examinations. To calculate P(X < 3), we would use the binomial probability formula:
P(X = x) = (n choose x) * p^x * (1-p)^(n-x)
Where n is the number of trials (25), p is the probability of success (the proportion of defective bowling balls), and x is the number of successes (in this case, 0, 1, or 2).
Once we have calculated P(X < 3), we can subtract this value from 1 to find P(X ≥ 3), which is the probability of finding three or more defective bowling balls in the first 25 examinations.
For more about probability:
https://brainly.com/question/11234923
#SPJ11
Which question is a statistical question?
A How tall is the oak tree?
B How much did the tree grow in one year?
C What are the heights of the oak trees in the schoolyard?
What is the difference in height between the oak tree and the pine tree?
Answers
Answer:D
(Sorry if I’m wrong)
A company has a monthly time series that regularly shows sales being higher in the summer months. This is an example of which component?.
Answers
This is an example of a seasonal component in a time series. A seasonal component refers to regular, predictable patterns that are associated with the time of year, such as increased sales during the summer months.
What are the different components in sales?Selling products or services to clients in exchange for cash or other types of payment is known as ale. The sales process consists of a number of elements, such as:
Product: The items or services being sold are referred to here. A corporation must have a comprehensive grasp of its product offerings and how they fit the demands of its target market.
Price: The sum of money that a consumer must fork over in order to purchase the item or service. Price should be set to maximise profit while maintaining market competitiveness.
Locations where higher the good or service is sold are referred to here as "place." Physical storefronts, internet marketplaces, or a network of distributors may all fall under this category.
To learn more about different components in sales, visit:
https://brainly.com/question/14570921
#SPJ4
A shopkeeper sold an article for Birr 280. If its cost price is Birr 350 then what is his loss percentage?
Answers
Answer:
percentage loss = 20%
Step-by-step explanation:
percentage loss is calculated as
\(\frac{loss}{CP}\) × 100% ( CP is the cost price )
loss = SP - CP ( SP is selling price )
loss = CP - SP = 350 - 280 = 70 , then
percentage loss = \(\frac{70}{350}\) × 100% = 0.2 × 100% = 20%
i need the area, it is the area if composite fugures! ASAP!!

Answers
I broke it up to 2 squares and a triangle
When light bounces off a rough surface, in different directions, what is this called? (2 points)
a
Interaction
b
Movement
c
Property
d
Reflection
Answers
Simplify a/2b times bc/a
Answers
Answer:
\(\dfrac{c}{2}\)
Step-by-step explanation:
We can simplify the given expression by canceling like terms.
Remember that anything divided by itself is 1.
ex:
\(\dfrac{2x}{x} = 2 \cdot \dfrac{x}{x} = 2 \cdot 1 = 2\)
Applying this logic to the given expression:
\(\dfrac{a}{2b} \cdot \dfrac{bc}{a}\)
↓ simplify multiplication of fractions
\(\dfrac{a \cdot bc}{2b \cdot a}\)
↓ rewrite to align like variables
\(\dfrac{a \cdot b \cdot c}{a \cdot b \cdot 2}\)
↓ separate out variables that are divided by each other
\(\dfrac{a}{a} \cdot \dfrac{b}{b} \cdot \dfrac{c}{2}\)
↓ represent them as 1
\(1 \cdot 1 \cdot \dfrac{c}{2}\)
↓ rewrite without unnecessary 1's
\(\dfrac{c}{2}\)
I am trying to find the value of x, y, and z.
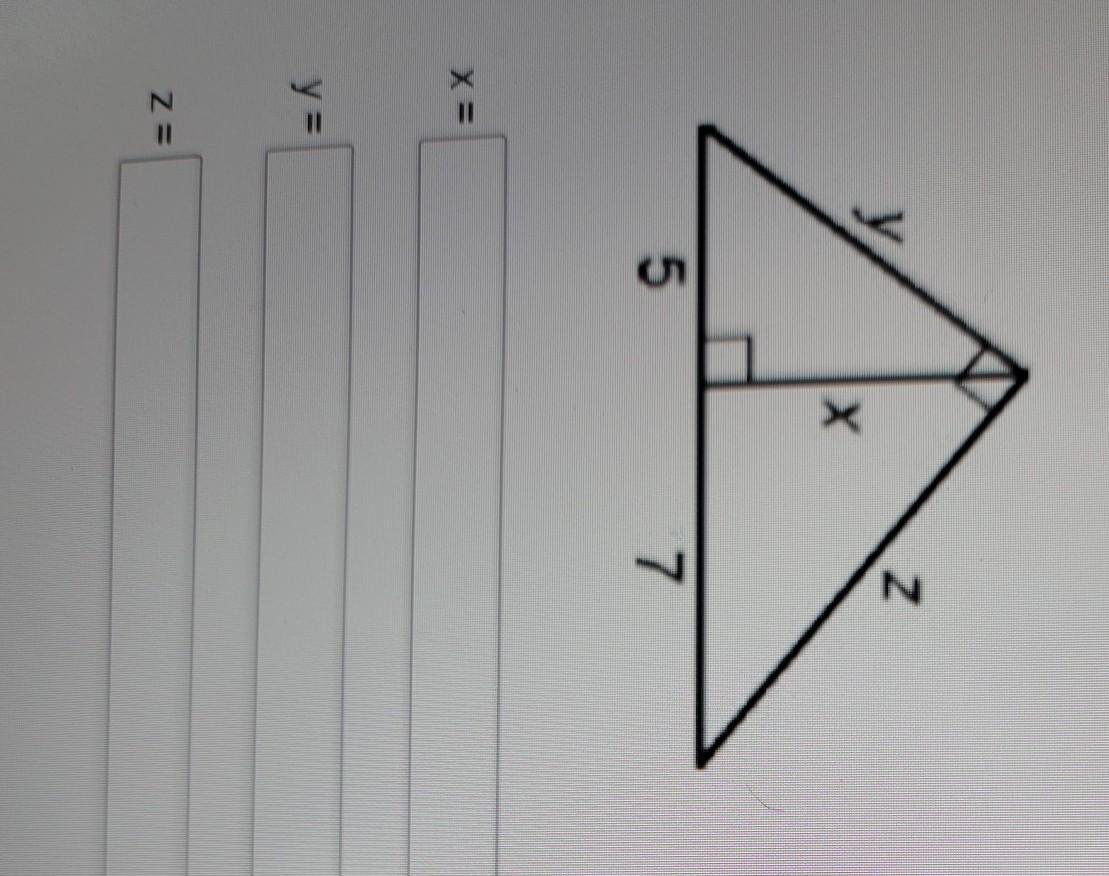
Answers
Answer:
\(\begin{gathered} x=\sqrt[]{35}=5.62 \\ y=\sqrt[]{60}=7.75 \\ z=\sqrt[]{84}=9.17 \end{gathered}\)Explanation: We need to find x y z, three missing sides:
From the given triangle, we can form three equations, using the Pythagorean theorem as:
\(\begin{gathered} (1)\rightarrow5^2+x^2=y^2 \\ (2)\rightarrow7^2+x^2=z^2 \\ (3)\rightarrow z^2+y^2=(7+5)^2=12^2 \\ \end{gathered}\)Solution by substitution:
Substituting (1) in (3) gives:
\(\begin{gathered} z^2+5^2+x^2=12^2 \\ z^2+25+x^2=144 \\ z^2+x^2=144-25=119 \\ z^2+x^2=119\rightarrow(4) \end{gathered}\)We have reached equation (4), solving for z in equation (4), and then substituting it into equation (2) gives:
\(\begin{gathered} 7^2+x^2=119-x^2\rightarrow2x^2=119-49=70 \\ \therefore\rightarrow \\ x=\sqrt[]{\frac{70}{2}}=\sqrt[]{35}=5.916 \end{gathered}\)Plugging this x into equation (4) gives:
\(\begin{gathered} z^2+(\sqrt[]{35})^2=119\rightarrow z^2=119-35=84 \\ \therefore\rightarrow \\ z=\sqrt[]{84}=9.165 \\ \\ \end{gathered}\)Now that we have x and z, we plug x it into equation (1) and we get:
\(\begin{gathered} 5^2+(\sqrt[]{35})^2=y^2 \\ \therefore\rightarrow \\ y^2=25+35=60 \\ y=\sqrt[]{60}=7.75 \end{gathered}\)x y z respectively are:
\(\begin{gathered} x=\sqrt[]{35}=5.62 \\ y=\sqrt[]{60}=7.75 \\ z=\sqrt[]{84}=9.17 \end{gathered}\)need help asap!!
Find the unknown size of the angle

Answers
Answer:
I hope this guides you!
Step-by-step explanation:
To determine to measure of the unknown angle, be sure to use the total sum of 180°. If two angles are given, add them together and then subtract from 180°. If two angles are the same and unknown, subtract the known angle from 180° and then divide by 2.
“Em uma fazenda a soma entre o número vacas e de galinhas equivale a 72 e a diferença entre o número de vacas e o triplo do número de galinhas é -88.” Quantas galinhas há na fazenda?
Answers
Answer:
There are 40 hens on the farm
Step-by-step explanation:
Here, we want to know the number of hens on the farm.
Let the number of cows be c and the number of hens be h
From the first statement in the question;
c + h = 72 •••••••••••••(i)
From the second statement ;
c - 3h = -88 •••••••••(ii)
We can then solve both equations simultaneously to get h;
That would be easier by subtracting equation ii from i
Thus, we have;
(c-c) + h-(-3h) = 72-(-88)
4h = 160
h = 160/4
h = 40
There are 40 hens on the farm
Identify any relative maximums

Answers
Answer:
Identifying any relative maximums
10,-9,1,3.7,10
Hope it's answer
mark as Brainlist and THANKS
Step-by-step explanation:
HELPPPPPPPpppppppppp

Answers
Answer:
AB = 130°
Step-by-step explanation:
The inscribed angle 65° is half the measure of its intercepted arc, then
arc AB = 2 × 65° = 130°
Geometry statements please.

Answers
It is concluded that TU ≅ UV is by the definition of congruence as shown in the solution part.
As per the given figure, the required proof would be as:
Statements:
1. U is the midpoint of SW.
2. T is the midpoint of SU.
3. V is the midpoint of UW.
4. TU || WV (by midpoint theorem)
5. TV || UW (by midpoint theorem)
6. UT = TV (by midpoint theorem)
7. UV = 2VT (by midpoint theorem)
Reasons:
1. Given.
2. Given.
3. Given.
4. Midpoint theorem.
5. Midpoint theorem.
6. Midpoint theorem.
7. Midpoint theorem.
Therefore, TU ≅ UV by the definition of congruence.
Learn more about the midpoint here :
brainly.com/question/5127660
#SPJ1
The Blackburn family has a square field where they keep their cattle. The area of the field is 40,000 ft square, and Mr. Blackburn wants to put a fence diagonally through the field. What should the length of the fence be?
Answers
If area of "square-field" is 40000 ft square, and Mr. Blackburn is putting a fence diagonally in field, then the length of fence be is 282.84 ft.
The area of the square-field is = 40000 ft²,
We equate this with area formula,
We get,
⇒ (side)² = 40000,
⇒ side = 200,
substituting the side-length as 200 ft, in the diagonal formula,
we get,
⇒ Length of diagonal of field is = (side)√2,
⇒ Length of diagonal of field is = (200)√2,
⇒ Length of diagonal of field is ≈ 282.84 ft.
Therefore, the length of the fence of the field is 282.84 ft.
Learn more about Area here
https://brainly.com/question/30578725
#SPJ1
Rewrite the equation by completing the square.
x? - 8x + 7 = 0
(x + __)^2 = 0
Answers
Answer:
(x - 4)² - 9 = 0
Step-by-step explanation:
x² - 8x + 7 = 0
To complete the square
add/subtract ( half the coefficient of the x- term)² to x² - 8x
x² + 2(- 4)x + 16 - 16 + 7 = 0
(x - 4)² - 9 = 0
Which graph displays a rate of change of 2.5?
On a coordinate plane, a line with negative slope goes through points (negative 2, 0) and (negative 1, negative 2).
On a coordinate plane, a line with negative slope goes through points (0, negative 3) and (2, 2).
On a coordinate plane, a line with positive slope goes through points (0, 1) and (2, 2).
Answers
Answer:
in edg is B
Step-by-step explanation:
Answer:
It's B
Step-by-step explanation:
Brainiest goes to the first correct answer thanks

Answers
Answer:
20
Step-by-step explanation:
we can see that there are already answers for 2 which is six 6+6=12 now we can see that a triangle look the same as the six over the 8mm so that must be six so 6+6+6=18 now there is still s little section missing over the 8mm (the half triangle half square) is missing a section we can see that the perimeter is 8 and the area is 6 and 6+2=8 so that little area is 2 so 6+6+6+2=20
Khloe made 20% of her free throws over the season. If she shot 240 free throws, how many did she make?
Answers
how many three-digit numbers can be formed from the digits 0, 1, 2, 3, 4, 5, and 6 if each digit can be used only once?
Answers
Answer:
180
Step-by-step explanation:
A 3-digit number cannot start with 0, so the leftmost digit is a choice of 6 digits out of the 7. The middle digit can be chosen from all 7 digits minus the one already used, so there are 6 choices. The right digit can be chosen from 5.
6 × 6 × 5 = .180
The number of three-digit numbers that can be formed from the digits 0, 1, 2, 3, 4, 5, and 6 is 180.
This can be calculated by finding the number of element availabe at first place which is 6 excluding 0 than for second position 6 as first number is excluded and 0 is added and for the last positon the number of possibe combination is 5 as 2 digits are already used.
The final answer is 6*6*5 = 180
so count of 3 digit numbers that can be formed by the given set of digit without repetetion allowed is 180
To know more about three-digit numbers click on below link:
https://brainly.com/question/16878161#
#SPJ11
Solve for x and y
Please help I forgot what I needed to do!

Answers
can you please answer this quick!

Answers
Answer:
a. 3*3-5
=6-5
=1
b. 3*(-2)-5
=-6-5
=-11
c. f(x)=1
or,1=3x-5
or,1+6=x
x=7
5/16 = 15/18 is proportion
Answers
Answer:
False
Step-by-step explanation:
In a proportion, the two fractions are equal. Here the denominators are different for the same numerator, so the fractions are not equal. The given expression is not a proportion.