Let X and Y be continuous random variables with joint probability density function
fX,Y (x,y) =2(x^2)y/81 , 0 ≤x ≤3, 0 ≤y ≤3
0, otherwise.
Find P(X > 3Y ) and P(X + Y > 3).
Answers
The probability that X is greater than 3Y is 1/2, and the probability that X + Y is greater than 3 is 1/8.
To find P(X > 3Y), we need to integrate the joint probability density function over the region where X is greater than 3Y. We set up the integral as follows:
P(X > 3Y) = ∫∫[2(x^2)y/81] dy dx
The integration limits are determined by the condition X > 3Y. From 0 ≤ x ≤ 3, we have 0 ≤ 3Y ≤ x, which gives us 0 ≤ Y ≤ x/3. So, the integral becomes:
P(X > 3Y) = ∫[0 to 3] ∫[0 to x/3] [2(x^2)y/81] dy dx
Simplifying the integral, we get:
P(X > 3Y) = ∫[0 to 3] [(x^2)/27] dx
Evaluating the integral, we find P(X > 3Y) = 1/2.
To find P(X + Y > 3), we integrate the joint probability density function over the region where X + Y is greater than 3. We set up the integral as follows:
P(X + Y > 3) = ∫∫[2(x^2)y/81] dx dy
The integration limits are determined by the condition X + Y > 3. From 0 ≤ y ≤ 3, we have 3 - y ≤ X ≤ 3. So, the integral becomes:
P(X + Y > 3) = ∫[0 to 3] ∫[3-y to 3] [2(x^2)y/81] dx dy
Simplifying the integral, we get:
P(X + Y > 3) = ∫[0 to 3] [2y/27] dy
Evaluating the integral, we find P(X + Y > 3) = 1/8.
Learn more about probability here: brainly.com/question/13604758
#SPJ11
Related Questions
Tanyas baked goods took in 175$ To help raise money for the chorus club .Tanya need to spend 32$ for baking supplies write and evaluate and addition expression to find how much profit tanyas baked goods make ?
Answers
Step-by-step explanation:
6 I think that is the answer I hop you get it right
One factor of the function f(x) = x3 − 9x2 + 20x − 12 is (x − 6). Describe how to find the x-intercepts and the y-intercept of the graph of f(x) without using technology. Show your work and include all intercepts in your answer.
Answers
For the given function f(x), x-intercepts are 1,2 and 6 and the y-intercept is -12
Given :
\(f(x) = x^{3} -9x^{2} +20x -12 \\\)
One of the factors of f(x) is (x-6)
Dividing f(x) by (x-6), we get :
\(\frac{x^{3} -9x^{2} +20x -12 \\}{x-6} = x^{2} -3x +2\)
Now expanding, \(x^{2} -3x +2\)
\(x^{2} -3x +2 = x^{2} -2x -x +2 =x(x-2) -(x-2) = (x-2)(x-1)\)
Hence, \(x^{3} -9x^{2} +20x -12 = (x-6)(x-1)(x-2)\)
For x-intercept, f(x) = 0 . Then
(x-6)(x-1)(x-2) =0
x = 1,2 and 6
For y-intercept, x=0 in f(x)
f(0) = -12
Hence, the x-intercepts are 1,2, and 6 and the y-intercept is -12.
To read more about intercepts, visit https://brainly.com/question/14180189
#SPJ1
For what amount of exit proceeds would these two structures yield the same amount of carried interest?
.20 (Z-250) = .30 (Z-200)
Solve for Z.
Answers
Answer:
Step-by-step explanation:"To solve this equation, you can start by distributing the 0.20 and 0.30 terms. Then, you can simplify the equation by combining like terms. After that, you can isolate the variable Z on one side of the equation by adding or subtracting terms from both sides. Finally, you can solve for Z. The solution is Z = 1000. Does that help?"
Consider the following. n = 5 measurements: 5, 3, 5, 3, 1 Calculate the sample variance, s^2, using the definition formula. s^2 = _____ Calculate the sample variance, s^2 using the computing formula. S^2 = ______ Calculate the sample standard deviation, s. (Round your answer to three decimal place )
S = _____
Answers
The sample variance using the computing formula is S² = 2.24.
The sample standard deviation is S ≈ 1.496.
How did we get the values?To calculate the sample variance, s², using the definition formula, you need to follow these steps:
1. Find the mean (average) of the measurements:
Mean (x-bar) = (5 + 3 + 5 + 3 + 1) / 5 = 17 / 5 = 3.4
2. Calculate the deviation of each measurement from the mean:
Deviation = measurement - mean
Deviation = (5 - 3.4), (3 - 3.4), (5 - 3.4), (3 - 3.4), (1 - 3.4)
= 1.6, -0.4, 1.6, -0.4, -2.4
3. Square each deviation:
Deviation squared = (1.6)², (-0.4)², (1.6)², (-0.4)², (-2.4)²
= 2.56, 0.16, 2.56, 0.16, 5.76
4. Calculate the sum of the squared deviations:
Sum of squared deviations = 2.56 + 0.16 + 2.56 + 0.16 + 5.76
= 11.2
5. Divide the sum of squared deviations by (n-1), where n is the number of measurements:
Sample variance (s²) = Sum of squared deviations / (n-1)
= 11.2 / (5-1)
= 11.2 / 4
= 2.8
Therefore, the sample variance using the definition formula is s^2 = 2.8.
To calculate the sample variance, s², using the computing formula, you can follow these steps:
1. Find the mean (average) of the measurements (x-bar) as calculated previously:
Mean (x-bar) = 3.4
2. Calculate the squared deviation of each measurement from the mean:
Squared deviation = (measurement - mean)^2
= (5 - 3.4)², (3 - 3.4)², (5 - 3.4)², (3 - 3.4)², (1 - 3.4)²
= 1.6², -0.4², 1.6², -0.4², -2.4²
= 2.56, 0.16, 2.56, 0.16, 5.76
3. Calculate the sum of the squared deviations:
Sum of squared deviations = 2.56 + 0.16 + 2.56 + 0.16 + 5.76
= 11.2
4. Divide the sum of squared deviations by (n), where n is the number of measurements:
Sample variance (s²) = Sum of squared deviations / n
= 11.2 / 5
= 2.24
Therefore, the sample variance using the computing formula is S² = 2.24.
To calculate the sample standard deviation, s, you need to take the square root of the sample variance (s²):
s = √(s²)
= √(2.24)
≈ 1.496 (rounded to three decimal places)
Therefore, the sample standard deviation is S ≈ 1.496.
learn more about sample standard deviation: https://brainly.com/question/475676
#SPJ4
Does the following equation, y= -x2 -10x +1 have a maximum or
minimum. Explain
Answers
Answer:
Step-by-step explanation:
Your y= -x2 -10x +1 should be written as y = -x^2 -10x +1. This is a quadratic function. Because the coefficient (-1) of the x^2 term is negative, we know immediately that the graph (a parabola) opens down, and thus has a maximum.
Can someone pls help me with this?

Answers
Answer:
A
Step-by-step explanation:
The answer is a because essentially what it's asking for is the y intercept.
it gives us what the value of y = 1 so all we have to do is find the constant rate of change which is 3 and subtract that from 8
8-3=5 so your answer is A
6 grade math pls help
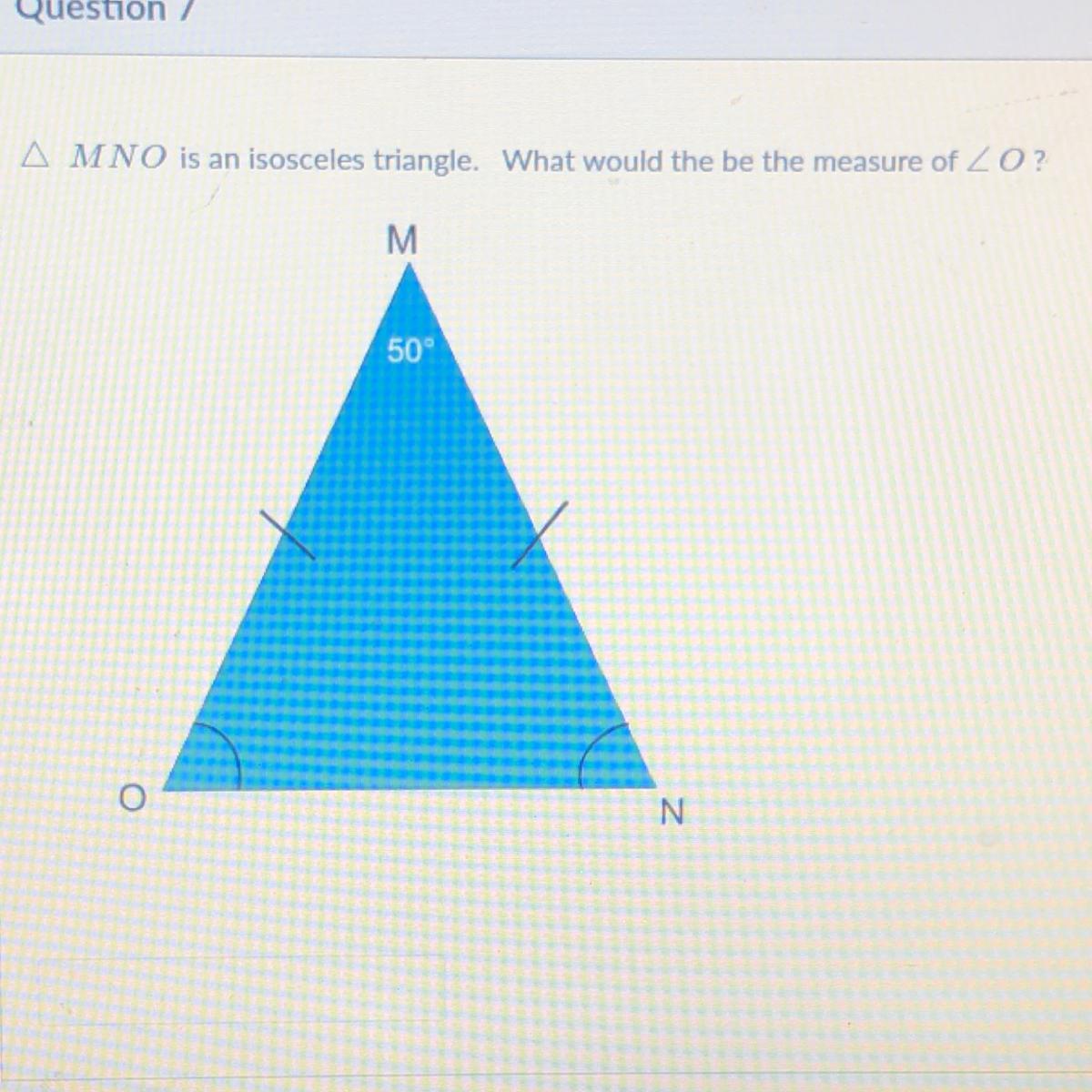
Answers
answer
measure of o is 75
and n is same as o as the sides are same
hope this helps you
If a=2, b= -1 and c=1, then find the value of:
A- a+b-c²
B- a³-b+c
C- a-b-c
Answers
Answer:
Step-by-step explanation:
A. 2 + -1 - 1^2 = 1 - 1 = 0
B. 2^3 - -1 + 1 = 8 + 1 + 1 = 10.
C. 2 - -1 - 1 = 2 + 1 - 1 = 2.
=2+(-1-1)^2
=1-1
=0
B- a³-b+c2^3-(-1+1)
=8+1+1
= 10
C- a-b-c2-(-1-1)
=2+1-1
=2
Which ones are Whole numbers?
π
-0.5
0
1123
Answers
Answer:
0 and 1123
Step-by-step explanation:
Plz mark brainlyest
also u gotta use proportions

Answers
The ratio between the time and charge is 2:3 and which defines their proportionality.
ProportionsProportion is explained majorly based on ratio and fractions. A fraction, represented in the form of a/b, while ratio a:b, then a proportion states that two ratios are equal. Here, a and b are any two integers. Proportion, in general, is referred to as a part, share, or number considered in comparative relation to a whole. Proportion definition says that when two ratios are equivalent, they are in proportion. It is an equation or statement used to depict that two ratios or fractions are equal.
In the table given, we can find the proportion between time and charge.
When time (t) = 0.5, the charge = $2.25
This can be written as 0.5 : 2.25 = 2 : 3
When time = 1, the charge = 1.5
When time = 1 1/2 = 1.5, the charge = 2.25
When time = 2, the charge = 3
Learn more on proportions here;
https://brainly.com/question/18437927
#SPJ1
Use induction to prove that for any
n∈N
, the following formula holds:
1+2+3+…+(n−1)+n= 2
n(n+1)
Answers
By induction, the formula 1+2+3+…+(n−1)+n= 2n(n+1) is true for any n∈N.
To prove the formula 1+2+3+…+(n−1)+n= 2n(n+1) by induction, we need to first establish the base case and then show that the formula holds for any n∈N by assuming it is true for n=k and then proving it is true for n=k+1.
Base case: n=1
1= 2(1)(1+1)
1= 2(2)
1= 4
This is true, so the base case holds.
Inductive step:
Assume the formula is true for n=k, that is:
1+2+3+…+(k−1)+k= 2k(k+1)
Now we need to show that the formula is true for n=k+1:
1+2+3+…+(k−1)+k+(k+1)= 2(k+1)(k+1+1)
We can use the assumption that the formula is true for n=k and substitute it into the left side of the equation:
2k(k+1)+(k+1)= 2(k+1)(k+1+1)
Distributing the 2 on the left side of the equation:
2k^2+2k+k+1= 2(k+1)(k+2)
Simplifying:
2k^2+3k+1= 2(k^2+3k+2)
Distributing the 2 on the right side of the equation:
2k^2+3k+1= 2k^2+6k+4
Subtracting 2k^2+3k+1 from both sides of the equation:
0= 3k+3
Dividing by 3:
0= k+1
This is true for any k∈N, so the formula holds for n=k+1. Therefore, by induction, the formula 1+2+3+…+(n−1)+n= 2n(n+1) is true for any n∈N.
To know more about induction refer here:
https://brainly.com/question/1463246#
#SPJ11
If you invest $10000 compounded continuously at 6% p.a. how much will this investment be worth in 6 years?
Answers
Your investment of $10000 compounded continuously at 6% p.a. would be worth $14,366.00 after 6 years.
If you invest $10000 compounded continuously at 6% p.a., the formula for calculating the value of your investment after 6 years would be:
A = Pe^(rt)
Where A is the final amount, P is the principal investment amount, e is Euler's number (approximately 2.718), r is the interest rate (in decimal form), and t is the time period (in years).
Plugging in the given values, we get:
A = 10000e^(0.06*6)
A = 10000e^(0.36)
A = 10000*1.4366
A = $14,366.00
Therefore, your investment of $10000 compounded continuously at 6% p.a. would be worth $14,366.00 after 6 years.
Learn more about compounded continuously here:
brainly.com/question/14652283
#SPJ11
The number of visible defects on a product container is thought to be Poisson distributed with a mean equal to 2.1. Based on this, how many defects should be expected if 2 containers are inspected?
Answers
We would expect to see approximately 4.2 defects in total if two containers are inspected.
If the number of visible defects on a product container follows a Poisson distribution with a mean of 2.1, then the probability of having x defects on a single container is given by:
P(X = x) = \(e^(-2.1) * (2.1)^x / x!\)
where e is the mathematical constant approximately equal to 2.71828.
To find the expected number of defects in two containers, we can use the linearity of expectation, which states that the expected value of a sum of random variables is equal to the sum of their expected values. Therefore, the expected number of defects in the two containers is:
E(X1 + X2) = E(X1) + E(X2)
Since the Poisson distribution is memoryless, the expected number of defects in one container is equal to the mean, which is 2.1. Therefore:
E(X1 + X2) = E(X1) + E(X2) = 2.1 + 2.1 = 4.2
So, we would expect to see approximately 4.2 defects in total if two containers are inspected.
Learn more about random variables
https://brainly.com/question/17238189
#SPJ4
Determine values of h and k such that the following system x1 + hx2 = 2 4x1 + 8x2 = k has (a) no solution. (b) a unique solution. In this case, what is the solution?(c) infinitely many solutions. In this case, what is the solution?
Answers
a) To determine values of h and k such that the system x1 + hx2 = 2, 4x1 + 8x2 = k has (a) no solution, set the determinant of the system equal to zero: h*8 - 4*2 = 0. Solving for h yields h = 8/2 = 4, and setting k equal to 8 yields a no solution.
b) To determine values of h and k such that the system x1 + hx2 = 2, 4x1 + 8x2 = k has (b) a unique solution, set the determinant of the system not equal to zero: h*8 - 4*2 ≠ 0. Solving for h yields h ≠ 4, and setting k equal to 8 yields a unique solution of x1 = 1 and x2 = 1.
c) To determine values of h and k such that the system x1 + hx2 = 2, 4x1 + 8x2 = k has (c) infinitely many solutions, set the determinant of the system equal to zero: h*8 - 4*2 = 0. Solving for h yields h = 4, and setting k equal to 8 yields infinitely many solutions of the form x1 = k1, x2 = k2, where k1 and k2 are any real numbers.
Learn more about Infinitely solutions
brainly.com/question/29093214
#SPJ11
Select the car that travels the fastest. choose 1 answer: choose 1 answer: (choice a, checked) a 50 50 km/h km/hcar a (choice b) b car b travels a distance of d dd kilometers in h hh hours, based on the equation 55 h = d 55h=d55, h, equals, d. (choice c) c car c travels 135 135135 kilometers in 3 33 hours. see more
Answers
The car with the speed of 50 Km/h travels the fastest.
We have given with three choices for selecting the fastest speed from them. The three choices are
First choice is 50 Km/h.
Second Choice is car b travels a distance of d kilometers in h hours, based on the equation 55 h = d , h, equals, d.. So from this be can conclude that this car is moving with the speed of (1/55)km/h.
Third choice is car c travels 135 kilometers in 3 hours. So from this be can conclude that this car is moving with the speed of (135/3) Km/h i.e., 45 Km/h.
So, from the given choices we can conclude that the car with the speed of 50 Km/h travels the fastest.
To know more about Speed refer to the link:
https://brainly.com/question/13943409
#SPJ4
Divide.
30)1777 30)1777
Answers
Answer:
434433444444444446666%$"$$$
please help if you can, vv appreciated!!

Answers
Answer:
I believe 72
Step-by-step explanation:
Solve the right triangle. Write your answers in a simplified, rationalized form. Do not round.

Answers
For the given right triangle, we can see that:
UV = 2√11
TV = √33
mU = 60°
How to find the missing measures?Here we can see a right triangle where we know one angle and the opposite cathetus, first we can find the hypotenuse using:
sin(angle) = (opposite cathetus)/hypotenuse.
Replacing the values that we know, we will get:
sin(30°) = √11/UV
Then:
UV = √11/sin(30°) = 2√11
For TV we can use the tangent function:
tan(30°) = √11/TV
TV = √11/tan(30°) = √11*√3 = √33
Finally, for the measure of U, we know that the sum of the 3 interior angles must be 180°, and one measures 90° and one 30°, then:
30 + 90 + U = 180
U = 180 - 30 - 90
U = 60
Learn more about right triangles at:
https://brainly.com/question/2217700
#SPJ1
nouOR
36, 27,
81
4'
Find the 10th term.
Submit Answer

Answers
Answer:
177
Step-by-step explanation:
Answer: a_10 = 177147/65536. Write the general term through the pattern:: a_n = 36 3/4 n - 1 Substitute and calculate:: a_10 = 177.
what is the total angle measure of a 5 sided polygon
Answers
Answer:
540 degrees (interior angles)
Step-by-step explanation:
The sum of a number and 13 is the same as the difference of 29 and the number. Find the number.
Answers
Answer:
16
Step-by-step explanation:
im pretty sure
Which of the following inequalities is graphed on the coordinate plane? A.y≤-2x=+1
Answers
Answer:
y≤-2x=+1
Step-by-step explanation:
this will definitely on coordinate plan.
Kindly completed your question as it seem unfinished
Pls help with this answer

Answers
When b is 3, the value of the expression \(2b^3 + 5\) is 59.
To evaluate the expression\(2b^3 + 5\) when b is 3, we substitute the value of b into the expression and perform the necessary calculations.
Given that b = 3, we substitute this value into the expression:
\(2(3)^3 + 5\)
First, we evaluate the exponent, which is 3 raised to the power of 3:
2(27) + 5
Next, we perform the multiplication:
54 + 5
Finally, we add the two terms:
59
Therefore, when b is 3, the value of the expression \(2b^3 + 5\) is 59.
In summary, by substituting b = 3 into the expression \(2b^3 + 5\), we find that the value of the expression is 59.
It's important to note that the provided equation has multiple possible solutions for x, but when b is specifically given as 3, the value of x is approximately 3.78.
It's important to note that in this equation, we substituted the value of b and solved for x, resulting in a specific value for x. However, if we wanted to solve for b given a specific value of x, we would follow the same steps but rearrange the equation accordingly.
For more such question on expression visit:
https://brainly.com/question/1859113
#SPJ8
The expression 3x-y is a term. True or false
Answers
Answer:
False
Step-by-step explanation:
It has two parts that is separated by a minus.
a set of 10 coins may contain any combination of pennies, nickles, dimes, quarters, or half-dollars. in how many different ways can the set of 10 coins have a total value of 59c?
Answers
There are 46 different ways in which a set of 10 coins can have a total value of 59 cents.
To find the number of different ways, we can use a systematic approach. Let's consider the five types of coins: pennies (1 cent), nickels (5 cents), dimes (10 cents), quarters (25 cents), and half-dollars (50 cents).
Since we need a total value of 59 cents, we can start by using as many half-dollars as possible. The maximum number of half-dollars that can be used is one since two half-dollars would already exceed the required total.
Next, we can iterate through the remaining values and combinations of the remaining coins (quarters, dimes, nickels, and pennies) to find all possible ways to reach 59 cents. We can use nested loops to generate all the combinations. By trying different combinations, we find that there are 46 different ways to achieve a total value of 59 cents using 10 coins.
There are 46 different ways in which a set of 10 coins can have a total value of 59 cents. This calculation takes into account all possible combinations of pennies, nickels, dimes, quarters, and half-dollars.
To know more about combinations, visit;
https://brainly.com/question/20211959
#SPJ11
HELP ME PLZZZZZZZZZZ
What are the next three numbers in this sequence: 7, 16, 25, 34...?
0 45, 56, 65
43, 54, 65
42, 40, 58
43, 52, 61

Answers
Answer:
43, 52, 61
(adding nine each time)
There are 3 right triangles in the drawing below. They are all similar. Chose the correct
similarity statement.
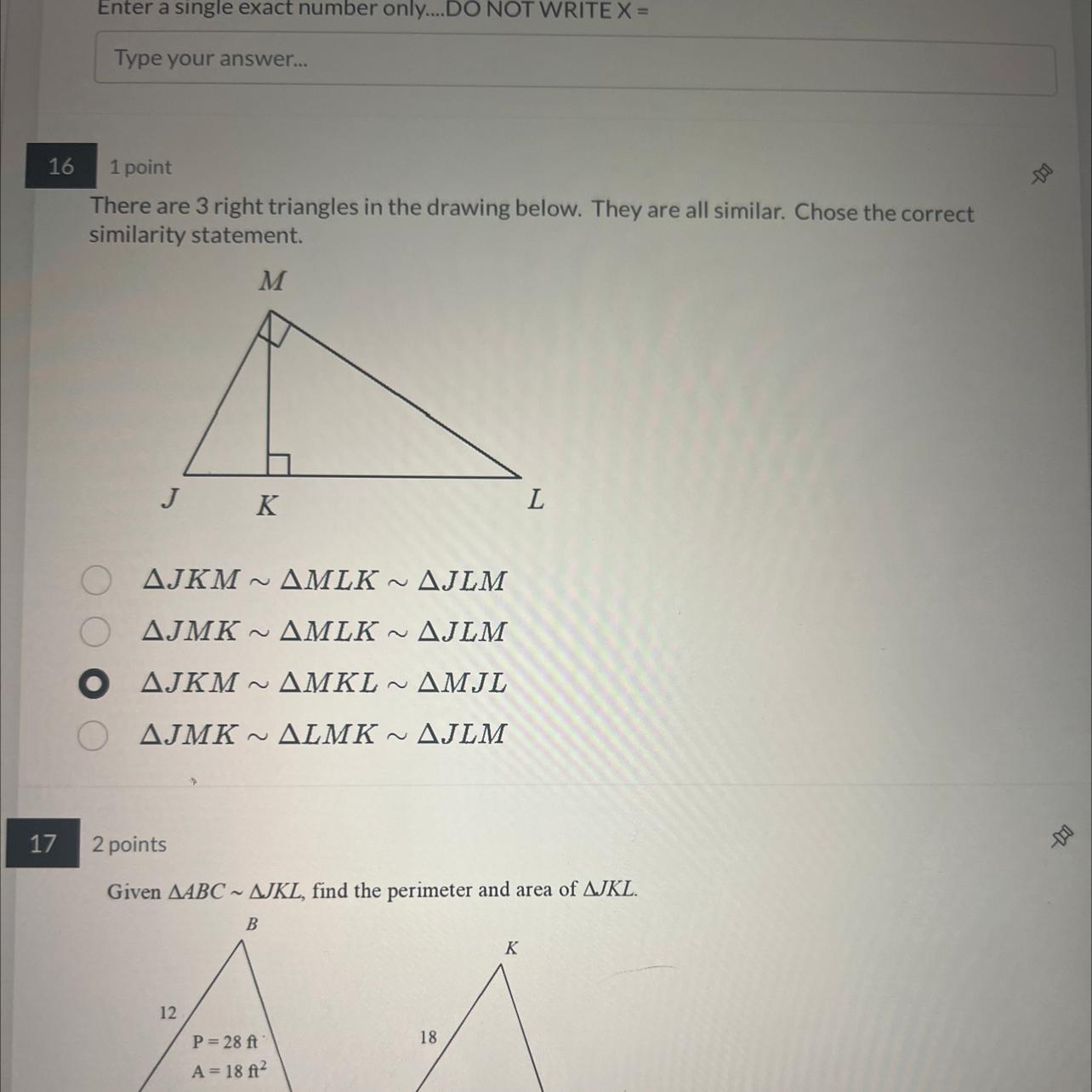
Answers
The correct similarity of the triangles are JMK ~ LMK ~ JLM (option D)
What is similarity?Two figures are considered to be "similar figures" if they have the same shape, congruent corresponding angles and equal scale factors. Equal scale factors mean that the lengths of their corresponding sides have a matching ratio.
Given that, there are 3 right triangles in the drawing given. They are all similar. we need to identify the correct similarity,
So, from the figure, if we separate each triangle,
We will get,
Triangles JLM, JMK and LMK
If we check,
They are showing true similarity by their figure (refer to diagram attached)
Hence, the correct similarity of the triangles are JMK ~ LMK ~ JLM (correct option is D)
Learn more about similarity, click;
https://brainly.com/question/26451866
#SPJ1

In △JKL, LO=104 cm.
What is the length of NO¯¯¯¯¯¯?
Enter your answer in the box.

Answers
Answer:
The answer is 52 cm
Step-by-step explanation:
Answer: 52 cm
Step-by-step explanation:

can you please help me with this one

Answers
Answer:
6x=-60
Step-by-step explanation:
if p = 2^k + 1 is prime, show that every quadratic nonresidue of p is a primitive root of p.
Answers
Every quadratic nonresidue of p is a primitive root of p, when p = 2^k + 1 is primeIf p = 2^k + 1 is a prime number, we want to show that every quadratic nonresidue of p is a primitive root of p.
In other words, we aim to prove that if an element x is a quadratic nonresidue modulo p, then it is also a primitive root of p.
Let's assume p = 2^k + 1 is a prime number. To prove that every quadratic nonresidue of p is a primitive root of p, we can use the properties of quadratic residues and quadratic nonresidues.
A quadratic residue modulo p is an element y such that y^((p-1)/2) ≡ 1 (mod p), while a quadratic nonresidue is an element x such that x^((p-1)/2) ≡ -1 (mod p).
Now, let's consider an element x that is a quadratic nonresidue modulo p. We want to show that x is a primitive root of p.
Since x is a quadratic nonresidue, we know that x^((p-1)/2) ≡ -1 (mod p). By Euler's criterion, this implies that x^((p-1)/2) ≡ -1^((p-1)/2) ≡ -1^2 ≡ 1 (mod p).
Since x^((p-1)/2) ≡ 1 (mod p), we can conclude that the order of x modulo p is at least (p-1)/2. However, since p = 2^k + 1 is a prime, the order of x modulo p must be equal to (p-1)/2.
By definition, a primitive root of p has an order of (p-1). Since the order of x modulo p is (p-1)/2, it follows that x is a primitive root of p.
Learn more about Euler's criterion here:
brainly.com/question/12977984
#SPJ11