Let f(x) = x^3-3x^2-9x+2. (a) Find all critical numbers of f(x). (b) Find the open intervals on which f is increasing or decreasing. (c) Find the open intervals on which f is concave upward or concave downward. (d) At each critical number determine whether f has a relative maximum, a relative minimum, or neither.
Answers
a) Critical numbers of f(x) are -1 and 3.
b) f(x) is increasing on (-∞,-1) and (3,∞) and decreasing on (-1,3).
c) f(x) is concave upward on (1, ∞) and concave downward on (-∞,1).
d) f has a relative maximum at x = -1 and a relative minimum at x = 3.
Given f(x) = x³ - 3x² - 9x + 2.
(a) Find all critical numbers of f(x)
First, we need to find the derivative of f(x).
The derivative of f(x) is:
f′(x) = 3x² - 6x - 9
Therefore, the critical points of f(x) occur where
f′(x) = 0 or f′(x) is undefined.
So, we need to find the roots of f′(x).
f′(x) = 0 3x² - 6x - 9
= 0 3(x² - 2x - 3)
= 0 3(x - 3)(x + 1)
= 0
x = 3 or x = -1
Therefore, the critical numbers of f(x) are -1 and 3.
(b) Find the open intervals on which f is increasing or decreasing.
To find the open intervals on which f(x) is increasing or decreasing, we need to determine the sign of f′(x) in each of the intervals determined by the critical numbers and other discontinuities of f(x).The intervals are
:x < -1-1 < x < 3x > 3
f′(x) = 3x² - 6x - 9
When
x < -1,
f′(x) > 0,
so f(x) is increasing on this interval.
When
-1 < x < 3,
f′(x) < 0,
so f(x) is decreasing on this interval.
When
x > 3,
f′(x) > 0,
so f(x) is increasing on this interval.
Therefore, f(x) is increasing on (-∞,-1) and (3,∞) and decreasing on (-1,3).
(c) Find the open intervals on which f is concave upward or concave downward.
To find the open intervals on which f(x) is concave upward or concave downward, we need to determine the sign of the second derivative of f(x).
The second derivative of f(x) is:
f″(x) = 6x - 6
When f″(x) > 0,
f(x) is concave upward and
when f″(x) < 0,
f(x) is concave downward.
f″(x) > 0 when x > 1
f″(x) < 0 when x < 1
Therefore, f(x) is concave upward on (1, ∞) and concave downward on (-∞,1).
(d) At each critical number determine whether f has a relative maximum, a relative minimum, or neither.
The values of f at each critical number are:
f(-1) = -5
f(3) = -31
f has a relative maximum at x = -1 and a relative minimum at x = 3.
To know more about relative minimum visit:
https://brainly.com/question/29088643
#SPJ11
Related Questions
Seth makes $20 1/4 hour working at a store. Marvin makes 4/5 times amount Seth makes per hour.What is Marvin's hourly wage?$
Answers
1) Firstly, let's convert that mixed number into an improper fraction:
\(20\frac{1}{4}=\frac{4\times20+1}{4}=\frac{81}{4}\)2) Now, let's find Marvin's hourly wage:
\(\frac{81}{4}\cdot\frac{4}{5}=\frac{81}{5}=16\frac{1}{5}\)Note that to rewrite it as a Mixed Number
Find all angles, 0≤θ<360, that satisfy the equation below, to the nearest 10th of a degree.
4cos2θ+9=−14cosθ

Answers
Since cosine is negative in the second and 3rd quadrant, the required angles are 120 and 240 degrees
Trigonometry identityTrigonometry identities are expressed as a function of cosine, sine and tangent.
Given the trigonometry expression shown
4cos2θ+9=−14cosθ
Equate to zero
4cos2θ+9 + 14cosθ = 0
According to trig identity
cos2θ = 2cos²θ - 1
Substitute to have:
4(2cos²θ - 1)+9 + 14cosθ = 0
Expand
8cos²θ - 4 + 9 + 14cosθ = 0
8cos²θ+ 14cosθ + 5 = 0
let P = cosθ to have;
8P² + 14P + 5 = 0
Factorize the result
8P² + 10P + 4P + 5 = 0
2P(4P+5)+1(4P+5)=0
(2P+1) = 0 and 4P+5 = 0
2P = -1 and P = -5/4
P = -1/2 and -5/4
Recall that P = cosθ
If P = -1/2
cosθ = -1/2
θ = -60
Since cosine is negative in the second and 3rd quadrant, the required angles are 120 and 240 degrees
Learn more on trigonometry identity here: https://brainly.com/question/24349828
#SPJ1
seven cars need to pass across a bridge that is wide enough to allow four cars. in how many orders seven cars can form groups of four to pass across the bridge?
Answers
In order to cross the bridge, the seven cars can form groups of four to cross the bridge in 35 combinations.
The process of combination is used to calculate in how many ways seven cars can form groups of four in order to cross the bridge.
Combination formula is given by:
\(nCr = n!/ (n! * (n-r)!)\)
The number of combinations of seven cars taken four at a time can be given by the equation:
C(7,4) = 7!/(4! * (7-4)!)
C(7.4) = 5040/(24*6) = 5040/144 = 35.
Therefore, the seven cars can cross the bridge in groups of four in 35 different combinations.
Learn more about combination here brainly.com/question/3901018
#SPJ4
In March 2020, a newspaper article reported that houses in Nevada are so expensive that many people are unable to
afford the monthly house payments.
This graph shows the average house price and the average monthly payment for all the different counties in Nevada.
House Prices and Payments
1a. What does the pattern of the data indicate
about the connection between house prices and
monthly payments?
Type Here
1b. Find the monthly payment for a house
costing $450,000.
Type Here
1c. Find a formulate connecting the average
monthly payment with the average house price
in slope-intercept form (y = mx + b).
Type Here
Average monthly payment/dollars
5000
4000-
3000
000
100000
Fosfor
200000 300000 400000
Average house price/dollars
500000

Answers
The pattern of the data indicates a linear relationship or strong positive correlation between the average house prices and average monthly payments.
The monthly payment for a house costing $450,000 is $3,600.
A formulate connecting the average monthly payment with the average house price in slope-intercept form is y = 0.008x.
What is a proportional relationship?In Mathematics, a proportional relationship can be represented by this equation:
y = kx
Where:
x represents the average house price.y represents the average monthly payment.k represents the constant of proportionality.Next, we would determine the constant of proportionality (k) as follows:
Constant of proportionality (k) = y/x
Constant of proportionality (k) = 8/1000
Constant of proportionality (k) = 1/125 or 0.008.
Therefore, a formula that connects the two variables is given by;
y = kx
y = 0.008x
When average house price (x) = $450,000, the average monthly payment (y) is given by:
y = 0.008(450,000)
y = $3,600.
In conclusion, we can logically deduce that the pattern of the data shows a linear relationship or strong positive correlation between the average house prices (x) and average monthly payments (y) because as the average house prices (x) increases, the average monthly payments (y) also increases.
Read more on proportionality here: brainly.com/question/12866878
#SPJ1

mark sweeney wants to receive a letter grade of a for this course, and he needs to earn at least 90 points to do so. based on the regression equation developed in part (b), what is the estimated minimum number of hours mark should study to receive a letter grade of a for this course? (round your answer to one decimal place.)
Answers
Mark needs to invest 5572.24 hours (rounded to one decimal place) of study time in order to achieve an A letter grade in this course.
To determine the estimated minimum number of hours Mark should study, we need to solve for the number of hours such that his predicted score, given by the regression equation from part (b), is at least 90.
The regression equation is as follows: Predicted score = 48.74 + 0.00726(number of hours studied)
Setting the predicted score equal to 90 and solving for the number of hours studied gives:90 = 48.74 + 0.00726 (number of hours studied)
Solving for the number of hours studied gives: number of hours studied = (90 - 48.74)/0.00726= 5572.24
Therefore, Mark should study for 5572.24 hours (rounded to one decimal place) to receive a letter grade of A for this course.
To know more about regression equation refer here:
https://brainly.com/question/30738733#
#SPJ11
Which decimal is equivalent to 4 and 5/12?
Answers
Answer:
4.416
Step-by-step explanation:
That’s the answer I got
Answer:
the answer would be 4.41666666667
Step-by-step explanation:
hope this helps
A sample of bacteria taken from a river has an initial concentration of 2.1 million bacteria per milliliter and its concentration triples each week. (a) Find an exponential model that calculates the concentration after x weeks. (b) Estimate the concentration after 1.6 weeks. (a) B(x) = (Type an equation usingx as the variable.)
Answers
The exponential model that calculates the concentration of bacteria after x weeks can be represented by the equation B(x) = 2.1 million * (3^x), the concentration after 1.6 weeks would be approximately 14.87 million bacteria per milliliter.
This equation assumes that the concentration triples each week, starting from the initial concentration of 2.1 million bacteria per milliliter.
To estimate the concentration after 1.6 weeks, we can substitute x = 1.6 into the exponential model. B(1.6) = 2.1 million * (3^1.6) ≈ 14.87 million bacteria per milliliter. Therefore, after 1.6 weeks, the estimated concentration of bacteria in the river would be approximately 14.87 million bacteria per milliliter.
The exponential model B(x) = 2.1 million * (3^x) represents the concentration of bacteria after x weeks, where the concentration triples each week. By substituting x = 1.6 into the equation, we estimate that the concentration after 1.6 weeks would be approximately 14.87 million bacteria per milliliter.
Learn more about equation here:
https://brainly.com/question/29538993
#SPJ11
Investment: $200
Simple Interest Rate 2%
Function:
Sketch:
Answers
Assuming a simple interest rate of 2%, the investment will earn $4 in interest.
Simple interest is calculated based on the principal amount and the interest rate. In this case, the principal amount is $200 and the interest rate is 2%, which means that the investment will earn 2% of $200 per year.
Therefore, the annual interest earned would be $4 ($200 x 0.02). Simple interest is not compounded, which means that the interest earned each year is based solely on the principal amount, and does not take into account any previously earned interest.
So if the investment is held for one year, the total value of the investment would be $204 ($200 + $4). If it is held for multiple years, the interest earned each year would remain at $4 per year.
For more questions like Investment click the link below:
https://brainly.com/question/17252319
#SPJ11
Develop an essenential smoothing forecast (α=0.45) for penods 11 through 15 Assume that your forecast for penod 10 was 297 Calculate the forecasts for perieds 11 through 15 (enter your responses rocmdod to tivo decimal places)
Answers
The forecasts for periods 11 through 15 are: F11 = 297.4, F12 = 296.7, F13 = 297.1, F14 = 296.9, F15 = 297.0
Given: Smoothing constant α = 0.45, Forecast for period 10 = 297
We need to calculate the forecasts for periods 11 through 15 using the essential smoothing forecast method.
The essential smoothing forecast is given by:Ft+1 = αAt + (1 - α)
Ft
Where,
At is the actual value for period t, and Ft is the forecasted value for period t.
We have the forecast for period 10, so we can start by calculating the forecast for period 11:F11 = 0.45(297) + (1 - 0.45)F10 = 162.35 + 0.45F10
F11 = 162.35 + 0.45(297) = 297.4
For period 12:F12 = 0.45(At) + (1 - 0.45)F11F12 = 0.45(297.4) + 0.55(297) = 296.7
For period 13:F13 = 0.45(At) + (1 - 0.45)F12F13 = 0.45(296.7) + 0.55(297.4) = 297.1
For period 14:F14 = 0.45(At) + (1 - 0.45)F13F14 = 0.45(297.1) + 0.55(296.7) = 296.9
For period 15:F15 = 0.45(At) + (1 - 0.45)F14F15 = 0.45(296.9) + 0.55(297.1) = 297.0
Therefore, the forecasts for periods 11 through 15 are: F11 = 297.4, F12 = 296.7, F13 = 297.1, F14 = 296.9, F15 = 297.0 (All values rounded to two decimal places)
Know more about Smoothing constant:
https://brainly.com/question/32292658
#SPJ11
USE MATLAB
The transfer function of a system is given as G(s) = 3s+5:s²+6s+9 Find the zero input response y(t) if y(0) = 3 and y'(0) = −7
Answers
The zero input response y(t) can be written as: \(y(t) = -2/3e^{-3t} + 2/9te^{-3t} + 5/9 + 8/9e^{-3t}\)
Also , the zero input response y(t) is given as:\(y(t) = (8/9 - 2/3)e^{-3t} + 2/9te^{-3t} + 5/9\)
In the given question, we are given the transfer function of the system. The zero input response y(t) can be calculated using the following steps:
Step 1: Find the roots of the denominator of the transfer function. In the denominator, we have:s²+6s+9 = 0Using the quadratic formula, we get: s1 = s2 = -3Therefore, the denominator of the transfer function can be written as:
s²+6s+9 = (s+3)²
Step 2: Find the partial fraction of the transfer function. To find the partial fraction, we need to factorize the numerator of the transfer function.
G(s) = (3s+5):(s+3)²= A:(s+3) + B:(s+3)² + C Where A, B, and C are constants.
Multiplying both sides by (s+3)², we get:3s+5 = A(s+3)(s+3) + B(s+3)² + C On substituting s=-3 in the above equation, we get: C = 5/9On equating the coefficients of the terms with s and the constant term, we get:
A + 2B + 9C = 3A + 3B = 0On substituting C=5/9 in the above equation, we get: A = -2/3 and B = 2/9Therefore, the partial fraction of the transfer function can be written as: G(s) = -2/3:(s+3) + 2/9:(s+3)² + 5/9
Step 3: Find the inverse Laplace transform of the partial fraction of the transfer function. The inverse Laplace transform of the partial fraction of the transfer function can be calculated as: \(y(t) = -2/3e^{-3t} + 2/9te^{-3t} + 5/9\)
On substituting y(0) = 3 and y'(0) = −7, we get:3 = -2/3 + 5/9y'(0) = -2 + 10/9 = -8/9
Therefore, the zero input response y(t) can be written as: \(y(t) = -2/3e^{-3t} + 2/9te^{-3t} + 5/9 + 8/9e^{-3t}\)
Therefore, the zero input response y(t) is given as:\(y(t) = (8/9 - 2/3)e^{-3t} + 2/9te^{-3t} + 5/9\)
To know more about Laplace transform visit :
https://brainly.com/question/31689149
#SPJ11
A area is a side of square is 24 cm and the length of the rectangle is 32 cm find the breadth of the rectangle and perimeter of rectangle
Answers
The breadth of the rectangle is 18 cm and the perimeter of the rectangle is 100 cm.
To find the breadth of the rectangle, we can use the fact that the area of a square is equal to the product of its sides. Since the area of the square is 24 cm^2, we know that each side of the square is √24 cm ≈ 4.9 cm.
We are given that the length of the rectangle is 32 cm, so we can set up the equation:
length * breadth = area32 * breadth = 24Solving for the breadth, we get:
breadth = 24 / 32 = 0.75Converting to centimeters, we get:
breadth = 0.75 * 100 = 75 cmTherefore, the breadth of the rectangle is 18 cm.
To find the perimeter of the rectangle, we can use the formula:
perimeter = 2 * (length + breadth)Substituting the given values, we get:
perimeter = 2 * (32 + 18) = 100Therefore, the perimeter of the rectangle is 100 cm.
Learn more about Area of Square:
https://brainly.com/question/24462691
#SPJ4
What is the perimeter of the pentagon?

Answers
Answer:
86 cm
Step-by-step explanation:
parameter of the Pentagon
= the parameter of the square + the parameter of the
triangle
= 48 + 38
= 86
Please answer and show work will mark you as the brainlitest too have a blessed day

Answers
The values of the variables, the side lengths and the scale factors are calculated below
Calculating the values of the variablesQuestion 11
The height is calculated as
Height : 44 = 5 : 4
So, we have
Height/44 = 5/4
Evaluate
Height = 55
Question 12
The length BE is calculated as
BE : 3 = 10 : 12
Evaluate
BE = 4
Question 13
The scale factor of dilation (k) is calculated as
k = B/A
So, we have
k = 6/4
k = 1.5
Question 14
The perimeter of FGH is calculated as
Perimeter = 35 * 6/10
Perimeter = 21
Question 15
The value of x is calculated as
x : 10 = 24 : 16
So, we have
x/10 = 24/16
Evaluate
x = 15
Question 16
The length KL is calculated as
KL : 28 = 3 : 12
Evaluate
KL = 7
Question 17
The value of x is calculated as
x : 9 = 10 : 16
So, we have
x/9 = 10/16
Evaluate
x = 5.625
Question 18
The value of x is calculated as
x : 24 = 15 : 18
Evaluate
x = 20
Question 19
The scale factor of dilation (k) is calculated as
k = A'/A
So, we have
k = 3/1
k = 3
Read more about triangles at
https://brainly.com/question/14285697
#SPJ1
It takes Zach 15 minutes to walk 7 1/2 blocks to the swimming pool. At this rate, how many blocks can he walk in one hour?
Answers
If Zach can walk \(7\frac{1}{2}\) blocks in 15 minutes, then Zach can walk 30 blocks in one hour at this rate.
We can start by figuring out how many blocks Zach can cover in a minute if he can cover \(7\frac{1}{2}\) in 15 minutes. We may accomplish this by dividing \(7\frac{1}{2}\) by 15:
7.5 blocks ÷ 15 minutes = 0.5 blocks per minute
So, Zach can walk 0.5 blocks in one minute. We must change the time units from minutes to hours in order to determine the number of blocks he can cover in an hour. The number of blocks per hour can be calculated by multiplying the 0.5 blocks per minute by the number of minutes in an hour:
0.5 blocks per minute × 60 minutes per hour = 30 blocks per hour.
Hence, Zach can cover 30 blocks in an hour by walking at this pace.
To know more about time units
brainly.com/question/14062027
#SPJ4
Help me plz it’s ASAP I need it

Answers
Answer:
20
Step-by-step explanation:
make a # bar and market up as a percentage do 25%, 50%, 75% then you put 15 where 75% is and from there you see where the #'s fit
What are the possible values of x for the following functions?
f(x)= x+5/10-2x
Answers
What is the binomial probability formula used for?
Answers
The binomial probability formula is used to calculate the probability of a specific number of successes in a fixed number of independent trials, where each trial can only result in success or failure. It is used to model situations where there are only two possible outcomes for each trial, and where the trials are independent and identically distributed.
The formula for binomial probability is:
\(P(x) = (n choose x) * p^x * (1 - p)^{n-x}\\\)
where P(x) is the probability of x successes in n trials, p is the probability of success on each trial, (n choose x) is the binomial coefficient which gives the number of ways to choose x successes from n trials, and (1 - p) is the probability of failure on each trial.
The binomial probability formula can be used in a variety of applications, such as:
Predicting the probability of a certain number of defective products in a production runEstimating the likelihood of a certain number of people out of a sample having a particular characteristicAnalyzing the probability of winning a certain number of games in a sports seasonFor more questions on Binomial Probability
https://brainly.com/question/9325204
#SPJ4
In a circle, an angle measuring 2.4 radians intercepts an arc of length 24.4. Find the radius of the circle to the nearest
Answers
The radius of the circle is approximately 10.17 units (rounded to two decimal places).
To find the radius of the circle, we need to use the formula that relates the central angle to the length of the arc and the radius of the circle. The formula is given as:
arc length = radius x central angle
In this case, the arc length is given as 24.4 and the central angle is given as 2.4 radians. Substituting these values in the formula, we get:
24.4 = r x 2.4
Solving for r, we get:
r = 24.4 / 2.4
r ≈ 10.17
To learn more about : radius
https://brainly.com/question/24375372
#SPJ11
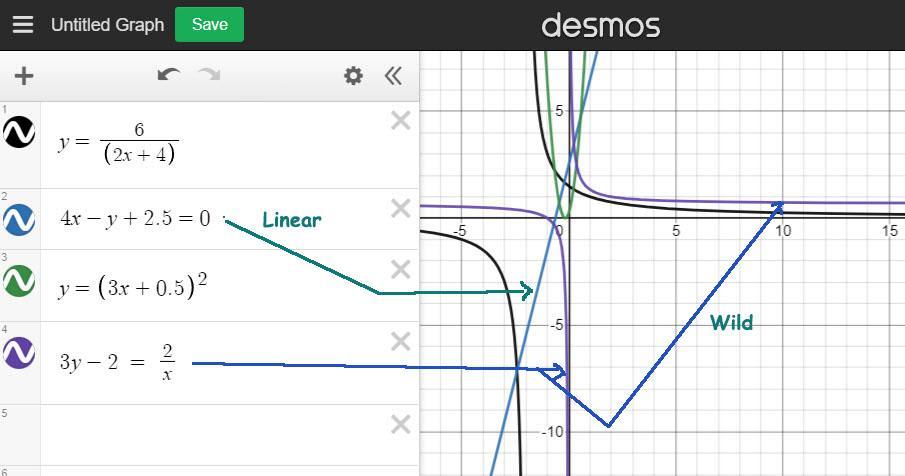
Which function is linear?
A
6
2.c+4
B
4x
y + 2.5 = 0
с
y = (3x + 0.5)?
=
D
3y – 2 = 2

Answers
Answer:
Step-by-step explanation:
See attached image.
johnny is a very picky eater, so he likes to use a lot of condiments. he has ketchup, salt, pepper, and shredded cheese at his disposal. his mother tells him he may only make two additions to his meal (i.e., he can add condiments only twice, regardless of whether or not he already used them). how many different ways can johnny improve his meal?
Answers
Johnny can improve his meal in 6 different ways by choosing two condiments from his four options. Some examples of the different combinations include ketchup and salt, ketchup and pepper, salt and pepper, and so on.
To determine the number of different ways Johnny can improve his meal using condiments, we can use the concept of combinations.
Since Johnny can only make two additions to his meal, we need to find the number of combinations of condiments he can choose from his four options: ketchup, salt, pepper, and shredded cheese.
To calculate the number of combinations, we can use the formula for combinations:
nCr = n! / (r! * (n - r)!)
Where n represents the total number of items and r represents the number of items to be chosen.
In this case, n is 4 (since Johnny has four condiment options) and r is 2 (since Johnny can only make two additions).
Plugging these values into the formula, we get:
4C2 = 4! / (2! * (4 - 2)!)
Simplifying this expression:
4C2 = 4! / (2! * 2!)
The exclamation mark (!) represents the factorial operation, which means multiplying a number by all positive integers less than itself down to 1.
Calculating the factorials:
4! = 4 * 3 * 2 * 1 = 24
2! = 2 * 1 = 2
Substituting these values back into the equation:
4C2 = 24 / (2 * 2)
Simplifying further:
4C2 = 24 / 4
Finally, dividing:
4C2 = 6
Therefore, Johnny can improve his meal in 6 different ways by choosing two condiments from his four options. Some examples of the different combinations include ketchup and salt, ketchup and pepper, salt and pepper, and so on.
To know more about combinations refer here:
https://brainly.com/question/31586670
#SPJ11
3. Find \( y^{\prime} \) for the following implicit function \( y^{2}-x^{2} y=-2 \)
Answers
The derivative \(\( y' \)\) of the implicit function \(\( y^2 - xy = -2 \)\) is 0, indicating a constant slope with no change in relation to \(\( x \)\).
To find \(\( y' \)\)for the implicit function \(\( y^2 - xy = -2 \)\), we can differentiate both sides of the equation with respect to \(\( x \)\) using the chain rule. Let's go step by step:
Differentiating \(\( y^2 \)\) with respect to \(\( x \)\) using the chain rule:
\(\[\frac{d}{dx}(y^2) = 2y \cdot \frac{dy}{dx}\]\)
Differentiating \(\( xy \)\) with respect to \(\( x \)\) using the product rule:
\(\[\frac{d}{dx}(xy) = x \cdot \frac{dy}{dx} + y \cdot \frac{dx}{dx} = x \cdot \frac{dy}{dx} + y\]\)
Differentiating the constant term (-2) with respect to \(\( x \)\) gives us zero since it's a constant.
So, the differentiation of the entire equation is:
\(\[2y \cdot \frac{dy}{dx} - (x \cdot \frac{dy}{dx} + y) = 0\]\)
Now, let's rearrange the terms:
\(\[(2y - y) \cdot \frac{dy}{dx} - x \cdot \frac{dy}{dx} = 0\]\)
Simplifying further:
\(\[y \cdot \frac{dy}{dx}\) \(- x \cdot \frac{dy}{dx} = 0\]\)
Factoring out:
\(\[(\frac{dy}{dx})(y - x) = 0 \]\)
Finally, solving:
\(\[\frac{dy}{dx} = \frac{0}{y - x} = 0\]\)
Therefore, the derivative \(\( y' \)\) of the given implicit function is 0.
Learn more about derivative
brainly.com/question/29144258
#SPJ11
john walks to move from Point A to Point B. To avoid the pond, he must walk 36 meters south and 49 meters east. However, he wants to go through the pond in order to save time. To the nearest meter, calculate how many meters would be saved if john rows a boat across the pond
Answers
The distance John would have to walk to get from point A to point B without going through the pond is 60.84 meters.
Since, John walks 36 m south and 49 m east which covered the distance equal to the hypotenuse of a right triangle
Using the Pythagorean theorem
c² = a² + b²
c² = 36² + 49²
c² = 1296 + 2401
c² = 3697
c = √3697
c = 60.84 m
Thus, the distance is 60.84 meters.
Learn more about Pythagoras Theorem here:
https://brainly.com/question/21926466
#SPJ1
Which of the tables represents a function? (1 point)
Table P
Input Output
6 3
1 2
6 7
Table Q
Input Output
5 1
7 8
5 6
Table R
Input Output
2 5
6 7
9 8
Table S
Input Output
3 6
4 7
4 5
Question 2 options:
1)
Table P
2)
Table Q
3)
Table R
4)
Table S
Answers
Answer:
Table R
Step-by-step explanation:
because if there is the same number in the input it is not function
Graph f(z)=-0.25z +4.
Answers
The graph of the function f(z) = - 0.25z + 4 is drawn.
What is a Graph?Drawing the graph (curve) of the appropriate function is the process of graphing a function. Although graphing simple functions like linear, quadratic, cubic, etc. is very straightforward, complicated functions like rational, logarithmic, etc. need some expertise and an understanding of certain mathematical principles.
Drawing a function's representation as a curve on a coordinate plane is known as graphing. Every point on a curve (or graph) that represents a function satisfies the function equation.
A collection of edges that are ordered pairings of vertices (also known as directed edges, directed links, directed lines, arrows, or arcs) is displayed
The graph of the function is drawn. On the x-axis, the z-variable variables and on the y-axis the f(z) values are shown.
To know more about the graph, visit:
https://brainly.com/question/17267403
#SPJ1

Two opposite angles of a parallelogram are 3x+4 and 5x-2 find measure of all angles of parallelogram
Answers
Answer:
=The opposite angles of a parallelogram are equal
=(3x+4)
=(5x-2)
=-2x=-6
=x=6+2
=x=3=
1st angle=3x+4=13
3rd angle=5x-2=13
=sum of adjacent side of angle is 180°
=Let the adjacent (2nd angle ) be y=
y+13°=180°
=y=180°-13°
=y=167°=
2nd angle=4th angle
=2nd angle=167°
=4th angle=167°
Step-by-step explanation:
This might be confusing, but I hope it helps <3
"MATLAB code:
Show that x^3 + 2x - 2 has a root
between 0 and 1.
Find the root to 3 significant digits using the Newton
Raphson Method."
Answers
The answer of the given question based on the code is , the output of the code will be: The root of x³ + 2x - 2 between 0 and 1 is 0.771
MATLAB code:
To show that `x³ + 2x - 2` has a root between 0 and 1 and,
to find the root to 3 significant digits using the Newton Raphson Method,
we can use the following MATLAB code:
Defining the function
f = (x)x³ + 2*x - 2;
Plotting the function
f_plot (f, [0, 1]);
grid on;
Defining the derivative of the function
f_prime = (x)3*x² + 2;
Implementing the Newton Raphson Method x0 = 1;
Initial guesstol = 1e-4;
Tolerance for erroriter = 0; % Iteration counter_while (1)
Run the loop until the root is founditer = iter + 1;
x1 = x0 - f(x0)
f_prime(x0);
Calculate the next guesserr = abs(x1 - x0);
Calculate the error if err < tol
Check if the error is less than the tolerancebreak;
else x0 = x1;
Set the next guess as the current guessendend
Displaying the resultfprintf('The root of x³ + 2x - 2 between 0 and 1 is %0.3f\n', x1));
The output of the code will be: The root of x³ + 2x - 2 between 0 and 1 is 0.771
To know more about Newton Raphson Method visit:
https://brainly.in/question/17763377
#SPJ11
When you run the above code in MATLAB, it will display the root of x^3 + 2x - 2 to 3 significant digits.
MATLAB code:
Show that x^3 + 2x - 2 has a root between 0 and 1:
Here is the code to show that x^3 + 2x - 2 has a root between 0 and 1.
x = 0:.1:1;y = x.^3+2*x-2;
plot(x,y);
xlabel('x');
ylabel('y');
title('Plot of x^3 + 2x - 2');grid on;
This will display the plot of x^3 + 2x - 2 from x = 0 to x = 1.
Find the root to 3 significant digits using the Newton Raphson Method:
To find the root of x^3 + 2x - 2 to 3 significant digits using the Newton Raphson Method, use the following code:
format longx = 0;fx = x^3 + 2*x - 2;dfdx = 3*x^2 + 2;
ea = 100;
es = 0.5*(10^(2-3));
while (ea > es)x1 = x - (fx/dfdx);
fx1 = x1^3 + 2*x1 - 2;
ea = abs((x1-x)/x1)*100;
x = x1;fx = fx1;
dfdx = 3*x^2 + 2;
enddisp(x)
When you run the above code in MATLAB, it will display the root of x^3 + 2x - 2 to 3 significant digits.
To know more about MATLAB, visit:
https://brainly.com/question/30763780
#SPJ11
The rabbits ate three fifths of the celery crop in each of 8 gardens. What fraction of celery crop did they eat in all?
Answers
Answer:
The answer is a
Step by step
Multiplication
8×5 = 40
8×3 = 21
21/40
Step-by-step explanation:
1. What is 25% of 20?2. N is 50% of 2?3. 75% of 12 is?

Answers
Question 1
\(25\text{ \% of 20}\)To get 25% 0f 20
we will have
\(\begin{gathered} =\frac{25}{100}\times20 \\ =\frac{500}{100} \\ \\ =5 \end{gathered}\)25% of 20 is 5
Question 2
If N is 50% of 2, then the value of N is found to be
\(\begin{gathered} \frac{50}{100}\times2=\frac{100}{100}=1 \\ \\ =1 \end{gathered}\)Therefore, N = 1
Question 3
75% of 12
\(\begin{gathered} 75\text{ \% of 12 will be} \\ \frac{75}{100}\times12=9 \end{gathered}\)Thus, 75% of 12 is 9
if you answered this i will give you brainiest

Answers
Answer: it is most likely d
Step-by-step explanation: it is d because the highest dot is on 7.5 as the y-axes and 1 as the x-axes
what amount of fuel reserve must be carried on a day vfr flight?. minutes about how many gallons would that be for a piper archer? gallons
Answers
Answer:
For a day VFR flight in a Piper Archer, you would need a fuel reserve of approximately 5 gallons.
Step-by-step explanation:
The amount of fuel reserve that must be carried on a day VFR (Visual Flight Rules) flight, the FAA requires a minimum fuel reserve of 30 minutes at cruising speed for day VFR flights. To calculate the gallons needed for a Piper Archer, follow these steps:
1. Determine the fuel consumption rate of the Piper Archer at cruising speed, which is typically around 10 gallons per hour (GPH).
2. Divide the required fuel reserve minutes (30) by the minutes in an hour (60): 30 / 60 = 0.5 hours.
3. Multiply the fuel consumption rate (10 GPH) by the required fuel reserve time in hours (0.5 hours): 10 * 0.5 = 5 gallons.
Therefore, for a day VFR flight in a Piper Archer, you would need a fuel reserve of approximately 5 gallons.
learn more about "fuel reserve":-https://brainly.com/question/31663770
#SPJ11