Let f be a differentiable function with f(1) = 2, f'(1) = 3, f(-4)= -3, and
f'(-4)= 4. Let the function g(x) = f(2x - 6). Write the equation of the line
tangent to the graph of g at the point where x = 1.
Answers
The equation of the line tangent to the graph of g at the point where x = 1 y + 10x + 44 =0.
What is line tangent?
A line that touches a curve at one point is said to be tangent. A point of tangency is the location where a curve and a line intersect. Y = mx + b is the slope-intercept formula for a line, where m is the line's slope. The straight line that "just touches" the curve at a particular location is referred to as the tangent line to a plane curve in geometry. It was described by Leibniz as the path connecting two points on a curve that are infinitely near together.
Given g(x)=f(2x)
Differentiate it on both side with respect to x.
\(\begin{aligned}& \frac{d g(x)}{d x}=2 * \frac{d f(2 x)}{d x} \\& \frac{d g(-1)}{d x}=2 * \frac{d f(-8)}{d x}=-5^* 2=-10\end{aligned}\)
Slope =-10
Here x coordinate = -4
g(-4)=f(-8)=-4 = y coordinate
Thus point of tangency on function g is (-4,-4)
Thus equation of tangent is
y + 4= -10(x+4)
y + 10x + 44 =0
To learn more about Slope visit:https://brainly.com/question/3605446
#SPJ1
Answer:
y = 8x -11
Step-by-step explanation:
You want the equation of the line tangent to g(x) = f(2x-6) at x=1, where f is a differentiable function with f(1) = 2, f(-4) = -3, f'(1) = 3, f'(-4) = 4.
Tangent lineThe equation of the tangent line at x=1 can be written ...
y = g'(1)(x -1) +g(1)
The necessary function values are ...
g(1) = f(2·1 -6) = f(-4) = -3
and
g'(x) = f'(2x -6)·(2x -6)' = 2f'(2x -6)
g'(1) = 2f'(2·1 -6) = 2f'(-4) = 8
Then the equation of the line is ...
y = 8(x -1) +(-3) = 8x -8 -3
y = 8x -11 . . . . . . tangent to g(x) at x=1
__
Additional comment
The minimum polynomial function f(x) that can have the desired values and derivatives is a cubic. The attached graph shows g(x) and the tangent at x=1 using that cubic for f(x).

Related Questions
which statement describes a parallelogram that must be a square?
Answers
A parallelogram that must be a square can be described by the statement: "A parallelogram in which all angles are right angles (90 degrees) is a square."
In a parallelogram, opposite sides are parallel and congruent, and opposite angles are also congruent. However, for a parallelogram to be a square, it must have additional properties:
All angles are right angles: In a square, all four angles are equal and measure 90 degrees. This distinguishes a square from a general parallelogram where the angles can be acute or obtuse.
All sides are congruent: In a square, all four sides are equal in length. This equality of side lengths sets a square apart from a rectangular parallelogram, where only opposite sides are congruent.
Diagonals are congruent and bisect each other at right angles: The diagonals of a square are equal in length and intersect at right angles, dividing the square into four congruent right triangles.
To know more about parallelogram,
https://brainly.com/question/7099686
#SPJ11
Complete question:
Which statement describes a parallelogram that must be a square? A parallelogram with opposite sides that are congruent and diagonals that bisect the angles. A parallelogram with a right angle and diagonals that bisect the angles. A parallelogram with a right angle and opposites sides that are congruent. A parallelogram with all sides congruent.
What’s the answer help pls

Answers
a manufacture produces wood tables on an assembly line, currently producing 1600 tables per shift. If the production is increased to 2000 tables per shift, labor productivity will increase by?
A) 10%
B) 20%
C) 25%
D) 40%
Answers
If the production of wood tables on an assembly line increases from 1600 tables per shift to 2000 tables per shift, the labor productivity will increase by 25%.We need to determine the percentage change.
To calculate the increase in labor productivity, we need to compare the difference in production levels and determine the percentage change.The initial production level is 1600 tables per shift, and the increased production level is 2000 tables per shift. The difference in production is 2000 - 1600 = 400 tables.
To calculate the percentage change, we divide the difference by the initial production and multiply by 100:
Percentage Change = (Difference / Initial Production) * 100 = (400 / 1600) * 100 = 25%.
Therefore, the correct answer is option C) 25%, indicating that labor productivity will increase by 25% when the production is increased to 2000 tables per shift.
To learn more about percentage change click here : brainly.com/question/14979505
#SPJ11
Laura is saving to buy a 10-speed bike that costs $189. For four weeks she saved part of her check in the amounts of $15, $39, $18 and $27. How much more does she need?
Answers
Answer:
90$
Step-by-step explanation:
Answer:
$90
Step-by-step explanation:
$15 + $39 + $18 + $27 = $99
$189 - $99 = $90
Hope this helps <3
Help help help help help
Answers
Answer:
What can I answer ehh that's just an help ♀️♀️
ellie is learning to play dungeons and dragons. She wants to purchase dice and gaming books. Gaming books cost 40$ each and sets of dice cost 8$. Ellie wants to get at least two sets of dice and wants to spend no more than 80$. write a system of linear inequalities that represent the situation. Determine if the points are possible solutions.
Answers
Answer: 40G+8D ≤ 80; D must be at least 2 as stated in problem and can be up to 10, and you can have a maximum of 1 game book depending on how many dice sets you get (if you get more than 5 dice sets you cannot have any game books).
Step-by-step explanation: Since gaming books cost $40 so $40G for the amount of money spent and since sets of dice cost $8 so 8D for the money spent. Since the money spent must be less than or equal to 80 we put symbol at end.
Let X
1
,⋯,X
m
be i.i.d. N(μ
1
,σ
1
2
) observations, Y
1
,⋯,Y
n
be i.i.d. N(μ
2
,σ
2
2
) observations and let us further assume that the X
′
s and Y
′
s are mutually independent. (a) Assuming that σ
1
,σ
2
are known, find a confidence interval for μ
1
−μ
2
whose coverage probability is 1−α for a given α. (b) Assuming that both m,n are large, justify the use of
X
ˉ
−
Y
ˉ
±z
α/2
S
X
2
/m+S
Y
2
/n
as approximate 1−α confidence bounds for μ
1
−μ
2
.
Answers
The use of this approximation is justified when both m and n are large enough, typically greater than 30, where the CLT holds reasonably well and the sample means can be considered approximately normally distributed.
(a) To find a confidence interval for μ1 - μ2 with a coverage probability of 1 - α, we can use the following approach:
1. Given that σ1 and σ2 are known, we can use the properties of the normal distribution.
2. The difference of two independent normal random variables is also normally distributed. Therefore, the distribution of (xbar) - ybar)) follows a normal distribution.
3. The mean of (xbar) - ybar)) is μ1 - μ2, and the variance is σ1^2/m + σ2^2/n, where m is the sample size of X observations and n is the sample size of Y observations.
4. To construct the confidence interval, we need to find the critical values zα/2 that correspond to the desired confidence level (1 - α).
5. The confidence interval can be calculated as:
(xbar) - ybar)) ± zα/2 * sqrt(σ1^2/m + σ2^2/n)
Here, xbar) represents the sample mean of X observations, ybar) represents the sample mean of Y observations, and zα/2 is the critical value from the standard normal distribution.
(b) When both m and n are large, we can apply the Central Limit Theorem (CLT), which states that the distribution of the sample mean approaches a normal distribution as the sample size increases.
Based on the CLT, the sample mean xbar) of X observations and the sample mean ybar) of Y observations are approximately normally distributed.
Therefore, we can approximate the confidence bounds for μ1 - μ2 as:
(xbar) - ybar)) ± zα/2 * sqrt(SX^2/m + SY^2/n)
Here, SX^2 represents the sample variance of X observations, SY^2 represents the sample of Y observations, and zα/2 is the critical value from the standard normal distribution.
Note that in this approximation, we replace the population variances σ1^2 and σ2^2 with the sample variances SX^2 and SY^2, respectively.
To know more about probability visit:
brainly.com/question/31828911
#SPJ11
Answer to this question ?

Answers
Answer:
(x - 10)(x - 3)
Step-by-step explanation:
You have to think of numbers that multiply up to 30 and add up to 13. So you eliminate the numbers down to 10 and 3, because you can add up to 13 and multiply to 30. Now you have to find how it adds up to negative 13 and multiply it to postive 30. 2 negatives make a positive when multiplying, and 2 negatives added together make another negative, so your roots are 10 and 3. Put that into factored form and you have (x - 10)(x - 3).
Alternatively you can either graph to find its zeros or guess-and-check.
How many solution S does the system X 2y 3 3x 6y 9 have?
Answers
To find the number of solutions that the system x + 2y = 3 and 3x + 6y = 9 has, we can solve the system using various methods, such as graphing, substitution, or elimination.
What does the term "system of equations" mean?
A system of equations is a collection of two or more equations that are solved simultaneously. A solution to a system of equations is a set of values for the variables that makes all of the equations in the system true simultaneously.
One way to solve this system is to use the substitution method. We can solve the first equation for y and substitute the result into the second equation to obtain an equation in one variable.
x + 2y = 3
y = (3 - x) / 2
Substituting this expression for y into the second equation, we get:
3x + 6((3 - x) / 2) = 9
Simplifying the right-hand side, we get:
3x + 3 - 3x = 9
Combining like terms, we get:
0 = 9
This equation is not true for any value of x, so the system does not have a solution. As a result, the system is incoherent.
Learn more about system of equations
https://brainly.com/question/13729904
#SPJ4
5. In this diagram, lines AC and DE are parallel,
and line DC is perpendicular to each of them. If
segment BD has length , calculate the length of
side DE
Answers
The length of side DE is 3cm
Parallel lineSince the line AC is equivalent to DE, hence AC = DE
To get the length of DE, we will need to get the length oF AC using the Pythagoras theorem:
Given the following parameters
Hypotenuse = 5
Opposite = 4
Required
Adjacent side
Substitute the given parameters into the formula of Pythagoras theorem.
AC² = 5² - 4²
AC² = 25 - 16
AC² = 9
AC = 3
Hence the length of side DE is 3cm
Learn more on Pythagoras theorem here: https://brainly.com/question/12306722

Is the following data an example of a linear function?

Answers
Yes, The given table is an example of a linear function.
Since, The equation of line in point-slope form passing through the points
(x₁ , y₁) and (x₂, y₂) with slope m is defined as;
⇒ y - y₁ = m (x - x₁)
Where, m = (y₂ - y₁) / (x₂ - x₁)
We have to given that;
To check the following data an example of a linear function.
Now, We can check the slope of given tables as;
⇒ Slope = (3 - (- 2)) / (0 - (- 7))
= (5 / 7)
⇒ Slope = (8 - 3) / (7 - 0)
= (5 / 7)
Thus, This table represent the an example of a linear function.
Learn more about the equation of line visit:
https://brainly.com/question/18831322
#SPJ1
is the inverse of y=2^x a function?
Answers
The inverse of the function is equal to ln(x) - ln(2) = y.
What is the inverse of the function?The inverse function of a function f is a function that reverses the operation of f. The inverse of f exists if and only if f is bijective, and it is denoted by f⁻¹ if it exists.
Given that the function is \(y=2^x\). To get the inverse function just replace the variables x by y and then calculate the value of y.
The inverse of the function will be calculated as,
\(y = 2^x\)
\(x=2^y\)
Take logs on both sides,
ln(x) = yln(2)
ln(x) / ln(2) = y
y = ln(x) - ln(2)
The inverse is y = ln(x) - ln(2).
To know more about an inverse of the function follow
https://brainly.com/question/19425567
#SPJ1
Review Questions
1. Cindy is a baker and runs a large cupcake shop. She has already
a. How many workers will the firm hire if the market wage rate is
hired 11 employees and is thinking of hiring a 12th. Cindy esti- $27.95 ? \$19.95? Explain why the firm will not hire a larger or mates that a 12 th worker would cost her $100 per day in wages $ smaller number of units of labor at each of these wage rates. and benefits while increasing her total revenue from $2,600per. day to $2,750 per day. Should Cindy hire a 12 th worker? b. Show this firm Explain. L016.2 c. Now again determine the firm's demand curve for labor. Complete the following labor demand table for a firm that is assuming that it is selling in an imperfectly competitive marhiring labor competitively and selling its product in a competiket and that, although it can sell 17 units at $2.20 per unit, it tive market. L016.2 ginal product of each successive labor unit. Compare this demand curve with that derived in part b. Which curve is more elastic? Explain. 3. Alice runs a shoemaking factory that uses both labor and capital to make shoes. Which of the following would shift the factory's demand for capital? You can select one or more correct answers from the choices shown. LO16.3 a. Many consumers decide to walk barefoot all the time. b. New shoemaking machines are twice as efficient as older machines. c. The wages that the factory has to pay its workers rise due to an economywide labor shortage.
Answers
Cindy should hire the 12th worker as it would result in a net increase in profit, with additional revenue exceeding the cost of hiring. Insufficient information is provided to determine the demand curve for labor or compare its elasticity. Events that would shift the factory's demand for capital include new, more efficient machines and rising wages due to a labor shortage.
a. To determine whether Cindy should hire a 12th worker, we need to compare the additional revenue generated with the additional cost incurred. Hiring the 12th worker would increase total revenue by $150 ($2,750 - $2,600) per day, but it would also increase costs by $100. Therefore, the net increase in total profit would be $50 ($150 - $100). Since the net increase in profit is positive, Cindy should hire the 12th worker.
b. By hiring the 12th worker, Cindy can increase her total revenue from $2,600 per day to $2,750 per day. The additional revenue generated by the 12th worker exceeds the cost of hiring that worker, resulting in a net increase in profit.
c. To determine the firm's demand curve for labor, we need information about the marginal product of labor (MPL) and the wage rates. Unfortunately, this information is not provided, so we cannot complete the labor demand table or derive the demand curve for labor.
Without specific data or information about changes in the quantity of labor demanded and wage rates, we cannot determine which demand curve (from part b or c) is more elastic. The elasticity of the demand curve depends on the responsiveness of the quantity of labor demanded to changes in the wage rate.
The events that would shift the factory's demand for capital are:
a. New shoemaking machines being twice as efficient as older machines would increase the productivity of capital. This would lead to an increase in the demand for capital as the factory would require more capital to produce the same quantity of shoes.
b. The wages that the factory has to pay its workers rising due to an economy-wide labor shortage would increase the cost of labor relative to capital. This would make capital relatively more attractive and lead to an increase in the demand for capital as the factory may substitute capital for labor to maintain production efficiency.
The event "Many consumers decide to walk barefoot all the time" would not directly impact the demand for capital as it is related to changes in consumer behavior rather than the production process of the shoemaking factory.
Learn more about the demand curve at:
brainly.com/question/1139186
#SPJ11
The number of goldfish in a tank is 22, and the volume of the tank is 56 cubic feet. what is the density of the tank? 0.34 goldfish per cubic foot 0.39 goldfish per cubic foot 1.41 goldfish per cubic foot 2.55 goldfish per cubic foot
Answers
Option B is correct. 0.39 goldfish per cubic feet is the density of the tank given that there are 22 goldfishes and volume of the tank is 56 cubic feet. This can be obtained by using the formula of density.
Calculate the density of tank:Given that there are 22 goldfishes,
mass of tank = 22 goldfishes
volume of tank = 56 cubic feet
Density = mass/volume= 22/56
= 0.39 goldfish per cubic feet
Hence 0.39 goldfish per cubic feet is the density of the tank given that there are 22 goldfishes and volume of the tank is 56 cubic feet.
Learn more about density:
brainly.com/question/14762317
#SPJ1
Answer: 0.39 goldfish
Step-by-step explanation:
WILL BRAINLIST
45 points
Drag each tile to the correct box. Not all tiles will be used.
Simplify the expression by arranging the steps in sequence, based on the order of operations,

Answers
I need help with this!
Use your formula 1/2(a+b)h, to determine the height of a trapezoid with an area of 24 cubic centimeters and base lengths of 9 cm and 7 cm.
Answers
Answer:
H (Height) = 3
Step-by-step explanation:
We have the formula A = 1/2(a+b)h
Let's identify all variables
A = 24
a = 9
b = 7
h = ?
Lets plug all that in:
24 = 1/2(9+7)h
9+7 = 16
24 = 1/2(16)h
Half of 16 is 8 so to simplify the rest...
24 = 8h
To get h alone we will divide both sides of the equation by 8
24/8 = h
24/8 = 3
Making H = 3
A) A box of mass 9 kg contains x articles each of mass 1.2 kg. Write down an expression for the total mass of the box and its contents.
B) How many articles are there in the box if the total mass of the box and articles is 21 kg?
Answers
Step-by-step explanation:
A. total mass = 9 + (x × 1.2)
B. 21 - 9 = 12kg
12 ÷ 1.2 = 10 articles.
hope it helps. :)
A woman bought some large frames for $19 each and some small frames for $9 each at a closeout sale. If she bought 27 frames for $343, find how many of each type she bought.
Answers
Let x be the number of large frames and y be the number of small frames that a woman bought from the closeout sale.Therefore, the two equations that we can use to solve the problem are:
x + y = 27 ...(1)and19x + 9y = 343 ...(2)Multiplying equation (1) by 9 and subtracting it from equation (2), we get:19x + 9y = 343 ...(2)- (9x + 9y = 243) ...(3)10x = 100x = 10Thus, the woman bought 10 large frames
.Substituting x = 10 in equation (1), we get:10 + y = 27y = 27 - 10y = 17Thus, the woman bought 17 small frames. Therefore, the woman bought 10 large frames and 17 small frames.
To Know more about Substituting visit:
brainly.com/question/29383142
#SPJ11
Why is addition used to represent the submarine’s position changing from -8
feet to 0 feet below sea level?
What integer represents a submarine 8 feet below sea level?
What integer represents a submarine rising 8 feet?
Answers
-8ft (below from sea level)
8ft (above from sea level)
Please mark brainliest!!
Some History teachers at Booneville High School are purchasing tickets for students and their adult chaperones to go on a field trip to a nearby museum. For her class, Mrs. Warren bought 31 student tickets and 28 adult tickets, which cost a total of $842. Mr. Greer spent $792, getting 26 student tickets and 28 adult tickets. What is the price for each type of ticket?
Answers
By making and solving equations we know that the children's ticket costs $72.91 each and adult tickets cost $110.8 each.
What are equations?An equation is a mathematical statement that contains the symbol "equal to" between two expressions with identical values.
As in 3x + 5 = 15, for example.
There are many different types of equations, including linear, quadratic, cubic, and others.
So, solve as follows:
31c + 28a = 842 ...(1)
26c + 28a = 792 ...(2)
Now,
31c = 842 - 28a
c = 842 - 28a/31
Then,
26c + 28a = 792
26(842 - 28a/31) + 28a = 792
26(842 - 28a) + 28a = 24,552
21,892 - 52a + 28a = 24,552
21,892 - 24a = 24,552
24a = 24,552 - 21,892
24a = 2,660
a = 110.8
Now,
31c + 28a = 842
31c + 28(110.8) = 842
31c + 3,102.4 = 842
31c = 842 - 3,102.4
31c = 2,260.4
c = 72.91
Therefore, by making and solving equations we know that the children's ticket costs $72.91 each and adult tickets cost $110.8 each.
Know more about equations here:
https://brainly.com/question/2972832
#SPJ1
Find EF in the trapazoid

Answers
EF = 45
Step-by-step explanation:
Area if Trapezium = \(\frac{a + b}{2} h\)
Median = \(\frac{1}{2} (a + b)\)
Median = 5x
5x = 1/2 ((x + 3) + 78)
5x = (x + 81) / 2
10x = x + 81
9x = 81
x = 9
EF = 5x
EF = 5(9)
EF = 45
what do you think you’d like most about working as a forensic scientist? why
Answers
Answer:
i think its very interesting and pretty cool, because there is so much to learn and so much to explore
i wouldn't like the fact that you have to study so much though
Step-by-step explanation:
Help,anyone can help me do quetion

Answers
Answer:
a3) x= 83
y= 180-71 = 109
a4) x=53
w= 180-53...
y=x=53
z= 180-y
In the following linear system, determine all values ofa for which the resulting linear system has
a) no solution;
b) a unique solution;
c) infinitely many solutions;
x+ y- z= 2
x+2y+ z= 3
x+ y+(a2 -5)z= a
Answers
a) The linear system has no solution when a ≠ 2 and a^2 - 4 = 0. b) The linear system has a unique solution when a ≠ 2 and a^2 - 4 ≠ 0. c) The linear system has infinitely many solutions when a = 2 and a^2 - 4 = 0.
To determine the values of "a" for which the linear system has no solution, a unique solution, or infinitely many solutions, we can analyze the augmented matrix and its row echelon form. Let's write the augmented matrix for the given linear system:
[1 1 -1 | 2]
[1 2 1 | 3]
[1 1 a^2-5| a]
Performing row operations to obtain the row echelon form:
R2 = R2 - R1
R3 = R3 - R1
[1 1 -1 | 2]
[0 1 2 | 1]
[0 0 a^2-4| a-2]
From the row echelon form, we can make the following observations:
1. If a^2 - 4 ≠ 0, then the linear system will have a unique solution. This is because there are no inconsistencies or contradictions in the row echelon form, and we can solve for all variables.
2. If a^2 - 4 = 0 and a ≠ 2, then the linear system will have no solution. This is because the row echelon form will have a row of zeros on the left side and a non-zero entry on the right side, indicating an inconsistency.
3. If a^2 - 4 = 0 and a = 2, then the linear system will have infinitely many solutions. This is because the row echelon form will have a row of zeros on the left side and a zero entry on the right side, indicating dependent equations and infinite solutions
a) The linear system has no solution when a ≠ 2 and a^2 - 4 = 0.
b) The linear system has a unique solution when a ≠ 2 and a^2 - 4 ≠ 0.
c) The linear system has infinitely many solutions when a = 2 and a^2 - 4 = 0.
To learn more about solutions click here:
brainly.com/question/30967647
#SPJ11
What is the height of the cylinder? The figure is not drawn to scale.
V = 282.7 in²
18 in
11.3 in
7.2 in
3.6 in

Answers
The height of the cylinder is \(3 inch\)
How can the height of the cylinder be found?Based on the attached figure,
Volume of the cylinder = 282.7 square inches
Radius of the cylinder =5 inches.
The height of the cylinder = ?
The volume of the cylinder can be found with the formula as :
\(V=pi r^{2} h\)
\(h=\frac{V}{pi r^{2} } \\\\h = \frac{282.7}{3.142 * 5^{2} } \\\\=3 inch\)
Learn more about cylinder at:
https://brainly.com/question/9554871
#SPJ1
when i divide 48 by the sum of 5 and a certain number, the result is 3. What is the number
Answers
Answer:
Let's first turn this into an equation. We are told 48 divided by the sum of 5 and a certain number we will call x equals three. This gives:
48/5+3 = 3
From here, we just need to isolate and solve for x. This is done as follows:
1) Multiply (5+x) by both sides to get it out of the denominator:
48=3(5+x)
2) Distribute the three to the binomial:
48=15+3x
3) Subtract 15 from both sides:
33=3x
4) Divide both sides by 3:
x=11
Finally verify we are correct by dividing 48 by 16 (the sum of 5 and x, our solution) to get 3.
Step-by-step explanation:
BRAINLIEST?
geometric? what does it mean and plz give a example
Answers
Answer:
of, relating to, or according to the methods or principles of geometry
increasing in a geometric progression.
the study of properties of given elements that remain invariant under specified transformations
explanation:
Hope this helps?
Please mark me as brainliest answerer?
I need it.
Find and sketch the domains of the following functions: (a) f(x,y) = √ 5 −2x+√16-y^2 +2
(b) g(x,y) =(e^x^y)/√1+y-x
(c) h(x,y) = √ −x−y /ln(1 − x)
2. Use the Taylor polynomial of degree 5 to approximate 4cos(0.1).
Answers
The domains of the given functions are as follows: (a) f(x,y) is defined for all real values of x and y. (b) g(x,y) is defined for all real values of x and y except when y = 1-x. (c) h(x,y) is defined for all real values of x and y such that x < 1 and x ≠ 1. The Taylor polynomial of degree 5 is used to approximate the value of 4cos(0.1).
Let's analyze each function and find their domains:
(a) f(x, y) = √(5 - 2x + √(16 - \(y^2\)))
For the square root to be defined, the expression inside the square root must be non-negative. Hence, we have two conditions:
1. 5 - 2x + √(16 - \(y^2\)) ≥ 0
Solving this inequality, we get: √(16 - \(y^2\)) ≥ 2x - 5
To ensure the square root is defined, we need 16 - y^2 ≥ 0, which means -4 ≤ y ≤ 4.
2. 16 - \(y^2\) ≥ 0
Solving this inequality, we get: -4 ≤ y ≤ 4.
Combining both conditions, we find that the domain of f(x, y) is:
-4 ≤ y ≤ 4 and 2x - 5 ≤ √(16 - \(y^2\))
(b) g(x, y) = \(e^{(x^y) }\)/ √(1 + y - x)
The exponential function is defined for all real numbers, so there are no restrictions on x and y for \(e^{(x^y) }\) to be defined.
For the square root to be defined, the expression inside the square root must be non-negative. Hence, we have the condition:
1 + y - x ≥ 0
Simplifying, we get: y ≥ x - 1.
Therefore, the domain of g(x, y) is all real numbers where y ≥ x - 1.
(c) h(x, y) = √(-x - y) / ln(\((1 - x)^2\))
For the square root to be defined, -x - y must be non-negative, so we have the condition:
-x - y ≥ 0
Simplifying, we get: y ≤ -x.
For the natural logarithm to be defined, the denominator must be greater than 0. Hence, we have the condition:
\((1 - x)^2\) > 0
This condition is always satisfied since\((1 - x)^2\)is always positive, so no additional restrictions on the domain are imposed.
Therefore, the domain of h(x, y) is y ≤ -x.
Now let's move on to the second part of the question:
To approximate 4cos(0.1) using a Taylor polynomial of degree 5, we need to evaluate the polynomial expansion of cos(x) centered at x = 0 up to the fifth degree.
The Taylor polynomial for cos(x) up to degree 5 is given by:
cos(x) ≈ 1 - (\(x^{2}\))/2! + (\(x^4\))/4!
Plugging in x = 0.1 into the polynomial, we have:
cos(0.1) ≈ 1 - (\(0.1^2\))/2! + (\(0.1^4\))/4!
Evaluating the expression, we get:
cos(0.1) ≈ 1 - (0.01)/2 + (0.0001)/24
Simplifying further:
cos(0.1) ≈ 1 - 0.005 + 0.0000041667
cos(0.1) ≈ 0.9950041667
Therefore, using the Taylor polynomial approximation of degree 5, 4cos(0.1) is approximately equal to 3.9800166668.
Learn more about Taylor polynomial here:
https://brainly.com/question/32592909
#SPJ11
Given f(x) = (x - 1)(x + 2)(x − 3), what are the zeros and end behavior of the function?
Answers
A function assigns the value of each element of one set to the other specific element of another set. The zeroes of the functions are -2, 1, and 3.
What is a Function?A function assigns the value of each element of one set to the other specific element of another set.
Given f(x) = (x - 1)(x + 2)(x − 3), therefore, the zeroes of the functions are -2, 1, and 3. The end behavior of the function is that if x approaches ∞ then f(x) approaches ∞, while if x approaches -∞ then f(x) approaches -∞, as can be observed from the given graph.
Hence, the zeroes of the functions are -2, 1, and 3.
Learn more about Function:
https://brainly.com/question/5245372
#SPJ1
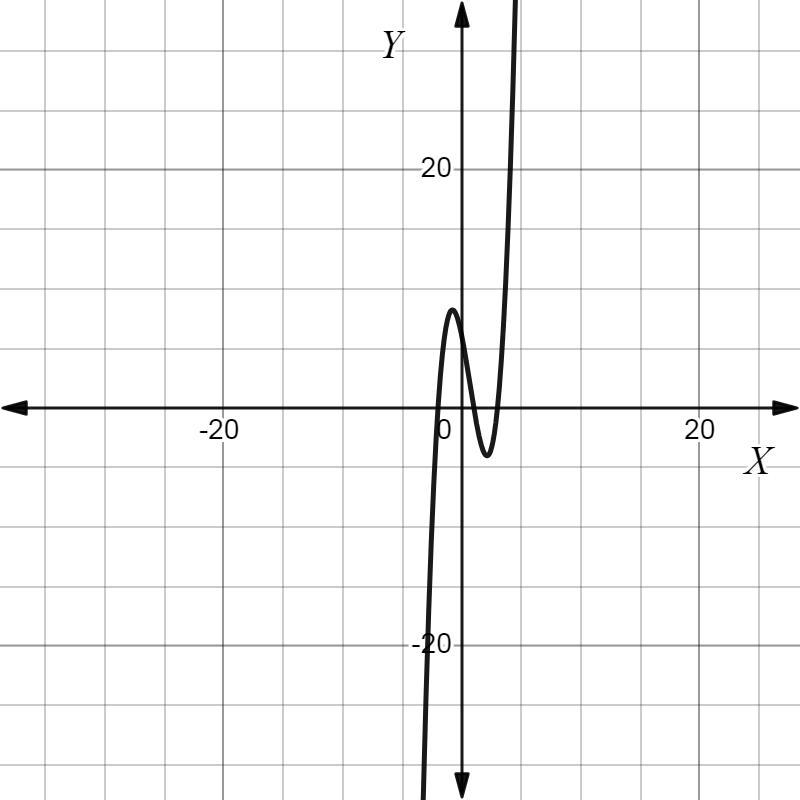
Answer:
−1, 2, −3; continues downward to the left and upward to the right
Step-by-step explanation:
A spring has a mass of 2 units, a damping constant of 6 units, and a spring constant of 30 units. If the spring is extended 2 units and then released with a velocity of 2 units. A forcing function of δ 2
(t) is applied to the spring. Answer the following. 6) A spring has a mass of 2 units, a damping constant of 6 units, and a spring constant of 30 units. If the spring is extended 2 units and then released with a velocity of 2 units. A forcing function of δ 2
(t) is applied to the spring. Answer the following.
Answers
a) The equation of motion for the spring with the given parameters is:
2 * x'' + 6 * x' + 30 * x = δ 2(t)
b) The natural frequency (ω) of the spring-mass system can be calculated using the formula:
ω = sqrt(k / m) = sqrt(30 / 2) = sqrt(15) ≈ 3.87 rad/s
c) The damping ratio (ζ) of the system can be calculated using the formula:
ζ = c / (2 * sqrt(k * m)) = 6 / (2 * sqrt(30 * 2)) ≈ 0.516
d) The type of damping in the system can be determined based on the damping ratio (ζ). Since ζ < 1, the system has underdamped damping.
e) The homogeneous solution of the system can be expressed as:
x_h(t) = e^(-ζωt) * (A * cos(ωd * t) + B * sin(ωd * t))
f) The particular solution of the system due to the forcing function δ 2(t) can be expressed as:
x_p(t) = K * δ 2(t)
g) The general solution of the system is given by the sum of the homogeneous and particular solutions:
x(t) = x_h(t) + x_p(t) = e^(-ζωt) * (A * cos(ωd * t) + B * sin(ωd * t)) + K * δ 2(t)
h) The values of A, B, and K can be determined using initial conditions and applying the appropriate derivatives.
a) The equation of motion for the spring-mass system is derived by applying Newton's second law, considering the mass, damping, and spring constant.
b) The natural frequency of the system is determined by the square root of the spring constant divided by the mass.
c) The damping ratio is calculated by dividing the damping constant by twice the square root of the product of the spring constant and mass.
d) Based on the damping ratio, the type of damping can be determined as underdamped, critically damped, or overdamped. In this case, since the damping ratio is less than 1, the system is underdamped.
e) The homogeneous solution represents the free vibration of the system without any external forcing. It contains exponential decay and sinusoidal terms based on the damping ratio and natural frequency.
f) The particular solution accounts for the response of the system due to the applied forcing function δ 2(t).
g) The general solution is obtained by adding the homogeneous and particular solutions together.
h) The specific values of the coefficients A, B, and K can be determined by considering the initial conditions of the system and applying the appropriate derivatives.
Learn more about spring-mass systems: brainly.com/question/31950988
#SPJ11