Last month, Curtis bought a new mountain bike for $250. In a store advertisement, the mountain bike is on sale for $210. What is the percent of the decrease in the value of the mountain bike?
Answers
Answer:
16%
Step-by-step explanation:
say the percent decrease = x. Then
x/100 x 250 = 210.
x/2 x 5 = 210
x/2 = 210/5
x/2 = 42
x = 42 x 2
x = 84.....
BUT this is not the answer. We need 100-84=16 for the answer.
So the bike dropped 16%. Thank me later :)
If Curtis bought a new mountain bike for $250. In a store advertisement, the mountain bike is on sale for $210. Then 16% of the decrease in the value of the mountain bike
What is Percentage?percentage, a relative value indicating hundredth parts of any quantity
Given,
Curtis bought a new mountain bike for $250.
the mountain bike is on sale for $210.
We need to find the percent of the decrease in the value of the mountain bike.
Let the percent decrease be x.
x/100 x 250 = 210.
5x/2= 210
Divide both sides by five
x/2 = 210/5
x by two equal to two ten by 5, we get x by two equal to forty two
x/2 = 42
Apply cross multiplication
x = 42 x 2
x = 84.
We need 100-84=16.
Hence 16 percent of the decrease in the value of the mountain bike
To learn more on Percentage click:
https://brainly.com/question/28269290
#SPJ2
Related Questions
According to a National Center for Health Statistics, the lifetime odds in favor of dying from heart disease are 1 to 5, so the probability of dying from heart disease is
Answers
Answer:
The probability of dying from heart disease based on the given information is 1/6 or approximately 0.1667. This is because the odds in favor of dying from heart disease are 1 to 5, which means there is 1 chance of dying from heart disease for every 5 chances of not dying from heart disease. To convert odds to probability, we divide the number of chances of the event occurring by the total number of chances. So, the probability of dying from heart disease is 1/(1+5) = 1/6 or approximately 0.1667.
NEED HELP
|w| + 19 < 14

Answers
the solution is: \(w < -5\) . Since all real numbers are either less than or greater than \(-5\) , the solution set for this inequality is "All reals".
What is the parameter for the real number?To solve for w in \(w + 19 < 14\) , we need to isolate w on one side of the inequality.
This means that any value of w that is less than \(-5\) would make the inequality true.
For example, \(w = -6\) is a solution because \(-6 + 19 < 14.\) Likewise, any value of w that is greater than or equal to -5 would make the inequality false. For example, \(w = -5\) is not a solution because \(-5 + 19 = 14\) .
Subtracting 19 from both sides of the inequality, we get:
\(w + 19 - 19 < 14 - 19\)
\(w < -5\)
Therefore, the solution is: \(w < -5\) . Since all real numbers are either less than or greater than \(-5\) , the solution set for this inequality is "All reals".
Learn more about number here:
https://brainly.com/question/551408
#SPJ1
m.
x-intercept =
1/2
and y-intercept = 3
Write an equation for the line in point-slope form and in slope-intercept form
Answers
Answer:
slope intercept form: y= -6x+3
point slope form: y-0= -6(x -1/2)
Step-by-step explanation:
point slope form: y - y1 = m(x - x1)
substitute the values y-0=-6(x-1/2)
slope intercept form:
find the slope using two given points
m = (y2 - y1) / (x2 - x1)
= (3 - 0) / (0 - 1/2)
= 3 / (-1/2)
= -6
substitute into equation
y= -6x+3
Which three relations are functions? Select all correct answers

Answers
Answer:
the 3rd, 4th, and 5th one
Step-by-step explanation:
Answer:
Step-by-step explanation:
:)

The following data give the distribution of the types of houses in a town containing 25,000 houses. Identify each category and its percentage on the circle graph. House Style Frequency Cape 6250 Garrison 10000 Split 8750
Answers
The categories and their Percentages on the circle graph would be as follows:
Cape: 25%
Garrison: 40%
Split: 35%
To represent the distribution of house types in a town containing 25,000 houses on a circle graph, we need to determine the percentage of each category.
The given data provides the following frequencies for each house style:
Cape: 6,250 houses
Garrison: 10,000 houses
Split: 8,750 houses
To calculate the percentage for each category, we divide the frequency of each house style by the total number of houses in the town (25,000) and multiply by 100.
Percentage for Cape: (6,250 / 25,000) * 100 = 25%
Percentage for Garrison: (10,000 / 25,000) * 100 = 40%
Percentage for Split: (8,750 / 25,000) * 100 = 35%
Therefore, the categories and their respective percentages on the circle graph would be as follows:
Cape: 25%
Garrison: 40%
Split: 35%
These percentages represent the proportion of each house style in the town and can be visually represented on a circle graph to provide a clear visualization of the distribution of house types.
To know more about Percentages.
https://brainly.com/question/24877689
#SPJ11

If a product normal retails for $40, and a customer has a coupon for 15% off, what will the discounted price of the product be?
Answers
Answer:
$34
Step-by-step explanation:
price of the product = $40
coupon = 15% off
discount price = 15% of price of a product
=15/100 * $40
=$600/100
=$6
New price of the product = original price - discount
=$40 - $6
=$34
What is the rental cost? Step by step.

Answers
The rental cost in dollars per square foot is $11,00
What is the rental cost in dollars per square foot?Cost of renting 1.250 square feet = $13, 750 per month
Rental cost per square foot = Total renting cost / total renting area
= $13, 750 per month / 1.250 square feet
= $11,000
Hence, $11,000 is the rental cost in dollars per square foot.
Read more on rental cost:
https://brainly.com/question/11959610
#SPJ1
Solve for x:
2x + 3 = 7
Answers
Answer:
x = 2
Step-by-step explanation:
First, subtract 3 from both sides.
2x + 3 = 7
- 3 -3
2x = 4
Then, divide both sides by 2.
2x / 2 = 4 / 2
x = 2
Answer:
the solution for x is x = 2
Step-by-step explanation:
To solve for x, we need to get x by itself on one side of the equation. First, we can subtract 3 from both sides to get:
2x + 3 - 3 = 7 - 3
Simplifying the left side gives us:
2x = 4
Then, we can divide both sides by 2 to get:
2x / 2 = 4 / 2
Simplifying the left side gives us:
x = 2
I really need help is there any one that can help me rn ?

Answers
Given:
a function f(x) = (x-2)^2 is given.
Find:
we have to find the function whose graph is a result of horizonal shift of 2 units of the original graph.
Explanation:
Since the given graph of the function is shifted 2 units horizontally,
and we know y is vertical axis, x is horizontal axis.
So put x = x+2 in the given function, we get
\(\begin{gathered} f(x)=(x+2-2)^2 \\ f(x)=x^2 \end{gathered}\)Therefore the graph of f(x)=(x-2)^2 is a result of horizontal shift of 2 units of f(x) = x^2.
The graphs are given for the reference

Drag the tiles to the correct boxes to complete the pairs. Match each function to its domain and range.

Answers
Matching of the functions domain and range are as follows:
f(x) = 4-4x ;
Domain:{0,1,3,5,6}
Range;{-20,-16,-8,0,4}
f(x) = 5x - 3
Domain:{-2,-1,0,3,4}
Range:{-13,-8,-3,12,4}
f(x) = -10x
Domain:{-4,-2,0,2,4}
Range:{-40,-20,0,20,40}
f(x) = (3/x) + 1.5
Domain:{-3,-2,-1,2,6}
Range:{0.5,0,-1.5,3,2}.
How to find the domain and range of the functions?1) The function f(x) = 4 - 4x
Take Domain:{0,1,3,5,6}
If, we take x=0 and put in the function then we get
f(x)=4-0
f(x)=4
put x=1
f(x) = 4 - 4 =0
put x=3 then we get
f(x)=4-12=--8
put x=5 them we get
f(x)=4-20=-16
put x=6 then we get
f(x)=4-24=-20
Therefore ,range:[-20,-16,-8,0,4}
2) The function f(x)=5x-3
Take domain{-2,-1,0,3,4}
Now, put x=-2 in the function then we get
f(x) = -13
now put x=-1 then we get
f(x)=-5-3=-8
Put x=0 then we get
f(x)=0-3=-3
Put x=3 then we get
f(x)=15-3=12
Put x=4 then we get
f(x)=20-3=17
Therefore , range:{-13,-8,-3,12,17}
3) The function f(x)=-10x
Take domain:{-4,-2,0,2,4}
Put x=-4 in the function then we get
f(x)=40
Put x= -2 then we get
f(x)=20
Put x=0 then we get
f(x)=0
Put x=2 then we get
f(x)=-20
Put x=4 then we get
f(x)=-40
Therefore , range :{-40,-20,0,20,40}
4) The function f(x)= (3/x) + 1.5
Take domain:{-3,-2,-1,2,6}
Put x= -3 in the taken function then we get
f(x)=-1+1.5=0.5
put x=-2 then we get
f(x)= -1.5+1.5=0
Put x=-1 then we get
f(x)=-3+1.5=-1.5
Put x= 2 then we get
f(x)=1.5+1.5=3
Put x= 6 then we get
f(x)=0.5+1.5=2
Therefore, range : {0.5,0,-1.5,3,2}.
Read more about Domain and Range at: https://brainly.com/question/10197594
#SPJ1
Which pair of expressions are equivalent?
A
3x+2+2x and 7x
B
8(x−3) a
nd 8x−24
C
4(x+1) and 4x+1
D
3(5x) and 8x
Answers
Layla borrowed some money from her friend in order to help buy a new video game
system. Layla agreed to pay the friend back some amount every week until her loan
was paid off. Let L represent the amount Layla owes her friend after t weeks. A graph
of L is shown below. Write an equation for I then state the y-intercept of the graph
and determine its interpretation in the context of the problem.

Answers
The linear equation for this scenario is L = -20t + 140. Layla owes her friend $140 and pays the friend $20 per week.
What is an equation?An equation consists of numbers and variables linked together by mathematical operations to form an expression.
A linear equation is in the form:
y = mx + b
Where m is the rate of change and b is the initial value
Let L represent the amount Layla owes her friend after t weeks.
Using the point from the graph (0, 140) and (7, 0):
L - 140 = [(0 - 140)/(7 - 0)](t - 0)
L - 140 = -20t
L = -20t + 140
The y intercept is 140
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
This is due in like a hour please help!

Answers
Answer:
i think the fourth one is equvilent ratio
Step-by-step explanation:
The mean resting pulse rate for men is 72 beats per minute. A simple random sample of men who regularly work out at Mitch's Gym is obtained and their resting pulse rates (in beats per minute) are listed below. Use a 0.05 significance level to test the claim that these sample pulse rates come from a population with a mean less than 72 beats per minute. Assume that the standard deviation of the resting pulse rates of all men who work out at Mitch's Gym is known to be 2.6 beats per minute. Use the critical value method of testing hypotheses. 87 89 69 63 70 65 88 84 58 53 66 70Ho= H1=Critical value=P Value=Test Value=
Answers
Answer:
We conclude that the mean resting pulse rate for men is 72 beats per minute.
Step-by-step explanation:
We are given that he mean resting pulse rate for men is 72 beats per minute. Assume that the standard deviation of the resting pulse rates of all men who work out at Mitch's Gym is known to be 2.6 beats per minute.
A simple random sample of men who regularly work out at Mitch's Gym is obtained and their resting pulse rates (in beats per minute) are listed below;
87, 89, 69, 63, 70, 65, 88, 84, 58, 53, 66, 70.
Let \(\mu\) = mean resting pulse rate for men.
SO, Null Hypothesis, \(H_0\) : \(\mu\) = 72 beats/minute {means that the mean resting pulse rate for men is 72 beats per minute}
Alternate Hypothesis, \(H_A\) : \(\mu\) < 72 beats/minute {means that the mean resting pulse rate for men is less than 72 beats per minute}
The test statistics that would be used here One-sample z-test statistics as we know about population standard deviation;
T.S. = \(\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }\) ~ N(0,1)
where, \(\bar X\) = sample mean mean resting pulse rate = \(\frac{\sum X}{n}\)
= \(\frac{87+ 89+ 69 +63 +70 +65+ 88+ 84+ 58+ 53+ 66+ 70}{12}\) = 71.83 beats/minute
\(\sigma\) = population standard deviation = 2.6 beats per minute
n = sample of men = 12
So, the test statistics = \(\frac{71.83 - 72}{\frac{2.6}{\sqrt{12} } }\)
= -0.23
The value of z test statistics is -0.23.
Also, P-value of the test statistics is given by;
P(Z < -0.23) = 1 - P(Z \(\leq\) 0.23)
= 1 - 0.59095 = 0.40905
Now, at 0.05 significance level the z table gives critical value of -1.645 for left-tailed test.
Since our test statistic is more than the critical value of z as -0.23 > -1.645, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.
Therefore, we conclude that the mean resting pulse rate for men is 72 beats per minute.
PLEASEE HELPP ASAP!
Consider a right triangle which is
changing shape in the following
way. The horizontal leg is
increasing at the rate of 11 in/min
and the vertical leg is decreasing
at the rate of 5 in/min. At what rate <
is the hypotenuse changing in
in/min when the horizontal leg is 12
inches and the vertical leg is 9
inches?
Answers
Answer:
Step-by-step explanation:
GIVEN: dx / dt=5 in./min. and dy/ dt=−6 in./min.
FIND: dz/ dt when x=12 in. and y=9 in.
Use the Pythagorean Theorem to get the equation
x2+y2=z2
Now differentiate this equation with repect to time t getting
D{x2+y2}=D{z2} ⟶
2xdxdt+2ydydt=2zdzdt ⟶
(Multiply both sides of the equation by 1/2.)
x dx/ dt+y dy/ dt= z dz/ dt (DE)
Now let x=12 and y=9 and solve for z using the Pythagorean Theorem.
tex2html_wrap_inline125
122+92=z2 ⟶ z2=225 ⟶ z=15
Plug in all given rates and values to the equation (DE) getting
(12)(5)+(9)(−6)=(15)dz/ dt ⟶
6=15dzdt ⟶
dz/ dt=615=25 in/min.
Hope this answer helps you :)
Have a great day
Mark brainliest
Evaluate each expression for n= -5.
5. n-6
6.-15-n
7. n-(-12)
8. 1-n

Answers
Answer:
Hello!
5: -11
6: -10
7: 7
8: 6
Hope that helps!
A family decides to put tiles in the entryway of their home. The entryway has an area of 7 square meters. If each tile is 5 centimeters by 5 centimeters, how many tiles will it take to cover the entryway?
It will take ______ tiles to cover the entryway.
Answers
9514 1404 393
Answer:
2800 tiles
Step-by-step explanation:
Each tile has an area of (0.05 m)² = 0.0025 m². Then the number of tiles required to cover 7 square meters is ...
(7 m²)/(0.0025 m²/tile) = 2800 tiles
It will take 2800 tiles to cover the entryway.
Find the missing angels 25x+x=90
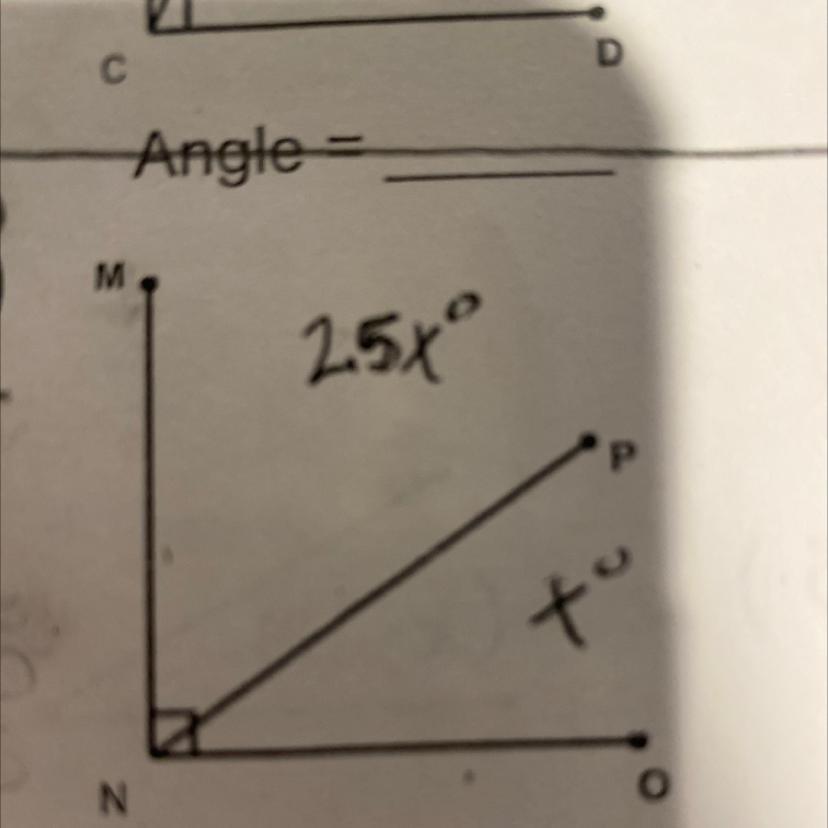
Answers
Answer:
3.46°
Step-by-step explanation:
25x°+x°=90°
26x°=90°
x°=90°/26°
x°=3.46°
The residual plot shows the residuals for the day of the month and the amount in Kali’s checking account. Which statement best assesses the linearity of the relationship between the day of the month and account balance if the scatterplot appears to be reasonably linear?
A) Because the residual plot has an obvious pattern, and the scatterplot appears linear, it is appropriate to use the line of best fit to predict the account balance based on the day of the month.
B) Because the residual plot has an obvious pattern, and the scatterplot appears linear, it is not appropriate to use the line of best fit to predict the account balance based on the day of the month.
C) Because the residual plot has no obvious pattern, and the scatterplot appears linear, it is appropriate to use the line of best fit to predict the account balance based on the day of the month.
D) Because the residual plot has no obvious pattern, and the scatterplot appears linear, it is not appropriate to use the line of best fit to predict the account balance based on the day of the month.
Answers
The best assessment of the linearity of the relationship between the day of the month and account balance would be "Because the residual plot has no obvious pattern, and the scatterplot appears linear, it is appropriate to use the line of best fit to predict the account balance based on the day of the month."The correct answer is option C.
When assessing linearity, it is important to examine both the scatterplot and the residual plot. The scatterplot is used to visualize the relationship between the variables, while the residual plot helps us assess the appropriateness of a linear model by examining the pattern of the residuals (the differences between observed and predicted values).
If the scatterplot appears reasonably linear, it suggests that there is a linear relationship between the variables. In this case, since the scatterplot appears linear, it supports the use of a linear model to predict the account balance based on the day of the month.
Furthermore, the residual plot is used to check for any patterns or systematic deviations from the line of best fit. If the residual plot exhibits no obvious pattern and the residuals appear randomly distributed around zero, it indicates that the linear model captures the relationship adequately.
Therefore, if the residual plot shows no obvious pattern, it provides further evidence in favor of using the line of best fit to predict the account balance based on the day of the month.
In conclusion, when the scatterplot appears linear and the residual plot shows no obvious pattern, it is appropriate to use the line of best fit to predict the account balance based on the day of the month.
For more such questions on linearity,click on
https://brainly.com/question/2030026
#SPJ8
Answer:
person above
Step-by-step explanation:
the obvious

which property of exponents must you apply to the express p 1/2 to derive p as the result
Answers
The expression becomes: p^(1/2) = p^(1/2 * 1) = p^(1/2) Now we can simplify p^(1/2) as p^1/2 which equals the square root of p.
The property of exponents that must be applied to the expression p^(1/2) to derive p as the result is the Power of a Power Property.
The Power of a Power Property states that when a power is raised to another power, the exponents are multiplied.
For instance, consider the expression p^(1/2). We can apply the Power of a Power Property to this expression as follows: p^(1/2) = (p^(1/2))^1 By applying the Power of a Power Property, the exponent (1/2) is multiplied by the exponent 1, giving a result of 1/2.
Therefore, the expression becomes: p^(1/2) = p^(1/2 * 1) = p^(1/2)Now we can simplify p^(1/2) as p^1/2 which equals the square root of p.
So we have derived p as the result using the Power of a Power Property.
In summary, we must apply the Power of a Power Property to the expression p^(1/2) to derive p as the result.
For more such questions on square root
https://brainly.com/question/428672
#SPJ8
"What are the coordinates of your reflected triangle A’B’C’?"
Please help! Thank you!

Answers
A' - (-1,4)
B' - (-1,8)
C' - (-5,4)
hope this helps
Determine the equation of the parabola that opens to the right, has focus (13,-6),
and a focal diameter of 28.
Answers
The equation of the parabola is\((y + 6)^2 = 4(x - 13)\), where the vertex is (13, -6) and the distance between the directrix and focus is 14.
To determine the equation of the parabola, we need to use the standard form for a parabola with a horizontal axis:
\((x - h)^2 = 4p(y - k)\)
Where (h, k) represents the vertex of the parabola, and p is the distance from the vertex to the focus (and also from the vertex to the directrix).
Given that the parabola opens to the right, the vertex will be on the left side. Let's assume the vertex is (h, k).
We know that the focus of the parabola is at (13, -6), so the distance from the vertex to the focus is p = 13 - h.
We are also given that the focal diameter is 28, which means the distance between the directrix and the focus is twice the distance from the vertex to the focus.
Therefore, the distance from the vertex to the directrix is d = 28/2 = 14.
for such more question on parabola
https://brainly.com/question/18274774
#SPJ11
Evaluate |x - y| + 4 if x = -1, y = 3, and z = -4.
Answers
Answer:
8
Step-by-step explanation:
Substitute the values in the expression, we have:
\(\displaystyle{|-1-3|+4}\)
Evaluate:
\(\displaystyle{|-4|+4}\)
Any real numbers in the absolute sign will always be evaluated as positive values. Thus:
\(\displaystyle{|-4|+4 = 4+4}\\\\\displaystyle{=8}\)
Hence, the answer is 8. A quick note that z-value is not used due to lack of z-term in the expression.
WILL G8VE BRAINLIEST IF YOU ARE CORRECT!!!
What is the decimal equivalent of 147/60
A. 2.27
B. 2.40
C. 2.45
D. 2.50
Answers
A model rocket is launched with an initial upward velocity of 183 ft/s. The rocket's height h (in feet) after t seconds is given by the following.
h=183t-16t^2
Find all values of t for which the rocket's height is 95 feet.
Answers
Answer:
0.55 seconds and 10.89 seconds
Step-by-step explanation:
h = 183t − 16t²
95 = 183t − 16t²
16t² − 183t + 95 = 0
Solve with quadratic formula:
t = [ -(-183) ± √((-183)² − 4(16)(95)) ] / 2(16)
t = (183 ± √27409) / 32
t = (183 ± √27409) / 32
t ≈ 0.55 or 10.89
How do you solve this question? Is it possible- or what do you add to make it possible?

Answers
Answer:
x = 90°
Step-by-step explanation:
We assume that angle x° is measured to a tangent to the circle.
__
The angle between a radius and the tangent to a circle is always 90°.
x = 90°
A ball is thrown straight down from the top of a 435-foot building with an initial velocity of -27 feet per second. Use the position function below for free-falling objects. s(t) = -16t^2 + v_0t + s_0 What is its velocity after 2 seconds? v(2) = -91 ft/s What is its velocity after falling 364 feet? v = 1.61 ft/s Find an equation of the parabola y = ax^2 + bx + c that passes through (0, 1) and is tangent to the line y = 5x - 5 at (1, 0). Y = 5x + 10
Answers
Answer:
a) The velocity of the ball after 2 seconds is -91 feet per second, b) The velocity of the ball after falling 364 feet is 155 feet per second, c) The equation of the parabola that passes through (0,1) and is tangent to the line y = 5x - 5 is \(y = 6\cdot x^{2}-7\cdot x +1\).
Step-by-step explanation:
a) The velocity function is obtained after deriving the position function in time:
\(v (t) = -32\cdot t -27\)
The velocity of the ball after 2 seconds is:
\(v(2\,s) = -32\cdot (2\,s) -27\)
\(v(2\,s) = -91\,\frac{ft}{s}\)
The velocity of the ball after 2 seconds is -91 feet per second.
b) The time of the ball after falling 364 feet is found after solving the position function as follows:
\(435\,ft - 364\,ft = -16\cdot t^{2}-27\cdot t + 435\,ft\)
\(-16\cdot t^{2} - 27\cdot t + 364 = 0\)
The solution of this second-grade polynomial is represented by two roots:
\(t_{1} = 4\,s\) and \(t_{2} = -5.688\,s\).
Only the first root is physically reasonable since time is a positive variable. Now, the velocity of the ball after falling 364 feet is:
\(v(4\,s) = -32\cdot (4\,s) - 27\)
\(v(4\,s) = -155\,\frac{ft}{s}\)
The velocity of the ball after falling 364 feet is 155 feet per second.
c) Let consider the equation for a second order polynomial that passes through (0, 1) and its first derivative that passes through (1, 0) and represents the give equation of the tangent line. That is to say:
Second-order polynomial evaluated at (0, 1)
\(c = 1\)
Slope of the tangent line evaluated at (1, 0)
\(5 = 2\cdot a \cdot (1) + b\)
\(2\cdot a + b = 5\)
\(b = 5 - 2\cdot a\)
Now, let evaluate the second order polynomial at (1, 0):
\(0 = a\cdot (1)^{2}+b\cdot (1) + c\)
\(a + b + c = 0\)
If \(c = 1\) and \(b = 5 - 2\cdot a\), then:
\(a + (5-2\cdot a) +1 = 0\)
\(-a +6 = 0\)
\(a = 6\)
And the value of b is: (\(a = 6\))
\(b = 5 - 2\cdot (6)\)
\(b = -7\)
The equation of the parabola that passes through (0,1) and is tangent to the line y = 5x - 5 is \(y = 6\cdot x^{2}-7\cdot x +1\).
SSA does not guarantee congruence between two triangles true or false?
Answers
Answer:
FALSEStep-by-step explanation:
SSA=S = Side
S = Side
A = Angle
It does not guarantee congruence between two Triangles due to the fact that the Angles are not included between two sides or Angle(A) should be Replaced by Side(S) in SSA axiom of congruence of two triangles.
It is a true statement that;"SSA does not guarantee congruence between two triangles ".
Congruence of triangles?The congruence of triangles can be based on certain rules such as; SSS, SAS, ASA, and AAS. This are the valid rules that guide the congruence of triangles.
Having said that, it the follows that it is a true statement that;"SSA does not guarantee congruence between two triangles ".
Learn more about congruence: https://brainly.com/question/1010345
#SPJ5
A Norman window has the shape of a rectangle surmounted by a semicircle. Suppose the outer perimeter of such a window must
be 600 cm. In this problem you will find the base length a which will maximize the area of such a window. Use calculus to find
an exact answer.
When the base length is zero, the area of the window will be zero. There is also a limit on how large scan be: when x is large
enough, the rectangular portion of the window shrinks down to zero height. What is the exact largest value of r when this
occurs?
Largest x = ?
Answers
The base length that will maximize the area for such a window is 168.03 cm. The exact largest value of x when this occurs is 233.39 cm
Suppose we make an assumption that:
(x) should be the width of the rectangle base;(h) should be the height of the rectangleAlso, provided that the diameter of the semi-circle appears to be the base of the rectangle, then;
the radius \(\mathbf{r = \dfrac{x}{2}}\)and, the perimeter of the window can now be expressed as:
\(\mathbf{x + 2h + \pi r = x + 2h + \dfrac{\pi x }{2}}\)
\(\mathbf{= \Big ( 1 + \dfrac{\pi}{2}\Big) x + 2h}\)
Given that the perimeter = 600 cm
∴
\(\mathbf{ \Big ( 1 + \dfrac{\pi}{2}\Big) x + 2h= 600}\)
\(\mathbf{ h = 300 - \Big( \dfrac{1}{2} + \dfrac{\pi}{4}\Big) x}\)
Since h > 0, then:
\(\mathbf{ h = 300 - \Big( \dfrac{1}{2} + \dfrac{\pi}{4}\Big) x>0}\)
By rearrangement and using the inverse rule:
\(\mathbf{ x< \dfrac{ 300}{\Big( \dfrac{1}{2} + \dfrac{\pi}{4}\Big) } }\)
\(\mathbf{ x= \dfrac{ 1200}{\Big( 2 +\pi \Big) } }\)
\(\mathbf{ x= 233.39 \ cm }\)
Thus, the largest length x = 233.39 cm
However, the area of the window is given as:
\(\mathbf{A(x) = xh + \dfrac{1}{2} \pi r^2}\)
\(\mathbf{A = x \Big [ 300 - \Big ( \dfrac{1}{2}+\dfrac{1}{4} \Big) x \Big ] +\dfrac{1}{2}\pi \Big(\dfrac{x}{2} \Big )^2}\)
\(\mathbf{A (x) = 300x - \Big( \dfrac{1}{2} + \dfrac{\pi}{8}\Big) x^2 \ cm^2}\)
Now, at maximum, when the area A = 0. Taking the differentiation, we have:
\(\mathbf{\dfrac{d}{dx} 300x - \dfrac{d}{dx} \Big( \dfrac{1}{2} + \dfrac{\pi}{8}\Big) x^2 \ =0}\)
\(\mathbf{ 300 - 2x \Big( \dfrac{1}{2} + \dfrac{\pi}{8}\Big) \ =0}\)
Making x the subject of the formula, we have:
\(\mathbf{x = \dfrac{1200}{4 +\pi}}\)
x = 168.03 cm
Taking the second derivative:
\(\mathbf{\dfrac{d}{dx} \Big [300 -2x \Big( \dfrac{1}{2} + \dfrac{\pi}{8}\Big) \Big]}\)
\(\mathbf{= -2 \Big( \dfrac{1}{2}+\dfrac{\pi}{8}\Big ) <0}\)
Therefore, we can conclude that the maximum area that exists for such a window is 168.03 cm
Learn more about derivative here:
https://brainly.com/question/9964510?referrer=searchResults
A system of two linear equations is graphed on a coordinate plane. If the system of equations has infinitely many
solutions, which statement must be true?
A) On the graph, there are no points (z, y) that satisfy both equations.
B) On the graph, there is exactly one point (z,y) that satisfies both the equations.
C) On the graph, any point (z,y) that satisfies one of the equations cannot satisfy the other equation.
D) On the graph, any point (z,y) that satisfies one of the equations must also satisfy the other equation.