Kevin went shopping for a new scooter. He bought one on sale for 15% off its regular price of $140. If sales tax is 8%, what was the total cost of the scooter?
Answers
Answer:
128.52
Step-by-step explanation:
140 × (1-0.15) = 119
119 × 1.08 = 128.52
Answer:
$128.52
Step-by-step explanation:
Firstly to find the price of the scooter, you divide 140 by 100 and then multiply it by 15. The answer is what you subtract from the original price.
15(140/100) = 21
140 - 21 = 119
Now that we have the price of the scooter after the discount, we need to figure out the price of the sales tax. Sales tax is based on the reduced price, so we need to take the same steps as before to find the price. Divide 119 by 100, then multiply it by 8, then add the total to 119.
8(119/100) = 9.52
119 + 9.52 = 128.52
Answer = $128.52
Related Questions
an urn contains two red balls and three white balls. if a ball is chosen at random, what is the probability that it is white?
Answers
If an urn contains two red balls and three white balls and a ball is chosen at random, then the probability of getting white ball is 3/5
The number of red balls = 2 balls
The number of white balls = 3 balls
Total number of balls = 2 + 3
= 5 balls
The probability = Number of favorable outcomes / Total number of outcomes
Number of favorable outcomes = Number of white balls = 3
Total number of outcomes = 5
The probability = 3/5
Hence, if an urn contains two red balls and three white balls and a ball is chosen at random, then the probability of getting white is 3/5
Learn more about probability here
brainly.com/question/11234923
#SPJ4
VWXY is a parallelogram. Find the measure of XY and WY 8

Answers
Remember that
in a parallelogram, the diagonals bisect each other
that means
VZ=ZX
substitute given values
n+7=3n
solve for n
3n-n=7
2n=7
n=3.5
therefore
VX=(n+7)+3n ----> by addition segments postulate
VX=4n+7
substitute the value of n
VX=4(3.5)+7
VX=21Which trinomial did she factor?
x2 + 4x – 12
x2 + 2x - 6
x2 - 8x - 6
x2 - 4x - 12
Answers
Answer:
Answer is (D) x2 – 4x – 12
Step-by-step explanation:
edge 2020 test
7.) What is -10 has a fraction?
Answers
Nothing further can be done to this topic
In a class there are 11 boys and 19 girls.
The mean weight of all 30 children is 32.85 kg.
The mean weight of the 11 boys is 31.9 kg.
Work out the mean weight of the 19 girls.
Answers
Answer:
explain two ways in which the preservation of natural environments adds quality of life in a country : ,
Paula's Pizza Parlor uses the following ingredients to make pizza.
Number of Pizzas Sauce (oz) Cheese (oz)
2 18 12
5
At this rate, how much sauce and cheese will Paula use to make 5 pizzas?
Paula will use 30 oz of sauce and 45 oz of cheese to make 5 pizzas.
Paula will use 35 oz of sauce and 24 oz of cheese to make 5 pizzas.
Paula will use 45 oz of sauce and 30 oz of cheese to make 5 pizzas.
Paula will use 90 oz of sauce and 60 oz of cheese to make 5 pizzas.
Answers
Answer:
Paula will use 45 oz of sauce and 30 oz of cheese to make 5 pizzas
How to find quantity of ingredients for 5 pizzas?
To find this, you can use the proportion of ingredients used for 2 pizzas and scale it up to 5 pizzas.
For 2 pizzas, Paula uses 18 oz of sauce and 12 oz of cheese.
The proportion of sauce to cheese used is 18/12
To make 5 pizzas, you can use this proportion to find how much sauce and cheese is needed:
2 pizzas = 18 sauce
5 pizzas = 5 / 2 x 18 = 45 sauces.
For cheese required, Paula will use:
2 pizzas = 12 cheese
5 pizzas = 5 / 2 x 12 = 30 cheese.
So the total is 45 oz of sauce and 30 oz of cheese.
Learn more on pizza ingredients here: brainly.com/question/24659657
#SPJ1
Step-by-step explanation:
Answer:
Paula will use 45 oz of sauce and 30 oz of cheese to make 5 pizzas
Step-by-step explanation:
Factor the following binomials

Answers
solve initial value problem x2y'-xy=x2+4,
x>0, y(1)=0
Answers
The solution to the equation x²y' - xy = x² + 4, x > 0, y(1) is y = xln|x| - (2/x) +2
To find the solution, follow these steps:
The equation is of the form y'+Py = Q, where P= -1/x and Q= 1+ 4/x². So, we have to find the integrating factor: I.F. = \(e^{\int {P(x)} \, dx}\) where P(x) is the coefficient of y. So, ∫P(x)dx = -∫1/x dx = - ln |x|. Therefore, I.F. = \(e^{-ln|x|}\)= 1/x.The solution to the equation can be given as y × I.F= ∫I.F × Q(x) dx + C ⇒y × 1/x= ∫1/x +4/x³ dx + C ⇒ y/x= ln|x|- 2/x²∴ y = x*ln|x| - 2/x + C where C is the constant of integration.Since y(1) = 0, we can find the value of C⇒ 0 = 1 * ln(1) + 4/1 + C ∴ C = 2Therefore the required solution to the given differential equation is y = xln|x| - (2/x) +2Learn more about differential equation:
brainly.com/question/28099315
#SPJ11
Question 5 of 10
What is the solution to this equation?
6x + 10 - 2x = 7 + 23
A. X = 15
B. X= 4
C. X= 5
D. X= 2
Answers
Answer:
x=5
Step-by-step explanation:
First you combine the like terms. next you add 7+23. After that you subtract 10 from both sides. You're left with 4x=20. divide the equation by 4 on each term. Then you're left with x=5.
Start by isolating the constant from the variable values
6x-2x=7+23-10
4x=20
Then divide by 4
X=5
let sin(θ) =3/5 and tan(y) =12/5 both angels comes from 2 different right trianglesa)find the third side of the two tringles b) find sin (θ+y)
Answers
In a right triangle, we haev some trigonometric relationships between the sides and angles. Given an angle, the ratio between the opposite side to the angle by the hypotenuse is the sine of this angle, therefore, the following statement
\(\sin (\theta)=\frac{3}{5}\)Describes the following triangle
To find the missing length x, we could use the Pythagorean Theorem. The sum of the squares of the legs is equal to the square of the hypotenuse. From this, we have the following equation
\(x^2+3^2=5^2\)Solving for x, we have
\(\begin{gathered} x^2+3^2=5^2 \\ x^2+9=25 \\ x^2=25-9 \\ x^2=16 \\ x=\sqrt[]{16} \\ x=4 \end{gathered}\)The missing length of the first triangle is equal to 4.
For the other triangle, instead of a sine we have a tangent relation. Given an angle in a right triangle, its tanget is equal to the ratio between the opposite side and adjacent side.The following expression
\(\tan (y)=\frac{12}{5}\)Describes the following triangle
Using the Pythagorean Theorem again, we have
\(5^2+12^2=h^2\)Solving for h, we have
\(\begin{gathered} 5^2+12^2=h^2 \\ 25+144=h^2 \\ 169=h^2 \\ h=\sqrt[]{169} \\ h=13 \end{gathered}\)The missing side measure is equal to 13.
Now that we have all sides of both triangles, we can construct any trigonometric relation for those angles.
The sine is the ratio between the opposite side and the hypotenuse, and the cosine is the ratio between the adjacent side and the hypotenuse, therefore, we have the following relations for our angles
\(\begin{gathered} \sin (\theta)=\frac{3}{5} \\ \cos (\theta)=\frac{4}{5} \\ \sin (y)=\frac{12}{13} \\ \cos (y)=\frac{5}{13} \end{gathered}\)To calculate the sine and cosine of the sum
\(\begin{gathered} \sin (\theta+y) \\ \cos (\theta+y) \end{gathered}\)We can use the following identities
\(\begin{gathered} \sin (A+B)=\sin A\cos B+\cos A\sin B \\ \cos (A+B)=\cos A\cos B-\sin A\sin B \end{gathered}\)Using those identities in our problem, we're going to have
\(\begin{gathered} \sin (\theta+y)=\sin \theta\cos y+\cos \theta\sin y=\frac{3}{5}\cdot\frac{5}{13}+\frac{4}{5}\cdot\frac{12}{13}=\frac{63}{65} \\ \cos (\theta+y)=\cos \theta\cos y-\sin \theta\sin y=\frac{4}{5}\cdot\frac{5}{13}-\frac{3}{5}\cdot\frac{12}{13}=-\frac{16}{65} \end{gathered}\)

Problem 7. A car drives North for 1 km. Then it turns and drives 2 km at 30
∘
South of West. Finally the driver turns again and drives 0.5 km Northwest. (a) What is the total distance driven? (b) What are the magnitude and direction of the car's overall displacement? Problem 8. A circular track has a radius of 500 m. What is the displacement of a bicyclist when they travel around the track from the north side to the south side? When they make one complete circle around the track? Explain your answers.
Answers
In Problem 7, the total distance driven by the car is approximately 3.17 km. The car's overall displacement has a magnitude of approximately 1.84 km and is directed at an angle of approximately 45 degrees northwest.
In Problem 8, when a bicyclist travels around a circular track from the north side to the south side, their displacement is equal to the diameter of the track, which is 1000 m. When they make one complete circle around the track, their displacement is zero since they return to their starting point.
Problem 7:
To calculate the total distance driven, we sum up the distances traveled in each direction: 1 km + 2 km + 0.5 km = 3.5 km. So, the car has driven a total distance of approximately 3.17 km.
To find the car's overall displacement, we need to consider both the magnitude and direction. The first leg of the journey going north does not contribute to the displacement in the east-west direction. The second leg, driving 2 km at 30 degrees south of west, contributes to both the east and south directions. Using trigonometry, we can calculate the eastward component as 2 km * cos(30°) ≈ 1.73 km and the southward component as 2 km * sin(30°) ≈ 1 km. The third leg, driving 0.5 km northwest, contributes to both the east and north directions. Using trigonometry again, we can calculate the eastward component as 0.5 km * cos(45°) ≈ 0.35 km and the northward component as 0.5 km * sin(45°) ≈ 0.35 km. Adding up the eastward components (1.73 km + 0.35 km) and the northward components (1 km + 0.35 km), we find that the car's overall displacement has a magnitude of approximately 1.84 km and is directed at an angle of approximately 45 degrees northwest.
Problem 8:
When the bicyclist travels from the north side to the south side of the circular track, their displacement is equal to the diameter of the track. Since the track has a radius of 500 m, the diameter is 2 * 500 m = 1000 m. Therefore, the displacement when traveling from the north side to the south side is 1000 m.
When the bicyclist makes one complete circle around the track, they return to their starting point. Displacement is a vector that represents the change in position, and in this case, the change is zero since the starting and ending points coincide. Thus, the displacement when making one complete circle around the track is zero.
Learn more about angle here:
https://brainly.com/question/30147425
#SPJ11
does the 3-dimension flow given in cartesian coordinates here satisfy the incompressible continuity equation?
Answers
No, the 3-dimensional flow given in Cartesian coordinates does not satisfy the incompressible continuity equation.
The incompressible continuity equation is a fundamental equation in fluid dynamics that describes the conservation of mass. It states that the divergence of the velocity field should be equal to zero for an incompressible flow.
In Cartesian coordinates, the continuity equation can be written as:
∇ · V = ∂u/∂x + ∂v/∂y + ∂w/∂z = 0
where V = (u, v, w) represents the velocity field in the x, y, and z directions respectively.
To determine if the given 3-dimensional flow satisfies the incompressible continuity equation, we need to calculate the divergence of the velocity field and check if it equals zero.
Let's assume the velocity field is given as V = (x^2, y^2, z^2).
Calculating the divergence, we have:
∂u/∂x = 2x
∂v/∂y = 2y
∂w/∂z = 2z
∇ · V = ∂u/∂x + ∂v/∂y + ∂w/∂z = 2x + 2y + 2z
The divergence of the velocity field is equal to 2x + 2y + 2z, which is not equal to zero for all values of x, y, and z. Therefore, the given flow does not satisfy the incompressible continuity equation.
In an incompressible flow, the divergence of the velocity field should be zero at every point in the fluid domain, indicating that the flow is mass-conserving. However, in this case, the non-zero divergence suggests that the flow is compressible or that there is a change in density or mass within the fluid domain.
Visit here to learn more about divergence:
brainly.com/question/30726405
#SPJ11
write an equation in slope-intercept form for this line.

Answers
Answer:
y = \(\frac{3}{2}\) x - 1
Step-by-step explanation:
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
Here m = \(\frac{3}{2}\) , then
y = \(\frac{3}{2}\) x + c ← is the partial equation
To find c substitute (- 4, - 7 ) into the partial equation
- 7 = - 6 + c ⇒ c = - 7 + 6 = - 1
y = \(\frac{3}{2}\) x - 1 ← equation of line
Can someone please help me . WILL MARK BRAINLIEST !!!
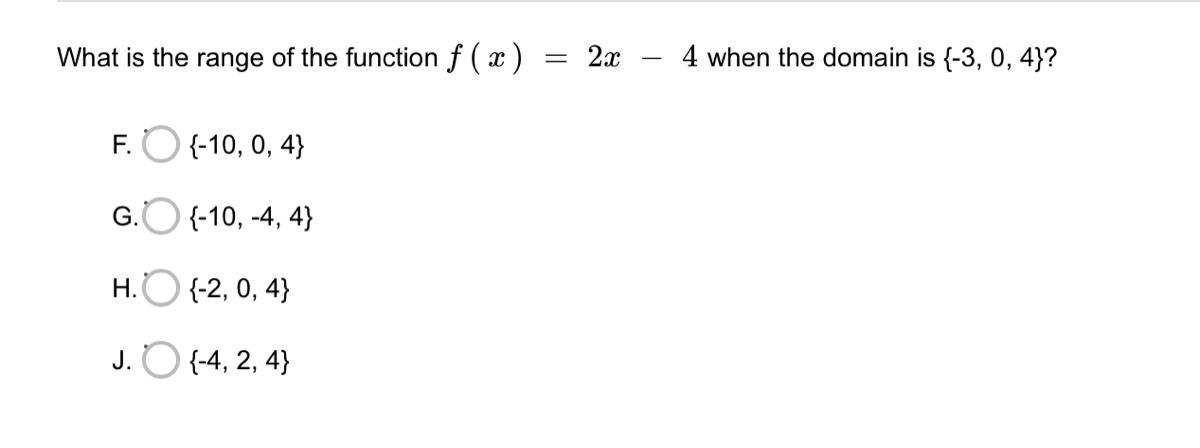
Answers
Answer:
The range is { -10,0,4}
Step-by-step explanation:
The domain is the input and the range is the output
f(-3) = 2(-3) -4 = -6-4 = -10
f(0) = 2(0) -4 = 0-4 = 0
f(4) = 2(4) -4 = 8-4 = 4
The outputs are { -10,0,4}
The range is { -10,0,4}
Answer:H
Step-by-step explanation:
You just take the domain, add 1 to the first number and the rest stay the same.
X-Y=4
-2X+6(4-X)=3
-8X+24=3
-24 -24
-8X=-21
X=21/8
Y=11/8
(21/8,11/8)
find the error in the problem.
Answers
Answer: You did wrong at Y=11/8! It should be -11/8, not positive 11/8
Step-by-step explanation:
You solved it all right; just the y is wrong! The reason why y is -11/8 is that a negative and a negative will make a positive, and add an x positive, and you will get a positive answer. If y is negative, the answer would be negative!
Slope is - 1/2 and (-3, 2) is on the line.
Answers
Answer:
y= -1/2x + 1/2
Step-by-step explanation:
First, use the point-slope formula: y-y1 = m(x-x1)
y-2 = -1/2(x-(-3))
y-2= -1/2x + -1.5
(subtract 2 from both sides)
y = -1/2x + 1/2
ALRIGHTY I NEED HELP AGAIN! YOU'LL GET BRAINLIEST IF YOU'RE CORRECT!

Answers
Step-by-step explanation:
third quadrant ( option C) is the correct answer.
hope this helps you.
Answer:it’s B cutie
Step-by-step explanation:
At the end of each month, Bill analyzes his extra expenses for the year. In April, he has 900 dollars
remaining in his account for extra expenses. He is spending 75 dollars each month. Write an equation in
point-slope form for Bill's finances. Let January be x= 1. Convert the equation into slope-intercept forn
Answers
Answer:
12
Step-by-step explanation:
900 divide by 75 = 12
The equation in slope-intercept form for Bill's finances is \(\(y = -75x + 975\).\) This equation represents the amount of money remaining in Bill's account for extra expenses at the end of each month.
Let's assume the number of months passed since January as "m" and the amount of money remaining in Bill's account for extra expenses at the end of each month as "y".
We are given the following information: In January (x = 1), Bill has not started spending yet, so he has all his expenses available. Therefore, at the beginning of January, he has $900 (y = 900) remaining for extra expenses.
Each month, Bill spends $75 on extra expenses. So, as the number of months increases, the remaining amount decreases.
Now, let's set up the equation in point-slope form using the point (1, 900) and the slope (-75): \(\[y - y_1 = m(x - x_1)\]\)
where:
\(\(y_1 = 900\) (remaining amount in January)\\\(m = -75\) (slope, indicating $75 reduction each month)\\\(x_1 = 1\) (January)\\\)
Now plug in the values: \(\[y - 900 = -75(x - 1)\]\)
Next, let's simplify the equation and convert it to slope-intercept form (y = mx + b) where "b" represents the y-intercept (the remaining amount when x = 0, i.e., the start of the year).
\(\[y - 900 = -75x + 75\]\)
To isolate "y," add 900 to both sides: \(\[y = -75x + 975\]\)
So, the equation in slope-intercept form for Bill's finances is \(\(y = -75x + 975\).\) This equation represents the amount of money remaining in Bill's account for extra expenses at the end of each month.
To know more about slope:
https://brainly.com/question/3605446
#SPJ3
ASAP WILL GIVE BRAINLIEST 73 POINTSS
Find the volume of the figure.
Volume =

Answers
Answer:
Solution given;
length[l]=20cm
for trapezoid
side 1=37cm
side 2=15cm
height[h]=25.7cm
we have
volume =area of trapezoid *length
=½*h(side 1+side2)*l=½*25.7(37+15)*2013364cm³the volume of the figure13364cm³.
Consider the following statement. The product of any even integer and any odd integer is even. (a) Suppose the given statement is rewritten in the form, v integers m and n, if (hypothesis] then [conclusion). Fill in the blanks to describe the hypothesis and The hypothesis is ( ---Select--- The conclusion is --Select-
Answers
The conclusion of the given statement is "The product of any even integer and any odd integer is even."
The hypothesis of the given statement is "If an integer is even and another integer is odd, then their product is even." The hypothesis represents the assumed condition that is required for the statement to be true. In this case, the hypothesis involves two integers, one even and one odd, and claims that their product will be even.
The conclusion is the statement that follows from the hypothesis. In this case, the conclusion is a generalization of the hypothesis, stating that the product of any even integer and any odd integer will always be even.
In symbolic form, the statement can be written as: For all even integers m and odd integers n, if m and n are multiplied, then the product mn is even. It is important to note that the given statement can be proven mathematically, using the properties of even and odd numbers. Specifically, an even number can be expressed as 2k, where k is an integer, and an odd number can be expressed as 2k+1. Thus, the product of an even and odd integer can be expressed as 2k(2k+1), which simplifies to \(4k^2\)+2k, an even integer. Therefore, the statement holds true.
Learn more about odd integer here:
https://brainly.com/question/490943
#SPJ11
Please help, this is called Writing Equations

Answers
Answer:
I think its the 2nd one im not sure tho
Step-by-step explanation:
Answer:
first one is 14.
second one is 131-11=6B
Step-by-step explanation:
1) 252/18=14
2) you want to know how much 6 books sre and it says you got 11 dollars change so u take 11 from 131 to get the price of 6 books
hope that helps :)
Don Miguel Hidalgo y costilla padre de la patria nació en hacienda de correr lejos no hay municipio de Pénjamo gto dio el grito de Dolores de la madrugada del 16 de septiembre de 1810 el 28 de septiembre de 1810 obtuvo su primer triunfo de tomar la Alhóndiga de Granaditas en la ciudad de Guanajuato murió fusilado el 30 de julio de 1211 en la ciudad de Chihuahua a la edad 5¿ en qué año nació el padre de la patria? Qué edad tenía Hidalgo cuando dio el grito de Dolores? Cuantos lustros completos? Cuantos lustros completoCuantos lustros completos vivió Hidalgo ?
Answers
Answer:
what I don't understand what you are saying
Answer for ten points!
Answers
Answer:
Step-by-step explanation:
The average score of students in the first group is 39, the second group is 32, and the third group is 43. If the numbers of students in the three groups are 24, 26, and 27, respectively, find the average score of all students.
Answers
The average score of all students, calculated by taking a weighted average based on the number of students in each group, is 38. The overall performance is slightly below the group averages.
The average score of students in the first, second, and third groups are 39, 32, and 43, respectively. There are 24 students in the first group, 26 students in the second group, and 27 students in the third group.
To find the average score of all students, we need to take a weighted average of the scores in each group, with the number of students in each group as the weights.
Here's how to do it: First, we calculate the total number of students:24 + 26 + 27 = 77. Then, we calculate the total score across all students: 39*24 + 32*26 + 43*27 = 936 + 832 + 1161 = 2929
Finally, we divide the total score by the total number of students to get the average score:2929/77 = 38. The average score of all students is 38.
This means that the overall performance of all the students is slightly below the average of the scores in each group.
For more questions on average score
https://brainly.com/question/13832161
#SPJ8
what is two ways to rewrite 21x^2 -42x +14 in equvalent form? i really need help here lol-
Answers
Answer:
7(3x^2-6x+2)
Step-by-step explanation:
21, 42, 14 they can be divided by 7 so we put 7 out
question 14 options: the mean number of visitors at a national park in one weekend is 52. assume the variable follows a poisson distribution. find the probability that there will be 58 visitors at this park in one weekend. (that is, find p(x
Answers
The probability that there will be 58 visitors at this park in one weekend is 0.0375.
The probability of a specific number of visitors (X) following a Poisson distribution is given by the equation:
P(X = k) = (e^(-λ) x λ^k) / k!
where λ is the mean number of visitors and k is the specific number of visitors.
Given that the mean number of visitors is 52, we can plug in the values to find the probability of 58 visitors:
P(X = 58) = (e^(-52) x 52^58) / 58!
P(X = 58) = 0.0374722
Using a calculator to compute the above expression, we get the probability of P(X = 58) = 0.0374722. Rounded to 4 decimal places, the answer is 0.0375.
The problem seems incomplete, it must have been...
"The mean number of visitors at a national park in one weekend is 52. Assume the variable follows a Poisson distribution. Find the probability that there will be 58 visitors in one weekend. That is, find P(X=58) Round to 4 decimal places. "
Learn more about Poisson distribution here: https://brainly.com/question/14802212
#SPJ4
Test the series for convergence or divergence.[infinity]∑ = (−1)^n−1.e^2/nn = 1
Answers
The given series is ∑ = (−1)n−1.e2/nn = 1. To test for convergence or divergence, we need to use the limit comparison test. This involves comparing the given series to a known convergent or divergent series. To use the limit comparison test, we need to find the limit of the ratio of the terms of the two series as n approaches infinity. In this case, the ratio of the two series is
limn→∞((-1)n−1·e2/nn ) / ((-1)n−1·1/n)
Simplifying this limit gives us
limn→∞(e2·n/nn+1)
This limit is equal to 0, so the ratio of the two series approaches 0. Since the known series, ∑ = (−1)n−1/n diverges, the given series must also diverge.
To summarize, the given series ∑ = (−1)n−1.e2/nn = 1 diverges according to the limit comparison test. This test was used by taking the limit of the ratio of the terms of the two series as n approaches infinity. The limit of the ratio of the two series was 0, so the given series diverges like the known series.
To know more about convergence or divergence refer here:
https://brainly.com/question/15415793
#SPJ11
Let x = 3, y = -2, and z = 5, Evaluate 8x2 -6y + 2z
Answers
(I have to use up room or else I can’t submit)

Please help‼️ domain and range‼️

Answers
The domain and the range of the function are (-∝, ∝) and (0, ∝), respectively
Calculating the domain and range of the graph?From the question, we have the following parameters that can be used in our computation:
The graph
The above graph is an exponential function
The rule of an function is that
The domain is the set of all real values
In this case, the domain is (-∝, ∝)
For the range, we have
Range = (0, ∝)
Read more about domain and range at
brainly.com/question/27910766
#SPJ1
A spring with spring constant 0.5 m has a force of 40 newtons applied to it. How much does the spring
stretch? Use Hooke's law F = kx
N
O A 1,600 cm
OB. 100 cm
O C. 80 cm
O D. 40 cm
Answers
The spring stretch by 80cm if a spring constant 0.5 m has a force of 40 newtons applied to it
How to calculate the force acting on string?According to Hookes law
F = ke
where
F is the applied force = 40N
k is the spring constant
e is the extension = 0.5
Substitute
40 = 0.5e
e = 40/0.5
e = 80cm
Hence the spring stretch by 80cm if a spring constant 0.5 m has a force of 40 newtons applied to it
Learn more on hookes law here: https://brainly.com/question/12253978