Katie has a doll house that is a small model of a real Victorian house. The real house has a rectangular window that measures 65 centimeters long by 45 centimeters wide. The length of the window in Katie's house is 13 centimeters long. How wide is the window in Katie's house?
Answers
Answer:
9
Step-by-step explanation:
65/13=5
45/5=9 The answer is 9
Related Questions
how do you calculate monthly forecasting 3 month moving
average
Answers
To calculate a three-month moving average for monthly forecasting, you need to follow these steps: Gather the historical data, Determine the time period, Calculate the moving average, Repeat the process.
Gather the historical data: Collect the monthly data for the specific variable you want to forecast. For example, if you want to forecast sales, gather the sales data for the past several months.
Determine the time period: Decide on the time period for your moving average. In this case, it is three months.
Calculate the moving average: Add up the values for the variable you are analyzing over the past three months and divide the sum by three to get the average. This will be your moving average value for the third month.
Repeat the process: Shift the time period by one month and calculate the moving average for the new three-month period. Continue this process for each subsequent month, updating the time period and calculating the moving average accordingly.
For example, let's say you have the following sales data for the past six months:
Month 1: 100 units
Month 2: 120 units
Month 3: 110 units
Month 4: 130 units
Month 5: 140 units
Month 6: 150 units
To calculate the three-month moving average for Month 4, you would add up the sales values for Month 2, Month 3, and Month 4 (120 + 110 + 130 = 360) and divide it by three to get an average of 120 units. Repeat this process for each subsequent month to obtain the moving average values for your forecast.
Note that the number of data points you include in the moving average calculation and the frequency of the data (monthly in this case) can be adjusted based on your specific needs and the nature of the data.
Learn more about data from
https://brainly.com/question/30459199
#SPJ11
How much metal is needed to cast a cubical metal box?
Answers
Depending on the size and thickness of the box, a certain amount of metal is required to cast a cubical metal box.
Depending on the size and thickness of the box, a certain amount of metal is required to cast a cubical metal box. In general, more metal is required for larger, thicker boxes. One must first calculate the box's volume in order to determine how much metal is required. The box's length, width, and height can be multiplied together to get this. The thickness of the metal must next be determined. The total amount of metal required can be estimated by multiplying the volume of the box by the thickness of the metal once the volume and thickness of the metal have been established. For instance, consider a box with dimensions of 6 inches long, 6 inches wide, and 6 inches high and a metal thickness.
Learn more about amount here
https://brainly.com/question/28970975
#SPJ4
Please Help! 60 points for a rapid reply- please look at the question below= The Figure of circle A shown has a diameter of PR which intersects with QS at point B and the measurements shown, Calculate the following measures-


Answers
The measure of the angles of the cyclic quadrilateral are:
Arc PQ = 130
QR = 50°
Arc RS = 70°
∠PSQ = 65°
∠PSB = 65°
∠SBP = 80°
AQS = 30°
PS = 110°
How to find the angles and lengths in cyclic geometry?From the figure, the arc PQ is subtended by the angle PAQ.
This means that:
PQ = ∠PAQ
Given that ∠PAQ = 130, it means that:
Arc PQ = 130
The measure of PSQ is then calculated using:
∠PSQ = 0.5 * Arc PQ ----- inscribed angle is half a subtended angle.
This gives: ∠PSQ = 0.5 * 130
∠PSQ = 65°
Hence, the measure of ∠PSQ is 65°
The measure of arc QR
A semicircle measures 180°
Thus:
QR + PQ = 180°
Thus, we get:
QR = 180° - PQ
Substitute 130° for PQ
QR = 180° - 130°
QR = 50°
Hence, the measure of QR is 50°
The measure of arc RS
The measure of arc RS is then calculated using:
∠RPS = 0.5 * Arc RS ----- inscribed angle is half a subtended angle.
Where ∠RPS = 35
So, we have:
35 = 0.5 * Arc RS
Multiply both sides by 2
Arc RS = 70°
The measure of angle AQS
In (a), we have:
∠PSQ = 65°
This means that:
∠PSQ = ∠PSB = 65°
So, we have:
∠PSB = 65°
Next, calculate SBP using:
∠SBP + ∠BPS + ∠PSB = 180° ---- sum of angles in a triangle.
So, we have:
∠SBP + 35 + 65 = 180°
∠SBP + 100 = 180
∠SBP = 80°
The measure of AQS is then calculated using:
AQS = AQB = 180 - (180 - SBP) - (180 - PAQ)
AQS = 180 - (180 - 80) - (180 - 130)
AQS = 30°
The measure of arc PS
A semicircle measures 180°
This means that:
PS + RS = 180°
This gives
PS = 180 - RS
RS = 70
Thus:
PS = 180 - 70
PS = 110°
Read more about Cyclic geometry at: https://brainly.com/question/27884509
#SPJ1
there are 300 students in the 6th grade class, 4 are running for class president. which type of survey below would give valid results?
a. survey three 6th graders
b. survey six 6th graders
c. survey ten 6th graders
d. survey thirty 6th graders
Answers
step by step
A large hotel has 444 rooms. There are 5 floors, and each
floor has about the same number of rooms. Which number
is a reasonable estimate of the number of rooms on a floor? ANSWER FASTTT
Answers
Answer:
88 rooms
Step-by-step explanation:
444 / 5 = 88.8
Financial mathematics (see picture)

Answers
Answer:
i think it's the answer in the pic I have send you okk see and mark me brainliest answer okk thanks

A poster whose area is 180 square inches, has 1 inch margin at bottom and on sides 2 inch margin at the top. What are its dimensions for which printed area is maximized?
Answers
The dimensions for which the printed area is maximized are 16.432 × 10.954 in².
let the height of the poster = x inches
area of the poster = 180 in²
thus, its width is 180/x inches.
The printed area has a height of x - 3 inches due to the 1-inch bottom margin and 2-inch top margin.
The sides have a margin of 1 inch, so the width of the printed area is:
180/x - 2
the area of printed area A is given by the formula of a rectangle,
A = height × width
A = (x-3)(180/x - 2)
A = 180 - 2x - 540/x + 6
the maximized area is when dA/dx = 0
dA/dx = - 2 - 540(- 1/x²) = 0
540/x² = 2
x = √270
hence height = √270 = 16.432 inches,
and width = 180/√270 = 10.954 inches.
know more about the maximized area here: https://brainly.com/question/28821169
#SPJ4
3.5+y=-1 solve for y
Answers
Answer:
C is your best bet i got it good on ed
Answer:
-4.5
Step-by-step explanation:
The legs of a right triangle measure 18 cm and 26 cm.
What is the length of the hypotenuse?
Enter your answer, in simplest radical form, in the box.
Answers
Answer: The length of the hypotenuse of the right-angled triangle is 31.62 cm.
Step-by-step explanation: Given , that the legs of the right-angled triangle are 18 cm and 26 cm
Lets assume that the two sides of the right-angled triangle :
AC = 18 cm , BC = 26 cm
According to Pythagoras Theorem - In a right- angled triangle , the square of the hypotenuse side is equal to the sum of squares of two sides .
Therefore, according to the diagram AB² = AC² + BC²
⇒ AB² = (18)² + (26)²
⇒ AB² = 324 +676
⇒ AB² = 1000
⇒ AB = √1000
⇒ AB = 31.62 cm
Read more about Pythagoras Theorem: https://brainly.in/textbook-solutions/q-state-pythagoras-theorem-converse-1?source=qa-qp-match

Flag
Let A, B, and C be non-singular 2x2 matrices, I the 2x2 identity matrix and k a scalar. The following statements are incorrect. For each statement, write down the correct version of the right hand side.
(a) (A+B)2 = A2+2AB+B2
(b) (A-kI)3 = A3-3kA2+3k2A-k3
(c) CA=B C=B/A
Please show logical and detailed work.
Answers
Answer:
Step-by-step explanation:
(a)
\((A+B)^2=A^2+AB+BA+B^2\\\)
(b)
\((A-kI)^3=A^3-3kA^2+3k^2A-k^3I\)
(c)
\(CA=B\ \Longrightarrow\ C=B*A^{-1}\)
What is 7! Like seven times all the numbers below it
Answers
This problem is about graphs. In each of the following cases, either draw a graph with the stated property, or prove that no such graph exists. (For the purpose of this problem, a "graph" must have no loops or multiple edges.) (a) A graph on 16 vertices in which every vertex has degree 4. (b) A graph on 15 vertices in which 8 vertices have degree 6 and 7 vertices have degree 5 . (c) A graph on 14 vertices in which every vertex has degree 3 and the shortest cycle has length 6. (The second condition means that there is at least one cycle of length 6 , and no cycles of any length shorter than 6.) (d) A graph on 11 vertices in which every vertex has degree at least 6 and there are no cycles of length 3 .
Answers
(a) Consider a regular graph, such as a regular 4-regular graph or a 4-cube. (b) It is not possible to have a graph with the given conditions.(c) It is not possible to have a graph with the given conditions. (d) Such a graph is possible.
(a) To have a graph with 16 vertices where every vertex has degree 4, we would need a total degree of 4 * 16 = 64. However, the total degree must be even since each edge contributes 2 to the total degree. But 64 is an even number, which means such a graph is possible. One way to construct such a graph is to consider a regular graph, such as a regular 4-regular graph or a 4-cube.
(b) In a graph with 15 vertices, if 8 vertices have degree 6, then the total degree would be 8 * 6 = 48. Similarly, if 7 vertices have degree 5, the total degree would be 7 * 5 = 35. However, the total degree must be even, and 48 and 35 are both odd numbers. Therefore, it is not possible to have a graph with the given conditions.
(c) If we have a graph on 14 vertices where every vertex has degree 3 and the shortest cycle has length 6, it implies that there are cycles of length 6 but no cycles of length less than 6. This contradicts the fact that if there is a cycle of length 6, there will also be cycles of length less than 6 (such as 3, 4, and 5). Therefore, it is not possible to have a graph with the given conditions.
(d) To have a graph on 11 vertices where every vertex has a degree of at least 6 and there are no cycles of length 3, we can consider a complete bipartite graph K(6, 5). This graph has 6 vertices of degree 6 and 5 vertices of degree 5. It satisfies the given conditions because every vertex has a degree of at least 6, and there are no cycles of length 3 since it is bipartite. Thus, such a graph is possible.
Learn more about graph from below link
https://brainly.com/question/19040584
#SPJ11
Identify the vertex of the following parabola.
y = x2 - 4x +1
Answers
Answer:
Step-by-step explanation:
Image result for Identify the vertex of the following parabola. y = x2 - 4x +1
To find the vertex of a parabola, you first need to find x (or y, if your parabola is sideways) through the formula for the axis of symmetry. Then, you'll use that value to solve for y (or x if your parabola opens to the side) by using the quadratic equation. Those two coordinates are your parabola's vertex.
Any help please? Don’t understand

Answers
robin is twice as old as earl and adam is 8 years younger than earl. in 6 years robin will be three times as old as adam. find their present ages
Answers
The present age of Earl is 12 years, Robin is 24 years and Adam is 4 years old.
Let us consider the present age of Earl to be x years.
According to the given question, the present age of Robin is twice that of Earl = 2x
And since it is given that Adam is 8 years younger than Earl, then his age
= x - 8
After 6 years, the age of Earl will be x + 6
Robin's age will be = 2x + 6
Adam's age will be = x - 8 + 6 = x - 2
According to the given question, Robin's age will be thrice the age of Adam.
Hence, 2x + 6 = 3 (x - 2)
⇒ 2x + 6 = 3x - 6 ⇒ 6 + 6 = 3x - 2x ⇒ 12 = x
Thus, the present age of Earl is 12 years,
Robin's age = 2x = 2 x 12 = 24 years
Adam's age = x - 8 = 12 - 8 = 4 years
To know more about age problems:
https://brainly.com/question/29283654
#SPJ4
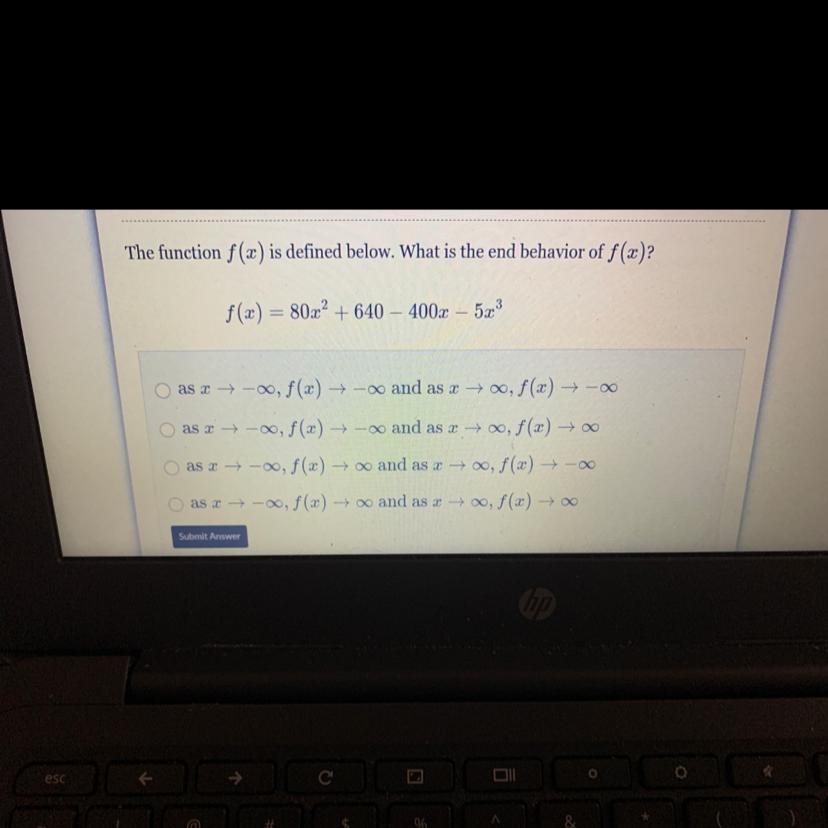
The function f(x) is defined below. What is the end behavior of f(x)?
f(x) = 80x* 2 + 640 - 400х - 52
Answers
The end behavior will be as x approaches infinity, and negative infinity, f(x) approaches infinity.
What is a function?Function is a type of relation, or rule, that maps one input to specific single output.
The function f(x) is defined as:
→ f(x)= 80x* 2 + 640 - 400x - 52
We need the degree and the leading coefficient to determine the behavior.
Since our leading coefficients has a leading even degree of 5, and a positive number,
The function will Rises to the left and falls to the right.
The end behavior will be as x approaches infinity, and negative infinity, f(x) approaches infinity.
Learn more about function here:
brainly.com/question/2253924
#SPJ2
Select the correct answer. Let f(x) and g(x) be polynomials as shown below. Which of the following is true about f(x) and g(x)? f(x) and g(x) are closed under multiplication because when multiplied, the result will be a polynomial. f(x) and g(x) are closed under multiplication because when multiplied, the result will not be a polynomial. f(x) and g(x) are not closed under multiplication because when multiplied, the result will be a polynomial. f(x) and g(x) are not closed under multiplication because when multiplied, the result will not be a polynomial.
Answers
f(x) and g(x) are not closed under subtraction because when subtracted, the result will be a polynomial, the correct option is B.
What is Polynomial?A polynomial is a mathematical equation that solely uses the operations addition, subtraction, multiplication, and non-negative integer exponentiation of variables. Variables are sometimes known as indeterminate in mathematics. Majorly used polynomials are binomial and trinomial.
Given f(x) and g(x) two polynomial functions in the standard form of the polynomial,
According to Closure Property, when something is closed, the output will be the same as the input.
The polynomials f(x) and g(x) can be seen in the image.
On subtracting the two polynomials, the output will be a polynomial and so it is closed under subtraction.
Therefore, The reason why f(x) and g(x) are not closed under subtraction is that the outcome of subtraction will be a polynomial, making option B the best choice.
Learn more about Polynomials here:
https://brainly.com/question/11536910
#SPJ1
Complete question:

What is the perimeter of this figure?3x - 1x2-3xPerimeter3x² - 11xx+22+

Answers
Given:
Width of the building = 2y
Length of the building = 9y-4
Find-:
Area of building in terms of y.
Explanation-:
The area of a rectangle is:
\(A=\text{ Length}\times\text{ Width}\)So the area of the given building is:
\(A=2y\times(9y-4)\)Area is:
\(\begin{gathered} A=2y\times(9y-4) \\ \\ =2y(9y)-4(2y) \\ \\ =18y^2-8y \end{gathered}\)The expression of area is:
\(18y^2-8y\)a set of exam scores is normally distributed and has a mean of 77.4 and a standard deviation of 7.8. what is the probability that a randomly selected score will be between 77 and 83?
Answers
The probability that a randomly selected score will be between 77 and 83 is 0.2841
The probability that a randomly selected score will be between 77 and 83 can be found using the Z-score formula and the standard normal distribution table.
First, we need to calculate the Z-scores for both 77 and 83 using the formula:
Z = (X - μ)/σ
Where X is the score, μ is the mean, and σ is the standard deviation.
For 77:
Z = (77 - 77.4)/7.8 = -0.05
For 83:
Z = (83 - 77.4)/7.8 = 0.72
Now, we can use the standard normal distribution table to find the probability for each Z-score. The table gives us the area to the left of the Z-score on the standard normal distribution curve.
For Z = -0.05, the probability is 0.4801.
For Z = 0.72, the probability is 0.7642.
To find the probability that a randomly selected score will be between 77 and 83, we need to subtract the smaller probability from the larger probability:
0.7642 - 0.4801 = 0.2841
Therefore, the probability that a randomly selected score will be between 77 and 83 is 0.2841.
To know more about Z-score click on below link:
https://brainly.com/question/30557336#
#SPJ11
7.) There were thirty-eight bales of hay in the barn. Dylan stacked more bales in the barn
today. There are now ninety-nine bales of hay in the barn. How many bales did he store in the
barn?
Answers
Answer:
61 bales of hay
Step-by-step explanation:
38 + 61 = 99
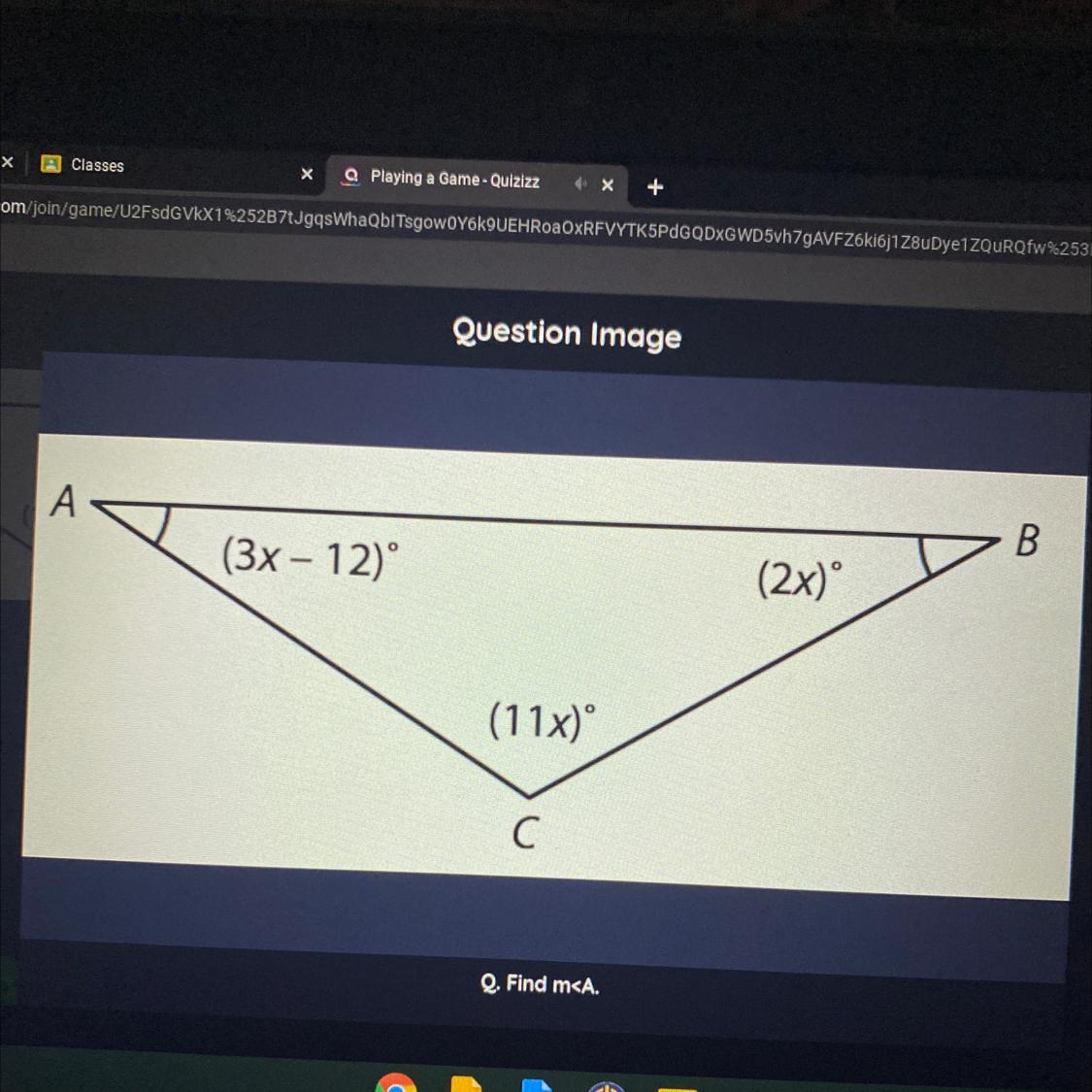
Find m
A 36
B 132
C 24
D 12
Answers
Answer:
12
Step-by-step explanation:
sum of all angles of triangle =180
3x-12+2x+11x=180
16x-12=180
16x=192
x=12
___________
\( \: \)
\(\boxed{ \rm{answer \: by \: { \boxed{ \rm{☆HayabusaBrainly}}}}}\)
3x - 12 + 2x + 11x = 180°
16x - 12 = 180°
16x = 180 + 12
16x = 192
x = 192 ÷ 16
x = 12✔ (D.)
Find the distance between the two endpoints.
(-6, 1) and (-3, 1)
Answers
Answer:
3
Step-by-step explanation:
distance formula
It takes a word processor 33 minutes to word process and spell check 6 pages. Find how long it takes her to word process and spell check 26 pages.
Answers
Answer:
it would take them 143 minutes
Answer two questions about Equations A and B:
A. 3x– 1=7
B. 3x = 8
1) How can we get Equation B from Equation A?
Answers
An equation is formed of two equal expressions. We can get Equation B from Equation A by adding 1 to both the sides of equation A, while the solution of both the equations is 8/3.
What is an equation?An equation is formed when two equal expressions are equated together with the help of an equal sign '='.
1.) The given equation A can be solved as shown below,
3x – 1 = 7
Add 1 to both the sides of the equation,
3x – 1 + 1 = 7 + 1
3x = 8 {∴ Equation B}
Divide both the sides of the equation by 3,
3x/3 = 8/3
x = 8/3
Thus, the solution of the equation is x=8/3.
2.) We can get Equation B from Equation A by adding 1 to both the sides of equation A, while the solution of both the equations is 8/3.
Learn more about Equation here:
https://brainly.com/question/14686792
#SPJ2
Emma is scrapbooking. She has 9 inches of paper and needs to cut it into 2/5 inch strips of paper. How many whole strips will she be able to make?
*
1 point
Answers
The number of strips Emma will be able to make 22.5 i.e. 22.
What is strips?The set of points in the plane between two parallel lines in the plane. The x,y coordinates plane of the points in the stripe satisfy the inequality C1 < . Ax + By < C2, where A, B, C1, C2 are certain constants and both A and B cannot be zero. The strip number is typically used in preparing the data for matching (or as a matching transformation within the matching processor). For text data that has numbers in the data but that you know are irrelevant, removing the numbers before matching is useful. As an abstract topological space, the Mobius strip can be embedded in three-dimensional Euclidean space in various ways. The twist is greater than 1 or the centerline is knotted.According to question
Total paper = Total strips × size of one
9 = n × 2/5
n = 22.5
To learn more about strips from the given link :
https://brainly.com/question/12142819
#SPJ1
Do the following summarize a categorical variable or a numerical variable? If the data is numerical, also state if it is continuous or discrete. Explain.
For a baseball player, his batting average during the playoffs.
Answers
The batting average of a baseball player is classified as a numeric continuous variable.
What are categorical and numerical variables?Categorical variables assume labels, for example, good or bad.Numerical variables assume numbers, as it own name says.A batting average is given by the number of hits divided by the number of at bats, hence it is a numeric value.
What are continuous and discrete variables?Continuous variables assume real values.Discrete variables assume integer values.The batting average is a real number, hence it is also a continuous variable.
More can be learned about classification of variables at https://brainly.com/question/17226865
#SPJ1
Barbara, a school superintendent, asks the local school board for permission to hire an additional teacher whenever the student enrollment at a certain grade level within a school increases by 35 students beyond capacity. This is an example of which type of decision
Answers
Answer:
Programmed
Step-by-step explanation:
Programmed Decisons may be classified as those actions which are routinely carried out or performed based on existing rules and protocol. In programmed decision making, the rules are in place, therefore once the criteria or requirement for which the rule or routine is to be enforced arises, programmed Decisons are made. In the scenario, the superintendent required that a programmed Decison be made in cases or situations where enrollment increases by 35 student beyond capacity, Hence, with this, every time this occurs the additional teachers will be hired.
Consider the array A=⟨30,10,15,9,7,50,8,22,5,3⟩. 1) (5 points) write A after calling the function BUILDMAX-HEAP(A) 2) (5 points) write A after calling the function HEAPINCREASE-KEY(A,9,55). 3) (5 points) write A after calling the function HEAPEXTRACT-MAX(A) Part 2) uses the array A resulted from part 1). Part 3) uses the array A resulted from part 2). * Note that HEAP-INCREASE-KEY and HEAP-EXTRACT- MAX operations are implemented in the Priority Queue lecture.
Answers
A after calling the function BUILDMAX-HEAP A=⟨50, 22, 30, 10, 7, 15, 8, 9, 5, 3⟩, A after calling the function HEAPINCREASE-KEY A=⟨55, 22, 30, 10, 7, 15, 8, 9, 55, 3⟩ and A after calling the function HEAPEXTRACT-MAX(A) max=55, uses the array A resulted from part 1 A=⟨30, 22, 15, 10, 7, 3, 8, 9⟩.
Given, the array A=⟨30,10,15,9,7,50,8,22,5,3⟩
1. BUILDMAX-HEAP(A) builds the max-heap from array A. It is given by:```
BUILDMAX-HEAP(A)
1 heap-size[A] ← length[A]
2 for i ← ⌊length[A]/2⌋ downto 1
3 do MAX-HEAPIFY(A, i)
```Step 1: Calculate the floor value of length of A/2 = 5.
Step 2: Build a Max-Heap with the following values, the heap at each step is shown below.
i=5:MAX-HEAPIFY(A, 5).
A=⟨30, 10, 15, 9, 7, 50, 8, 22, 5, 3⟩.
i=4: MAX-HEAPIFY(A, 4).
A=⟨30, 10, 15, 22, 7, 50, 8, 9, 5, 3⟩.
i=3: MAX-HEAPIFY(A, 3).
A=⟨30, 10, 50, 22, 7, 15, 8, 9, 5, 3⟩.
i=2: MAX-HEAPIFY(A, 2).
A=⟨30, 22, 50, 10, 7, 15, 8, 9, 5, 3⟩.
i=1: MAX-HEAPIFY(A, 1).
A=⟨50, 22, 30, 10, 7, 15, 8, 9, 5, 3⟩.
2. HEAPINCREASE-KEY(A,9,55) increases the value of the key at index 9 from 3 to 55, and restores the max-heap property by traversing the tree upwards.
It is given by:```HEAP-INCREASE-KEY(A, i, key)
1 if key < A[i]
2 then error “new key is smaller than current key”
3 A[i] ← key
4 while i > 1 and A[PARENT(i)] < A[i]
5 do exchange A[i] ↔ A[PARENT(i)]
6 i ← PARENT(i)```Step 1: Change the key value of A[9] to 55. A=⟨50, 22, 30, 10, 7, 15, 8, 9, 55, 3⟩.
Step 2: Traverse upwards to restore the Max-Heap property, A=⟨50, 22, 55, 10, 7, 30, 8, 9, 15, 3⟩.
3. HEAPEXTRACT-MAX(A) extracts the maximum element from the max-heap A and restores the max-heap property after extraction.
It is given by:```HEAP-EXTRACT-MAX(A)
1 if heap-size[A] < 1
2 then error “heap underflow”
3 max ← A[1]
4 A[1] ← A[heap-size[A]]
5 heap-size[A] ← heap-size[A] - 1
6 MAX-HEAPIFY(A, 1)
7 return max```Step 1: Extract the maximum element and swap it with the last element. A=⟨15, 22, 55, 10, 7, 30, 8, 9, 3⟩.Step 2: Restore the Max-Heap property, A=⟨55, 22, 30, 10, 7, 15, 8, 9, 3⟩.
Therefore, the answers are:
1. A=⟨50, 22, 30, 10, 7, 15, 8, 9, 5, 3⟩
2. A=⟨55, 22, 30, 10, 7, 15, 8, 9, 55, 3⟩
3. max=55, A=⟨30, 22, 15, 10, 7, 3, 8, 9⟩.
Learn more about array from the given link;
https://brainly.com/question/28061186
#SPJ11
Find the sum of each series. Σ¹° n=4 (0.8 n-0.4)
Answers
The given series is an arithmetic series and its sum is 36.4
The summation or sigma notation is used to express long summation into a single formula.
The series, given in a summation notation, is:
\(\sum\limits^{10}_{n=4} {(0.8n-0.4)}\)
The formula inside the sum notation represent the nth term, a(n).
Let evaluate the terms for some n, starts from n = 4 as indicated by the lower limit of the summation notation:
a(4) = 0.8 (4) - 0.4 = 2.8
a(5) = 0.8 (5) - 0.4 = 3.6
a(6) = 0.8 (6) - 0.4 = 4.4
This form a new arithmetic series, with the first term, let say f(1) =2.8 and common difference, d = 0.8.
The number of terms in this new geometric series is given by the upper and lower limit of the summation notation:
number of terms = 10 - 4 + 1 = 7
Use the sum formula for an arithmetic series,
S(n) = n/2 [2.f(1) + (n - 1) . d]
Substitute n = 7, f(1) = 2.8, and d = 0.8 into the formula:
S(7) = 7/2 [2. (2.8) + (7 - 1) . (0.8)]
S(7) = 36.4
Learn more about series here:
https://brainly.com/question/18304639
#SPJ4
what is the minimum number of coin tosses do you have to have have such that the odds of getting a heads is more than 50%
Answers
The minimum number of coin tosses required to have more than a 50% chance of getting at least one head is two.
How do we calculate?The possible outcomes of flipping a coin:
Heads (H)Tails (T)If the coin is flipped more than once, there are only two possible outcomes: H or T, whereby each outcome has a 50% chance of occurring.
So let us say that the coin is flipped twice, we have four possible outcomes:
HH, HT, TH, and TT.In this case, the only outcome that do not have at least one head is TT.
In conclusion, the probability of getting at least one head is 1 - (1/2 x 1/2) = 3/4, or 75% which is greater than 50%
Learn more about probability at:
https://brainly.com/question/24756209
#SPJ1