John went deep sea diving with some friends. If he descends (goes down) at a rate of 3
feet per minute, what is John’s depth in 50 minutes?
Answers
150
Yeah that it’s
Related Questions
whitch is greater 2 yards or 5 feet
Answers
Answer:
Two yards
Step-by-step explanation:
2 yards = 6 feet
*SOCIAL DISTANCE RULES APPLY IN YOUR STATE*
Answer:
2 yards
Step-by-step explanation:
Yes 1 yard equals 3 feet so 2 yards is 6 feet making 2 yards greater than 5 feet
Find the generating function of the sequence {an}n≥0 determined by an = an−1 + 6an−1 with initial conditions a0 = 1, a1 = 3. You need to find the closed form of the generating function, but you don’t need find the closed form of the coefficients.
Answers
The generating function for the sequence {an} is given by a(x) = (1 + 2x) / (1 - x - 6x^2). It captures the terms of the sequence {an} as coefficients of the powers of x.
To find the generating function of the sequence {an}, we can use the properties of generating functions and solve the given recurrence relation.
The given recurrence relation is: an = an-1 + 6an-2
We are also given the initial conditions: a0 = 1 and a1 = 3.
To find the generating function, we define the generating function A(x) as:
a(x) = a0 + a1x + a2x² + a3x³ + ...
Multiplying the recurrence relation by x^n and summing over all values of n, we get:
∑(an × xⁿ) = ∑(an-1 × xⁿ) + 6∑(an-2 × xⁿ)
Now, let's express each summation in terms of the generating function a(x):
a(x) - a0 - a1x = x(A(x) - a0) + 6x²ᵃ⁽ˣ⁾
Simplifying and rearranging the terms, we have:
a(x)(1 - x - 6x²) = a0 + (a1 - a0)x
Using the given initial conditions, we have:
a(x)(1 - x - 6x²) = 1 + 2x
Now, we can solve for A(x) by dividing both sides by (1 - x - 6x^2²):
a(x) = (1 + 2x) / (1 - x - 6x²)
Therefore, the generating function for the given sequence is a(x) = (1 + 2x) / (1 - x - 6x²).
Read more on Functions here: https://brainly.com/question/29890699
#SPJ11
Problem 4. Write a formula for the solution of 1D heat equation (a) {
u
t
+2u=16u
xx
+x,x∈R,t>0
u(x,0)=e
−x
2
,x∈R.
(b) {
u
t
−3u=u
xx
+1,x∈R,t>0
u(x,0)=
x
2
+1
1
,x>0
Answers
The general solution to the 1D heat equation with the given initial condition is:u(x, t) = (A*e^(√(λ^2 + 3)x) + B*e^(-√(λ^2 + 3)x)) * e^(λ^2 + 3)t.
(a) The 1D heat equation with the given initial condition can be solved using the method of separation of variables. Let's denote the solution as u(x, t).
Assuming the solution can be expressed as a product of two functions: u(x, t) = X(x) * T(t), we can substitute this into the heat equation:
T' * X + 2 * T * X'' = 16 * X'' * T + X.
Dividing both sides by u(x, t) = X(x) * T(t), we get:
(T' / T) + 2 * (X'' / X) = 16 * (X'' / X) + 1 / T.
Since the left side depends only on t and the right side depends only on x, they must be equal to a constant value, denoted as -λ^2.
So, we have two separate ordinary differential equations:
T' / T = -λ^2 - 2,
X'' / X = -λ^2 / 16.
Solving the first equation for T(t), we get:
T(t) = Ce^(-λ^2 - 2)t.
Solving the second equation for X(x), we get:
X'' - (-λ^2 / 16)X = 0.
This is a homogeneous second-order linear differential equation with characteristic equation:
r^2 + (λ^2 / 16) = 0.
Solving this characteristic equation, we find two solutions:
r = ±(iλ / 4).
The general solution for X(x) can be written as:
X(x) = A*cos(λx / 4) + B*sin(λx / 4).
Combining the solutions for T(t) and X(x), we have:
u(x, t) = (A*cos(λx / 4) + B*sin(λx / 4)) * Ce^(-λ^2 - 2)t.
Now, we need to apply the initial condition u(x, 0) = e^(-x^2). Plugging in the values, we get:
e^(-x^2) = (A*cos(λx / 4) + B*sin(λx / 4)) * Ce^(-λ^2 - 2) * 0.
Since the initial condition holds for all x, we can ignore the x terms. This leads to:
e^(-x^2) = Ce^(-λ^2 - 2) * 0.
From this, we obtain C = e^(-x^2) for any λ.
Therefore, the general solution to the 1D heat equation with the given initial condition is:
u(x, t) = (A*cos(λx / 4) + B*sin(λx / 4)) * e^(-λ^2 - 2)t.
(b) Similarly, we can solve the 1D heat equation with the given initial condition:
Assuming u(x, t) = X(x) * T(t), we substitute it into the heat equation:
T' * X - 3 * T * X'' = X'' * T + X' * T' + 1.
Dividing both sides by u(x, t) = X(x) * T(t), we get:
(T' / T) - 3 * (X'' / X) = (X'' / X) + (X' / X) + 1 / T.
Since the left side depends only on t and the right side depends only on x, they must be equal to a constant value, denoted as λ^2.
So, we have two separate ordinary differential
equations:
(T' / T) - 3 = (X'' / X) + (X' / X) + λ^2,
X'' - (λ^2 + 3)X = 0.
The first equation can be simplified:
T' / T = λ^2 + 3.
Solving it for T(t), we get:
T(t) = Ce^(λ^2 + 3)t.
Solving the second equation for X(x), we get:
X'' - (λ^2 + 3)X = 0.
This is again a homogeneous second-order linear differential equation with characteristic equation:
r^2 - (λ^2 + 3) = 0.
Solving this characteristic equation, we find two solutions:
r = ±√(λ^2 + 3).
The general solution for X(x) can be written as:
X(x) = A*e^(√(λ^2 + 3)x) + B*e^(-√(λ^2 + 3)x).
Combining the solutions for T(t) and X(x), we have:
u(x, t) = (A*e^(√(λ^2 + 3)x) + B*e^(-√(λ^2 + 3)x)) * Ce^(λ^2 + 3)t.
Now, we need to apply the initial condition u(x, 0) = (x^2 + 1) / 2 for x > 0.
Plugging in the values, we get:
(x^2 + 1) / 2 = (A*e^(√(λ^2 + 3)x) + B*e^(-√(λ^2 + 3)x)) * Ce^(λ^2 + 3) * 0.
Since the initial condition holds for x > 0, we can ignore the x terms. This leads to:
(x^2 + 1) / 2 = Ce^(λ^2 + 3) * 0.
From this, we obtain C = 0 for any λ.
Therefore, the general solution to the 1D heat equation with the given initial condition is:
u(x, t) = (A*e^(√(λ^2 + 3)x) + B*e^(-√(λ^2 + 3)x)) * e^(λ^2 + 3)t.
Please note that the solution involves a parameter λ, and specific values of A, B, and λ need to be determined based on the boundary conditions.
learn more about equation here: brainly.com/question/29657983
#SPJ11
Use Gaussian Elimination to solve the system of linear equations in the variables X1, X2, X3 given by x₁ + 2x₂ 3x3 = 9 x₂ + x3 = 0 2x1 4x₁x₂ + x3 = 4
Answers
By applying the Gaussian elimination method, we obtained the solution to the given system of linear equations as\(\(X_1 = \frac{1}{5}\), \(X_2 = -\frac{14}{5}\), and \(X_3 = \frac{14}{5}\).\)
To solve the given system of linear equations in the variables \(\(X_1\), \(X_2\), and \(X_3\)\) using Gaussian elimination, we start by creating the augmented matrix as shown below:
\(\[\begin{bmatrix}1 & 2 & 3 & 9 \\0 & 1 & 1 & 0 \\2 & 4 & 1 & 4\end{bmatrix}\]\)
Next, we aim to make the elements in the first column below the first row become zero. To do this, we multiply the first row by 2 and subtract the result from the third row:
\(\[\begin{bmatrix}1 & 2 & 3 & 9 \\0 & 1 & 1 & 0 \\0 & 0 & -5 & -14\end{bmatrix}\]\)
Then, we divide the third row by -5:
\(\[\begin{bmatrix}1 & 2 & 3 & 9 \\0 & 1 & 1 & 0 \\0 & 0 & 1 & -\frac{14}{5}\end{bmatrix}\]\)
Next, we proceed to make the elements in the second column below the second row become zero. We multiply the second row by -2 and add the result to the first row. Similarly, we multiply the second row by -1 and add the result to the third row:
\(\[\begin{bmatrix}1 & 0 & 1 & 9 \\0 & 1 & 1 & 0 \\0 & 0 & 1 & -\frac{14}{5}\end{bmatrix}\]\)
Finally, we make the elements in the third column below the third row become zero. We multiply the third row by -1 and add the result to the first row. We also multiply the third row by -1 and add the result to the second row:
\(\[\begin{bmatrix}1 & 0 & 0 & \frac{1}{5} \\0 & 1 & 0 & -\frac{14}{5} \\0 & 0 & 1 & \frac{14}{5}\end{bmatrix}\]\)
Therefore, the solution to the system of linear equations is:
\(\(X_1 = \frac{1}{5}\),\)
\(\(X_2 = -\frac{14}{5}\),\)
\(\(X_3 = \frac{14}{5}\)\)
Thus, by applying the Gaussian elimination method, we obtained the solution to the given system of linear equations as\(\(X_1 = \frac{1}{5}\), \(X_2 = -\frac{14}{5}\), and \(X_3 = \frac{14}{5}\).\)
To know more about Gaussian elimination method, click here
https://brainly.com/question/30400788
#SPJ11
Find the Laplace transform of 2 F(-) = 3 - 2 + S f(t) = 0, {%-u- t< 2 t² - 4t+6, t≥ 2
Answers
The Laplace transform of the given function f(t) is: L{f(t)} = 2/s³ - 4/s² + 6/s
To find the Laplace transform of the given function f(t), we'll split it into two parts based on the given conditions.
For t < 2, f(t) = 0. The Laplace transform of a constant function is given by:
L{0} = 0
For t ≥ 2, f(t) = t² - 4t + 6. We'll find the Laplace transform of each term separately using the standard formulas:
L{t²} = 2/s³
L{4t} = 4/s²
L{6} = 6/s
Now, we can combine the Laplace transforms of the two parts:
L{f(t)} = L{0} (for t < 2) + L{t² - 4t + 6} (for t ≥ 2)
= 0 + (2/s³ - 4/s² + 6/s)
= 2/s³ - 4/s² + 6/s
Therefore, the Laplace transform of the given function f(t) is:
L{f(t)} = 2/s³ - 4/s² + 6/s
To learn more about Laplace transform click here:
brainly.com/question/32716591
#SPJ11
The Laplace transform of the given function f(t) is: L{f(t)} = 2/s³ - 4/s² + 6/s
To find the Laplace transform of the given function f(t), we'll split it into two parts based on the given conditions.
For t < 2, f(t) = 0. The Laplace transform of a constant function is given by:
L{0} = 0
For t ≥ 2, f(t) = t² - 4t + 6. We'll find the Laplace transform of each term separately using the standard formulas:
L{t²} = 2/s³
L{4t} = 4/s²
L{6} = 6/s
Now, we can combine the Laplace transforms of the two parts:
L{f(t)} = L{0} (for t < 2) + L{t² - 4t + 6} (for t ≥ 2)
= 0 + (2/s³ - 4/s² + 6/s)
= 2/s³ - 4/s² + 6/s
Therefore, the Laplace transform of the given function f(t) is:
L{f(t)} = 2/s³ - 4/s² + 6/s
To learn more about Laplace transform click here: brainly.com/question/32716591
#SPJ11
Identify the area of sector AMC in terms of pi and rounded to the nearest hundredth.HELP PLS

Answers
Answer:
Step-by-step explanation:
The formula for the area of a sector is
\(A=\frac{\theta}{360}*\pi r^2\) where θ is the measure of the central angle and r is the radius.
Our central angle is a right angle and the radius is 4, so filling in the formula looks like this:
\(A=\frac{90}{360}*\pi (4)^2\) and
\(A=\frac{1}{4}*\pi (16)\)
16 divides by 4 evenly, so
A = 4π.in²
If we multiply 4 by the value of π and then round, that number, to the nearest hundredth, is
A = 12.57 in²
What is the value of n in the equation below?
12)
125
124
-20
9
O 20

Answers
Answer:
C. 9
Step-by-step explanation:
When dividing exponents with the same base, always subtract the top from the bottom, which in this case would be 9-5=4
The equation is an exponential equation, and the value of n in the equation is 9
How to determine the value of n?The equation is given as:
\(\frac{12^n}{12^5} = 12^4\)
Apply the law of indices, to the equation
\(12^{n-5} = 12^4\)
Cancel out the common base in the equation
n - 5 = 4
Add 5 to both sides
n = 9
Hence, the value of n in the equation is 9
Read more about equation solutions at:
https://brainly.com/question/14323743
#SPJ5
"whats the area of a circle with a circumference of 50.24 units"
pls help:)
Answers
Answer:
200.96 units^2
Step-by-step explanation:
50.24/Pi = 16 (diameter)
16/2=8 (radius)
area = Pi(r^2)
area = 3.14(8^2) = 200.96 units^2
If the circumference is pi times the diameter then you divide 50.24 by 3.14 and get 16. So the if the diameter is 16 the radius is 8. 8 squared is 64 times pi is 200.96. Hope that helps
Are the statements true or false?
Select True or False for each statement.

Answers
Answer:
True, False
Step-by-step explanation:
Answer:
the first one is true
and the second one is false
Step-by-step explanation:
multiplication goes in any other however division does not
example: 4×2=8 and 2×4 is also = 8
but 4÷2 =2 but 2÷4 is not equal to 2
Need help. How do I do this

Answers
9514 1404 393
Answer:
b
Step-by-step explanation:
Use the distance formula with the two points Q and P, then simplify and match the pattern of the answer.
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\\\d=\sqrt{(b-0)^2+(-c-(-a))^2}\\\\\boxed{d=\sqrt{b^2+(-c+a)^2}}\)
The value b goes in the green box.
PLEASE HELP!!!!!!!!! URGENT!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
the answer is
A. True
that is correct
Simplify the expression.
Write your answer without negative exponents.
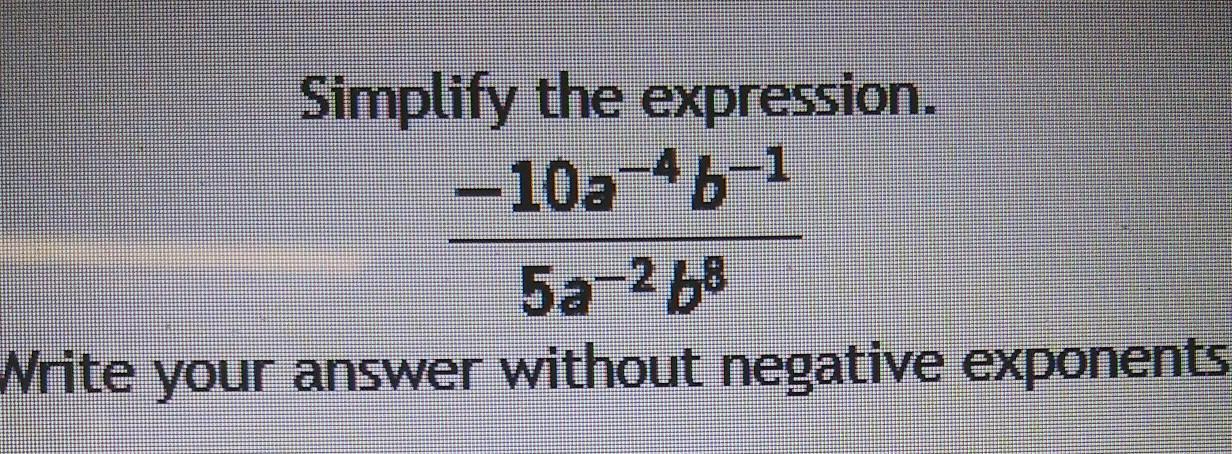
Answers
Answer: \(\frac{5a^2}{-10a^4b^9}\)
Step-by-step explanation:
Any negative exponent can be moved to the other side of the fraction as a positive exponent.
Thus, simply move the negative exponents to get: 5a^2/b*b^8*-10a^4. Then, use the exponent rule to get 5a^2/-10a^4b^9
Hope it helps <3
thank you for helping me

Answers
A I’m pretty sure
Explanation
Suppose that 18% of people own dogs. If you pick two people at random, what is the probability that they both own a dog
Answers
The probability that both randomly chosen people own a dog can be calculated using the concept of independent events. If 18% of people own dogs, it means that the probability of a person owning a dog is 0.18.
When picking the first person, there is a 0.18 probability that they own a dog. Now, assuming replacement (putting the person back before picking the second person), the probability that the second person also owns a dog is also 0.18.
To find the probability of both events occurring, we multiply the individual probabilities together: 0.18 * 0.18 = 0.0324.
Therefore, the probability that both randomly chosen people own a dog is 0.0324, which is equivalent to 3.24%. This means that if we were to repeat this random selection process many times, we would expect approximately 3.24% of the time to end up with two dog owners.
It's important to note that this calculation assumes independence between the events and replacement, meaning the probability of one person owning a dog does not affect the probability of the other person owning a dog.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
7. Determine the values that would make the fraction undefined:
\( \frac{ {x}^{2} + 2x - 8 }{ {x}^{2} - 3x - 10 } \)
Answers
\( \frac{ {x}^{2} + 2x - 8 }{ {x}^{2} - 3x - 10 } \)
Solution:To make a fraction undefined , you have to make the fraction's denominator equal to zero...let the denominator x² - 3x - 10 is f(x),
• Setting this factor equal to 0,
→ x² - 3x - 10 = 0
• By using Middle term splitting method,
→ x² - 5x + 2x - 10 = 0
→ (x² - 5x) + (2x - 10) = 0
• Taking common,
→ x( x - 5 ) + 2( x - 5 ) = 0
→ ( x - 5 ) ( x + 2 ) = 0
• Again, setting these factors equal to 0,
we get,( x - 5 ) = 0 and ( x + 2 ) = 0
→ x = 5 → x = -2
Hence, the values that would make the fraction undefined is x = 5,-2...
Hope this helps you!!Have a bless day!!Best of luck!! :)The values x = 5 and x = -2 would make the fraction undefined since they would result in a zero denominator.
To find the values that would make the fraction undefined, we need to identify any values of x that would make the denominator equal to zero.
The denominator of the fraction is (\(x^2 - 3x - 10\)). We need to solve the equation:
\(x^2 - 3x - 10 = 0\)
To factorize the quadratic equation, we look for two numbers that multiply to -10 and add up to -3. These numbers are -5 and 2:
(x - 5)(x + 2) = 0
Now, we can set each factor equal to zero and solve for x:
x - 5 = 0 => x = 5
x + 2 = 0 => x = -2
Therefore, the values x = 5 and x = -2 would make the fraction undefined since they would result in a zero denominator.
for such more question on fraction
https://brainly.com/question/1622425
#SPJ8
interpret the quote never confuse the size of your paycheck with the size of your talent
Answers
Note that the quote given above simply means that an employee or worker should never equate how much they earn to how much they are actually worth. This can take on different meanings depending on whether you want to assign a positive connotation to it or a negative one.
What is a quote in Literature?A quote is a verbatim reproduction of someone else's words that is generally surrounded by quotation marks and attributed to the original author or speaker.
Quoting implies paraphrasing someone else's remarks and citing the source. You must ensure the following when quoting a source:
The quoted content is surrounded by quotation marks or shown as a block quote.The original author is properly credited.The wording is exactly the same as the original.Learn more about Quotes:
https://brainly.com/question/24769951
#SPJ1
find the length of the missing side in the triangle use the 45-45-90 triangle theorem

Answers
Answer:
x = 7\(\sqrt{2}\) , y = 7
Step-by-step explanation:
the base angles of the triangle are congruent, both 45° , thus the triangle is isosceles with congruent legs , then
y = 7
using Pythagoras' identity in the right triangle
x² = 7² + 7² = 49 + 49 = 98 ( take square root of both sides )
x = \(\sqrt{98}\) = \(\sqrt{49(2)}\) = \(\sqrt{49}\) × \(\sqrt{2}\) = 7\(\sqrt{2}\)
9503×678+346÷45 help
Answers
Answer:
216,416
Step-by-step explanation:
helppppp my brain just doesn’t work today. I’ll brainlist.

Answers
Answer:
Number 6 is 1/6
Number 7 is 5/6
Number 8 is 3/6 or 1/2
Step-by-step explanation:
6. \(\frac{1}{6}\) chance of landing on a 2 because there are 6 sides and the probability is equal.
There is a 1/6 chance it will land on 1, 2, 3, 4, 5, and 6. So 1/6 is the answer.
7. \(\frac{5}{6}\) chance of not landing on 5. There are 5 "non-5" numbers. So 5/6 is the answer.
8. Let's see the odd numbers: 1, 2, 3, 4, 5, 6.
1, 3, and 5 are odd. So that's half of the numbers so the answer would be \(\frac{3}{6}\) or simplified to \(\frac{1}{2}\).
Hugo works at a shop
His normal rate of pay is £9. 00
The overtime rate is 1 1/3 times his normal hourly rate. Last Weekend, Hugo worked 7 hours on Saturday and 4 hours on Sunday
Answers
Answer:
To calculate Hugo's pay for the weekend, we need to calculate his regular pay and his overtime pay separately.
Regular pay for the weekend:
Hugo worked 7 hours on Saturday and 4 hours on Sunday, for a total of 11 hours. Since his normal rate of pay is £9.00 per hour, his regular pay for the weekend is:
7 hours x £9.00/hour (Saturday) + 4 hours x £9.00/hour (Sunday) = £63.00 + £36.00 = £99.00
Overtime pay for the weekend:
To calculate Hugo's overtime pay, we need to determine how many of his hours were worked at the overtime rate. The overtime rate is 1 1/3 times his normal hourly rate, which is:
1 1/3 x £9.00/hour = £12.00/hour
Hugo worked a total of 11 hours over the weekend, so we need to subtract his regular hours (which are paid at his normal rate) to find his overtime hours:
11 hours - (7 hours on Saturday + 4 hours on Sunday) = 0 overtime hours
Since Hugo did not work any overtime hours over the weekend, his overtime pay is zero.
Therefore, Hugo's total pay for the weekend is his regular pay of £99.00.
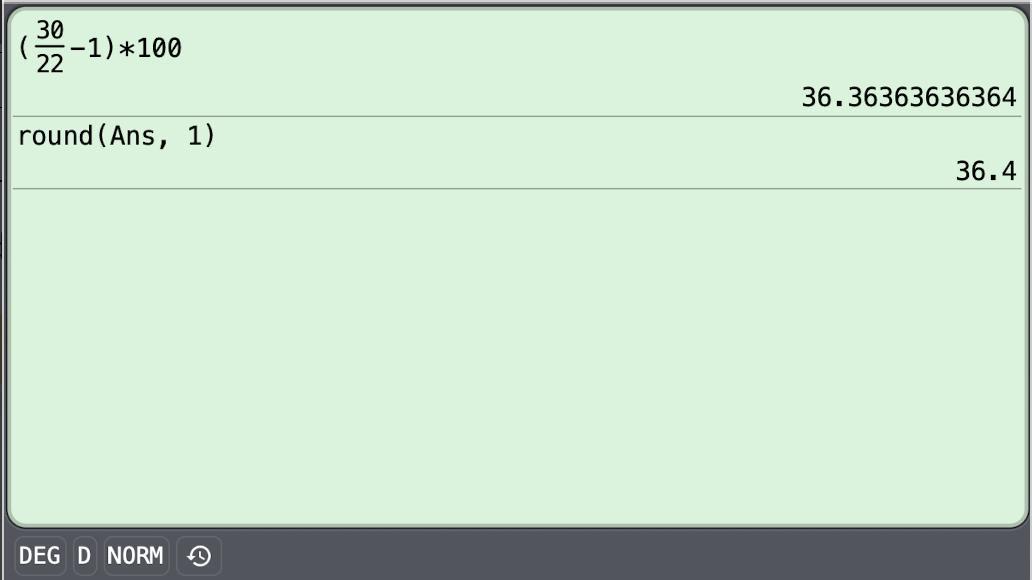
The value of a stock changes from $22 on Monday to $30 on Tuesday. Calculate the percent increase.
Answers
Answer:
36.4%
Step-by-step explanation:
You want the percentage change from $22 to $30.
Percentage changeThe percentage change is given by the formula ...
percent change = ((new value)/(old value) -1) × 100%
= (30/22 -1)(100%) ≈ 36.4%
The stock increased in value by about 36.4%.
<95141404393>
Heyy, If anyone can find the answer to this question, I’ll literally be in your DEBT

Answers
\(Answer: the\ number\ is\ \boxed{-26}\)
Step-by-step explanation:
\(2(n-4)=3(n+6)\\2(n)-2(4)=3(n)+3(6)\\2n-8=3n+18\\2n-8-18=3n+18-18\\2n-26=3n\\2n-26-2n=3n-2n\\-26=n\\Thus,\\n=-26\)
What the answer to this problem f(x)=-4x^2+12x-9
Answers
We are given the function;
\(f(x)=-4x^2+12x-9\)The input of this function as it is, is x. To evaluate the function at any given output we would simply replace/substitute the value of x with the value provided.
If for example, we are given the function and we have to evaluate its value at f(3), what we will simply do is replace x with two in the function. This is shown below;
\(\begin{gathered} f(x)=-4x^2+12x-9 \\ f(3)=-4(3)^2+12(3)-9 \\ f(3)=-4(9)+36-9 \\ f(3)=-36+36-9 \\ f(3)=-9 \end{gathered}\)Therefore, the value of the function at f(3) is -9.
This is basically the procedure we shall use when evaluating a function at any given output value.
Regular ice cream cones sell for 75¢ a scoop. Marty
and Ray each ordered double-scoop cones. Lisa
ordered a single scoop. How much did they spend in all?
Answers
Answer:
$3.75
Step-by-step explanation:

Which equation is equivalent to the formula
Y=a(x-h)2+ k
Answers
The equivalent equation in standard form is \(Y = ax^2 - 2ahx + ah^2 + k\)
Determining the equivalent equationThe formula \(Y=a(x-h)^2+ k\) is a quadratic function in vertex form, where (h,k) is the vertex of the parabola.
Now, to rewrite this formula in standard form, which is the form \(ax^2 + bx + c\), we can expand the square and simplify:
\(Y = a(x-h)^2 + k\\Y = a(x^2 - 2hx + h^2) + k\\Y = ax^2 - 2ahx + ah^2 + k\)
where a, b, and c are:
a = a
b = -2ah
c = \(ah^2\) + k
Therefore, the equivalent equation in standard form is:\(Y = ax^2 - 2ahx + ah^2 + k\)
Learn more on quadratic function on https://brainly.com/question/31300983
#SPJ1
A plane is on its approach to land on the runway. The jet's height above the ground is given in feet as a function of
the time in seconds. The following table tracks the plane as it lands:
t (in seconds) h (in feet)
0
4000
5
3500
10
3000
15
20
25
2500
2000
1500
Mark this and return
=
Ah
4
Calculate the slope. Use the formula
a. The plane is losing altitude.
b. The plane is gaining altitude.
c. The plane is remaining at a constant height.
d. The plane is losing altitude at a rate of 500 feet/second.
At
What is the significance of the sign of the slope?
Save and Exit
Next
Submit
Answers
The slope Using the formula will be h = -100t + 4000
This is a linear function because for every 5 seconds that pass, the height of the plane drops 500 feet, or -500 to be exact. So that's the slope of the line.
If we look at the table we can determine where the graph goes through the h axis. The h axis is the y axis, and the t axis is the x axis. So where the graph goes through the h axis is also the y-intercept.
If your teacher is any good at all, he/she would make sure that you understand beyond a shadow of a doubt that the y-intercept exists where x = 0. Looking at the table, where x (t) is 0, y (h) is 4000 feet.
Writing the linear equation then is super easy. In the form y = mx + b, we already know both the slope (-100) and the y-intercept (4000), so we fill in accordingly:
h = -100t + 4000 which appears to be choice a.
To learn more about linear function visit: https://brainly.com/question/21107621
#SPJ9
Can someone help solve num: 2

Answers
Answer:
The value of (y+6) is greater in 4(y+6).
Step-by-step explanation:
This is because the higher number of y's there are, the higher number you have to divide by, therefore in the end the number is smaller.
Two commercial flights per day are made from a small county airport. The airport manager tabulates the number of on-time departures for a sample of 200 days. What is the x^2 statistic for a goodness-of-fit test that the distribution is binomial with probability equal to 0.8 that a flight leaves on time?
Answers
The x² statistic for the goodness-of-fit test is approximately 104.15.
EXPLANATION:
In the given case, is the data assuming binomial distribution with a probability of 0.8 that a flight leaves on time. We have to find the x² statistic for the goodness-of-fit test.
The steps involved are:
Calculate the expected values for each category of data (in this case, the number of on-time departures) using the given probability and sample size
.Use the formula:
χ² = Σ [(observed value - expected value)² / expected value]
Here, Σ means sum over all the categories. Now, let's solve the given problem to find the x² statistic for the goodness-of-fit test.
Problem
Let p = probability that a flight leaves on time = 0.8
n = sample size = 200
Then, q = 1 - p = 0.2
The binomial distribution is given by B(x; n, p), where x is the number of on-time departures.
So, we can write:
B(x; 200, 0.8) = (200Cx)(0.8)x(0.2)200-x= (200! / x!(200 - x)!) × (0.8)x × (0.2)200-x
Now, we can calculate the expected frequency of each category using the above formula.
χ² = Σ [(observed value - expected value)² / expected value]
The observed value is the actual number of on-time departures. But, we don't have this information.
We are only given the sample size and the probability. Hence, we can use the expected frequency as the observed frequency.
The expected frequency is obtained using the formula mentioned above.
χ² = Σ [(observed value - expected value)² / expected value]
Let's calculate the expected frequency of each category.
Because the probability of success is 0.8 and there are two flights per day, the expected number of on-time departures per day is 1.6 (i.e., 2 × 0.8).
Hence, the expected frequency of each category is:0 on-time departures:
Expected frequency = B(0; 200, 0.8) = (200C0)(0.8)0(0.2)200-0 = (0.2)200 ≈ 2.56 on-time departures:
Expected frequency = B(1; 200, 0.8) = (200C1)(0.8)1(0.2)200-1 = 200(0.8)(0.2)199 ≈ 32.06 on-time departures:
Expected frequency = B(2; 200, 0.8) = (200C2)(0.8)2(0.2)200-2 = (199 × 200 / 2) (0.8)2 (0.2)198 ≈ 126.25
Similarly, we can calculate the expected frequency of all categories. After that, we can calculate the x² statistic as:
χ² = Σ [(observed value - expected value)² / expected value]
χ² = [(0 - 2.5)² / 2.5] + [(1 - 32.1)² / 32.1] + [(2 - 126.25)² / 126.25] + ... (all other categories)
χ² = 104.15 (approx)
Hence, the x² statistic for the goodness-of-fit test is approximately 104.15.
To know more about Binomial with Probaility:
https://brainly.com/question/30892543
#SPJ11
y=1/3x+11/15 find x if y=6
Answers
Step-by-step explanation:
plug in y
6=1/3x+11/15
multiply both sides by 15 to get rid of the fraction
90 = 5x +11
move terms to make them like terms
-5x =11- 90
-5x = -79
divide both sides by -5
evaluate for x
At a summer camp, the campers are divided into groups. Each group of 16 campers requires 2 cabins.
How many cabins are needed for 112 campers?
Answers
Answer:
896 cabins
Step-by-step explanation:
Given: Each group of 16 campers requires 2 cabins
To find: How many cabins are needed for 112 campers?
Solution: To find how many cabins are needed for 112 campers, divide 16 by 2
\(16\) ÷ \(2 = 8\)
Now, multiply the result by the campers
\(112\) × \(8 = 896\)
Therefore, 896 cabins are needed for 112 campers