Joe bought an apple tree that was 48 inches in height. He noticed that this tree grew approximately 4 inches in height each year.
Which statement best describes the function that could be used to model the height of the apple tree, h(t), as a function of time, t, in years.
~The height of the apple tree can be represented by a linear function, and the variable t is an exponent in the equation representing the function.
~The height of the apple tree can be represented by an exponential function, and the variable t is multiplied by 4 in the equation representing the function.
~The height of the apple tree can be represented by a linear function, and the variable t is multiplied by 4 in the equation representing the function.
~The height of the apple tree can be represented by an exponential function, and the variable t is an exponent in the equation representing the function.
Answers
Answer:
Step-by-step explanation:
8
Related Questions
1/4 (12x - 20) = -70
Answers
Divide each term in the bracket by 4:
=
3
x
−
2
Explanation:
Multiplying by
1
4
is the same as dividing by 4. - You are finding a quarter of something.
To find a quarter of the bracket, divide each coefficient by 4.
You will get two unlike terms so you will not be able to simplify them.
This is the reason why you cannot simplify inside the original bracket either.
Step-by-step explanation:
(2/3+5/2-7/3)+(3/2+7/3-5/6)
Answers
Answer:
after simplifying, we get,
23/6
Step-by-step explanation:
(2/3+5/2-7/3)+(3/2+7/3-5/6)
We simplify,
\((2/3+5/2-7/3)+(3/2+7/3-5/6)\\(2/3-7/3+5/2)+(3/2+7/3-5/6)\\(5/2-5/3)+(9/6+14/6-5/6)\\(15/6-10/6)+((9+14-5)/6)\\(15-10)/6+(23-5)/6\\5/6+18/6\\(5+18)/6\\23/6\)
Red tide" is a bloom of poison-producing algae–a few different species of a class of plankton called dinoflagellates. When the weather and water conditions cause these blooms, shellfish such as clams living in the area develop dangerous levels of a paralysis-inducing toxin. In Massachusetts, the Division of Marine Fisheries (DMF) monitors levels of the toxin in shellfish by regular sampling of shellfish along the coastline. If the mean level of toxin in clams exceeds 800 μg (micrograms) of toxin per kg of clam meat in any area, clam harvesting is banned there until the bloom is over and levels of toxin in clams subside. Describe both a Type I and a Type II error in this context, and state which error has the greater consequence.
Answers
This is the statistical question, specifically hypothesis testing and type I and type II errors.
A "Red tide" is a bloom of poison-producing algae involving dinoflagellates that can cause shellfish, such as clams, to develop dangerous levels of paralysis-inducing toxins. The Division of Marine Fisheries (DMF) monitors toxin levels in shellfish to determine if harvesting should be banned in specific areas.
In this context, a Type I error occurs when the DMF incorrectly bans clam harvesting in an area where the mean toxin level is not actually above 800 μg/kg of clam meat. This is a false positive, as the decision to ban harvesting is based on the assumption that the toxin levels are too high, even though they are not.
A Type II error occurs when the DMF fails to ban clam harvesting in an area where the mean toxin level is actually above 800 μg/kg of clam meat. This is a false negative, as the decision to allow harvesting is based on the assumption that the toxin levels are safe, even though they are not.
In this situation, a Type II error has the greater consequence, as it allows for the harvesting and consumption of toxic clams, posing a significant risk to public health. A Type I error, while economically harmful to the clam industry, does not put consumers at risk.
Learn more about type I and type II errors:
https://brainly.com/question/24320889
#SPJ11
Find 38% of 92. Round to the nearest whole number.
Answers
Answer:
38% of 92 rounded to the nearest whole number is 35.
Step-by-step explanation:
First we need to convert 38% into a decimal, 0.38.
Now we multiply 0.38 and 92.
So:
0.38 × 92 = 34.96
34.96 rounded to the nearest whole number is 35.
please helppppppppppp0

Answers
Answer:
a had 8 b had 10 total=180
Step-by-step explanation:
it's weird. I never really liked word problems but think through it. if each of them had to be the same amount of points, then what does bothe 10 AND 8 fit into?
80. simple.
so that means there were 8 true false questions in section a and 10 multiple choice in b and there was 160 points total because 80 +80 = 160
solve the equation by factoring plssss help ASAPPPP
4x^{2}-20x=0
Thanks UwU
Answers
Answer:
x = 0 and 5
Step-by-step explanation:
4x^2 - 20x = 0
Factor 4x
4x(x - 5) = 0
4x = 0 = > x = 0
x- 5 = 0 = > x = 5
a. Find the nth-order Taylor polynomials of the given function centered at the given point a, for n = 0, 1, and 2 b. Graph the Taylor polynomials and the function f(x)= 11 In (x), a = 1 The Taylor pol
Answers
The nth-order Taylor polynomials of f(x) = 11 ln(x) centered at a = 1 are P0(x) = 0, P1(x) = 11x - 11, and P2(x) = 11x - 11 - 11(x - 1)^2.
To find the nth-order Taylor polynomials of the function f(x) = 11 ln(x) centered at a = 1, we need to calculate the function value and its derivatives at x = 1.
For n = 0, the constant term, we evaluate f(1) = 11 ln(1) = 0.
For n = 1, the linear term, we use the first derivative: f'(x) = 11/x. Evaluating f'(1), we get f'(1) = 11/1 = 11. Thus, the linear term is P1(x) = 0 + 11(x - 1) = 11x - 11.
For n = 2, the quadratic term, we use the second derivative: f''(x) = -11/x^2. Evaluating f''(1), we get f''(1) = -11/1^2 = -11. The quadratic term is P2(x) = P1(x) + f''(1)(x - 1)^2 = 11x - 11 - 11(x - 1)^2.
To graph the Taylor polynomials and the function f(x) = 11 ln(x) on the same plot, we can choose several values of x and calculate the corresponding y-values for each polynomial. By connecting these points, we obtain the graphs of the Taylor polynomials P0(x), P1(x), and P2(x). We can also plot the graph of f(x) = 11 ln(x) to compare it with the Taylor polynomials. The graph will show how the Taylor polynomials approximate the original function around the point of expansion.
To learn more about Taylor polynomials click here: brainly.com/question/30481013
#SPJ11
What is the value of y in this triangle?
Enter your answer in the box.
y =

Answers
The value of y in the triangle is 64.
What is Triangle?
A triangle is a three-sided polygon that consists of three edges and three vertices.
We need to find the value of y,
The other two angles of triangle are 79⁰ and 37⁰
We have to use angle sum property of triangle
The sum of three angles of a triangle is 180⁰
y+ 79⁰+37⁰=180⁰
y+116⁰=180⁰
Subtract 116⁰ from both sides
y=180⁰- 116⁰
y=64⁰
Hence, the value of y in the triangle is 64.
To learn more on Triangles click:
https://brainly.com/question/2773823
#SPJ1
a circular pool is surrounded by a brick walkway 3 m wide. find the ra- dius of the pool if the area of the walk- way is 198 m*.
Answers
The radius of the pool is 9.01 m.
Given,
In the question:
A circular pool is surrounded by a brick walkway 3 m wide.
The area of the walk- way is 198 m^2.
To find the Radius of the pool.
Now, According to the question:
"Area of the circle bounded by the outside edge of the walkway" minus "area of the pool" = "area of the walkway".
Let R = Radius of the pool
Area of the circle bounded by the outside edge of the walkway is:
\(\pi\)(R +3)^2
Area of the pool is:
\(\pi R^2\)
Now, Our equation is:;
\(\pi\)(R +3)^2 - \(\pi R^2\) = 198
\(\pi\)((R+3)^2 - \(R^2\)) = 198
Open the inner bracket :
\(\pi\)(\(R^2+6R+9-R^2\)) = 198
\(\pi\)(6R +9) = 198
6R+9 = 198/\(\pi\)
6R = 198/\(\pi\) - 9
R = (198/\(\pi\) - 9)/6
R = (198/(3.14) - 9)/6
R = (63.057 - 9)/6
R = 54.057/6
R = 9.01 meters
Hence, The radius of the pool is 9.01 m.
Learn more about Radius of circle at:
https://brainly.com/question/28946570
#SPJ4
find a line through (-6,2,3) and parallel to the line 1/2x = 1/3y = z 1
Answers
The line through (-6, 2, 3) and parallel to the line 1/2x = 1/3y = z 1 can be represented by the equation 2x - 3y + z = -9.
To find a line through the point (-6, 2, 3) that is parallel to the line with the equation 1/2x = 1/3y = z 1, we need to determine the direction vector of the given line.
The direction vector of the line is given by the coefficients of x, y, and z. From the equation 1/2x = 1/3y = z 1, we can rewrite it as:
x/2 = y/3 = z/1
This implies that the ratios of x, y, and z are constant. Let's call this constant k.
x = 2k
y = 3k
z = k
So, the direction vector of the given line is (2, 3, 1).
Now, to find a line parallel to this direction vector and passing through the point (-6, 2, 3), we can use the point-slope form of a line:
(x - x₁)/a = (y - y₁)/b = (z - z₁)/c
Substituting the values, we have:
(x + 6)/2 = (y - 2)/3 = (z - 3)/1
This equation represents a line parallel to the given line and passing through the point (-6, 2, 3).
Please note that the equation can be simplified further by multiplying through by a common factor to eliminate fractions if desired.
For more such qustions on parallel
https://brainly.com/question/30097515
#SPJ8
Using the intermediate value theorem, determine, if possible, whether the function f has at least one real zero between a and b.f(x) = x^4 − 2x^2 − 8a = 2b = 5Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.a) By the intermediate value theorem, the function has at least one real zero between a and b because f(a) = _____ and f(b) = _____b) By the intermediate value theorem, the function does not have at least one real zero between a and b because f(a) = _____ and f(b) = _____c) It is impossible to use the intermediate value theorem in this case.
Answers
a) By the intermediate value theorem, the function has at least one real zero between a and b because f(a) = (a^4 - 2a^2 - 8) < 0 and f(b) = (b^4 - 2b^2 - 8) > 0. b) By the intermediate value theorem, the function does not have at least one real zero between a and b because f(a) = (a^4 - 2a^2 - 8) < 0 and f(b) = (b^4 - 2b^2 - 8) > 0. (c)The given statement is true "It is impossible to use the intermediate value theorem in this case." Because there are opposite signs of f(a) and f(b)
a) By the intermediate value theorem, the function has at least one real zero between a and b because f(a) = (a^4 - 2a^2 - 8) < 0 and f(b) = (b^4 - 2b^2 - 8) > 0.
Therefore, f(a) and f(b) have opposite signs and since f is a polynomial function and therefore continuous, by the intermediate value theorem, there exists at least one real zero of f between a and b.
So the correct choice is: a) By the intermediate value theorem, the function has at least one real zero between a and b because f(a) = (a^4 - 2a^2 - 8) < 0 and f(b) = (b^4 - 2b^2 - 8) > 0.
We cannot select b) because f(a) and f(b) have opposite signs and hence, f must have at least one zero between a and b. It is also not impossible to use the intermediate value theorem in this case.
To know more about intermediate value theorem:
https://brainly.com/question/30403106
#SPJ4
A scientist collects data on bacteria in a petri dish. She finds that the number of bacteria grows exponentially and can be modeled using the equation Y = 16 x 1.8^x, where x is the number of hours after she sets up the experiment and y is the number of bacteria in the dish. Complete the sentences to describe the model.
The scientist started with around __ bacteria in the petri dish.
Each hour the number of bacteria increases by about __%
Answers
The scientist started with around 16 bacteria in the petri dish.
Each hour, the number of bacteria increases by about 80%.
To describe the model in more detail:
The equation Y = 16 x 1.8ˣ represents an exponential growth model for the bacteria population in the petri dish.
The initial population of bacteria at the start of the experiment is approximately 16.
As time progresses, represented by the variable x (the number of hours), the number of bacteria increases exponentially.
The term 1.8ˣ in the equation represents the exponential growth factor. With each passing hour, the number of bacteria multiplies by a factor of 1.8.
This indicates that the bacteria population experiences rapid growth, increasing by 80% per hour.
Exponential growth models are characterized by a constant relative growth rate the population size grows at an increasingly faster pace over time.
The bacteria population in the petri dish exhibits such growth dynamics, with the number of bacteria multiplying by 1.8 every hour.
For similar questions on bacteria
https://brainly.com/question/30684301
#SP8
(-12) Divided by 6 +2
Answers
Answer:
0
I hope its zero.........
Answer:
-1.5
Step-by-step explanation:
-12/6+2
-12/8
-1.5
A quilt is designed using a square pattern. each square contains two rectangles. each rectangle contains a shaded rhombus. each rectangle contains a shaded rhombus. the left angle is 50 degrees and the top angle is (2 x 20) degrees. what is the value of x? 50 55 125 145
Answers
Based on the calculations, the value of x in this rhombus is equal to: B. 55.
How to determine the value of x?Since the opposite angles in a rhombus are always congruent, the sum of each angle in any rhombus must be equal to 360 degrees.
From the image of the rhombus, we can deduce the following parameters:
Adjacent angles = 2x + 20 and 50 degrees.
Opposite angles = 2x + 20 and 50 degrees.
Adding the angles, we have:
2x + 20 + 2x + 20 + 50 + 50 = 360
4x + 140 = 360
4x = 360 - 140
4x = 220
x = 220/4
x = 55°
Read more on rhombus here: https://brainly.com/question/11586845
#SPJ4

help me pls!!!! *\-(-_-)-/*

Answers
what is equivalent to 5/4?
Answers
Answer:
10/8 15/12 20/16, 25/20, 30/24, 35/28, 40/32, 45/36, 50/40, 55/44, 60/48, 65/52, 70/56, 75/60, 80/64, 85/68, 90/72, 95/76, 100/80
There are probably hundreds of fractions that are equivalent to 5/4 but i am going to list 3-
1. 10/8
2. 15/12
3. 20/16
how much is 10% of 10 leters of milk
Answers
Answer:100%
Step-by-step explanation:
Answer: 100%
Step-by-step explanation:
Exercise 7.28. Let X1, X2, X3 be independent Exp(4) distributed random vari ables. Find the probability that P(XI < X2 < X3).
Answers
The probability that P(X1 < X2 < X3) is 1/8.
We can solve this problem using the fact that if X1, X2, X3 are independent exponential random variables with the same rate parameter λ, then the joint density function of the three variables is given by:
f(x1, x2, x3) = λ^3 e^(-λ(x1+x2+x3))
We want to find the probability that X1 < X2 < X3. We can express this event as the intersection of the following three events:
A: X1 < X2
B: X2 < X3
C: X1 < X3
Using the joint density function above, we can compute the probability of each of these events using integration. For example, the probability of A is:
P(X1 < X2) = ∫∫ f(x1, x2, x3) dx1 dx2 dx3
= ∫∫ λ^3 e^(-λ(x1+x2+x3)) dx1 dx2 dx3 (integration over the region where x1 < x2)
= ∫ 0^∞ ∫ x1^∞ λ^3 e^(-λ(x1+x2+x3)) dx2 dx3 dx1
= ∫ 0^∞ λ^2 e^(-2λx1) dx1 (integration by substitution)
= 1/2
Similarly, we can compute the probability of B and C as:
P(X2 < X3) = 1/2
P(X1 < X3) = 1/2
Note that these probabilities are equal because the three exponential random variables are identically distributed.
Now, to compute the probability of the intersection of these events, we can use the multiplication rule:
P(X1 < X2 < X3) = P(A ∩ B ∩ C) = P(A)P(B|A)P(C|A∩B)
Since A, B, and C are independent, we have:
P(B|A) = P(B) = 1/2
P(C|A∩B) = P(C) = 1/2
Therefore:
P(X1 < X2 < X3) = (1/2)(1/2)(1/2) = 1/8
Thus, the probability that X1 < X2 < X3 is 1/8.
To learn more about Probability
https://brainly.com/question/24870672
#SPJ11
An automobile manufacturer is automating the placement of certain components on the bumpers of a limited-edition line of sports cars. The components are color-coordinated, so the assembly robots need to know the color of each car in order to select the appropriate bumper component. Models come in only four colors: blue, green, red, and white. You are hired to propose a solution based on imaging. How would you solve the problem of determining the color of each car, keeping in mind that cost is the most important consideration in your choice of components.
Please explain in detail and do not copy other answers already on here
Answers
To solve the problem of determining the color of each car for automated placement of components on the bumpers, propose a cost-effective solution for determining the color of sports cars' bumpers using imaging. Implement a vision system to capture car images, apply image processing and color classification algorithms, select components based on color, and integrate with assembly robots.
To solve the problem of determining the color of each car for automated placement of components on the bumpers, an imaging-based solution can be employed with cost-effectiveness as a primary consideration. Here's a proposed solution:
1. Use a vision system: Implement a camera-based vision system that captures images of the cars as they move along the assembly line. The system should be capable of capturing accurate color information.
2. Image processing: Apply image processing techniques to analyze the captured images and extract color information from specific regions of interest (such as the bumper area).
3. Color classification: Utilize color classification algorithms to determine the color of each car based on the extracted color information. This can involve comparing pixel values or using machine learning algorithms to classify the colors accurately.
4. Component selection: Associate each color classification with the appropriate bumper component. Set up a system that selects the corresponding component based on the determined car color.
5. Cost optimization: Consider the cost aspect while selecting the components. Evaluate the cost of each component and prioritize cost-effective options without compromising quality or performance.
6. Integration: Integrate the imaging-based color detection system with the assembly robots to ensure seamless component selection and placement based on the determined color.
7. Testing and refinement: Conduct extensive testing and validation of the system to ensure accurate color detection and component selection. Refine the algorithms and processes as necessary to improve performance and reliability.
By combining imaging technology, image processing, color classification, cost optimization, and integration with the assembly process, this proposed solution aims to automate the selection of color-coordinated components for the sports cars' bumpers efficiently and cost-effectively.
For more questions on automated placement of components:
https://brainly.com/question/10656823
#SPJ8
Find all possible inflection points of f(x) = -x^4 + 24x^2. Are there any actual inflection points of f(x)?
Answers
Given the function:
\(f(x)=-x^4+24x^2\)You need to remember that the Inflection Points of a function are where it changes its concavity.
By definition, a function can have more than one inflection point:
1. You need to find:
\(f^{\prime}(x)\)Remember the following Derivatives Power Rule:
\(\frac{d}{dx}(x^n)=nx^{n-1}\)You get:
\(f^{\prime}(x)=-4(x^{4-1})+(2)(24)(x^{2-1})\)\(f^{\prime}(x)=-4x^3+48x\)2. Find the second derivative by derivating the first derivative. This is:
\(f^{^{\prime}^{\prime}}(x)=(-4)(3)x^{3-1}+48\)\(f^{^{\prime\prime}}(x)=-12x^2+48\)3. Find the third derivative by derivating the second derivative:
\(f^{^{\prime^{\prime}^{\prime}}}(x)=(-12)(2)x^\)\(f^{^{\prime^{\prime}^{\prime}}}(x)=-24x\)4.Find the roots of the second derivative:
- Set up that:
\(-12x^2+48=0\)- And solve for "x":
\(\begin{gathered} -12x^2=-48 \\ \\ x=\sqrt{\frac{-48}{-12}} \\ \\ x_1=2 \\ x_2=-2 \end{gathered}\)5. Substitute each root into the third derivative and evaluate:
\(f^{^{\prime^{\prime}^{\prime}}}(2)=-24(2)=-48\)It is less than zero, therefore there is an inflection point in that x-value.
\(f^{^{\prime^{\prime\prime}}}(-2)=-24(-2)=48\)It is positive output value, therefore there is an inflection point in that x-value.
6. Substitute those x-values into the original function and evaluate:
\(f(2)=-(2)^4+24(2)^2=80\)\(f(-2)=-(-2)^4+24(-2)^2=80\)Therefore, the inflections points are:
\(\begin{gathered} (-2,80) \\ (2,80) \end{gathered}\)Hence, the answer is:
There are two inflection points:
\(\begin{gathered} (-2,80) \\ (2,80) \end{gathered}\)Amira wants to ride her bicycle 48 miles this week. She has already ridden 18 miles. If she rides for 5 more days, write and solve an equation that can be used to determine x, the average number of miles she would have to ride each day to meet her goal.
PLEASE WRITE AN EQUATION
Answers
Answer:
6 miles bicycleriding per day
Step-by-step explanation:
5x+18=48
5x=48-18
5x=30
x=30/5
x=6
Solved X = 6
Step by step
Using y intercept form y=mx + b
Y is the total goal of 48 miles
M is rate, here it is 5 days
X is the unknown miles
B is the y intercept or set amount/starting point, which is the 18 already ridden
So
48 = 5x + 18
Solve
Subtract 18 from both sides to isolate X
48 -18 = 5x +18 - 18
30 = 5x
Divide both sides by 5 to solve for x
30/5 = 5/5 x
6 = x
Now we check our work
48 = 5x + 18
48 = (5) (6) + 18
48 = 30 + 18
48 = 48
Problem solved!
A sphere has a diameter of 12 ft. What is the volume of the sphere? Give the exact value in terms of pi
Answers
is the answer hope that helps
Calculate each Poisson probability: a. P(X = 7), λ = 6 (Round your answer to 4 decimal places.) b. P(X = 11), λ = 12 (Round your answer to 4 decimal places.) c. P(X = 6), λ = 8 (Round your answer to 4 decimal places.)
Answers
P(X = 7), λ = 6: The Poisson probability of X = 7, with a parameter (λ) value of 6, is 0.1446. P(X = 11), λ = 12: The Poisson probability of X = 11, with a parameter (λ) value of 12, is 0.0946. P(X = 6), λ = 8: The Poisson probability of X = 6, with a parameter (λ) value of 8, is 0.1206.
The Poisson probability is used to calculate the probability of a certain number of events occurring in a fixed interval of time or space, given the average rate of occurrence (parameter λ). The formula for Poisson probability is P(X = k) = (e^-λ * λ^k) / k!, where X is the random variable representing the number of events and k is the desired number of events.
To calculate the Poisson probabilities in this case, we substitute the given values of λ and k into the formula. For example, for the first case (a), we have λ = 6 and k = 7: P(X = 7) = (e^-6 * 6^7) / 7!
Using a calculator, we can evaluate this expression to find that the probability is approximately 0.1446. Similarly, for case (b) with λ = 12 and k = 11, and for case (c) with λ = 8 and k = 6, we can apply the same formula to find the respective Poisson probabilities.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
Solve: XY-5 X= 5 Y=2
A. 10
B. 5
C. 15
D. 2
Answers
Answer:
A
Step-by-step explanation:
Which comic section is represented by the following equation ?
circle
ellipse
parabola
hyperbola
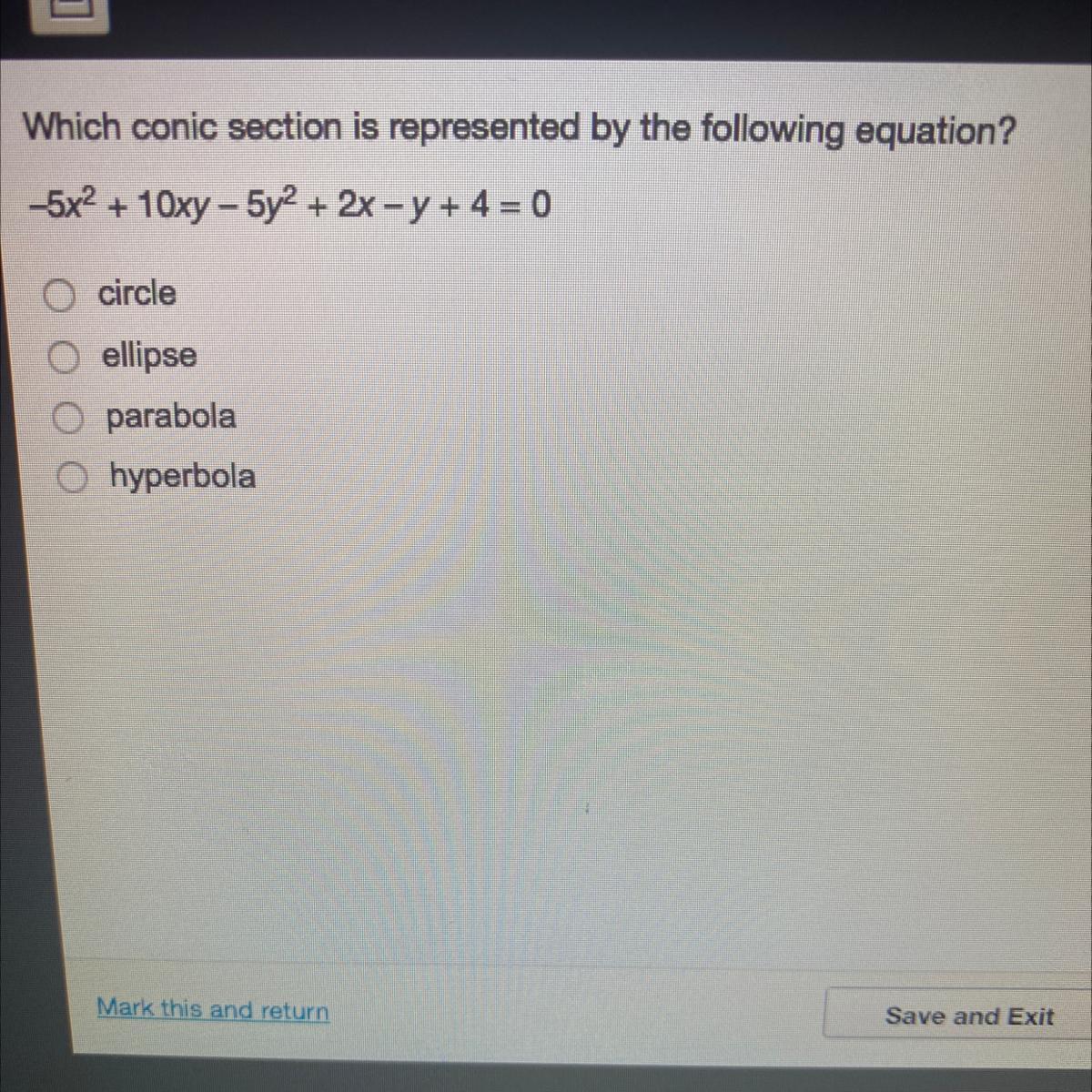
Answers
Answer:
hyperbola
Step-by-step explanation:
Sana makatulong
can someone help me I'm doing my packet and the quest is hard

Answers
A train travels at a constant rate of 145 miles per hour.
a. What is the equation for this scenario?
b. A second train is traveling 300 miles in 2 hours. Which train is traveling faster? How do you
know?
Answers
Answer:
a. r = d/t, 145(rate) = 145(distance)/1(time)
b. The second train is travelling faster
The first train has a rate of 145 mph the second has a rate of 150 mph since r = 300 miles/2 hours = 150
Therefore the second train has a rate of 150 mph while the first train has rate of 145 mph
If I am earning £4.99 per hour at work , and I work for 38 hours a week how much would I earn in 6 months
Answers
Answer:
like 1000 maybe?
I think that's like a tough estimate
Answer:
4,930
Step-by-step explanation:
38 x 4.99= 189.62
since there are about 26 weeks in 6 months-
189.62 x 26 = 4,930.12
Given 3x 2
y+2xy−16=0, use implicit differentiation then solve for y ′
.
Answers
Therefore, the derivative of y with respect to x, y', is given by:\(y' = (-2y - 6xy) / (3x^2 + 2x)\).
To solve for y' using implicit differentiation, we will differentiate both sides of the equation with respect to x, treating y as a function of x. Let's begin:
Differentiating \(3x^2y + 2xy - 16 = 0\) with respect to x:
\(d/dx(3x^2y) + d/dx(2xy) - d/dx(16) = 0\)
Applying the product rule and chain rule:
\((6xy + 3x^2(dy/dx)) + (2y + 2x(dy/dx)) - 0 = 0\)
Combining like terms:
\(6xy + 3x^2(dy/dx) + 2y + 2x(dy/dx) = 0\)
Rearranging the equation and isolating dy/dx:
\(3x^2(dy/dx) + 2x(dy/dx) = -6xy - 2y\)
Factoring out dy/dx:
\((3x^2 + 2x)(dy/dx) = -2y - 6xy\)
Dividing both sides by \((3x^2 + 2x):\)
\(dy/dx = (-2y - 6xy) / (3x^2 + 2x)\)
To know more about derivative,
https://brainly.com/question/28176176
#SPJ11
3 Burgers and 5 tacos for 24.75, a burger is the price of two tacos.Find the cost of a burger and the cost of a taco
Answers
Let:
• b ,be the cost of a burger
,• t, be the cost of a taco
"3 Burgers and 5 tacos for 24.75" means:
\(3b+5t=24.75\)And "a burger is the price of two tacos" means:
\(b=2t\)Substituting in the first equation and solving for t, we get:
\(\begin{gathered} 3b+5t=24.75 \\ \rightarrow3(2t)+5t=24.75 \\ \rightarrow6t+5t=24.75 \\ \rightarrow11t=24.75 \\ \rightarrow t=\frac{24.75}{11} \\ \Rightarrow t=2.25 \end{gathered}\)Using this in our second equation,
\(\begin{gathered} b=2t \\ \rightarrow b=2(2.25) \\ \Rightarrow b=4.50 \end{gathered}\)We get that burgers cost $4.50 and that tacos cost $2.25
Answer:
Burgers=4.50
tacos= 2.25
Step-by-step explanation:
3 burgers
5 tacos
=$24.75/(B+t2)
3+5t=24.75
3(2t)+5t=24.75
6t+5t=24.75
11+=24.75
tacos=2.25
Burgers = 2.25 x 3