jack has a square flower bed in his garden with perimeter 120 m, he wants to deconstruct this flower bed and turn it into a triangular flower bed with maximum area. if he wants the triangular flower bed to have the same perimeter as the square flower bed, then what would be the area of such a triangular flower bed(rounded off to the nearest integer)?
Answers
To find the maximum area for the triangular flower bed with the same perimeter as the square flower bed, we can use the concept of an equilateral triangle.
Let's denote the side length of the square flower bed as 's'. Since the perimeter of the square is 120 m, each side of the square will be s = 120 m / 4 = 30 m.
Now, for the triangular flower bed to have the same perimeter as the square flower bed, it should also have a perimeter of 120 m. In an equilateral triangle, all three sides are equal in length.
Let's denote the side length of the equilateral triangle as 't'. Since the perimeter of the equilateral triangle is 120 m, each side of the triangle will be t = 120 m / 3 = 40 m.
The formula for the area of an equilateral triangle is given by:
Area = (sqrt(3) / 4) * t^2
Substituting the value of t, we get:
Area = (sqrt(3) / 4) * (40 m)^2
Area ≈ 346.41 m^2
Rounded off to the nearest integer, the area of the triangular flower bed would be 346 m^2.
Related Questions
HELP ASAP PLEASE
I JUST NEED WORK SHOWN BUT ASAP

Answers
Answer:
s = 25.33m
θ = 60.65°
12.37m
A = 160m^2
Step-by-step explanation:
The pyramid has a side base of 35m and a height of 22m.
side base = b = 35m
height of the pyramid = h = 22m
To calculate the slant edge of the pyramid, you first calculate the diagonal of the squared base of the pyramid.
You use the Pythagoras theorem:
\(d=\sqrt{(\frac{35}{2})^2+(\frac{35}{2})^2}=24.74\)
With the half of the diagonal and the height, and by using again the Pythagoras theorem you can calculate the slat edge:
\(s=\sqrt{(\frac{24.74}{2})^2+(22)^2}=25.23\)
The slant edge of the pyramid is 25.33m
The angle of the base is given by:
\(\theta=sin^{-1}(\frac{h}{s})=sin^{-1}(\frac{22}{25.23})=60.65\°\)
The angle of the base is 60.65°
The distance between the corner of the pyramid and its center of its base is half of the diagonal, which is 24.74/2 = 12.37m
The area of one side of the pyramid is given by the following formula:
\(A=\frac{(b/2)l}{2}\) (1)
l: height of the side of pyramid
then, you first calculate l by using the information about the side base and the slant.
\(l=\sqrt{s^2-(\frac{b}{2}^2)}=\sqrt{(25.33)^2-(\frac{35}{2})^2}\\\\l=18.31m\)
Next, you replace the values of l and b in the equation (1):
\(A=\frac{(35/2)(18.31)}{2}=160m^2\)
The area of one aside of the pyramid is 160m^2
Side BC is 4 meters long. Side CD is twice the length of the side BC. What is the length of side LM. Explain your reasoning.

Answers
Answer:
LM = 18
Step-by-step explanation:
BC = 4
CD is twice that, so CD is 8
Now, remembering that the area of ABCD = 32 and JKLM = 72, divide 72 by 32.
You get 2.25. This is how much bigger JKLM is than ABCD.
Using that, multiply the length of CD (which is 8) by 2.25 to get the length of LM.
You'll get 18.
Hope this helps!
min ti x₁ = x₂-u x₂ = u -144²1 (x₁, x₂) arbitrary starting point. Let (0,0) be the Check whether situation (x₁, x₂)→ (0,0) shortest time is met. the beginning of the the coordinate. generality condition of the
Answers
It appears that the system dynamics can be manipulated through the control input u to minimize the time required for convergence to the origin (0,0).
Here, we have,
given that,
min t_i
x₁ = x₂-u
x₂ = u
-1 ≤ u ≤ 1, (x₁, x₂) are arbitrary starting point.
and origin (0,0) be the begging of the coordinate.
also given that, (x₁, x₂)→ (0,0)
so, min t_i at origin (0,0) = t
Therefore, the generality condition of the situation does not met.
so, we get,
The given system can be represented by the following equations:
x₁' = x₂ - u
x₂' = u
To analyze the behavior of the system, we can examine the dynamics of each variable separately.
For x₁:
x₁' = x₂ - u
The equation implies that the rate of change of x₁ is dependent on x₂ and the input u. The term (-u) acts as a control input that can affect the dynamics of x₁. If we choose an appropriate control input u, we can manipulate the rate of change of x₁ and potentially minimize the time required to reach the origin.
For x₂:
x₂' = u
The equation for x₂ indicates that the rate of change of x₂ is solely determined by the input u. The variable x₂ can be directly controlled by the input u, allowing us to influence its behavior and potentially expedite convergence.
Based on the given equations, it appears that the system dynamics can be manipulated through the control input u to minimize the time required for convergence to the origin (0,0).
By carefully selecting the control input, it is possible to achieve the shortest time to reach the origin from any arbitrary starting point (x₁, x₂).
To learn more on rate of change click:
https://brainly.com/question/32765463
#SPJ4
Find the constants m and b in the linear function f(x)=mx+b so that f(7)=9 and the straight line represented by f has slope −3.
m=
b=
Answers
To find the constants m and b in the linear function f(x) = mx + b, we can use the given conditions f(7) = 9 and a slope of -3.
The value of f(7) represents the y-coordinate of the point on the line when x = 7. So, substituting x = 7 into the equation, we get 9 = 7m + b.
The slope of a linear function is given by the coefficient of x, which in this case is -3. So, we have m = -3.
Now, we can substitute the value of m into the equation obtained from f(7). We get 9 = 7(-3) + b, which simplifies to 9 = -21 + b.
Solving for b, we find b = 30.
Therefore, the constants for the linear function f(x) = mx + b that satisfy the given conditions are m = -3 and b = 30.
learn more about linear function here:
https://brainly.com/question/21107621
#SPJ11
A dog food company makes two kinds of canned dog food. a
can of the big-n-beefy brand contains 8 oz. of beef byproducts
and 4 oz. of meal. a can of the grand gourmet brand contains 5
oz. of beef byproducts and 7 oz. of meal. the machine that
grinds the beef byproducts can grind 340 oz. per hour while the
machine grinding the meal can grind 330 oz. per hour.
let b represent the number of cans of big-n-beefy that are
produced each hour, and g represent the number of cans of
grand gourmet produced each hour.
identify the inequalities that represent constraints on the
number of cans of dog food this company can produce each
hour. select all that apply.
Answers
Inequalities to represent the constraints for the number of cans of dog food is given by 8b + 4g < 340 , 5b + 7g < 330.
As given in the question,
Let the number of cans of dog food of big-n beefy produced in each hour is represented by 'b'
And the number of cans of dog food of grand gourmet produced in each hour is represented by 'g'
Big-n- beefy contains :
8oz. of beef and 4oz. of meal in 340oz. per hour
Grand gourmet contains :
5oz. of beef and 7oz. of meal in 330oz. per hour
Inequalities to represent the constraint are given by :
8b + 4g < 340
5b + 7g < 330
Therefore, the inequalities to represents the constraints produced number of cans food in each hour is given by :
8b + 4g < 340 , 5b + 7g < 330.
Learn more about inequalities here
brainly.com/question/28823603
#SPJ4
Please help me with this!

Answers
xz = z^4\xy^2
answer:
I believe it's D
please help me find the values of x and y

Answers
Answer: A = X + Y; B = X xor Y. The task is to make X as minimum as possible.
Step-by-step explanation:
Polygons in the coordinate

Answers
In order to know if a triangle is a right triangle on a coordinate plane, you can find the lengths of all three sides of the triangle using the distance formula and apply the Pythagorean theorem.
How to know if it's a triangleFind the lengths of the three sides of the triangle using the distance formula.
Once you have the lengths of the sides, check if any of the three sides satisfy the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides. In other words, if a² + b² = c², where c is the longest side, then the triangle is a right triangle.
If one of the sides satisfies the Pythagorean theorem, then the triangle is a right triangle.
Learn more about triangle on
https://brainly.com/question/17335144
#SPJ1
B. Optimizing Multivariable Functions Optimize z = 3x² - xy + 2y² - 4x - 7y + 12. 1. Find the critical points at which the function may be optimized. 2. Determine whether at the computed points, the
Answers
The critical points are (2,1) and (0,0). Given, z = 3x² - xy + 2y² - 4x - 7y + 12.1. Find the critical points at which the function may be optimized.
To find the critical points, we need to solve the following system of equations: ∂z/∂x = 0, ∂z/∂y = 0∂z/∂x = 6x - y - 4 = 0∂z/∂y = -x + 4y - 7 = 0By solving these equations, we get two critical points: (2,1) and (0,0).2. Determine whether at the computed points, the function takes on its maximum or minimum value.
To determine whether each critical point is a maximum, minimum, or saddle point, we need to compute the second partial derivatives of z: ∂²z/∂x² = 6, ∂²z/∂y² = 4, ∂²z/∂x∂y = -1At the point (2,1), the second partial derivatives satisfy the condition (∂²z/∂x²)(∂²z/∂y²) - (∂²z/∂x∂y)² = (6)(4) - (-1)² = 25 > 0 and ∂²z/∂x² > 0, so z has a minimum value at this point.At the point (0,0), the second partial derivatives satisfy the condition (∂²z/∂x²)(∂²z/∂y²) - (∂²z/∂x∂y)² = (6)(4) - (-1)² = 25 > 0 and ∂²z/∂x² > 0, so z has a minimum value at this point.Therefore, the function z = 3x² - xy + 2y² - 4x - 7y + 12 is optimized at (2,1), where the minimum value is z = 3(2)² - (2)(1) + 2(1)² - 4(2) - 7(1) + 12 = -10.
To know more about critical points visit:
https://brainly.com/question/32077588
#SPJ11
All three members of the Harrison family want to take a cruise with Luxury Starline. Estimate how much the family would spend if a cruise costs $1,825 per person by rounding the cost per person to the nearest thousand. $
Answers
In the word problem ,the total cost for cruise for total family is $5475.
What is word problem?
Word problems are often described verbally as instances where a problem exists and one or more questions are posed, the solutions to which can be found by applying mathematical operations to the numerical information provided in the problem statement. Determining whether two provided statements are equal with respect to a collection of rewritings is known as a word problem in computational mathematics.
Here the Total members of the Harrison family = 3
Cost of cruise per person = $1825
Now, Total cost for cruise of Harrison family is,
=> Total members × Cost per person
=> 3 × 1825
=> $5475
Hence the total cost for cruise for total family is $5475.
To learn more about word problem refer the below link
https://brainly.com/question/21405634
#SPJ1
6 Q Find the area of the circle pictured above. Round your answer to the nearest tenth
Answers
Answer:
28.3 units^2
Explanation:
The area A of the circle is given by the formula
\(A=\pi(\frac{d}{2})^2\)where
π = 3.1415..
d = diameter of the circle.
Now, in our case d = 6; therefore,
\(A=\pi(\frac{6}{2})^2\)\(A=(3.1415)(3)^2\)\(A=(3.1415)(9)\)\(A=28.274\)Rounded to the nearest tenth this is
\(A=28.3\)3.38 If the joint probability distribution of X and Y is given by
f(x,y)= x + y /30, for x =0 ,1,2,3; y =0 ,1,2,find
(a) P(X ≤ 2,Y = 1); (b) P(X>2,Y ≤ 1); (c) P(X>Y); (d) P(X + Y = 4).
3.46 Referring to Exercise 3.38, find (a) the marginal distribution of X; (b) the marginal distribution of Y .
Answers
a)The probability that X is less than or equal to 2 and Y is equal to 1 is 1/5.
b) the probability that X is greater than 2 and Y is less than or equal to 1 is 2/15.
c)the probability that X is greater than Y is 2/5.
d)the probability that X plus Y is equal to 4 is 2/5.
(a) To find P(X ≤ 2, Y = 1), we need to sum up the joint probabilities for all values of X that are less than or equal to 2 and Y = 1:
P(X ≤ 2, Y = 1) = f(0,1) + f(1,1) + f(2,1)
= (0+1)/30 + (1+1)/30 + (2+1)/30
= 6/30
= 1/5
Therefore, the probability that X is less than or equal to 2 and Y is equal to 1 is 1/5.
(b) To find P(X > 2, Y ≤ 1), we need to sum up the joint probabilities for all values of X that are greater than 2 and Y is less than or equal to 1:
P(X > 2, Y ≤ 1) = f(3,0) + f(3,1)
= (3+0)/30 + (3+1)/30
= 4/30
= 2/15
Therefore, the probability that X is greater than 2 and Y is less than or equal to 1 is 2/15.
(c) To find P(X > Y), we need to sum up the joint probabilities for all values of X that are greater than Y:
P(X > Y) = f(1,0) + f(2,0) + f(2,1) + f(3,0) + f(3,1) + f(3,2)
= (1+0)/30 + (2+0)/30 + (2+1)/30 + (3+0)/30 + (3+1)/30 + (3+2)/30
= 12/30
= 2/5
Therefore, the probability that X is greater than Y is 2/5.
(d) To find P(X + Y = 4), we need to sum up the joint probabilities for all pairs of X and Y that add up to 4:
P(X + Y = 4) = f(1,3) + f(2,2) + f(3,1)
= (1+3)/30 + (2+2)/30 + (3+1)/30
= 12/30
= 2/5
Therefore, the probability that X plus Y is equal to 4 is 2/5.
(a) To find the marginal distribution of X, we need to sum up the joint probabilities for each possible value of X:
P(X = 0) = f(0,0) + f(0,1) + f(0,2) = (0+0)/30 + (0+1)/30 + (0+2)/30 = 3/30 = 1/10
P(X = 1) = f(1,0) + f(1,1) + f(1,2) = (1+0)/30 + (1+1)/30 + (1+2)/30 = 6/30 = 1/5
P(X = 2) = f(2,0) + f(2,1) + f(2,2) = (2+0)/30 + (2+1)/30 + (2+2)/30 = 9/30 = 3/10
P(X = 3) = f(3,0) + f(3,1) + f(3,2) = (3
Click the below link, to learn more about probability distribution:
https://brainly.com/question/14210034
#SPJ11
A school drama department sells 40 more student tickets than adult tickets. Charging $8 for adult tickets and $6 for student tickets, the drama department raises a total of $1,920 in ticket sales . Let x represent the number of adult tickets and y represent the number of student tickets sold. Which system of equations can be used to find how many of each ticket is sold?
Answers
Answer:
Adults = x
Students = y = x + 40. 40 more student than adult
Adult = $8, Student = $6
Total for Adults = 8*x = 8x
Total for students = 6*y = 6y
Total = $1920
8x + 6y = 1920
y = x + 40
8x + 6y = 1920
Step-by-step explanation:
Above
A circular rug has a radius of 3 ft. What is the circumference of the rug? Use 3.14 for Pi.9.32 ft
9.42 ft
18.64 ft
18.84 ft
Answers
Answer:
18.84 ft
Step-by-step explanation:
Circumference = 2pi*r = 6pi.
6*3.14 = 18.84
Answer:
18..84
Step-by-step explanation:
4.
Find the slope given the points (3,2) and (4,7).
a) 4
b) 5
c) -5
d) 1/5
I
Answers
Answer:
The slope would be 5, answer B.
You can find this by doing y2 - y1/ x2 - x1.
Hope this helps.
Step-by-step explanation:
more of my brothers wwork for yalll have fun and tysm!

Answers
3 x 12
= 36
Got 12 by reducing the numbers with the Greatest Common Factor (GCF) 4
Answer:
i cant wait to start are life together, with are son. im so thankful for u becca. ily
Step-by-step explanation:
The class president wants to survey the students at the high school about the selection of food offered by the school cafeteria. The president knows that there are 150 boys and 175
girls in the high school. Which of the following is a representative sample of the high school population?
A.Sample 4: 7 boys and 6 girls
B.Sample 1: 10 boys and 10 girl
C.Sample 2: 10 boys and 35 girls
D.Sample 3: 6 boys and 7 girls
Answers
Answer: C.Sample 2: 10 boys and 35 girls
Step-by-step explanation:
The class president wants to survey the students at the high school about the selection of food offered by the school cafeteria. The president knows that there are 150 boys and 175 girls.
girls in the high school. Which of the following is a representative sample of the high school population?
A.Sample 4: 7 boys and 6 girls
B.Sample 1: 10 boys and 10 girl
C.Sample 2: 10 boys and 35 girls
D.Sample 3: 6 boys and 7 girls
Sample 1: 10 boys and 10 girl. Therefore, option B is the correct answer.
What is random sampling?In statistics, a simple random sample is a subset of individuals chosen from a larger set in which a subset of individuals are chosen randomly, all with the same probability. It is a process of selecting a sample in a random way.
This is a representative sample of the high school population because it accurately reflects the ratio of boys to girls in the high school (150 boys and 175 girls). The sample has 10 boys and 10 girls, which is a 6.7:7.3 ratio, which is close to the 6.5:7.5 ratio in the overall high school population.
Therefore, option B is the correct answer.
Learn more about the random sample here:
https://brainly.com/question/12719656.
#SPJ2
The product of 9 and t squared, increased by the sum of the square of t anne 2
Answers
Answer:
10t2+ 2
Step-by-step explanation:
9t^{2} x (t^{2} + 2) add 9t2, and t2 to get 10t2 + 2
\(12+3v=27\)
Thanks!
Answers
Answer:
Solution given:
12+3v=27
3v=27-12
3v=15
v=\(\frac{15}{3}=5\)
v=5
12 + 3v = 27
⇛ 3x = 27 – 12
⇛ 3x = 15
⇛ x = 15/3
⇛ x = 5
Mary is at a mall observing people. She has observed 12 of the last 20 people were wearing boots. What is the experimental probability that the next person she see is NOT wearing boots?
Answers
Answer:
2/5
Step-by-step explanation:
P(boots) = 12/20
P(not boots) = 8/20 = 2/5
I will give you thanks and :)
Please help

Answers
Answer:
Scale factor = 2, x = 3 cm
Step-by-step explanation:
The scale factor is 2 because you can see that in the second figure you multiply the sides from the first one by 2.
Using the scale factor 2, you can multiply 1.5 * 2 = 3 for x.
If 2x + 3y = 15 and xy = 6, find 4x2 + 9y2
Need a quick help for my homework please help.
Answers
Answer:
2 (4x+9y)
Step-by-step explanation:
Simplified:
8x+18y
Find the exact value of sin 5pi/4
Answers
The exact value of sin 5π/4 is 0. 0677
How to find the value
It is important to note that π = 3. 142
Let's find sin 5π
Substitute the value
sin 5π = sin (5 × 3. 142) = sin 15. 71
= \(\frac{sin 15. 71}{4}\)
Find the sine of the number
= \(\frac{0. 27076}{4}\)
= \(0. 0677\)
Thus, the exact value of sin 5π/4 is 0. 0677
Learn more about trigonometric ratio here:
https://brainly.com/question/24349828
#SPJ1
Answer:
- sqrt2/2
Step-by-step explanation:
I got it wiring but I don’t know what I did wrong

Answers
Answer:
because the answer is 6.601 not 6.501
Step-by-step explanation:
you must have done the work wrong
WILL GIVE BRAINLESS IF YOU GOT IT CORRECT
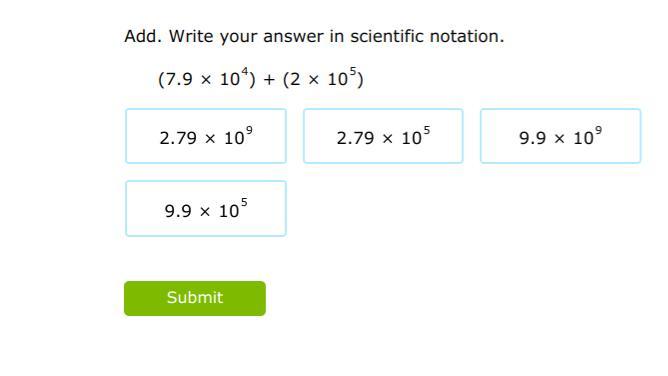
Answers
Answer: 2.79 x 10 to the 5th power
Step-by-step explanation: Your welcome :)
Answer:
2.79 x \(10^{5} }\)
Step-by-step explanation:
7.9 x \(10^{4}\) = 79000
2 x \(10^{5}\) = 200000
79000 + 200000 = 279000
279000 = 2.79 x \(10^{5} }\)
Hope this helps, I'm sorry about the earlier question but I fixed it:)
while logistic regression and classification and regression trees (cart) have the same end goal, each model approaches the goal in a different way. discuss the differences in the two models. provide a specific example of a situation where employing a cart model would be preferable to a logistic regression model. explain what makes the cart model superior in your example.
Answers
Logistic regression models the probability of a binary outcome, while CART models segment data into categories. For example, CART is preferable when data has complex interactions, as it can partition data into multiple categories.
Logistic regression and classification and regression trees (CART) are two different machine learning models used for binary classification problems. Logistic regression models the probability of one class or the other based on a linear combination of input variables. This makes it useful for predicting a binary outcome, such as whether a customer will purchase a product or not. On the other hand, CART is a decision tree model that divides data into categories. It uses a tree-like structure to split the data into segments based on the input features. This makes it useful for dealing with data with complex interactions, as it can partition data into multiple categories. For example, a CART model would be preferable to a logistic regression model if there are multiple underlying factors that affect the binary outcome. In this case, a CART model could more accurately identify the categories that are associated with a particular outcome. Overall, CART models are superior for dealing with data with complex interactions, whereas logistic regression is better for simpler data.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
A sphere has a Volume of 972 cubic feet. Find the radius of the sphere.
Answers
Answer:
6.15
Step-by-step explanation:
A gum manufacturer claims that on average the flavor of an entire packet of its gum would last for more than 39 minutes. A quality controller selects a random sample of 55 packets of gum. She finds the average time for which the gum flavor lasts is 40 minutes with a standard deviation of 5.67 minutes.
a) Formulate a hypothesis test to validate the manufacturer's claim.
b) After a new technique to improve the lasting period of gum flavor was applied, the quality controller reselects 60 packets of gum and found out that the average time for which the gum flavor lasts is 45 minutes with a standard deviation of 3.15 minutes. Is there sufficient evidence to conclude that the new technique significantly increased the lasting time?
c) Use a 95% confidence interval for the population average time for which the flavor lasts to validate the manufacturer's claim after the new technique is applied.
Answers
(a) A one-sample t-test was used to test a gum manufacturer's claim that the mean flavor time of a packet of gum is more than 39 minutes, and there was sufficient evidence to support the claim.
b) After a new technique was applied, a one-sample t-test was used to test whether the mean flavor time of a packet of gum is significantly higher than 39 minutes, and there was sufficient evidence to support the claim that the new technique increased the lasting time of the gum flavor.
c) A 95% confidence interval was calculated to validate the new population average time for which the flavor lasts after the new technique was applied, and the interval did not include 39 minutes, confirming the effectiveness of the new technique.
a) To test the manufacturer's claim, we can set up a hypothesis test,
Null hypothesis (H0): The mean flavor time of the 55 packets of gum is equal to 39 minutes.
Alternative hypothesis (Ha): The mean flavor time of the 55 packets of gum is greater than 39 minutes.
We can use a one-sample t-test to compare the mean flavor time of the sample to the manufacturer's claim.
The test statistic is calculated as:
t = (X - μ) / (s / √n)
where X is the sample mean,
μ is the population mean (in this case, 39 minutes),
s is the sample standard deviation,
And n is the sample size (55).
Using the information given in the problem,
We can calculate the test statistic as,
t = (40 - 39) / (5.67 / √55)
= 2.62
We can find the p-value associated with this test statistic using a t-distribution table.
For a one-tailed test with 54 degrees of freedom (55 - 1), the p-value is less than 0.01.
Since the p-value is less than the significance level of 0.05,
We reject the null hypothesis and conclude that there is sufficient evidence to support the claim that the mean flavor time of the 55 packets of gum is greater than 39 minutes.
b) To test whether the new technique significantly increased the lasting time, we can set up a hypothesis test:
Null hypothesis (H0): The mean flavor time of the 60 packets of gum is equal to 39 minutes.
Alternative hypothesis (Ha): The mean flavor time of the 60 packets of gum is greater than 39 minutes.
We can use a one-sample t-test again to compare the mean flavor time of the sample to the manufacturer's claim.
The test statistic is calculated as,
t = (X - μ) / (s / √n)
where X is the sample mean,
μ is the population mean (in this case, 39 minutes),
s is the sample standard deviation,
And n is the sample size (60).
Using the information given in the problem, we can calculate the test statistic as:
t = (45 - 39) / (3.15 / √60)
= 11.55
We can find the p-value associated with this test statistic using a t-distribution table.
For a one-tailed test with 59 degrees of freedom (60 - 1), the p-value is less than 0.00001.
Since the p-value is less than the significance level of 0.05, we reject the null hypothesis and conclude that there is sufficient evidence to support the claim that the new technique significantly increased the lasting time of the gum flavor.
(c) We can use the following formula to calculate the 95% confidence interval for the mean flavor time:
⇒ X± tα/2(s / √n)
where X is the sample mean (45 minutes),
s is the sample standard deviation (3.15 minutes),
n is the sample size (60),
And tα/2 is the t-value from the t-distribution with 59 degrees of freedom (corresponding to a 95% confidence level).
Using a t-distribution table,
we can find that t0.025,59 = 2.0027.
Plugging in the values, we get,
45 ± 2.0027(3.15 / √60)
This simplifies to,
(42.61, 47.39)
Therefore, we are 95% confident that the true population average time for which the flavor lasts after the new technique is applied is between 42.61 and 47.39 minutes.
Since this confidence interval does not include the manufacturer's claim of 39 minutes, we can conclude that the new technique did indeed significantly increase the lasting time of the gum flavor.
To learn more about statistics visit:
https://brainly.com/question/30765535
#SPJ4
what is 0.133 with a bar over 33
Answers
Answer:
2/15
Step-by-step explanation:
make x= 0.13
multiply it by 10^1 .
10x = − 1.33
subtract x from 10x
10x−x =
1.33 - 0.13
9x = 1.2
divide both sides by 9 to get x as a fraction
x = 1.2/9 =
12/90 =
2/15
httpssocraticorgquestionshowdoyouconvert0133beingrepeatedtoafraction#242780
A bar over a digit in a decimal number, such as 0.133 with a bar over the 3, indicates that the number is a repeating decimal. In this case, 0.133 is a repeating decimal and the digit 3 is repeating infinitely.
What is repeating decimal?A repeating decimal is a decimal number whose digits are periodic and repeat infinitely. They are also called recurring decimals. For example, 0.333... is a repeating decimal, with the digit 3 repeating indefinitely. The same goes for 0.666... and so on. They can also be represented in the form of a fraction, where the numerator is the repeating decimal and the denominator is a power of 10 with a 1 followed by as many zeroes as the number of digits in the repeating block. Repeating decimals can also be represented with a bar over the repeating block of digits, for example 0.133 with a bar over the 3, indicating that the digit 3 is repeating infinitely. It's also written as 0.133(3) where (3) means the repeating decimal. Another way is to use a dot above the repeating digit.To learn more about decimal refer:
brainly.com/question/703656
#SPJ1
2.1. Convert 15 cm to mm.
Answers
Answer:
150 mm
Step-by-step explanation:
To convert centimeters (cm) to millimeters (mm), you need to multiply the measurement by 10 since there are 10 millimeters in 1 centimeter.
1 cm = 10 mm
So, to convert 15 cm to mm:
15 cm * 10 = 150 mm
Therefore, 15 centimeters is equal to 150 millimeters.
Answer:
Step-by-step explanation:
1cm=10mm
15cm=150mm