it takes 7/4 yd of a ribbon to make a hair bow. how much ribbon is needed to make 9 bows
Answers
Answer:
15.75yd
Step-by-step explanation:
7/4 is 1.75
1.75x9 is 15.75
Related Questions
g a study based on the association primate ebmarah looked at the average age a baby gorilla leaves it's mother versus the average age a human baby leaves it's mother. naturally they are different, so we don't want a hypothesis test. instead, find an 86% confidence interval for the difference in age to leave mother.
Answers
An 86% confidence interval for the difference in age to leave mother is -3.10091
What is confidence Interval?
The mean of your estimate plus and minus the range of that estimate constitutes a confidence interval. Within a specific level of confidence, this is the range of values you anticipate your estimate to fall within if you repeat the test. In statistics, confidence is another word for probability.
Given, Gorilla Baby sample
x means x bar here so, \(x_{1}\) = 3.21
\(s_{1}\) = 0.81
\(n_{1}\) = 64
Human Baby sample
x means x bar here so, \(x_{2}\) = 19.1
\(s_{2}\) = 2.16
\(n_{2}\) = 200
Confidence interval needs t score
t score = 1.18
86% confidence interval = \(x_{1}\) - \(x_{2}\) ± tc \(\sqrt{s^{2} {1} / n_{2} + s^{2} {2} / n_{2}\)
= 3.21 - 19.1 ± 1.18 √0.81²/64 +2.16²/200
= 3.21 - 19.1 ± 1.18 √0.033
= -3.10091
An 86% confidence interval for the difference in age to leave mother is -3.10091
The detail question is here,
A study based on the Association primate Ebmarah looked at the average age a baby gorilla leaves it’s mother versus the average age the human baby leaves it’s mother . Naturally they are different , so we don’t want a hypothesis test. Instead, find an 86% confidence interval for the difference in age to leave mother.
Gorilla:
Sampled 64 babies
Stayed with mother on average 3.21 years
Standard deviation: 0.81
Human:
Sampled 200 babies
Stayed with mother on average 19.1 years
Standard deviation: 2.16
Matched pairs standard deviation :0.23
To learn more about confidence interval visit:
brainly.com/question/24131141
#SPJ4
Determine whether it is a function

Answers
Answer:
Relation 1: FunctionRelation 2: FunctionStep-by-step explanation:
A function is defined so that for each input, there is no more than one output.
How can u find a geometry-big circle mAB=56 mBC=59 mCD=63 mDE=63 mEF= 31
Answers
To find the measure of the geometry-big circle, we need to sum up the measures of all the arcs around the circle.
We are given the following measures:
\(\sf\:m\angle AB = 56 \\\)
\(\sf\:m\angle BC = 59 \\\)
\(\sf\:m\angle CD = 63 \\\)
\(\sf\:m\angle DE = 63 \\\)
\(\sf\:m\angle EF = 31 \\\)
To find the measure of the geometry-big circle, we add up these measures:
\(\sf\:m\angle AB + m\angle BC + m\angle CD + m\angle DE + m\angle EF \\\)
Substituting the given values:
\(\sf\:56 + 59 + 63 + 63 + 31 \\\)
Simplifying the expression:
\(\sf\:272 \\\)
Therefore, the measure of the geometry-big circle is 272.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\textcolor{red}{\underline{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
2. AB = 3x + 2
AD = x +39
Answers
Answer:
x=18.5
u gotta do 3x+2=x+49
combine the like terms and it becomes 2x=37 then divide by 2 u get 18.5
plug it in as x and check if it's right
find the mean of the distribution

Answers
Answer:
yyy
Step-by-step explanation:
Answer:Canst see
Step-by-step explanation:
sorry my guy
Jada went to the mall yesterday with $30.
• She spent 2/5 of her money on a new purse.
She spent / of what was left at the food court.
• She gave $5 to her friend.
How much did she have left?
Answers
which of these is most likely to weigh 2 kilograms car roast chicken horse egg tea bag
Answers
The item most likely to weigh 2 kilograms is a roast chicken.
Which of them would weight 2 kilograms?
The size, breed, and any other ingredients or stuffing used can all affect the weight of a roast chicken. Weights of roast chickens can range from petite ones weighing less than 1 kilogram to larger ones weighing more than 2 kilograms.
The other things that we have there would either weigh less than 2 Kg such as a tea bag or much more than 2 Kg such as a horse. The egg and the tea a very light and would be less than 2 Kg in weight while the bag and the horse would be above 2 Kg in weight.
Learn more about weight:https://brainly.com/question/31659519
#SPJ1
Suppose a company's revenue function is given by R(q) = - q^3 + 220q^2 and its cost function is given by C(q) = 500 + 13q, where q is hundreds of units sold/produced, while R(q) and C(q) are in total dollars of revenue and cost, respectively.
A) Find a simplified expression for the marginal profit function. (Be sure to use the proper variable in your answer.)
MP(q) =
B) How many items (in hundreds) need to be sold to maximize profits? (Round your answer to two decimal places.)
Answers
Answer:
A) MP(q) = -3q² + 440q - 13
B) 146.64 units.
Step-by-step explanation:
The profit function is given by the revenue minus the cost function:
\(P(q) = R(q) - C(q)\\P(q) = -q^3+220q^2-500-13q\)
A) The Marginal profit function is the derivate of the profit function as a function of the quantity sold:
\(P(q) = -q^3+220q^2-500-13q\\MP(q) = \frac{dP(q)}{dq} \\MP(q)=-3q^2+440q-13\)
B) The value of "q" for which the marginal profit function is zero is the number of items (in hundreds) that maximizes profit:
\(MP(q)=0=-3q^2+440q-13\\q=\frac{-440\pm \sqrt{440^2-(4*(-3)*(-13))} }{-6}\\q'=146.64\\q'' = - 0.03\)
Therefore, the only reasonable answer is that 146.64 hundred units must be sold in order to maximize profit.
solve this equation -1/2 ( -3y + 10)
Answers
Answer:
3/2y-5
Step-by-step explanation:
Determine la ecuación de la recta normal a la curva f(x)=ax(bx+a) en el punto de abscisa x=1. Dar como respuesta el intercepto al Eje Y . Considere el valor de a=7 ,b=10
Answers
Answer:
\(f(x) = ax(bx + a) \\ a = 1 \: b = 10 \: x = 1 \\ f(x) = ax(bx + a) \\ f(1) = 7(1)(10(1) + 7) \\ f(1)= 7(10 + 7) \\ f(1)= 70 + 49 \\ f(1)= 149\)
What is the smallest positive integer $n$ such that $\sqrt[4]{56 \cdot n}$ is an integer?
Answers
The smallest positive integer n such that t \($\sqrt[4]{56 \cdot n}$\) is an integer is 686.
We have to find the smallest positive integer n such that \($\sqrt[4]{56 \cdot n}$\) is an integer
To find the smallest positive integer n such that \($\sqrt[4]{56 \cdot n}$\) is an integer, we need to determine the factors of 56 and find the smallest value of n that, when multiplied by 56, results in a perfect fourth power.
The prime factorization of 56 is:
56 = 2³ × 7
The prime factors of 56 need to be raised to multiples of 4.
Therefore, we need to determine the smallest value of n that includes additional factors of 2 and 7.
To make the expression a perfect fourth power, we need to raise 2 and 7 to the power of 4, which is 2⁴ × 7⁴
The smallest value of n that satisfies this condition is:
n = 2 × 7³ = 2× 343 = 686
To learn more on Integers click:
https://brainly.com/question/490943
#SPJ1
you sailed 0.032 units to the left and found treasure at 0.248 units find where the ship started
Answers
Are the vectors 2+5x+3x2, 4+11x+6x2 and 1+2x+x2 linearly independent? choose If the vectors are independent, enter zero in every answer blank since zeros are only the values that make the equation below true. If they are dependent, find numbers, not all zero, that make the equation below true. You should be able to explain and justify your answer. 0= (2+5x+3x2)+ (4+11x+6x2)+ (1+2x+x2).
Answers
Answer:
Vectors \(p_{1} = 2+5\cdot x + 3\cdot x^{2}\), \(p_{2} = 4+11\cdot x +6\cdot x^{2}\) and \(p_{3} = 1+2\cdot x +x^{2}\) are linearly independent.
Step-by-step explanation:
From Linear Algebra, we must remember that a set of vectors is linearly independent if and only if coefficients of its linear combinations are all zeroes. That is:
\(\Sigma\limits_{i=1}^{n} \alpha_{i}\cdot p_{i}= 0\), where \(\alpha_{i} = 0\). (Eq. 1)
Where:
\(p_{i}\) - i-th Polynomial of the set of vectors, dimensionless.
\(\alpha_{i}\) - i-th coefficient associated with the i-ith polynomial of the set of vectors, dimensionless.
Let \(p_{1} = 2+5\cdot x + 3\cdot x^{2}\), \(p_{2} = 4+11\cdot x +6\cdot x^{2}\) and \(p_{3} = 1+2\cdot x +x^{2}\) elements of the set of vectors, whose linear combination is:
\(\alpha_{1}\cdot p_{1}+\alpha_{2}\cdot p_{2}+\alpha_{3}\cdot p_{3}= 0\)
\(\alpha_{1}\cdot (2+5\cdot x+3\cdot x^{2})+\alpha_{2}\cdot (4+11\cdot x +6\cdot x^{2})+\alpha_{3}\cdot (1+2\cdot x+x^{2}) = 0\)
\((2\cdot \alpha_{1}+4\cdot \alpha_{2}+\alpha_{3})+(5\cdot \alpha_{1}+11\cdot \alpha_{2}+2\cdot \alpha_{3})\cdot x+(3\cdot \alpha_{1}+6\cdot \alpha_{2}+\alpha_{3})\cdot x^{2} = 0\)
Values of coefficient are contained in the following homogeneous system of linear equations:
\(2\cdot \alpha_{1}+4\cdot \alpha_{2}+\alpha_{3} = 0\) (Eq. 2)
\(5\cdot \alpha_{1}+11\cdot \alpha_{2}+2\cdot \alpha_{3} = 0\) (Eq. 3)
\(3\cdot \alpha_{1}+6\cdot \alpha_{2}+\alpha_{3} = 0\) (Eq. 4)
The solution of this system is:
\(\alpha_{1} = 0\), \(\alpha_{2} = 0\), \(\alpha_{3} = 0\)
Which means that given set of vectors are linearly independent.
What is the sine of 0?
(Need help)

Answers
The angle of sinθ between the horizontal vector (1, 0) and the slant vector (15/17, -8/17) is sin⁻¹(8/17), which is approximately 29.11 degrees.
To find the angle of sinθ between a horizontal vector and a slant vector, we can use the dot product formula:
a · b = |a| |b| cos(θ)
where a and b are vectors, |a| and |b| are their magnitudes, and theta is the angle between them.
In this case, the horizontal vector is (1, 0) and the slant vector is (15/17, -8/17).
The magnitude of the horizontal vector is 1, and the magnitude of the slant vector is:
|b| = sqrt((15/17)² + (-8/17)²) = sqrt(225/289 + 64/289) = sqrt(289/289) = 1
The dot product of the two vectors is:
a · b = (1)(15/17) + (0)(-8/17) = 15/17
So we have:
15/17 = (1)(1) cos(θ)
cos(θ) = 15/17
To find sin(θ), we can use the trigonometric identity:
sin²(θ) + cos²(θ) = 1
sin²(θ) = 1 - cos²(θ) = 1 - (15/17)² = 64/289
Taking the square root of both sides, we get:
sin(theta) = sqrt(64/289) = 8/17
To learn more about the vectors;
brainly.com/question/13188123
#SPJ1
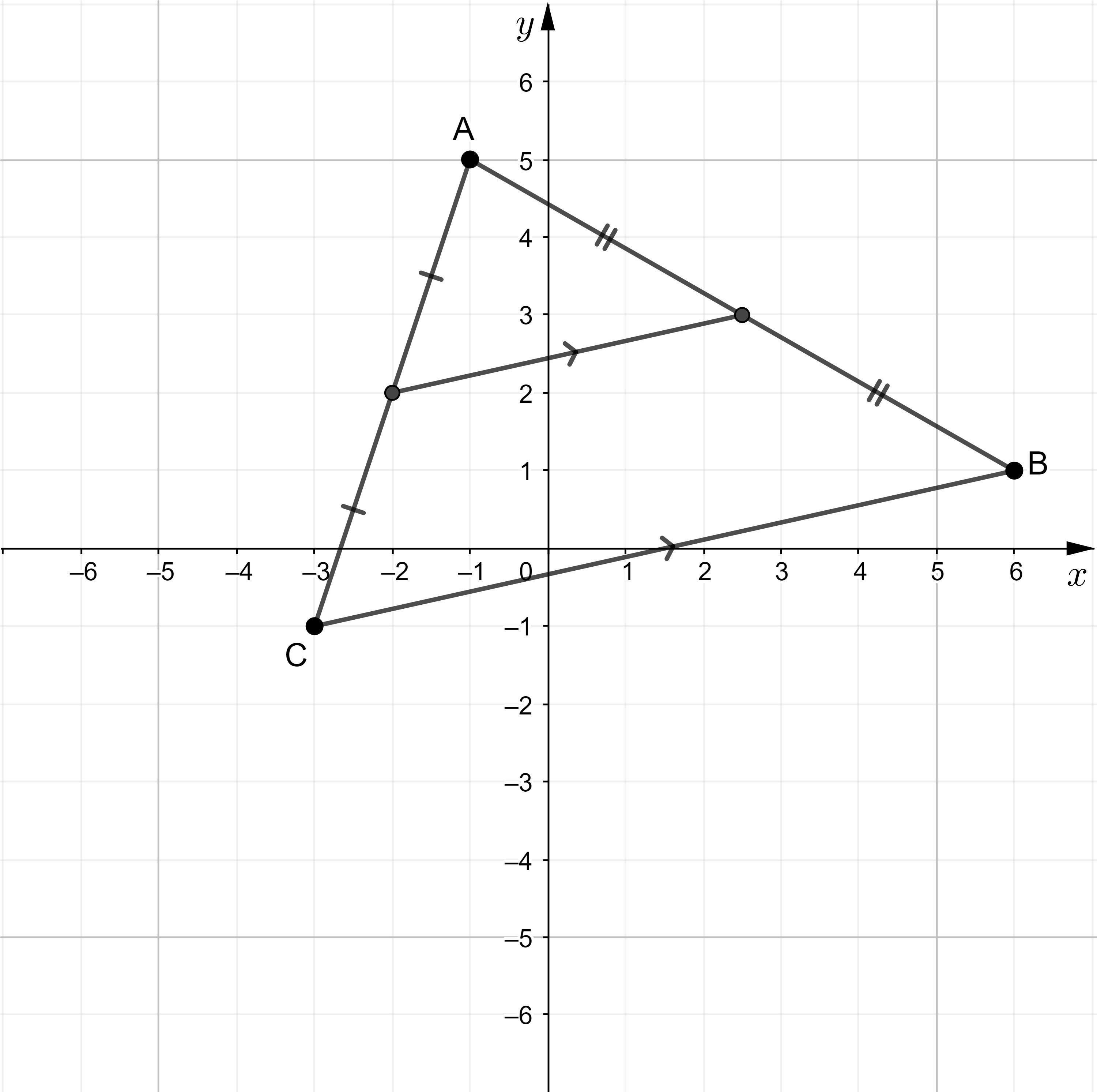
NO LINKS!! URGENT HELP PLEASE!!
Please help me with #20

Answers
Answer:
\(\text{Midpoint of $AC$}=\left(-2,2\right)\)
\(\text{Midpoint of $AB$}=\left(\dfrac{5}{2},3\right)\)
\(\text{Slope of midsegment}=\dfrac{2}{9}\)
\(\text{Slope of $AC$}=3\)
\(\text{Slope of $BC$}=\dfrac{2}{9}\)
\(\text{Length of midsegment}=\dfrac{\sqrt{85}}2\)
\(\text{Length of $BC$}=\sqrt{85}\)
Step-by-step explanation:
Given points:
A = (-1, 5)B = (6, 1)C = (-3, -1)To determine the midpoints of AC and AB, substitute the given points into the midpoint formula.
\(\boxed{\begin{minipage}{7.4 cm}\underline{Midpoint between two points}\\\\Midpoint $=\left(\dfrac{x_2+x_1}{2},\dfrac{y_2+y_1}{2}\right)$\\\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the endpoints.\\\end{minipage}}\)
\(\begin{aligned}\text{Midpoint of $AC$}&=\left(\dfrac{x_C+x_A}{2},\dfrac{y_C+y_A}{2}\right)\\\\&=\left(\dfrac{-3-1}{2},\dfrac{-1+5}{2}\right)\\\\&=\left(\dfrac{-4}{2},\dfrac{4}{2}\right)\\\\&=\left(-2,2\right)\end{aligned}\)
\(\begin{aligned}\text{Midpoint of $AB$}&=\left(\dfrac{x_B+x_A}{2},\dfrac{y_B+y_A}{2}\right)\\\\&=\left(\dfrac{6-1}{2},\dfrac{1+5}{2}\right)\\\\&=\left(\dfrac{5}{2},\dfrac{6}{2}\right)\\\\&=\left(\dfrac{5}{2},3\right)\end{aligned}\)
\(\hrulefill\)
\(\boxed{\begin{minipage}{8cm}\underline{Slope Formula}\\\\Slope $(m)=\dfrac{y_2-y_1}{x_2-x_1}$\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are two points on the line.\\\end{minipage}}\)
To determine the slope of the midsegment, substitute the midpoints of AC and AB into the slope formula:
\(\begin{aligned}\text{Slope of midsegment}&=\dfrac{y_{AB}-y_{AC}}{x_{AB}-x_{AC}}\\\\&=\dfrac{2-3}{-2-\frac{5}{2}}\\\\&=\dfrac{-1}{-\frac{9}{2}}\\\\&=\dfrac{2}{9}\end{aligned}\)
Therefore, the slope of the midsegment is 2/9.
To find the slope of AC, substitute the points A and C into the slope formula:
\(\begin{aligned}\text{Slope of $AC$}&=\dfrac{y_{C}-y_{A}}{x_{C}-x_{A}}\\\\&=\dfrac{-1-5}{-3-(-1)}\\\\&=\dfrac{-6}{-2}\\\\&=3\end{aligned}\)
Therefore, the slope of the AC is 3.
**Note** There may be an error in the question. I think you are supposed to find the slope of BC (not AC) since there is no relationship between the slopes of the midsegment and AC, but there is a relationship between the slopes of the midsegment and BC.
\(\begin{aligned}\text{Slope of $BC$}&=\dfrac{y_{C}-y_{B}}{x_{C}-x_{B}}\\\\&=\dfrac{-1-1}{-3-6}\\\\&=\dfrac{-2}{-9}\\\\&=\dfrac{2}{9}\end{aligned}\)
The slope of BC is 2/9, so the slopes of the midsegment and BC are the same. This implies that the midsegment and BC are parallel.
\(\hrulefill\)
\(\boxed{\begin{minipage}{7.4 cm}\underline{Distance Formula}\\\\$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$\\\\\\where:\\ \phantom{ww}$\bullet$ $d$ is the distance between two points. \\\phantom{ww}$\bullet$ $(x_1,y_1)$ and $(x_2,y_2)$ are the two points.\\\end{minipage}}\)
To find the length of the midsegment, substitute the endpoints (-2, 2) and (5/2, 3) into the distance formula:
\(\begin{aligned}\text{Length of midsegment}&=\sqrt{\left(\frac{5}{2}-(-2)\right)^2+(3-2)^2}\\\\&=\sqrt{\left(\frac{9}{2}\right)^2+(1)^2}\\\\&=\sqrt{\frac{81}{4}+1}\\\\&=\sqrt{\frac{85}{4}}\\\\&=\dfrac{\sqrt{85}}2\end{aligned}\)
To find the length of the BC, substitute points B and C into the distance formula:
\(\begin{aligned}\text{Length of $BC$}&=\sqrt{(x_C-x_B)^2+(y_C-y_B)^2}\\&=\sqrt{(-3-6)^2+(-1-1)^2}\\&=\sqrt{(-9)^2+(-2)^2}\\&=\sqrt{81+4}\\&=\sqrt{85}\end{aligned}\)
Therefore, the length of BC is twice the length of the midsegment.
Can anyone give an explanation and answer? (Algebra 1)

Answers
Answer:
256x^2
Step-by-step explanation:
The square root of (16x)^4 is (16x)^2 because you divide the power by root and 16x squared is equal to 256x^2
Answer:
256x²
Step-by-step explanation:
Simplify the radical by breaking the radicand up into a product of known factors, assuming positive real numbers.
Robert had 2 2/5 cups of chocolate syrup left in his freezer he used 1/4 cup of Chocolate syrup when he makes a milkshake what is the maximum number of milkshakes that Robert can make with the chocolate syrup

Answers
Robert can make a maximum of 8 milkshakes with the remaining chocolate syrup.
How to find the maximum number of milkshakes that Robert can make with the chocolate syrupConverting the mixed number 2 2/5 to an improper fraction: 2 2/5 = 12/5
Subtracting the amount of chocolate syrup used per milkshake from the total amount of chocolate syrup:
12/5 - 1/4 = (48 - 5) / 20 = 43/20
Therefore, Robert has 43/20 cups of chocolate syrup left, which is the maximum amount he can use to make milkshakes.
For maximum number of milkshakes:
(43/20) / (1/4) = (43/20) x (4/1) = 172/20 = 8.6
Since Robert cannot make a fraction of a milkshake, he can make a maximum of 8 milkshakes with the remaining chocolate syrup.
Learn more about word problems at https://brainly.com/question/21405634
#SPJ1
A projectile is fired straight up from ground level. After t seconds, its height above the ground is s feet, where s= - 16t² + 128t
For what time period is the projectile at least 192 feet above the ground?
Select the correct choice below and fill in the answer boxes to complete your choice.
OA. For the time period between (and inclusive of)
(Simplify your answers.)
OB. For the time period between (and not inclusive of)
(Simplify your answers.)
seconds and
seconds and
seconds the projectile will be at least 192 ft above the ground.
seconds the projectile will be at least 192 ft above the ground.
Answers
For the time period of the projectile at least 192 feet above the ground is between 2 second and 6 second
Since s=128t-16t2, we want to know the 2 times where 128t-16t2=192, as those two values will be the begin and end times of the interval in question. We can rewrite that equation in standard quadratic equation form:
16t2-128t+192=0 or, simplified, 8t2-64t+96=0
or t2-8t+12=0
since it is now in quadratic form, we can solve using the quadratic formula:
t = 2 and 6
So the time period from approximately 2 second and 6 second has the projectile above 192 feet.
Learn more about projectile here:
https://brainly.com/question/1659208
#SPJ9
Which expression represents that an unknown number x is no less than 6?
x < 6
x > 6
x ≤ 6
x ≥ 6
Answers
Answer:
x≥ 6
Step-by-step explanation:
hope this helps loves x please make me brainlest
Answer: your answer would be D. x ≥ 6
x is greater or equal to 6
Step-by-step explanation:
I need help with this problem

Answers
Part (a)
\(g(x)=-3x^2 - 12x-11 \\ \\ =-3(x^2 + 4x)-11 \\ \\ =-3(x^2+4x+4)-11+12 \\ \\ =\boxed{-3(x+2)^2+1}\)
So, the vertex is at (-2, 1).
Part (b)
Plot the vertex, (-2,1).
Also, when x = -3, g(x) = -3(-1)² + 1 = -2. Since the graph is symmetric about x = -2, plot (-3, -2) and (-1, -2).
By similar logic, you can also plot (-4, -11) and (0, -11).

Bob has a total of 60 adventure cards for a game. The table shows the number of cards, c, distributed to p players. Which equation describes the
paltem in the table?
Does anyone know the answer for this ?

Answers
Answer:
A. c = 60 / p
Step-by-step explanation:
If p=2, the equation would read... c = 60 / 2, which mean c = 30. If c = 12, the equation would read... 12 = 60 / p, and p = 5, and so on, 20 = 60 / 3, and 15 = 60 / 4.
Please help me with the following question.

Answers
Answer:
Step-by-step explanation:
The probability Mrs. Walker will pick all 32 of the first round games correctly is given by:
0.56^32 = 1.56789e-10
To find the probability that Mrs. Walker will pick exactly 8 games correctly in the first round, we can use the binomial formula:
P(x=8) = 32 choose 8 * 0.56^8 * (1-0.56)^(32-8)
Where 32 choose 8 is the number of ways to choose 8 games out of 32.
To find the probability that Mrs. Walker will pick exactly 28 games incorrectly in the first round, we can use the same formula as in 2:
P(x=4) = 32 choose 4 * 0.56^4 * (1-0.56)^(32-4)
Ariana is baking chocolate chip cookies for a bake sale. For every 3 cups of flour, she needs 2 cups of sugar. How many cups of sugar will she need if she has measured 18 cups of flouf?
Answers
since she already has 18 cups flour she needs 6 cups of sugar
Diameter of the tin on the picture = ? Height of the tin on the picture = ? Actual weight of coffee = 750 g 1.1 Measure the diameter of the tin in mm and write down the real diameter in mm 1.2 Hence, determine the circumference of the base of the tin in mm. You may us the formula: CС = 2πr Hint: radius = half of diameter MATHEMATICAL LITERACY GRADE 11, 2023 SBA GUIDELINE π = 3,142 Page 2 (3) (3)
Answers
We can write the diameter and circumferance of base as -
D = 2√(750ρ/πh)
C = 2π√(750ρ/πh)
What is function?A function is a relation between a dependent and independent variable.
Mathematically, we can write → y = f(x) = ax + b.
Given is to find the diameter and height of the tin can.
Assume the density of coffee as {ρ}. We can write the volume of the tin can as -
Volume = mass x density
Volume = 750ρ
We can write -
πr²h = 750ρ
r = √(750ρ/πh)
D = 2r
D = 2√(750ρ/πh)
Now, we can write the circumferance as -
C = 2πr
C = 2π√(750ρ/πh)
Therefore, we can write the diameter and circumferance of base as -
D = 2√(750ρ/πh)
C = 2π√(750ρ/πh)
To solve more questions on cylinder, visit the link-
brainly.com/question/29014197
#SPJ2
the 7th-grade class wants to collect empty soda pop cans to earn $50.00. If pop cans earn $0.25 per pound how many cans will they need to collect to earn the $50.00?
Answers
200 pounds need to collect to earn the $50.00. Divide the cost per pound from the total amount needed, \(\frac{50.00}{0.25}\)= 200 pounds.
Is the British pound?The official money of the U.k. and its regions is the GBP, or British pound sterling. The Pound is the earliest currency that is still accepted as legal tender in the entire world. The GBP, represented by pound sign (£), has one of the greatest trade volumes worldwide.
What makes something a "pound"?The development of the pounds sterling -The Latin word "libra," which means balance and weight, is where the name "pound sterling" comes from. During the years, the pound banknotes underwent various revisions before being initially printed by the Bank of England and over 300 years ago.
To know more about pound visit:
https://brainly.com/question/29181271
#SPJ1
3/4 + 1/2 times 2 please help thanks
Answers
Answer:
7/4
Step-by-step explanation:
1/2 x 2 = 1
3/4 + 1 = 7/4 or 1 3/4
4x + 5 + 5x + 6 = 29. Whats X?
Answers
Answer:
9x
Step-by-step explanation:
the full answer is 9x+11=29
Answer:
X=2
Step-by-step explanation:
Add the numbers
4+5+5+6=29
4x+{\color{#c92786}{5}}+5x+{\color{#c92786}{6}}=29
4x+5+5x+6=294+11+5=29
4x+{\color{#c92786}{11}}+5x=29
4x+11+5x=29
Combine like terms
Subtract
1
1
11
11
from both sides of the equation
Simplify
Divide both sides of the equation by the same term
Simplify
Solution
=
2
solve and represent on a graph x+4≥10x-23
Answers
Three blocks are shown: Block A has mass 3 kilograms, length 8 centimeters, height 2 centimeters, and width 1 centimeters. Block B has mass 4 kilograms, length 1 centimeters, height 8 centimeters, and width 2 centimeters. Block C has mass 4 kilograms, length 8 centimeters, height 1 centimeters, and width 2 centimeters. Which statement is correct? (1 point) a Block A has the greatest density. b Block B has the least density. c The density of Block A is equal to the density of Block B. d The density of Block B is equal to the density of Block C.
Answers
Answer:
b & c
Step-by-step explanation:
Part A: Explain why the x-coordinates of the points where the graphs of the equations y = 8^x and y = 2^x + 2 intersect are the solutions of the equation 8^x = 2^x + 2. (4 points)
Part B: Make tables to find the solution to 8^x = 2^x + 2. Take the integer values of x between −3 and 3. (4 points)
Part C: How can you solve the equation 8^x = 2^x + 2 graphically? (2 points)
Answers
Answer + Step-by-step explanation:
Part A :
Let M(a , b) be a point where the graphs
of the equations y = 8ˣ and y = 2ˣ⁺² intersect.
M lies on both graphs
Then
the coordinates of M verify both equations (equation of graph1 and equation of graph 2)
Then
\(b=8^{a}\ \text{on the other hand} \ b=2^{a+2}\)
Then
\(8^{a}=2^{a+2}\)
Therefore ‘a’ (the x-coordinates of the points M where the two graphs intersect) is a solution to the equation :
\(8^{x}=2^{x+2}\)
Part B : check the attached table.
Part C :
Graphically, we try to spot the points of intersection of the two graphs ,the x-coordinates of those points are the solution to our equation.
In our case , obviously the two graphs intersect at only one point M(1 ,8)
Therefore 1 is the only solution to 8ˣ = 2ˣ⁺².
Also ,Check the attached graph.

