Is the following situation proportional? Justify your answer. At an arcade, Aisha pays $2 for each game she plays.
Answers
Yes, the situation as described is proportional.
Discussion:
According to the question:
We are required to determine if the situation described in the question is proportional.Since, Aisha pays $2 for each game she plays at the arcade.
In essence, the total amount of money paid by Aisha will depend on the number of games she plays. On this note, the situation is proportional.
Read more on proportional:
https://brainly.com/question/3202565
Related Questions
100 POINTS PEOPLE!!!!!
Answers
Answer: Poggers, what if i did 2000 points???
Step-by-step explanation:
Answer:
lol
Step-by-step explanation:
How many license plates can be made using either 3 letters followed by 3 digits or 4 letters followed by 2 digits?
Answers
There can be a total of 63,273,600 license plates that can be made using either 3 letters followed by 3 digits or 4 letters followed by 2 digits.
To determine the number of license plates that can be made using either 3 letters followed by 3 digits or 4 letters followed by 2 digits, we need to calculate the total number of possibilities for each case and then sum them up.
3 letters followed by 3 digits
There are 26 letters in the English alphabet (assuming we're considering only uppercase letters), and 10 digits (0-9). In this case, we have 26 choices for each of the three letters and 10 choices for each of the three digits. Therefore, the number of license plates in this case is:
26 * 26 * 26 * 10 * 10 * 10 = 17,576,000
4 letters followed by 2 digits
Similar to Case 1, we have 26 choices for each of the four letters and 10 choices for each of the two digits. Therefore, the number of license plates in this case is:
26 * 26 * 26 * 26 * 10 * 10 = 45,697,600
To find the total number of license plates, we add the results from both cases:
17,576,000 + 45,697,600 = 63,273,600
Therefore, there can be a total of 63,273,600 license plates that can be made using either 3 letters followed by 3 digits or 4 letters followed by 2 digits.
Learn more about digits here:
https://brainly.com/question/30142622
#SPJ11
The quadratic equation x x4 3 2 0 2 − − = has what roots
Answers
The quadratic equation x2 - 4x + 3 = 0 has two roots. The roots are given by the quadratic formula as x = [4 ± √(16 - 12)]/2, which gives x = [4 ± 2√3]/2. Therefore, the roots are x = 2 ± √3.
The quadratic equation x^2 - 4x - 3 = 0 has two roots.
To find the roots of this equation, we can use the quadratic formula:
x = (-b ± √(b^2 - 4ac))/(2a)
In this case, a = 1, b = -4, and c = -3. Plugging these values into the quadratic formula, we get:
x = (-(-4) ± √((-4)^2 - 4(1)(-3)))/(2(1))
x = (4 ± √(16 + 12))/2
x = (4 ± √28)/2
x = (4 ± 2√7)/2
Simplifying further, we get:
x = 2 ± √7
Therefore, the two roots of the equation are x = 2 + √7 and x = 2 - √7.
Learn more about quadratic equation here: brainly.com/question/24349828
#SPJ11
Joy is helping her father to build a rectangular deck that measures 14 ft by 19 ft.
Find the area of the deck.
Answers
The answer is 126ft
Solve 5x - 9 = 2x + 3
Answers
Answer:
x=4
Step-by-step explanation:
Simplifying
5x + 9 = 2x + -3
Reorder the terms:
9 + 5x = 2x + -3
Reorder the terms:
9 + 5x = -3 + 2x
Solving
9 + 5x = -3 + 2x
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-2x' to each side of the equation.
9 + 5x + -2x = -3 + 2x + -2x
Combine like terms: 5x + -2x = 3x
9 + 3x = -3 + 2x + -2x
Combine like terms: 2x + -2x = 0
9 + 3x = -3 + 0
9 + 3x = -3
Add '-9' to each side of the equation.
9 + -9 + 3x = -3 + -9
Combine like terms: 9 + -9 = 0
0 + 3x = -3 + -9
3x = -3 + -9
Combine like terms: -3 + -9 = -12
3x = -12
Divide each side by '3'.
x = -4
Simplifying
x = -4
Hope this helps :)
find the change in volume dv if the radius of a sphere changes from 18 cm to 18.3 cm.
Answers
The change in volume (dv) is equal to 1221.45 cm³ if the radius of the sphere changes from 18 cm to 18.3 cm.
The change in the volume of the sphere can be represented by the following formula;
dV = 4πr²(dr)
Here dV is the change in the volume, r represents the radius and dr represents the change in the radius of the sphere.
As the radius of this sphere changes from 18 cm to 18.3 cm, we first calculate the change in radius by subtraction;
change in radius = 18.3 - 18 = 0.3 cm
Now substituting the values in the equation;
dV = 4π(18²)(0.3)
dV = 4π(324)(0.3)
dV = 4π(97.2)
dV = 1221.45
Therefore, the change in the volume of the sphere is 1221.45 cm³
To learn more about change in volume, click here:
https://brainly.com/question/13128572
#SPJ4
Acellus
The translation of ABCD to A'B'C'D'
is given by (x+[?],y-[ ]).
5
4
B
С
3
2
А
В'
C'
-7
-6 -5
-4
-3
-2
0
1
2.
3
4
5
A1
A
D
Enter
![AcellusThe translation of ABCD to A'B'C'D'is given by (x+[?],y-[ ]).54B32'C'-7-6 -5-4-3-2012.345A1ADEnter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/zyTiUAbzn8UvVDp3r05Q3aTf0g7cuTFv.png)
Answers
Answer:
Step-by-step explanation:
its (x+1,y+-3)
graphing linear equation.5x-9y=-7
Answers
The graph of the linear equation, 5x - 9y = -7, is in the attachment below.
How to Graph a Linear Equation?The linear equation that models a graph can be written in slope-intercept equation as y = mx + b. The value of the slope, which is the rise over the run of the line is represented as m, while the value of b, which is where the line intercepts the y-axis is b.
Given the linear equation, 5x - 9y = -7, rewrite in slope-intercept form:
5x - 9y = -7
-9y = -5x - 7
-9y/-9 = -5x/-9 - 7/-9
y = 5/9x + 7/9
This means the rise over the run of the line, m is 5/9, while the y-intercept of the graph, b is 7/9.
The graph is shown below.
Learn more about the graph of linear equation on:
https://brainly.com/question/4074386
#SPJ1

what’s the area and perimeter

Answers
The perimeter is 12
Hope this helps.
Good luck!
M and N are similar shapes. Work out the missing lengths, x and y.
HELP

Answers
Step-by-step explanation:
x=3.8 y=6 is your answer right answer
according to government data, 51% of employed women have never been married. rounding to 4 decimal places, if 15 employed women are randomly selected: a. what is the probability that exactly 2 of them have never been married? b. that at most 2 of them have never been married? c. that at least 13 of them have been married?
Answers
a) The probability that exactly 2 of them have never been married is\(0.0026 \text{ or }2.6*10^{-3}\)
b) The probability that at most 2 of them have never been married is\(0.0029\text{ or }2.9*10^{-3}\)
c) The probability that at least 13 of them have been married is \(0.0046 \text{ or } 4.6*10^{-3}\)
a) What is the probability that exactly 2 of them have never been married?
By applying binomial probability distribution method,
\(P(x)=^{n}C_{x}p^{x}q^{n-x}\)
Substitute,
P(x) =Binomial probability = 51% = 0.51
x = No. of times of an outcome = 2
n = No. of trials = 15
q = Probability of failure = 49% = 0.49
\(^{n}C_{x}\) = No. of combinations
\(P(2)=^{15}C_{2}*(0.51)^{2}*(0.49)^{15-2}\\\\P(2)=\frac{15!}{13!2!} *(0.51)^{2}*(0.49)^{13}\\\\P(2)=0.0026 \text{ or }2.6*10^{-3}\)
b) What is the probability that at most 2 of them have never been married?
By applying binomial probability distribution method,
\(P(x)=^{n}C_{x}p^{x}q^{n-x}\)
Substitute,
P(x) =Binomial probability = 51% = 0.51
x = No. of times of an outcome = 0,1,2
n = No. of trials = 15
q = Probability of failure = 49% = 0.49
\(^{n}C_{x}\) = No. of combinations
\(P(0-2)=^{15}C_{0}*(0.51)^{0}*(0.49)^{15-0}+^{15}C_{1}*(0.51)^{1}*(0.49)^{15-1}+^{15}C_{2}*(0.51)^{2}*(0.49)^{15-2}\\\\P(0-2) = 2.253*10^{-5}+15*0.51*4.59987*10^{-5}+2.563*10^{-3}\\\\P(0-2)=0.0029 \text{ or }2.9*10^{-3}\)
c)What is the probability that at least 13 of them have been married?
By applying binomial probability distribution method,
\(P(x)=^{n}C_{x}p^{x}q^{n-x}\)
Substitute,
P(x) =Binomial probability = 51% = 0.51
x = No. of times of an outcome = 13,14,15
n = No. of trials = 15
q = Probability of failure = 49% = 0.49
\(^{n}C_{x}\) = No. of combinations
\(P(13-15)=^{15}C_{13}*(0.51)^{13}*(0.49)^{15-13}+^{15}C_{14}*(0.51)^{14}*(0.49)^{15-14}+^{15}C_{15}*(0.51)^{15}*(0.49)^{15-15}\\\\P(13-15)= 105*(0.51)^{13}*(0.49)^{2}+15* (0.51)^{14}*(0.49)+(0.51)^{15}\\\\P(13-15)= 0.0046 \text{ or } 4.6*10^{-3}\)
To learn more about binomial probability distribution, refer:
https://brainly.com/question/15246027
#SPJ4
Please help
Dion bought tickets for Fun Park so that he and his friends would each have the same number of tickets. There are enough tickets so that each person can
ride the go-carts once, play video games three times, and play laser tag twice.
When Dion purchased the tickets for himself and his eight friends, he realized
that he could purchase ticket books, individual tickets, or a combination of
books and individual tickets. Dion figured out the cheapest way to buy tickets for his
group. What was the cheapest way and what was the total cost?
Answers
Answer:
25
Step-by-step explanation:
angles a and b are supplementary .if angle a is X and ange b is x-10 .find the measure of of both angles
Answers
Answer:
Angle A is 95 degrees and Angle B is 85 degrees.
Step-by-step explanation:
Since angles a and b are supplementary, their measures add up to 180 degrees.
Let's set up an equation:
X + (X - 10) = 180
Combine like terms:
2X - 10 = 180
Add 10 to both sides:
2X = 190
Divide both sides by 2:
X = 95
So, angle a is 95 degrees and angle b is (95 - 10) = 85 degrees.
The angles are:
x = 95 and x = 85
Work/explanation:
The sum of two supplementary angles is 180°.
The angles are given as x and x - 10, so we form an equation with the given information.
\(\sf{x+x-10=180}\)
\(\sf{2x-10=180}\)
Simplify each side
\(\sf{2x=180+10}\)
\(\sf{2x=190}\)
\(\sf{x=95}\)
The other angle is x - 10 thus : 95 - 10 = 85.
Hence, the angles are 85 and 95°.Find the rectangular coordinates of the point whose spherical coordinates are given. (a) (3, 0, 0) (x, y, z) (b) (10, pi/3, pi/4)
Answers
the rectangular coordinates of the point whose spherical coordinates are given. (3, 0, 0) are (0.0.3)
What is spherical coordinates?
The coordinate system that is most frequently employed in three-dimensional systems is called spherical coordinates of the system, represented as (r,Ф,∅ ). The surface area in three dimensions is calculated using the spherical coordinate system. Radial distance, polar angles, and azimuthal angle are the three numbers that these coordinates indicate. Additionally known as spherical polar coordinates.
Given (r,Ф,∅ ) = (3,0,0)
x = rsin∅ cosФ = 3 * sin0 *cos0 = 0
y = rsin∅ sinФ = 3*0*0 = 0
z = rcos∅ = 3*1 = 3'
SO (x,y,y) = (0,0,3)
Hence the rectangular coordinates of the point whose spherical coordinates are given. (3, 0, 0) are (0.0.3)
Learn more about spherical coordinates, by the following link
https://brainly.com/question/4465072
#SPJ4
Will mark brainliest, rate and thank pls answer. I don't need an explanation just an answer 3t+8(2t-6)=12+14t 2v+18=16-4(v+7) 4x-(9-3x)=8x-1 12(3+y)=5(2y+8)
Answers
Answer:
see below
Step-by-step explanation:
3t+8(2t-6)=12+14t
Distribute
3t +16t-48 = 12+14t
Combine like terms
19t -48 = 12+14t
Subtract 14t from each side
5t -48 = 12
Add 48 to each side
5t = 60
Divide by 5
t =12
2v+18=16-4(v+7)
Distribute
2v+18 = 16 -4v -28
Combine like terms
2v +18 = -4v -12
Add 4v to each side
6v+18 = -12
Subtract 18 from each side
6v = -30
Divide by 6
v = -5
4x-(9-3x)=8x-1
distribute
4x -9+3x = 8x -1
Combine like terms
7x -9 = 8x -1
Subtract 7x from each side
-9 = x-1
Add 1 to each side
-8 =x
12(3+y)=5(2y+8)
Distribute
36 +12y = 10y +40
Subtract 10y from each side
36+2y = 40
Subtract 36 from each side
2y =4
Divide by 2
2y/2 = 4/2
y =2
If there are 13400 students at Rocky Valley College and 1/4
take speech, how many students take a speech at rocky valley college
Answers
Answer:
three thousand three hundred and fifty.3,350
Step-by-step explanation:
the question given was:1/4 take a speech, so how many?: one fourth, if you divide 13,400 by 4 its 3,350. that is one fourth of 13,400. So, if you add 3,350 four times, it would be 13,400.
Hope this helped!<3
The spinner below is spun 1 time and the number cubes is rolled 1 time. What is the probability of the spinner landing in a green and rolling a number less than 3?
Answers
Answer:
unlikely
Step-by-step explanation:
because the sooner is only spun once while the cube is only roles once as well.
Which value of x makes the following equation true?
3(x-3) = -2x + 31
Answers
Answer:
x=8
Step-by-step explanation:
1. Distribute the 3 into the (x-3) to have 3x-9 = -2x+31
2. Add 9 to each side to get 3x = -2x+40
3. Add 2x to each side to get 5x = 40
4. Divide each side by 5 to get x=8
Solving for the value of x,
→ 3(x - 3) = -2x + 31
→ 3x - 9 = -2x + 31
→ 3x + 2x = 31 + 9
→ 5x = 40
→ x = 40/5
→ [ x = 8 ]
Thus, the value of x is 8.
Image transcription textSuppose the following two simple statements are true.
The scroll is open.
The writings are visible.
Determine which of the following compound statements would also be true. Select all that apply.
Answer
The scroll is not open or the writings are visible.
" The scroll is open or the writings are not visible.
The scroll is open or the writings are visible.
1 The scroll is not open or the writings are not visible.... Show more
Answers
Based on the given simple statements, "The scroll is open" and "The writings are visible," we can determine which compound statements would also be true.
The scroll is not open or the writings are visible.
This compound statement would be true. Since the first simple statement states that the scroll is open, the negation of this statement would be that the scroll is not open. The second simple statement states that the writings are visible, which aligns with this compound statement. Therefore, this compound statement is true.
The scroll is open or the writings are not visible.
This compound statement would not be true. Both simple statements state that the scroll is open and the writings are visible. So, the second part of this compound statement contradicts the given information.
The scroll is open or the writings are visible.
This compound statement would be true. It directly matches the given simple statements, where both the scroll being open and the writings being visible are mentioned. Therefore, this compound statement is true.
The scroll is not open or the writings are not visible.
This compound statement would not be true. Both simple statements state that the scroll is open and the writings are visible. So, neither part of this compound statement aligns with the given information.
The compound statements that would be true are:
The scroll is not open or the writings are visible.
The scroll is open or the writings are visible.
To know more about compound statements , visit;
https://brainly.com/question/29098482?referrer=searchResult
#SPJ11
Please help me with this.
Consider the function f(x)= -3x^3-4x^2+x+2
A partial graph is shown below, find all the zeros of the function using division and factoring. Please show all work.
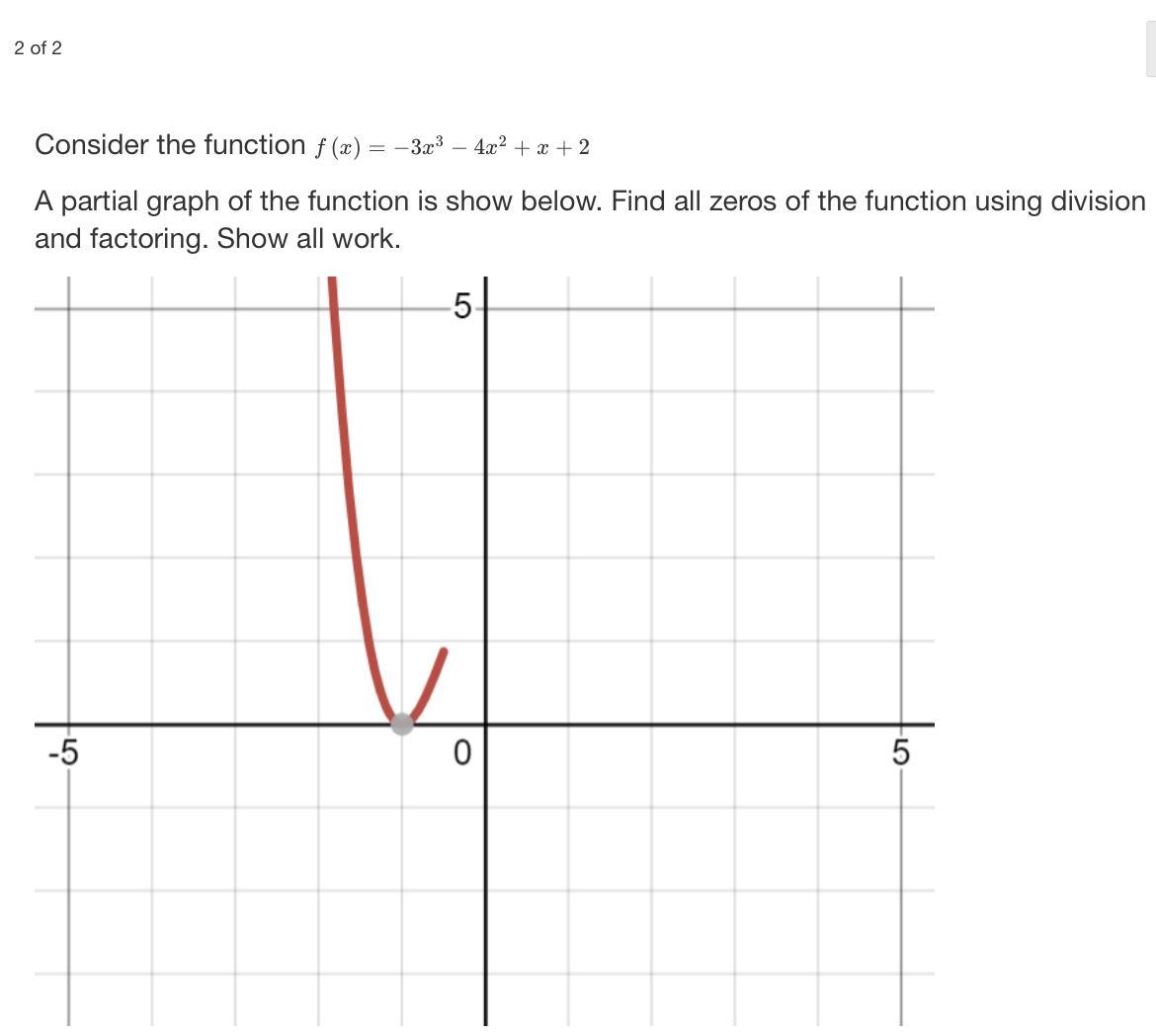
Answers
Using division and the graph, the zeroes of the function are given as follows:
x = -1 with multiplicity 2.x = 2/3 with multiplicity 1.How do we find all the zeros of the function?The function in this problem is defined as follows:
f(x) = -3x³ -4x² + x + 2.
From the graph, we have that x = -1 is a zero of the function, meaning that it can be written as follows:
-3x³ -4x² + x + 2 = (x + 1)(ax² + bx + c).
The other zeros will be the zeros of ax² + bx + c. To find the coefficients, we use a system of equations, hence:
(x + 1)(ax² + bx + c) = -3x³ -4x² + x + 2
ax³ + (a + b)x² + (c + b)x + c = 2.
Hence the coefficients are given by:
a = -3.c = 2.a + b = -4 -> b = -1.Thus the quadratic equation that we have to solve is:
-3x² - x + 2 = 0
3x² + x - 2 = 0.
Hence:
\(\Delta = 1^2-4(3)(-2) = 25\)\(x_1 = \frac{-1 + \sqrt{25}}{6} = \frac{2}{3}\)\(x_2 = \frac{-1 - \sqrt{25}}{6} = -1\)The zeroes of the function are given as follows:
x = -1 with multiplicity 2.x = 2/3 with multiplicity 1.More can be learned about the zeroes of a function at https://brainly.com/question/65114
#SPJ1
For what amount of exit proceeds would these two structures yield the same amount of carried interest?
.20 (Z-250) = .30 (Z-200)
Solve for Z.
Answers
Answer:
Step-by-step explanation:"To solve this equation, you can start by distributing the 0.20 and 0.30 terms. Then, you can simplify the equation by combining like terms. After that, you can isolate the variable Z on one side of the equation by adding or subtracting terms from both sides. Finally, you can solve for Z. The solution is Z = 1000. Does that help?"
Indicate if the following would result in a random sample or a biased sample
Use a pattern, such as selecting every fourth person who enters the cafeteria
A. biased
B. random
Answers
Answer:
biased
Step-by-step explanation:
i took the test and I got it right
f(x) = 14 - 0.5x f (30)
Answers
Answer:
- 1
Step-by-step explanation:
\(f(x) = 14 - 0.5x \\ f(30) = 14 - 0.5 \times 30 \\ f(30) = 14 - 15 \\ f(30) = - 1 \\ \)
example 2 major premise: no dogmatists are scholars who encourage free thinking. minor premise: some theologians are scholars who encourage free thinking. conclusion: some theologians are not dogmatists. the major premise in example 2 is an proposition. the minor premise in example 2 is an proposition. the conclusion in example 2 is an proposition. therefore, the mood of the categorical syllogism in example 2 is .
Answers
The mood of the categorical syllogism in example 2 is AIO.
In your example, we have the following premises and conclusion:
1. Major Premise: No dogmatists are scholars who encourage free thinking.
2. Minor Premise: Some theologians are scholars who encourage free thinking.
3. Conclusion: Some theologians are not dogmatists.
The major premise in example 2 is an A proposition (All S are not P). The minor premise in example 2 is an I proposition (Some S are P). The conclusion in example 2 is an O proposition (Some S are not P).
To learn more about premises, refer here:
https://brainly.com/question/29699382#
#SPJ11
what are the possible numbers of minutes he has used his phone in a month? use for the number of minutes, and solve your inequality for .
Answers
Inequality is a statement of an order relationship between two figures or algebraic expressions. Ryan used at least 1189 minutes.
In mathematics, an inequality is a relation which makes a non-equal comparison between two figures or other fine expressions. It's used most frequently to compare two figures on the number line by their size.
Given
Let m be the number of minutes used.
Yearly cost = fixed cost variable cost
fixed cost = 13
Variable cost = 0.05 × m
Yearly cost = 130.05 m
It says in the problem that the least he has been charged in a month is$72.45.
This means that the yearly cost is at least72.45.
In other words, the yearly cost is72.45 or bigger.
This can be expressed as 130.05 m ≥72.45
130.05 m ≥72.45
13- 130.05 m ≥72.45- 13
00.05 m ≥72.45- 13
m ≥59.45
Divide both sides by0.05
m/0.05 ≥59.45/0.05
m ≥ 1189
thus, Ryan used at least 1189 minutes
Question
For his phone service, Ryan pays a yearly figure of$13.00, and he pays an fresh$0.05 per nanosecond of use. The least he has been charged in a month is$72.45. What are the possible figures of twinkles he has used his phone in a month?
Use m for the number of twinkles, and break your inequality form.
To know more about Inequality,
brainly.com/question/30238989
# SPJ4
find the length of the curve. r(t) = cos(6t) i + sin(6t) j + 6 ln(cos(t)) k, 0 ≤ t ≤ π/4
Answers
The length of the curve is given by the integral of the square root of the sum of the squares of the derivatives of each component of r(t), integrated over the given interval, length is 6 units.
In this case, we have
r(t) = cos(6t) i + sin(6t) j + 6 ln(cos(t)) k, and we need to find the length of the curve from t = 0 to t = π/4.
Using the arc length formula, we have the integrand as the square root of (-6sin(6t))^2 + (6cos(6t))^2 + (-6sin(t) / cos(t))^2.
Simplifying the integrand, we get √(36sin²(6t) + 36cos²(6t) + 36sin²(t) / cos²(t)).
Further simplifying, we have √(36 + 36sin²(t) / cos²(t)).
By applying trigonometric identities, we can rewrite the integrand as √(36cos²(t) + 36sin²(t) / cos²(t)).
Simplifying further, we obtain √(36 + 36tan²(t)).
Now,
∫√(36 + 36u²) du / (1 + u²).
Now, we can simplify the integrand:
√(36 + 36u²) / (1 + u²).
Next, we can factor out 36 from the square root:
√36(1 + u²) / (1 + u²).
Simplifying further, we get:
√36 = 6, so the integral becomes:
6∫(1 + u²) / (1 + u²) du.
Notice that the expression (1 + u²) / (1 + u²) simplifies to 1, so the integral reduces to:
6∫du.
Integrating du gives us u + C, where C is the constant of integration.
Therefore, the indefinite integral of √(36 + 36tan²(t)) dt is 6(tan(t)) + C.
To evaluate the definite integral over the interval from 0 to π/4, we substitute the upper and lower limits:
[6(tan(π/4)) - 6(tan(0))] = [6(1) - 6(0)] = 6.
Hence, the length of the curve defined by the given vector function over the interval from 0 to π/4 is 6.
To learn more about arc length formula click here: brainly.com/question/30760398
#SPJ11
4. Show that the matrix [XX-X'Z(ZZ)-¹Z'X). where both the x & matrix X and the x matrix Z. have full column rank and m2, is positive definite. Discuss the implications of this result in econometrics.
Answers
To show that the matrix A = [XX - X'Z(ZZ)^(-1)Z'X] is positive definite, we need to demonstrate two properties: (1) A is symmetric, and (2) all eigenvalues of A are positive.
Symmetry: To show that A is symmetric, we need to prove that A' = A, where A' represents the transpose of A. Taking the transpose of A: A' = [XX - X'Z(ZZ)^(-1)Z'X]'. Using the properties of matrix transpose, we have:
A' = (XX)' - [X'Z(ZZ)^(-1)Z'X]'. The transpose of a sum of matrices is equal to the sum of their transposes, and the transpose of a product of matrices is equal to the product of their transposes in reverse order. Applying these properties, we get: A' = X'X - (X'Z(ZZ)^(-1)Z'X)'. The transpose of a transpose is equal to the original matrix, so: A' = X'X - X'Z(ZZ)^(-1)Z'X. Comparing this with the original matrix A, we can see that A' = A, which confirms that A is symmetric. Positive eigenvalues: To show that all eigenvalues of A are positive, we need to demonstrate that for any non-zero vector v, v'Av > 0, where v' represents the transpose of v. Considering the expression v'Av: v'Av = v'[XX - X'Z(ZZ)^(-1)Z'X]v
Expanding the expression using matrix multiplication : v'Av = v'X'Xv - v'X'Z(ZZ)^(-1)Z'Xv. Since X and Z have full column rank, X'X and ZZ' are positive definite matrices. Additionally, (ZZ)^(-1) is also positive definite. Thus, we can conclude that the second term in the expression, v'X'Z(ZZ)^(-1)Z'Xv, is positive definite.Therefore, v'Av = v'X'Xv - v'X'Z(ZZ)^(-1)Z'Xv > 0 for any non-zero vector v. Implications in econometrics: In econometrics, positive definiteness of a matrix has important implications. In particular, the positive definiteness of the matrix [XX - X'Z(ZZ)^(-1)Z'X] guarantees that it is invertible and plays a crucial role in statistical inference.
When conducting econometric analysis, this positive definiteness implies that the estimator associated with X and Z is consistent, efficient, and unbiased. It ensures that the estimated coefficients and their standard errors are well-defined and meaningful in econometric models. Furthermore, positive definiteness of the matrix helps in verifying the assumptions of econometric models, such as the assumption of non-multicollinearity among the regressors. It also ensures that the estimators are stable and robust to perturbations in the data. Overall, the positive definiteness of the matrix [XX - X'Z(ZZ)^(-1)Z'X] provides theoretical and practical foundations for reliable and valid statistical inference in econometrics.
To learn more about eigenvalues click here: brainly.com/question/29861415
#SPJ11
A random survey asked two samples of 100 high school students how much time they spend on homework each night. A 4-column table with 2 rows.
Answers
The time categories are divided into "<1 hour," "1-2 hours," "2-3 hours," and ">3 hours."
What does the frequency distribution in the table reveal about the homework habits of the two samples of high school students?
The frequency distribution in the table provides insights into the distribution of homework habits among the two samples of high school students. By examining the frequency counts in each time category, we can determine the proportion of students spending different amounts of time on homework each night. This information helps identify patterns and differences in homework habits between the two samples, allowing for a comparison of their study behaviors.
Here is an example of a 4-column table with 2 rows representing the results of a random survey asking two samples of 100 high school students about the amount of time they spend on homework each night:
Sample 1:
Sample 1 Number of Students
Time Frequency
<1 hour 20
1-2 hours 40
2-3 hours 30
>3 hours 10
Sample 2:
Sample 2 Number of Students
Time Frequency
<1 hour 30
1-2 hours 35
2-3 hours 20
>3 hours 15
In this table, each sample represents a different group of 100 high school students, and the frequency of students spending a particular amount of time on homework each night is recorded. The time categories are divided into "<1 hour," "1-2 hours," "2-3 hours," and ">3 hours." The table provides an overview of the distribution of homework time among the two samples of high school students.
To learn more about the frequency distribution from the given link
brainly.com/question/27820465
#SPJ4
Ethan buys a video game on sale. if the video game usually costs $39.99, and it was on sale for 20% off, how much did ethan pay? round to the nearest cent.
Answers
Amount paid by Ethan to buy a video game on sale of 20% with usual cost of $39.99 is equal to $32 ( nearest cent ).
As given in the question,
Usual cost of Video game bought by Ethan = $39.99
Sale discount received by Ethan on video game = 20%
Let 'x' be the amount paid by Ethan for video game.
Discount amount = 20% of $39.99
= ( 20 / 100 ) × 39.99
= 799.8/100
= $ 7.998
= $7.99
Amount to be paid by Ethan 'x' = $39.99 - $7.99
= $32 ( nearest cent)
Therefore, the amount paid by Ethan to purchase a video game on sale discount of 20% is given by $32.
Learn more about sale here
brainly.com/question/29442509
#SPJ4
determine the angle of rotation at the point z0 = 2 i when w = z 2
Answers
The angle of rotation at the point \(\(z_0 = 2i + 1\)\) when \(\(w = z^2\)\) is \(\(2\arctan(2)\),\) which is approximately 1.107 radians or 63.43 degrees.
To determine the angle of rotation at the point \(\(z_0 = 2i + 1\)\) when \(\(w = z^2\),\) we can follow these steps:
1. Express \(\(z_0\)\) in polar form: To find the polar form of \(\(z_0\)\), we need to calculate its magnitude \((\(r_0\))\) and argument \((\(\theta_0\))\). The magnitude can be obtained using the formula \(\(r_0 = |z_0| = \sqrt{\text{Re}(z_0)^2 + \text{Im}(z_0)^2}\)\):
\(\[r_0 = |2i + 1| = \sqrt{0^2 + 2^2 + 1^2} = \sqrt{5}\]\)
The argument \(\(\theta_0\)\) can be found using the formula \(\(\theta_0 = \text{arg}(z_0) = \arctan\left(\frac{\text{Im}(z_0)}{\text{Re}(z_0)}\right)\)\):
\(\[\theta_0 = \text{arg}(2i + 1) = \arctan\left(\frac{2}{1}\right) = \arctan(2)\]\)
2. Find the polar form of \(\(w\)\): The polar form of \(w\) can be expressed as \(\(w = |w|e^{i\theta}\)\), where \(\(|w|\)\) is the magnitude of \(\(|w|\)\) and \(\(\theta\)\) is its argument. Since \((w = z^2\)\), we can substitute z with \(\(z_0\)\) and calculate the polar form of \(\(w_0\)\)using the values we obtained earlier for \(\(z_0\)\):
\(\[w_0 = |z_0|^2e^{2i\theta_0} = \sqrt{5}^2e^{2i\arctan(2)} = 5e^{2i\arctan(2)}\]\)
3. Determine the argument of \(\(w_0\):\) To find the argument \(\(\theta_w\)\) of \(\(w_0\)\), we can simply multiply the exponent of \(e\) by 2:
\(\[\theta_w = 2\theta_0 = 2\arctan(2)\]\)= 1.107 radians
Therefore, the angle of rotation at the point \(\(z_0 = 2i + 1\)\) when \(\(w = z^2\)\) is \(\(2\arctan(2)\).\)
Learn more about exponent here: https://brainly.com/question/29277932
#SPJ11
The complete question is:
"Determine the angle of rotation, in radians and degrees, at the point z0 = 2i + 1 when w = z^2."