is 3.66227766017 rational or irrational?
Answers
Answer:
I think it's irrational (viewpoint)
Related Questions
Part II. Jacob tells you that there is a 40% probability that at least two people in each classroom of 25 students share a birthday (ignore leap years). You don’t believe Jacob and decide to conduct a simulation to see if you get enough evidence to reject his claim.
• State the null hypothesis and the alternative hypothesis.
Use the random number generator to do a simulation and do this simulation 16 times. Record your results in the table below. In each simulation you will be checking how many couple of students share a birthday.
Find the proportion of “classrooms” with at least a couple of students sharing a birthday.
• Find the t-statistic:
Compare P-value (probability of getting a value at least as extreme as your t-statistic under the null hypothesis) with the a level:
• State your conclusion:

Answers
Null hypothesis: The probability of at least two people in each classroom of 25 students sharing a birthday is less than or equal to 40%.
Alternative hypothesis: The probability of at least two people in each classroom of 25 students sharing a birthday is greater than 40%.
What are the results from the simulations?Simulation Results:
Simulation 1: 8 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 2: 9 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 3: 7 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 4: 11 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 5: 7 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 6: 6 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 7: 8 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 8: 6 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 9: 10 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 10: 8 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 11: 7 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 12: 11 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 13: 8 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 14: 7 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 15: 10 out of 16 classrooms had at least 2 students sharing a birthday.
Simulation 16: 10 out of 16 classrooms had at least 2 students sharing a birthday.
Proportion of classrooms with at least 2 students sharing a birthday = (8+9+7+11+7+6+8+6+10+8+7+11+8+7+10+10)/16 = 0.7125
The mean number of classrooms with at least 2 students sharing a birthday is 0.7125. We can use this value to calculate the t-statistic.
t-statistic = (0.7125 - 0.4) / (sqrt(0.4 * 0.6 / 16)) = 5.766
Using a one-tailed t-test with 15 degrees of freedom and an alpha level of 0.05, the critical t-value is 1.753. Since the calculated t-statistic is greater than the critical t-value, we can reject the null hypothesis.
The p-value is very small (less than 0.0001), indicating strong evidence against the null hypothesis.
Therefore, we can conclude that there is sufficient evidence to suggest that the probability of at least two people in each classroom of 25 students sharing a birthday is greater than 40%.
learn more about t-statistic: https://brainly.com/question/6589776
#SPJ1
find the area of the pentagon in the diagram below.
15 square inches
20 square inches
25 square inches
28 square inches

Answers
The area of the pentagon is approximately 15 square inches.
To find the area of the pentagon, we can use the formula for the area of a regular pentagon:
Area = (5/4) * (s²) * (1/tan(π/5)),
where "s" is the length of the side of the pentagon.
Given that the sides of the pentagon are as follows:
Two smallest sides = 2 inches,
Two largest equal sides = 4 inches,
One other equal side = 3 inches.
Since the pentagon is not a regular pentagon, we need to find the area by dividing it into different shapes and then calculating their individual areas.
The pentagon can be divided into three shapes: a rectangle and two triangles.
Rectangle:
The two smallest sides (2 inches) form the length and width of the rectangle.
Area of the rectangle = Length * Width = 2 inches * 2 inches = 4 square inches.
Triangle 1:
The two largest equal sides (4 inches) and one of the 3-inch sides form a triangle.
To calculate the height (h) of the triangle, we can use the Pythagorean theorem, since it is a right triangle.
h² = (4 inches)² - (1.5 inches)², [1.5 inches is half of the 3-inch side]
h² = 16 inches² - 2.25 inches²,
h² = 13.75 inches²,
h ≈ 3.7 inches.
Area of Triangle 1 = (1/2) * Base * Height = (1/2) * 3 inches * 3.7 inches ≈ 5.55 square inches.
Triangle 2:
The two largest equal sides (4 inches) and the other 3-inch side form another triangle.
Using the same height (3.7 inches) from Triangle 1:
Area of Triangle 2 = (1/2) * Base * Height = (1/2) * 3 inches * 3.7 inches ≈ 5.55 square inches.
Now, to find the area of the pentagon, we add the areas of the rectangle and the two triangles:
Total Area = Area of Rectangle + Area of Triangle 1 + Area of Triangle 2
Total Area = 4 square inches + 5.55 square inches + 5.55 square inches
Total Area ≈ 15.1 square inches.
Therefore, the area of the pentagon is approximately 15.1 square inches.
To know more about area of the pentagon click here :
https://brainly.com/question/29683405
#SPJ2
True or False? The blue radius is perpendicular to the green cord.

Answers
Answer:
true
Step-by-step explanation:
Answer:
False. if it was perpendicular than the segments would be equal
Step-by-step explanation:
A group of friends were working on a student film that had a budget of $800. They spent all their budget on props and equipment. They used 83% of their budget on equipment. How much money did they spend on props?
Answers
Answer:
$136
Step-by-step explanation:
100% - 83% = 17%
the 17% is on props.
so, take 17/100 and multiply with $800, which you will get 136.
so the amount of money spent on props is $136
The population of Brazil is about 2 x 108. The population of Argentina is about 4 × 107.
How many times larger is the population of Brazil than the population of Argentina?
O 10
02
05
07
Answers
The population of brazil is 5 times more than the population of Argentina
What is population?
The term "population" usually refers to the total number of people living in a particular area, such as a city or town, region, nation, continent, or the entire world. Governments frequently use censuses, a procedure for gathering, analysing, compiling, as well as publishing data regarding a population, to determine the size of a resident population inside their jurisdiction.
We are given that the population of argentine is \(4\)×\(10^7\)
And the population of brazil is \(2\)×\(10^8\)
Now we are asked to find How many times larger is the population of Brazil than the population of Argentina
Now Population of brazil can also be written as \(20\)×\(10^7\)
Now we take the ratio of population of brazil and population of argentine
We get,
\(\frac{20}{4}\)×\(\frac{10^7}{10^7}\)
=5
Hence, population of Brazil is 5 times larger than the population of Argentina
Hence the correct option is option c) 5
To learn more about population please refer
https://brainly.com/question/25896797
#SPJ13
Let's assume the average speed of a serve in women's tennis is around 118 mph, with a standard deviation of 12 mph. We recruit 100 amateur tennis players to use our method this time, and after 6 months we calculate a group mean of 123 mph.
Reference: 8.54 More about confidence intervals, effect sizes, and tennis serves
a. Based on the 95% confidence interval computed in #5, which statement best reflects the findings. (Read each option carefully)
A. Because the population mean of 118 mph falls within the confidence interval around the new mean, we can not conclude that the program had an impact. We do not have evidence to support that it changed the speed of a tennis serve.
B. Because the population mean of 118 mph does not fall within the confidence interval around the new mean, we can not conclude that the program had an impact. We do not have evidence to support that it changed the speed of a tennis serve.
C. Because the population mean of 118 mph falls within the confidence interval around the new mean, we can conclude that the program had an impact. In fact, we can conclude that the program seemed to increase the average speed of women’s serves.
D. Because the population mean of 118 mph does not fall within the confidence interval around the new mean, we can conclude that the program had an impact. In fact, we can conclude that the program seemed to increase the average speed of women’s serves.
Answers
The correct answer is (D) Because the population mean of 118 mph does not fall within the confidence interval around the new mean, we can conclude that the program had an impact. In fact, we can conclude that the program seemed to increase the average speed of women’s serves.
Because the population mean of 118 mph does not fall within the confidence interval around the new mean, we can conclude that the program had an impact. In fact, we can conclude that the program seemed to increase the average speed of women’s serves.
The confidence interval around the group mean of 123 mph suggests that the true population mean lies somewhere within a certain range. Since the lower limit of this range is above the population mean of 118 mph, we can infer that the program had a positive impact on the participants' average serve speed.
This suggests that the program was successful in improving the participants' skills and abilities in tennis, resulting in faster serves.
To know more about confidence interval, refer the link:
https://brainly.com/question/24131141#
#SPJ11
Hey! Been stuck on this problem, if anyone could helpThe officers of a high school senior class are planning to rent buses and vans for a class trip. Each bus can transport 70 students, requires 6 chaperones, and costs $1300 to rent. Each van can transport 10 students, requires 1 chaperone, and costs $80 to rent. Since there are 630 students in the senior class that may be eligible to go on the trip, the officers must plan to accommodate at least 630 students. Since only 60 parents have volunteered to serve as chaperones, the officers must plan to use at most 60 chaperones. How many vehicles of each type should the officers rent in order to minimize the transportation costs? What are the minimal transportation costs?The officers should rent how many buses and how many vans to minimize the transportation costs
Answers
hello
to solve this question, we need to write down details we have first in order to take some key facts into consideration.
1 bus (70 students + 6 chaperones) = $1300
1 van (10 students +1 chaperone) = $80
we have to take into consideration that the trip can only accomodate only 60 chaperone and also find the least expensive options to take.
the total number of students in senior class = 630 students
the best option would be to pick 7 buses and 15 vans
7 buses would be
\(\begin{gathered} 7\text{ buses} \\ 70\times7=490\text{ students} \end{gathered}\)7 buses would accomodate 490 students and will require
\(7(\text{buses)}\times6\text{ chaperones }=42\)7 buses will accomodate 490 students and would require 42 chaperones.
now we would need at least 14 vans to accomodate the remaining students.
\(\begin{gathered} 14\text{ buses} \\ 10(\text{students)}\times14=140\text{ students} \end{gathered}\)14 vans would require a total of 14 chaperones
\(\begin{gathered} 7\text{ buses}=490\text{ students and 42 chaperones} \\ 14\text{ vans}=140\text{ students and 14 chaperones} \\ \text{total number of students = 630 students} \\ \text{total number of chaperones required = 42 + 14 =56} \end{gathered}\)now we can calculate the cost of the journey
\(\begin{gathered} 1\text{ bus costs =\$1300} \\ 7\text{ buses = 7}\times\text{ \$1300}=\text{ \$9,100} \\ 1\text{ van costs =\$80} \\ 14\text{ vans will cost = 14}\times\text{ \$80}=\text{ \$1,120} \\ \text{total costs = \$9,100 + \$1,120}=\text{ \$10,220} \end{gathered}\)from the calculations above, the minimal cost of the journey is $10,220 and
Ajar contains 3 white marbles, 5 orange marbles, 4 yellow marbles, and 2 black marbles. If a marble is drawn at random, find the probability that the marble is not yellow. What is the probability that the marble is not yellow? (Simplify your answer. Type an integer or a fraction.)
Answers
Answer:
10/14
Step-by-step explanation:
See 3 +5+4+2= 14 , if the question would be what's the probability of getting yellow the answer would be 4/14 but it's not, so 14 - 4 which will be 10 so 10 / 14 .
The other way is get the sum of all the marbles except the yellow one, then that no. will be upon the total.
Answer: \(\frac{2}{7}\)or 0.2857142857
Step-by-step explanation:
P(not yellow)=\(\frac{4}{14}\)
P(not yellow)=\(\frac{2}{7}\) or 0.2857142857
A student tells you that the sets of numbers below are listed in the following order: n; l; ml ; ms
Which one of these combinations is not a valid proposed set of quantum numbers for an electron?
Group of answer choices
a. 3; 2; 1; -1/2
b. 4; 3; 3; 1/2
c. 1; 0; 0; -1/2
d. 2; 0; 0; 1/2
e. 2; 0; 1; 1/2
Answers
The combination that is not a valid proposed set of quantum numbers is b.
The valid range of values for the quantum numbers are:
- n can be any positive integer (1, 2, 3, ... )
- l can be any integer from 0 to n-1
- ml can be any integer from -l to +l
- ms can be either +1/2 or -1/2
The valid ranges for each quantum number are as follows:
n (principal quantum number): Any positive integer
l (azimuthal quantum number): 0 to (n - 1)
ml (magnetic quantum number): -l to l
ms (spin quantum number): -1/2 or 1/2
Let's check each proposed set of quantum numbers:
a. 3; 2; 1; -1/2 - This set is valid. The values for n, l, ml, and ms are within the valid ranges.
b. 4; 3; 3; 1/2 - This set is not valid. The value of l (azimuthal quantum number) cannot be greater than n - 1. In this case, l is 3, which is greater than n - 1 (4 - 1 = 3). Therefore, this set is not valid.
c. 1; 0; 0; -1/2 - This set is valid. The values for n, l, ml, and ms are within the valid ranges.
d. 2; 0; 0; 1/2 - This set is valid. The values for n, l, ml, and ms are within the valid ranges.
e. 2; 0; 1; 1/2 - This set is valid. The values for n, l, ml, and ms are within the valid ranges.
To know more about integer, visit:
https://brainly.com/question/490943
#SPJ11
This is my homework and i need help asap

Answers
Using the segment addition postulate, it is found that:
1. Point B is between the other two.
2. The measures are: RS = 5, RT = 10, PR = 10, PQ = 6.
3. The value of x is of x = 9.5.
4. The value of y is of y = ± 5.
What is the segment addition postulate?The segment addition postulate is a geometry axiom that states that a line segment, divided into a number of smaller segments, has the length given by the sum of the lengths of the segments.
In item 1, we have that the largest segment is of AC, hence it represents the line, while point B splits the segment into two parts, that is, point B is between the other two.
In item 2, we have that:
S is the midpoint of RT, hence RS = ST = 5.For the same reason above, RT = RS + ST = 10.PR is congruent to RT, hence PR = 10.PR = PQ + QR -> PQ = PR - QR = 10 - 4 = 6.For item 3, applying the Postulate, we have that:
AB + BC + CD = AD
4 + 4 + 2x - 6 = 21
2x = 19
x = 9.5.
For item 4, due to the midpoint, we have that:
LM = MN
Hence:
y² + 4 = 29
y² = 25
y = ± sqrt(25)
y = ± 5.
More can be learned about the segment addition postulate at https://brainly.com/question/2134445
#SPJ1
in a survey of 2480 golfers, 15% said they were left-handed. the survey's margin of error was 3%. construct a confidence interval for the proportion of left-handed golfers.
Answers
The confidence interval for the proportion of left-handed golfers is of:
(0.12, 0.18).
How to obtain a confidence interval?A confidence interval is calculated as the sample mean plus/minus the margin of error, hence the bounds of the confidence interval are given as follows:
Lower bound: sample mean - margin of error.Upper bound: sample mean + margin of error.In the context of this problem, these parameters are given as follows:
Sample mean: 15% as a percentage, 0.15 as a proportion.Margin of error: 3% as a percentage, 0.03 as a proportion.Hence the lower bound of the confidence interval for the proportion of left-handed golfers is:
0.15 - 0.03 = 0.12.
The upper bound of the confidence interval for the proportion of left-handed golfers is:
0.15 + 0.03 = 0.18.
Then the interval is:
(0.12, 0.18).
More can be learned about confidence intervals at https://brainly.com/question/25890103
#SPJ1
Which transformation can be used to prove that this parallelogram is symmetrical?
Answers
Izzy has 354 grapes and 600 red grapes. The man in the store is selling apples. How many grapes are there in all?
Answers
:)))
SHEEEEEEEESH
Which situation can be represented by this equation?
250 + 65x = 575
F Jeremy Is traveling to a location that is 575 miles away. He has already traveled
250 miles. What is x, the number of hours that Jeremy will need to travel at a speed of
65 miles per hour to reach the location?
G Jeremy is traveling to a location that is 575 miles away. He has already traveled
250 mlles. What is x, the number of additional miles that Jeremy will need to travel to
reach the location?
H Jeremy is reading a book with 575 pages. He has already read 65 pages and will read
250 pages per day. What is x, the number of days that Jeremy will need to read to finish
the book?
) Jeremy is reading a book with 575 pages. He has already read 315 pages. What is x, the
number of pages Jeremy has left to read to finish the book?
Answers
The problem statement 1 → Jeremy Is traveling to a location that is 575 miles away. He has already traveled 250 miles. What is x, the number of hours that Jeremy will need to travel at a speed of 65 miles/hr to reach the location is the correct answer.
What is the general equation of straight line?The general equation of a straight line is -
y = mx + c
where -
m is the slope of line.
c is the y - intercept.
Given is a equation of a straight line → 250 + 65x = 575
Given equation is -
250 + 65x = 575
Rearranging the equation, we get -
575 = 65x + 250
Comparing it with the general equation of a straight line, we get -
y = 575
m = 65
c = 250
Now, if we look at the Problem 1 which states - Jeremy Is traveling to a location that is 575 miles away. He has already traveled 250 miles. What is x, the number of hours that Jeremy will need to travel at a speed of 65 miles/hr to reach the location.
250 miles → y - intercept
575 miles → y
65 miles/hr → m [representing rate]
Number of hours → x
Therefore, the problem statement 1 → Jeremy Is traveling to a location that is 575 miles away. He has already traveled 250 miles. What is x, the number of hours that Jeremy will need to travel at a speed of 65 miles/hr to reach the location is the correct answer.
To solve more questions on Equation modelling, visit the link below-
https://brainly.com/question/20534946
#SPJ2
What is the maximum area of a rectangle with a perimeter of 320 feet?
Answers
Answer:
For a rectangle of given perimeter, here 320 feet, the rectangle with the greatest are is the square. This square shall be 80 x 80. Maximum at (80, 6400)
Step-by-step explanation:
What conditions should you check to make sure that your linear model is reasonable? Select all that apply. A. Quantitative Variables Condition B. Straight Enough Condition C. Does the Plot Thicken? Condition ID. D. Outlier Condition
Answers
The conditions that should be checked to make sure that your linear model is reasonable are: Quantitative Variables Condition, Straight Enough Condition, Outlier Condition.
A. Quantitative Variables Condition: This condition requires that both the explanatory and response variables be quantitative, so that the relationship between them can be modeled with a straight line.
B. Straight Enough Condition: This condition requires that the relationship between the two variables be approximately linear, so that the linear model is a good fit for the data.
D. Outlier Condition: This condition requires that there are no outliers in the data that can significantly affect the linear model.
The "Does the Plot Thicken?" condition is not a valid condition for checking the reasonableness of a linear model.https://brainly.com/question/29665935
Learn more about regression analysis here:
#SPJ11
What’s the distance between (-2,3) and (2,1) ;; using distance formula
Answers
Answer:4.472136
Step-by-step explanation:

The formula in finding the distance between two points is given below:
\( \boxed{\bold{\:\:d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \:\:}}\)Now, you know the distance formula. So, let us try solving the given problem using the distance formula.
Problem: What is the distance between (-2, 3) and (2, 1), using the distance formula?
From inspection on the given problem:
\(\sf (x_1, y_1) = (-2, 3)\)\(\sf (x_2, y_2) = (2, 1)\)Substitute the given values into the distance formula and solve for d:
\(\sf d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\)\(\sf d = \sqrt{[2 - (-2)]^2 + (1 - 3)^2}\)\(\sf d = \sqrt{(4)^2 + (-2)^2}\)\(\sf d = \sqrt{16 + 4}\)\(\bold{d = \sqrt{20} \approx 4.47 \: units}\)Therefore, the distance between two points is 4.47 units.
\(\\\)
Now, wasn't that easy? Try this sample problem:
Find the distance between P(1, 3) and Q(7, 11).From the sample problem above, you may solve it on your own to enhance your skill on calculating the distance.
For more information about the Distance Formula, just visit this link: https://brainly.com/question/18156437
Help me plz plz plz

Answers
Answer:
C/5=5.2 and for the total is 26
Step-by-step explanation:
Because C is the total cost and is divided by 5 people so the answer C/5=5.2
Natalie is paid for writing numbers on pages of a book. She is paid for writing each digit of the number. If she wrote 702 digits, how many pages is the book?
Answers
Answer:
I think 1,000??
Find The slope
PLEASE HELP ME

Answers
Answer:
The slope is \(\frac{5}{2}\) (5/2)
Step-by-step explanation:
Key skills needed: Subtraction, Division, Slope Formula
1) So to find the slope here, we use the slope formula.
Given 2 points \((x_1, y_1)\) and \((x_2, y_2)\)
To find the slope you do: \(\frac{y_2-y_1}{x_2-x_1}\)
2) So in this case, the 2 points are (-1,-2) and (1,3)
3) We can use the slope formula to find the slope
-1 is \(x_1\)-2 is \(y_1\)1 is \(x_2\)3 is \(y_2\)Now we do \(\frac{y_2-y_1}{x_2-x_1}\)
This would be: \(\frac{3-(-2)}{1-(-1)}\)
If you are subtracting -2, that means you add 2. If you are subtracting -1, then that means you add 1.
This means ---> \(\frac{3+2}{1+1}\)
3+2 is 5, and 1+1 is 2 so your slope would be \(\frac{5}{2}\) (5/2)
Hope you understood and have a nice day!! :D
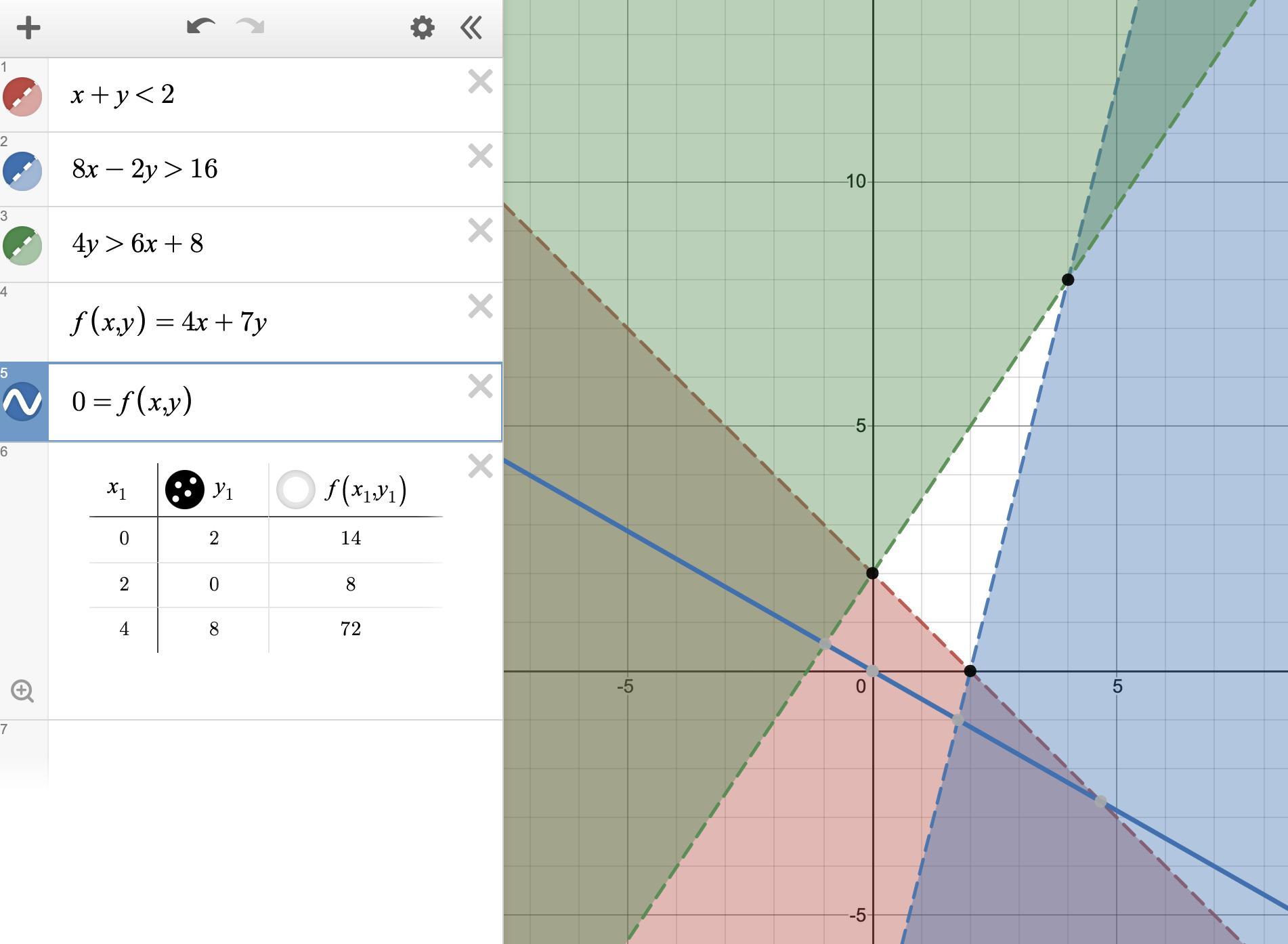
Find the maximum and minimum values of the function for the polygonal convex set determined by the given system of
inequalities.
x+y>2
8x-2y< 16
4y <6x+8
f (x, y) = 4x+7y

Answers
Answer:
max: 72 at (4, 8)
min: 8 at (2, 0)
Step-by-step explanation:
The attached graph shows the solution set as a white area. The shaded areas are excluded from the solution set. The dashed boundary lines indicate those lines are not excluded from the set. The vertices of the polygon are (0, 2), (2, 0) and (4, 8).
The line f(x,y) = 0 is shown for reference. The maximum value of f(x,y) will be found at the vertex of the solution set that is farthest from this line. The minimum will be found at the vertex of the solution set that is closest to this line.
The maximum value of f(x, y) is 72 at (x, y) = (4, 8).
The minimum value of f(x, y) is 8 at (x, y) = (2, 0).
What are the domain restrictions of q^2−7q−8 divided by q^2+3q−4 ?
o q≠1 and q≠−8
o q≠−1 and q≠8
o q≠−1 and q≠4
o q≠1 and q≠−4
Answers
The domain restrictions of the expression q²−7q−8/q²+3q−4 are q ≠ -4 and q ≠ 1. (option c)
The denominator of the expression is q²+3q−4. To determine the values that would make the denominator equal to zero, we can set it equal to zero and solve for q:
q² + 3q - 4 = 0
Now, we can factorize the quadratic equation:
(q + 4)(q - 1) = 0
To find the values of q, we set each factor equal to zero and solve for q:
q + 4 = 0 or q - 1 = 0
Solving these equations, we get:
q = -4 or q = 1
So, the values of q that would make the denominator equal to zero are q = -4 and q = 1. These are the values we need to exclude from the domain of the expression to avoid division by zero.
Therefore, the correct answer is option c) q ≠ 1 and q ≠ -4.
To know more about domain here
https://brainly.com/question/28599653
#SPJ4
Complete Question:
What are the domain restrictions of q²−7q−8/q²+3q−4?
a) q≠1 and q≠−8
b) q≠−1 and q≠4
c) q≠1 and q≠−4
d) q≠−1 and q≠8
Choose the slope and y-intercept that
correspond with the graph.

Answers
y-intercept: 4
find the future value of $750 deposited each month at 3.25% for 15 years
Answers
Answer:
P=1538.461
Step-by-step explanation:
do it by the formula of
I=PRT, I=750 R=3.25% T=15
Percents
Michael is leaving a 15% tip for his waitress. What percent of the
original price will he pay? Write your answer as a percent, decimal,
and fraction.
Answers
Answer:
115%, 1.15, 115/100
Step-by-step explanation:
Question is attached. Show workings

Answers
1/(1 - i) is equivalent to (1/2) - (1/2)i; (x, y) is equivalent to (-1, 3/2) and The value of (a + b) in a + ib = (2 - i)² is -1
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables. Types of equation are linear, quadratic, cubic and so on.
Complex numbers are in the form a + bi, where a is a real number and the real part of the complex number while b is a real number and the imaginary part of the complex number, i = √(-1)
Given:
1) z = 1/(1 - i)
multiplying by the conjugate of 1 - i which is (1 + i):
1/(1 - i) * (1 + i)/(1 + i)
= (1 + i)/(1 + 1)
= (1 + i)/2
= (1/2) - (1/2)i
1/(1 - i) is equivalent to (1/2) - (1/2)i
2) 2y + xi = 4 + x - i
Comparing the real and imaginary parts:
2y = 4 + x (1)
and:
x = -1
2y = 4 + x
2y = 4 + (-1)
2y = 3
y = 3/2
(x, y) is equivalent to (-1, 3/2)
3) a + ib = (2 - i)²
(2 - i)² = (2 - i)(2 - i) = 4 - 2i - 2i - 1
(2 - i)² = 3 - 4i
a + ib = (2 - i)² = 3 - 4i
a = 3, b = -4; a + b = 3 - 4 = -1
The value of (a + b) in a + ib = (2 - i)² is -1
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
Solve for brainlist ❤️❤️

Answers
Answer:
(68/4) multiply by 3601
Step-by-step explanation:
Menu
TRY IT
Review Mulitplying and Dividing with 4-Digit Numbers
Multiply.
3.748 x 4
Enter your answers in the boxes to complete the equation.
3,748 x 4 = ( + 700 + 40 + 8)x
E L. x 4 + 700 x 4 + 40 x +8x4
+ 2,800 + 160 + 32
Answers
The question is asking to multiply 3.748 by 4. To solve this, we can use the standard algorithm for multiplication. The final answer is 14,992.
Starting from the rightmost digit of 3.748, we multiply it by 4, which gives us 32. We write down the 2 in the ones place and carry-over the 3 to the next column. We then multiply the next digit (4) by 4 and add the carry-over from the previous calculation, which gives us 19. We write down the 9 in the tens place and carry-over the 1 to the next column. Continuing this process, we get 14 in the hundreds place and 2 in the thousands place. Therefore, 3.748 x 4 = 14,992.
To solve this problem, we can break down the multiplication into four separate calculations: 8 x 4, 4 x 4, 7 x 4, and 3 x 4. Starting from the rightmost digit of 3.748, we multiply 8 by 4, which gives us 32. We write down the 2 in the ones place and carry-over the 3 to the next column. Next, we multiply 4 by 4 and add the carry-over from the previous calculation, which gives us 19. We write down the 9 in the tens place and carry-over the 1 to the next column. Then, we multiply 7 by 4 and add the carry-over, which gives us 29. We write down the 9 in the hundreds place and carry-over the 2 to the next column. Finally, we multiply 3 by 4 and add the carry-over, which gives us 14. We write down the 4 in the thousands place and the final answer is 14,992.
To know more about standard algorithm visit :
https://brainly.com/question/11380908
#SPJ11
find the length of the missing triangle. round your answer to three decimal places
PLEASE HELP!

Answers
Answer:
There is just one simple rules for find other side
Step-by-step explanation:
Think about a triangle and this triangle has 3 side it must have 90° on one edge. We assume the longest side is hipotenus x²+y²=hipotenus² . Look at your question hipotenus is 15 lets try to find other side. X²+12²=15² x=9
You want to borrow three rock CDs from your friend. She loves math puzzles and she always makes you solve one before you can borrow her stuff. Here's the puzzle: Before you borrow three CDs, she will have 39 CDs. She will have half as many country CDs as rock CDs, and one-fourth as many soundtracks as country CDs. How many of each type of CD does she have after you borrow three rock CDs?
Answers
Answer:
Rock CD's=21
Country CD's=12
Soundtrack CD's=3
Step-by-step explanation:
let
r= rock CD's
c = country CD's
s = soundtrack CD's
Total CD's=r + c + s =39
2c=r
c/4=s
2c+c+c/4=39
8c+4c+c=156
13c=156
c=12
Substitute c=12 into 2c=r
2c=r
3(12)=r
24=r
r=24
Substitute c=12 into c/4=s
c/4=s
12/4=s
3=s
s=3
Therefore, she has
c=12
s=3
r=24
before she borrowed you 3 rock CD's
Sha has
r=21
s=3
c=12
after you borrowed 3 rock CD's