In which number is the value of the 5 ten time the value of the 5 in 10.059
Answers
Answer:
The 5 in the number is in the hundreths place
so if wou miltipy the value by 10, it will be in the tenths place
Step-by-step explanation:
pic has place value chart

Related Questions
The table summarizes results from 990 pedestrian deaths that were caused by automobile accidents.
Driver
Intoxicated? Pedestrian Intoxicated?
Yes No
Yes 43 73
No 282 592
If one of the pedestrian deaths is randomly selected, find the probability that the pedestrian was intoxicated or the driver was not intoxicated.
Report the answer as a percent rounded to one decimal place accuracy. You need not enter the "%" symbol.
prob =
%
Answers
The total number of pedestrian deaths where the pedestrian was intoxicated or the driver was not intoxicated is 73 + 116 = 189.
The probability that the pedestrian was intoxicated or the driver was not intoxicated is prob = 19.1%.
The probability that the pedestrian was intoxicated or the driver was not intoxicated need to add the probabilities of two mutually exclusive events:
The pedestrian was intoxicated and the driver was not intoxicated.
The pedestrian was intoxicated and the driver may or may not have been intoxicated (i.e., the driver was either intoxicated or not intoxicated).
The first event corresponds to the cell in the table where the pedestrian was intoxicated and the driver was not intoxicated has a frequency of 73.
The second event corresponds to the sum of the frequencies in the cells where the pedestrian was intoxicated regardless of the driver's state of intoxication.
This is the sum of the frequencies in the cells (43, 73) is 116.
The total number of pedestrian deaths in the table is 990.
So, the probability that the pedestrian was intoxicated or the driver was not intoxicated is:
prob = 189/990 × 100% = 19.1%
The probability is 19.1%.
prob = 19.1
For similar questions on intoxicated
https://brainly.com/question/13614186
#SPJ11
Helppppp BRAINLEST if right ASAP

Answers
Answer:
21.9
Step-by-step explanation:
Running at a constant rate, 6 machines can produce 100 boxes of chewing gums in 8 hours . How many more minutes is required to complete the same job with 5 such machines ?
Answers
Answer:
96 more minutes are required to complete the same job with 5 such machines
Step-by-step explanation:
Proportions
We know 6 machines produce 100 boxes of chewing gum in 8 hours. For convenience, we'll work in minutes instead of hours.
The time needed for the 6 machines to complete the job is 8*60=480 minutes.
Considering proportions, if 6 machines complete the job in 480 minutes, then ONE machine would need 6*480 = 2880 minutes.
Now consider 5 such machines working. The time needed would reduce by a factor of 5: 2880/5=576 minutes
Now we know 5 machines would take 576 minutes. That is a difference of 576 - 480 = 96 minutes. Thus,
96 more minutes are required to complete the same job with 5 such machines
I’m trying to do old homework for fun but now I’m stuck
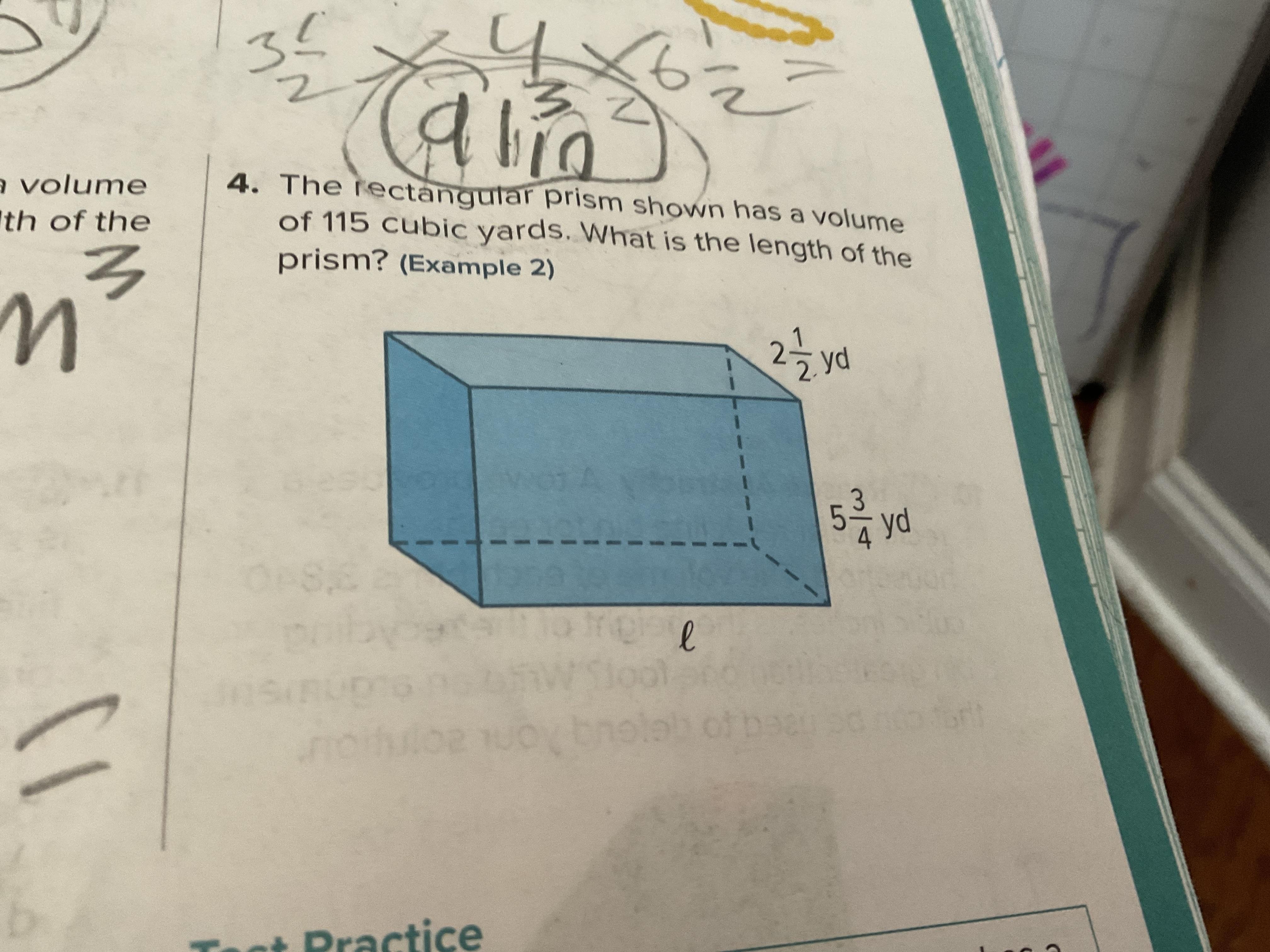
Answers
Answer: The length is 8 yards
Step-by-step explanation: First, take the volume of the prism (115 cubic yards), divide it by the width (2 1/2), the divide that by the height (5 3/4) getting you the length: 8 yards
Tolong bantuin pakai cara

Answers
Answer:
1364
Step-by-step explanation:
1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364
a1+a2 = a3, a2+a3=a4 etcetera..
1+3 =4
3+4 =7
4+7=11
.
.
a13+a14 = a15
521+843 = 1364
so, 1364 is the answer
The ages of people visiting a senior center one afternoon are recorded in the line plot
Does the data contain an outlier? If so, explain its meaning in this situation.
A: No, there is no outlier. This means that the data was not collected correctly, as there would be lots of age ranges at the center.
B: No, there is no outlier. This means that the people at the center were all seniors around the same age.
C: Yes, there is an outlier of 85. This means that one person was age 85, which is 15 years older than the next closest age.
D: Yes, there is an outlier of 105. This means that someone at the center is 105 years old.

Answers
Answer:
b
Step-by-step explanation:
The correct option is (b) The data does not contain an outlier. This means that the people at the center were all seniors around the same age.
What is an Outlier in a Dataset?Outlier in a data set is simply the extremely low data point or an extremely high data point compared to other points in the dataset.
It will stand out from the other values in the dataset.
The line plot shows the ages of people visiting a senior center one afternoon.
The data points are,
70, 70, 70, 75, 75, 80, 80, 85, 90, 90, 95, 95, 95, 100.
If there is an outlier in the set, it would be extremely low or high compared to other points.
But there are no such points.
So there are no outliers.
This means that people visited at the center were all seniors around the same age.
Hence the correct option is (b).
Learn more about Outliers here :
https://brainly.com/question/26958242
#SPJ2
Q - Determinate the value of the following expression:
\(\frac{\sqrt{36} - \sqrt[3]{8} - \sqrt{144}}{\sqrt[3]{-64} + \sqrt[3]{125} } -1\)
Answers
The value of the given expression is - 9.
The square root of a number:
The square root of a number is a value that, when multiplied by itself, gives the original number.
For example, the square root of 25 is 5, because 5 x 5 = 25.
The symbol used to denote the square root of a number is √, and it is placed in front of the number.
For example, the square root of 25 can be written as √25.
Here we have
\(\frac{ \sqrt{36} - \sqrt[3]{8} - \sqrt{144} }{\sqrt[3]{-64} \sqrt[3]{125}} - 1\)
As w know,
36 = 6 × 6 = 6²
8 = 2 × 2 × 2 = 2³
144 = 12 × 12 = 12²
-64 = - 4 × -4 × -4 = (-4)³
125 = 5 × 5 × 5 = 5³
Hence, the above expression can rewrite as follows
\(\frac{ \sqrt{36} - \sqrt[3]{8} - \sqrt{144} }{\sqrt[3]{-64}+ \sqrt[3]{125}} - 1 = \frac{ \sqrt{ 6^{2} } - \sqrt[3]{ 2^{3} } - \sqrt{12^{2} } }{\sqrt[3]{ (-4)^{2} }+ \sqrt[3]{5^{3} }} - 1\)
= \(\frac{ 6 - 2 - 12 }{ -4 + 5} - 1\)
= \(\frac{ -8 }{ 1} - 1\)
= -9
Therefore,
The value of the given expression is - 9.
Learn more about Square roots at
https://brainly.com/question/28156082
#SPJ1
Of all the soft drink consumers in a particular sales region, 30% prefer Brand A and 70% prefer Brand B. Of all these soft drink consumers, 20% prefer Brand A and are female, and 40% prefer Brand B and are female. What is the probability that a randomly selected consumer is female, given that the person prefers Brand A? A. 0.18 B. 0.21 C. 0.34 D. 0.67
Answers
Answer:
The answer to this question should be D. 0.67
Hope this helped.
For each of the 6 coverage areas of a standard homeowners insurance policy, briefly describe what they cover: Dwelling, Other Structures. Personal Property,
Loss of Use, Personal Liability, Medical Payments
Answers
Read more about homeowners insurance
brainly.com/question/30179892
#SPJ1
A cube is dilated by a scale factor of 3/4 to create a new cube.what is the surface area of the new cube
Answers
The Surface area of the new cube is 9/16 times the surface area of cube
What is an equation?An equation is an expression that shows how two numbers and variables are related using mathematical operations such as addition, subtraction, exponent, division and multiplication.
Let l represent the length of the side of the cube. Hence:
Surface area of cube = 6 * (length * length) = 6(l * l)
Surface area of cube = 6l²
The cube is dilated by a scale factor of 3/4 to create a new cube
Hence:
Length of new cube = scale factor * length = (3/4) * l = 3l/4
Surface area of new cube = 6 * (length * length) = 6(3l/4 * 3l/4)
Surface area of new cube = 6l²(9/16) = (9/16) * surface area of old cube
The Surface area of the new cube is 9/16 times the surface area of old cube
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
Consider a medium with parameters € = 1.2 (10^-10 )F/m , n= 3(10^-3) H/m and sigma=0. Magnetic field intensity in the medium is given as R = 2cos (10^10t- 600x)äz Am.
Use Maxwell's equations to obtain the followings:
1) Magnetic flux density
These questions is circuit theory
Answers
Using Maxwell's equations, we can determine the magnetic flux density. One of the Maxwell's equations is:
\(\displaystyle \nabla \times \mathbf{H} = \mathbf{J} + \frac{\partial \mathbf{D}}{\partial t}\),
where \(\displaystyle \nabla \times \mathbf{H}\) is the curl of the magnetic field intensity \(\displaystyle \mathbf{H}\), \(\displaystyle \mathbf{J}\) is the current density, and \(\displaystyle \frac{\partial \mathbf{D}}{\partial t}\) is the time derivative of the electric displacement \(\displaystyle \mathbf{D}\).
In this problem, there is no current density (\(\displaystyle \mathbf{J} =0\)) and no time-varying electric displacement (\(\displaystyle \frac{\partial \mathbf{D}}{\partial t} =0\)). Therefore, the equation simplifies to:
\(\displaystyle \nabla \times \mathbf{H} =0\).
Taking the curl of the given magnetic field intensity \(\displaystyle \mathbf{R} =2\cos( 10^{10} t-600x)\hat{a}_{z}\, \text{Am}\):
\(\displaystyle \nabla \times \mathbf{R} =\nabla \times ( 2\cos( 10^{10} t-600x)\hat{a}_{z}) \, \text{Am}\).
Using the curl identity and applying the chain rule, we can expand the expression:
\(\displaystyle \nabla \times \mathbf{R} =\left( \frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial y} -\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial z}\right) \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Since the magnetic field intensity \(\displaystyle \mathbf{R}\) is not dependent on \(\displaystyle y\) or \(\displaystyle z\), the partial derivatives with respect to \(\displaystyle y\) and \(\displaystyle z\) are zero. Therefore, the expression further simplifies to:
\(\displaystyle \nabla \times \mathbf{R} =-\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial x} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Differentiating the cosine function with respect to \(\displaystyle x\):
\(\displaystyle \nabla \times \mathbf{R} =-2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Setting this expression equal to zero according to \(\displaystyle \nabla \times \mathbf{H} =0\):
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z =0\).
Since the equation should hold for any arbitrary values of \(\displaystyle \mathrm{d} x\), \(\displaystyle \mathrm{d} y\), and \(\displaystyle \mathrm{d} z\), we can equate the coefficient of each term to zero:
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x) =0\).
Simplifying the equation:
\(\displaystyle \sin( 10^{10} t-600x) =0\).
The sine function is equal to zero at certain values of \(\displaystyle ( 10^{10} t-600x) \):
\(\displaystyle 10^{10} t-600x =n\pi\),
where \(\displaystyle n\) is an integer. Rearranging the equation:
\(\displaystyle x =\frac{ 10^{10} t-n\pi }{600}\).
The equation provides a relationship between \(\displaystyle x\) and \(\displaystyle t\), indicating that the magnetic field intensity is constant along lines of constant \(\displaystyle x\) and \(\displaystyle t\). Therefore, the magnetic field intensity is uniform in the given medium.
Since the magnetic flux density \(\displaystyle B\) is related to the magnetic field intensity \(\displaystyle H\) through the equation \(\displaystyle B =\mu H\), where \(\displaystyle \mu\) is the permeability of the medium, we can conclude that the magnetic flux density is also uniform in the medium.
Thus, the correct expression for the magnetic flux density in the given medium is:
\(\displaystyle B =6\cos( 10^{10} t-600x)\hat{a}_{z}\).
What is the average rate of change for this quadratic
function for the interval from x=2 to x = 4?
A. 12
B. -6
C. -12
D. 6
-10-
Click here for long description
SUBMIT
Answers
The average rate of change of the function over the interval is -6
Finding the average rate of changeFrom the question, we have the following parameters that can be used in our computation:
The graph
The interval is given as
From x = 2 to x = 4
The function is a quadratic function
This means that it does not have a constant average rate of change
So, we have
f(2) = -3
f(4) = -15
Next, we have
Rate = (-15 + 3)/(4 - 2)
Evaluate
Rate = -6
Hence, the rate is -6
Read more about average rate of change at
brainly.com/question/17131025
#SPJ1

Find the distance between point P and line L

Answers
The distance between point P and line L is 16/9√(13).
To find the distance between point P and line L, we can use the formula for the distance between a point and a line in two-dimensional space. The formula is as follows:
Let P = (x1, y1) be the point and L be the line ax + by + c = 0. Then the distance between P and L is:
|ax1 + by1 + c|/√(a² + b²)
To find a, b, and c for the given line, we need to put it in slope-intercept form y = mx + b by solving for y.
2x - 3y = 12=> 2x - 12 = 3y=> (2/3)x - 4 = y
The slope of the line, m, is the coefficient of x, which is 2/3. Therefore, the line is:
y = (2/3)x - 4The values of a, b, and c are: a = 2/3b = -1c = -4
Now we can substitute the coordinates of P and the values of a, b, and c into the formula for the distance between a point and a line.
Let P = (3, 5).|a(3) + b(5) + c|/√(a² + b²)= |(2/3)(3) - 1(5) - 4|/√[(2/3)² + (-1)²]= |-4/3 - 4|/√(4/9 + 1)= 16/9√(13).
for such more questions on distance
https://brainly.com/question/30395212
#SPJ8
3^6/3^10 x 3^1
Help plz
Answers
Answer:
1/27 if that's what u want
Step-by-step explanation:
How to solve your problem
3
6
3
1
0
⋅
3
1
\frac{3^{6}}{3^{10}} \cdot 3^{1}
31036⋅31
Solve
1
Evaluate the exponent
3
6
3
1
0
⋅
3
1
\frac{{\color{#c92786}{3^{6}}}}{3^{10}} \cdot 3^{1}
31036⋅31
7
2
9
3
1
0
⋅
3
1
\frac{{\color{#c92786}{729}}}{3^{10}} \cdot 3^{1}
310729⋅31
2
Evaluate the exponent
7
2
9
3
1
0
⋅
3
1
\frac{729}{{\color{#c92786}{3^{10}}}} \cdot 3^{1}
310729⋅31
7
2
9
5
9
0
4
9
⋅
3
1
\frac{729}{{\color{#c92786}{59049}}} \cdot 3^{1}
59049729⋅31
3
Divide the numbers
7
2
9
5
9
0
4
9
⋅
3
1
{\color{#c92786}{\frac{729}{59049}}} \cdot 3^{1}
59049729⋅31
1
8
1
⋅
3
3. There are five different tables in the class and five students. Each table can be occupied by only onestudent. Their
studying year consists of 200 days. As a small prank on their teacher students would like to sit in a new way every
day, so there are no two days during their studying year such that all students are occupying the same tables.
They would like to see whether this is possible. How many ways are there for them to sit in the class?
Answers
There are 3,125 different places to sit if they don't mind sharing s desk sometimes and there are 120 different places to sit, if they all sit on separate tables.
What is Probability?It is a branch of mathematics that deals with the occurrence of a random event.
Given that there are five different tables in the class and five students
Each table can be occupied by only one student
There are 200 days of studying years.
As a small prank on their teacher students would like to sit in a new way every day, so there are no two days during their studying year such that all students are occupying the same tables.
5×4×3×2×1 = 120
There are 120 different places to sit, if they all sit on separate tables.
5×5×5×5×5 = 3,125
There are 3,125 different places to sit if they don't mind sharing s desk sometimes.
Hence, there are 120 different places to sit, if they all sit on separate tables and there are 3,125 different places to sit if they don't mind sharing s desk sometimes.
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ1
please help will give 5 stars! image is attached solve for x

Answers
The value of x in the triangle is 8.37.
We have,
Similar triangles are triangles that have the same shape but may differ in size.
The properties of similar triangles are as follows:
- Corresponding angles:
The corresponding angles of similar triangles are equal. This means that the corresponding angles at each vertex of the two triangles have the same measure.
- Corresponding sides:
The corresponding sides of similar triangles are proportional. This means that the ratio of the lengths of corresponding sides in the two triangles is the same.
Now,
There are two triangles that are similar.
So,
The ratio of corresponding sides is equal.
Now,
x/7 = 10/x
x² = 70
x = √70
x = 8.37
Thus,
The value of x in the triangle is 8.37.
Learn more about triangles here:
https://brainly.com/question/25950519
#SPJ1
On 1 April mazibane has R540, 00 in his credit card account. He buys a lounge suit for R8300, 00 on credit. There is no interest on the debit amount for the first month. Thereafter the interest is 16% per year calculated daily but compounded monthly. On 1 June Mazibane pays R5000 into the account.
How much must Mazibane pay into the account on 30 June to have no debt in the account
Answers
According to the information, we can infer that Mazibane must pay R3640 into the account on 30 June to have no debt.
How to calculate the amount Mazubane must pay on 30 June?To calculate the amount Mazibane must pay on 30 June to have no debt in the account, we need to consider the initial debt, the interest, and the previous payment.
Initial Debt:
On 1 April, Mazibane had a credit card debt of R8300.Interest Calculation:
The interest on the debt is 16% per year, calculated daily but compounded monthly. From 1 April to 1 June, a period of two months, there is no interest charged on the debt.Previous Payment:
On 1 June, Mazibane paid R5000 into the account.To determine the remaining debt on 1 June, we subtract the payment from the initial debt:
Remaining debt on 1 June = R8300 - R5000 = R3300.From 1 June to 30 June, a period of one month, interest is charged on the remaining debt.
To calculate the interest for one month, we use the formula:
Interest = Principal x (1 + (rate/100))^(time/12) - Principal,where the principal is the remaining debt, the rate is the monthly interest rate (16%/12), and the time is the number of months (1).
Interest for one month = R3300 x (1 + (16/100)/12)^(1/12) - R3300.To find the total debt on 30 June, we add the remaining debt on 1 June and the interest for one month:
Total debt on 30 June = R3300 + Interest for one month.To have no debt on 30 June, Mazibane must pay the total debt amount:
Mazibane must pay R3300 + Interest for one month on 30 June.Calculating the interest and summing up the values, we find that Mazibane must pay approximately R3640 into the account on 30 June to have no debt.
Learn more about debt in: https://brainly.com/question/31792485
#SPJ1
In ΔDEF, if DE ≅ DF and EF is the hypotenuse, then ΔDEF is
a acute and scalene. c. right and isosceles.
b right and scalene. d. obtuse and isosceles.
Answers
Answer:
C. Right and isosceles
Explanation:
Since two sides of the triangle are equal in length (\(DE\) and \(DF\)), this means that the triangle is an isosceles triangle. Since \(EF\) is the hypotenuse of this triangle, it also means that the triangle is a right-angle triangle (the hypotenuse refers to the longest side of a right triangle). Therefore, we can conclude that ΔDEF is right and isosceles.
Hope this helps :)
Answer:
It is C.
Step-by-step explanation:
Hope this helped have an amazing day!
Ed decided to build a storage box. At first, he was planning to build a cubical box with edges of length n inches. To increase the amount of storage, he decided to make the box 1 inch taller and 2 inches longer while keeping its depth at n inches. The volume of the box Ed built has a volume how many cubic inches greater than the box he originally planned to build?
Answers
Answer:
The new volume is 3n^2+2n inches greater.
Step-by-step explanation:
Volume of a cube = s^3 where s is side of cube
Original volume = n^3
Volume of a Rectangular Prism = LBH
New Volume = (n+1)(n+2)(n)= n^3+3n^2+2n
DIfference = New- original = 3n^2+2n
What fraction equals 4
Answers
Here are a few 4/1 , 8/2 , 12/3
4, 8/2, 12/3 are equal to 4, when simplified, which means they are equivalent in nature.
What is fraction?A fraction is defined as numerical representation for part of a whole which represents a rational number.
If the denominator is 1, the numerator can be taken as 4, so the fraction would become \(\frac{4}{1}\) = 4
If the denominator is 2, the numerator can be taken as 8, so the fraction would become \(\frac{8}{2}\) = 4
If the denominator is 3, the numerator can be taken as 12, so the fraction would become \(\frac{12}{3}\) = 4
Thus, 4, 8/2, 12/3 are equal to 4, when simplified, which means they are equivalent in nature.
Learn more about fraction
https://brainly.com/question/10354322
#SPJ2
The area of a rectangle is 5/6 sq foot. The width is 2/3 foot. The length of the rectangle is how many feet
Answers
Answer:
The answer is
\( \frac{5}{4} \\ \)
Step-by-step explanation:
Area of a rectangle = length × width
Since we are finding the length
\(length = \frac{area}{width} \\ \)From the question
area = 5/6 sq. feet
width = 2/3 foot
Substitute the values into the above formula and solve for the length
The length is
\(length = \frac{5}{6} \div \frac{2}{3} \\ = \frac{5}{6} \times \frac{3}{2} \\ = \frac{5}{2} \times \frac{1}{2} \\ = \frac{5}{4} \)
We have the final answer as
\( \frac{5}{4} \\ \)
Hope this helps you
Answer:
5/4
Step-by-step explanation:
5/6 ÷ 2/3
5/6 * 3/2
15/12
5/4
Best of Luck!
make e the subject
e-5=2f
Answers
Answer:
e-5=2f
take '-5' to the other side where '2f' is
e=2f+5
Which of the following types of statements can justify the steps of a proof?
Check all that apply.
A. Corollaries
B. Definitions
C. Postulates
D. Conjectures
Answers
The correct options are A .Corollaries, B. Definitions, and C. Postulates. Conjectures are not used to justify the steps of a proof as they are statements that have yet to be proven.
The types of statements that can justify the steps of a proof are:
A. Corollaries
B. Definitions
C. Postulates
These three types of statements provide valid and reliable justifications when constructing a proof. Corollaries are theorems that are derived from other theorems, definitions provide clarity and context for terms used in the proof, and postulates are axioms or statements assumed to be true without proof.
D. Conjectures, however, are not reliable justifications for a proof, as they are propositions that are believed to be true but have not yet been proven.
for such more question on statements
https://brainly.com/question/13063358
#SPJ11
-12(5/6a-7/8)+1/14(3 1/2a-1 2/5)
Answers
First change mixed fractions to be full fractions
-12(5/6 a -7/8) + 1/14 (7/2 a - 7/5)
Now multiply out
-12(5)/6 a -12(-7)/8) + 7/14(2) a -7/14(5)
-60/6 a + 84/8 + 7/28 a -7/70
-10a + 10.5 + 1/4a - 1/10
-10a + 0.25a +10.5 -0.1
-9.75a + 10.4
*if this =0 and you need to solve for a then
9.75a=10.4
a= 10.4/9.75
a=16/15
In the diagram below, circle O has a radius of 10. If the measure of arc AB is 72°, find the area of shaded sector AOB, in terms of π. Show all your work that leads to the final answer.

Answers
Answer:
62.8
Step-by-step explanation:
Area of sector=(pi*r^2)*(theta/360)
Area of sector=(pi*100)*(72/360)=62.8
The area of the shaded sector AOB in terms of π is 20π units squared.
How to find area of a sector?
The area of a sector can be described as follows;
area of sector = ∅ / 360 × πr²
where
r = radius of the circleTherefore,
r = 10 units
∅ = 72°
Hence,
area of the sector = 72° / 360° × π10²
area of the sector = 7200 / 360 π
area of the sector = 20π units²
learn more on sector here: https://brainly.com/question/24351015
#SPJ2
Pairs of shorts had a mark_up of 17%which includes profit and GST at a price of k29. 25.Find the cost price.
Answers
The cost price of the shorts is K22.50.
To find the cost price of the shorts, we need to reverse calculate the original price before the markup and taxes were applied.
Let's assume the cost price of the shorts is represented by C.
The markup of 17% is applied to the cost price, which means the selling price (including the markup) is 117% of the cost price.
117% of the cost price C can be calculated as (117/100) * C.
GST (Goods and Services Tax) is also included in the selling price. GST is typically calculated as a percentage of the selling price. In this case, the selling price of the shorts including GST is K29.25.
Since the GST is included in the selling price, we can subtract it from the selling price to obtain the selling price before GST.
Let's assume the GST rate is R% (as a decimal), then the selling price before GST can be calculated as:
Selling price before GST = Selling price - (Selling price × R)
In this case, the selling price before GST is K29.25, and the GST rate is 17% (0.17 as a decimal). Substituting these values into the equation, we have:
K29.25 = Selling price - (Selling price × 0.17)
Simplifying the equation
K29.25 = Selling price × (1 - 0.17)
K29.25 = Selling price × 0.83
Selling price = K29.25 / 0.83
Now we can substitute the selling price in terms of the cost price:
K29.25 / 0.83 = (117/100) × C
Simplifying the equation:
C = (K29.25 / 0.83) × (100/117)
Calculating the cost price C:
C = K22.50
Therefore, the cost price of the shorts is K22.50.
for such more question on cost price
https://brainly.com/question/25799822
#SPJ11
help me solve this queston

Answers
TJohn's age is approximately 23.33 years, and Sharon's age is approximately 93.33 years.
And the correct graph is D.
To represent the given problem as a system of equations, we can use the following information:
John is 70 years younger than Sharon: j = s - 70
Sharon is 4 times as old as John: s = 4j
Let's plot the graph for this system of equations:
First, let's solve equation (2) for s:
s = 4j
Now substitute this value of s in equation (1):
j = s - 70
j = 4j - 70
3j = 70
j = 70/3
Substitute the value of j back into equation (2) to find s:
s = 4j
s = 4(70/3)
s = 280/3
The solution to the system of equations is j = 70/3 and s = 280/3
In the graph d, the solution to the system of equations is represented by the point (70/3, 280/3), which is approximately (23.33, 93.33) on the graph.
Therefore, John's age is approximately 23.33 years, and Sharon's age is approximately 93.33 years.
And the correct graph is D.
Learn more about system of equations click;
https://brainly.com/question/20067450
#SPJ1

Ja’Miya needs to save $84. She has saved $63. What percent of the money she needs , has she saved
Answers
Answer:
75%
Step-by-step explanation:
63/84 = .75
.75= 75%
does x = y - 2/9 show direct variation
Answers
The equation:
x = y - 2/9
Does not show a direct variation.
Does that equation show a direct variation?A direct variation between two variables x and y can be written as:
y = k*x
Where k is a constant and it is called the constant of proportionality.
In this case, the given equation is:
x = y - 2/9
We can rewrite that as:
y = x + 2/9
Where you can see we have a constant term equal to 2/9, so no, this is not a direct variation, as in the direct variation there is no constant term.
Learn more about direct variations:
https://brainly.com/question/6499629
#SPJ1
Harry and Tim both made New Year’s Resolution. Harry made 5 more resolutions than Tim. Together they made 13 resolutions. How many resolutions did Harry make?
Answers
Answer:
Harry made 9 resolutions.
Step-by-step explanation:
Tim made x resolutions.
Harry made five more, x + 5.
Harry and Tim's together was 13.
x + x + 5 = 13
combine like terms.
2x + 5 = 13
subtract 5
2x = 8
divide by 2
x = 4
Tim made 4 resolutions.
Harry made 4 + 5, that is, 9 resolutions.
Check:
Harry and Tim together is 13.
4 + 9 = 13
Harry made 9 resolutions.