in what direction did he walk during the second portion of the trip? enter the angle in degrees where negative indicates north of west and positive indicates south of west.
Answers
Orville should walk at an angle of 71.05 degrees north of west during the second portion of the trip.
When Orville walks in the northeast direction of the starting point, his angle from the east direction is 45 degrees. So, the position vector of Orville in the northeast direction will be as follows.
r = [(0.330km)cos 45° ] i+ [(0.330km)sin45°] j
r = (0.233km)i + (0.233km)j
Write the expression for the net position vector and substitute the required values to determine the value of the position vector of Orville in the second portion of the trip.
\(r = r_1+r_2\)
(0.233km)i + (0.233km)j = (0.313km) i + \(r_2\)
\(r_2\) = (0.233km)i + (0.233km)j - (0.313km) i
\(r_2\) = - (0.080km) i + (0.233 km) j
Determine the direction of Orville in the second portion of the trip.
\(tan\theta=\frac{0.233km}{-0.080km}\)
\(\theta=tan^-^1(\frac{0.233km}{-0.080km})\)
θ = -71.05°
θ = 71.05° (north of west)
So, Orville should walk at an angle of 71.05 degrees north of west during the second portion of the trip.
Learn more about Angle at:
https://brainly.com/question/31818999
#SPJ4
The given question is incomplete, complete question is:
Orville walks 0.313 km due east. He then continues walking along a straight line, but in a different direction, and stops 0.330 km northeast of his starting point.
In what direction did he walk during the second portion of the trip? Enter the angle in degrees where negative indicates north of west and positive indicates south of west.
Related Questions
The graph of a certain quadratic function has no x-intercepts. Which of the
following are possible values for the discriminant? Check all that apply.
A. 25
B. -18
C. -4
D. 0
Answers
Answer:
Step-by-step explanation:
Your answers are -18 and -4

What is the equation of the slant asymptote of the rational function f(x) = 4x^2+6x-1 / x+2?
Answers

Answer:
Hello,
y=4x-2
Step-by-step explanation:
1: slope.
\(\displaystyle \lim_{n \to \infty} \dfrac{f(x)}{x}\\\\= \lim_{n \to \infty} \dfrac{4x^2+6x-1)}{x(x+2)}\\\\= \lim_{n \to \infty} \dfrac{4x^2}{x^2}\\\\=\boxed{4}\\\)
2:
\(\displaystyle \lim_{n \to \infty} (f(x)-4x)\\\\= \lim_{n \to \infty} (\dfrac{4x^2+6x-1}{x+2}-4x)\\\\= \lim_{n \to \infty} (\dfrac{4x^2+6x-1-4x^2-8x}{x+2})\\\\= \lim_{n \to \infty} (\dfrac{-2x-2}{x+2})\\\\= \lim_{n \to \infty} (\dfrac{-2x}{x})\\\\=\boxed{-2}\\\)
Slant asymptote is y=4x-2
Taylor bought a watch onsale for 60% off the originalprice, and another 10% off thediscounted price. If the watchoriginally cost $82, what wasthe final sale price?
Answers
Original Cost - $82
First part: Apply the 60% off discount
Convert first the 60% into decimal form
60% ÷ 100% = 0.6
Multiply it to the original cost to determine the discount
$82 ˣ 0.6 = $49.2
Subtract the discount to the original price, to determine the discounted price.
$82 - $49.2 = $32.8
Second part:
The discounted price is now $32.8 for which we will apply another 10% discount.
Again, convert 10% into decimal
10% ÷ 100% = 0.1
Multiply it to the discounted price, to determine the second discount.
$32.8 ˣ 0.1 = $3.28
Subtract the discount to the already discounted price.
$32.8 - $3.28 = $29.52
Therefore, the final sale price of the watch is at $29.52.
help pls its algebra quick

Answers
Answer:
B
Step-by-step explanation:
Graph is positive and y intercept is on negative 2.
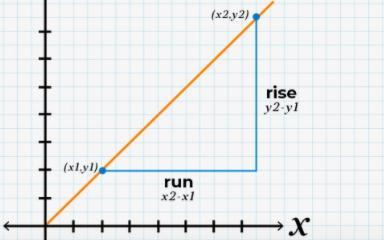
1. What is the slope and how is it determined from a g raph?
2. How do you determine the intercepts from a graph
or equation?
Answers
Answer:
The rise divided by the run is the slope of a line. The rise and run are used to estimate the slope of a line from its graph.
To determine the intercepts from a graph, We put y equal to zero and solve for x to find the x-intercept. Similarly, we put x equal to zero and solve for y to find the y-intercept.
6c + 7c +7c + 8c + 9c nesesito de su ayuda plis
Answers
Answer:
37c
Step-by-step explanation:
6c+(7c+7c)+8c+9c
6c+14c+(8c+9c)
6c+(14c+17c)
6c+31c
37c
In a local election, one candidate received 43% of the votes. Only 87 people voted in the election. Which proportion could be used to find how many votes the candidate received
Answers
we can use the proportion: (Number of votes received by the candidate) / (Total number of votes) = 43% / 100%. the candidate received approximately 37.41 votes.
In the given local election, the candidate received 43% of the votes. To determine the number of votes they obtained, we need to use a proportion. A proportion is an equation that states that two ratios are equal.
Let's represent the number of votes received by the candidate as "x." The total number of votes cast in the election is stated as 87.
We can set up the proportion:
x / 87 = 43% / 100.
To solve for "x," we can cross-multiply:
100 * x = 43% × 87.
Simplifying further, we have:
x = (43/100) × 87.
By multiplying the fraction (43/100) by 87, we can determine the number of votes received by the candidate. Evaluating this expression, the candidate received approximately 37.41 votes.
learn more about proportion here:
https://brainly.com/question/31548894
#SPJ11
Describe the shape of the distribution.
A. It is symmetric.
B. It is uniform.
C. It is bimodal.
D. It is skewed.

Answers
Which is not a function

Answers
Answer:
c
Step-by-step explanation:
it dose not have a set pattern
Answer:
a
Step-by-step explanation:
each input has to have exactly one output
In answer a the input 2 has 5 outputs
(x+2)^2=-16 This equation had no solution, why not?
Answers
Answer:
It has no solution within Real numbers. Its solutions are Complex/imaginary, since its discriminant is negative (-64).
Step-by-step explanation:
The normalized form of the equation
(x+2)^2= - 16
x^2 + 4x + 4 = - 16
x^2 + 4x + 20 = 0
We have in the form ax^2 + abx + c = 0
a = 1
b = 4
c = 20
Discriminant is b^2 - 4ac = 4^2 - 4*1*20 = 16 - 80 = - 64
Discriminant is negative, therefore, no Real solutions.
Solve x – 1 + 5 = 2
Answers
Answer:
x=8
Step-by-step explanation:
add 5+1 and you get 6. To find what minus 6 equals 2 add 2 to 6 giving you 8
Answer:
4 - 1 + 5 =2
because if 1+5 is 6 then you need to know is 6 - what is 2 and the answer is 4.
In which quadrant does 0 lie if the following statements are true:
csc 0 >0 and cos 0 <0
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
Answers
The answer is Quadrant II. First, we need to understand what csc and cos represent in trigonometry. Csc (cosecant) is the reciprocal of sine, meaning it is equal to 1/sin.
Cos (cosine) represents the ratio of the adjacent side of a right triangle to its hypotenuse.
Now, let's look at the given statements. csc 0 > 0 means that the sine of 0 is positive. Since sine is positive in Quadrants I and II, we know that 0 lies in either of those two quadrants.
Next, cos 0 < 0 means that the cosine of 0 is negative. Since cosine is negative in Quadrants II and III, we can eliminate Quadrant I as a possibility and conclude that 0 must lie in Quadrant II.
Based on the given conditions, csc θ > 0 and cos θ < 0, θ lies in Quadrant II.
Explanation:
csc θ is positive when sin θ is positive. Sin θ is positive in Quadrant I and II.
cos θ is negative in Quadrant II and III.
The only common quadrant is Quadrant II.
To know more about trigonometry visit:-
https://brainly.com/question/29002217
#SPJ11
2
A math teacher observed that as the number of hours students studied their multiplication facts increased, the
number of errors the students made on their multiplication tests decreased. Which scatterplot could support this
teacher's observation?
F
G
Number of Errors
Number of Errors
10
0
y
10
0
Multiplication Tests
12 3 4
Study Time (hours)
Multiplication Tests
1 2 3 4
Study Time (hours)
5
H
J
Number of Errors
Number of Errors
10
2
10
Multiplication Tests
2
●
0 1 2 3 4
Study Time (hours)
Multiplication Tests
●
0 1 2 3 4
Study Time (hours)
5
Answers
A scatterplot that shows the number of hours studied on the x-axis and the number of errors on the y-axis would best support the teacher's observation.
What is error in math?Error in math is an incorrect answer to a mathematical equation or problem. It can be caused by a variety of factors, such as inaccurate calculations, misreading instructions, or not understanding the problem. Error in math can be frustrating and can lead to poor grades, but it can also be an opportunity for learning and growth. With the proper guidance and understanding, students can learn from their mistakes and become better mathematicians.
The scatterplot would likely show a negative correlation, with the number of errors decreasing as the number of hours studied increases. This indicates that as students study more, their performance on multiplication tests improves. It could also show an outlier or two, which could indicate that some students are able to learn multiplication facts more quickly than others.
To know more about error click-
https://brainly.com/question/28001423
#SPJ1
Solve the following system of linear equations. x + 2y = 3 - 2x - 3y + 2z = 2y - 2x + z = 4
Answers
By using the substitution method, we conclude that the solution to the system is x = 7, y = -2, z = 2.
How to solve the system of equations?Here we have the system:
x + 2y = 3
-2x - 3y + 2z = 2y
-2x + z = 4
To solve this, first, we need to isolate one of the variables in one of the equations. We can isolate x on the first one:
x = 3 - 2y
Now we can replace that in the other two equations:
-2*( 3 - 2y) - 3y + 2z = 2y
-2*( 3 - 2y) + z = 4
Now we simplify these two:
-6 - y + 2z = 0
-6 - 4y + z = 4
Now we can isolate z on the second equation:
z = 4 + 4y + 6 = 4y + 10
And replace it on the other equation:
-6 - y + 2*(10+ 4y ) = 0
-6 - y + 20 + 8y = 0
7y + 14 = 0
y = -14/7 = -2
Now that we know the value of y, we can find the values of x and z.
z = 4y + 10 = 4*(-2) + 10 = 2
x = x = 3 - 2y = 3 - 2*(-2) = 7
So the solution is:
x = 7, y = -2, z = 2.
If you want to learn more about systems of equations:
https://brainly.com/question/13729904
#SPJ1
Martin painted 255 square feet of this
kitchen wall with į gallon of paint. If
he continues coverage at the same
rate, how many square feet can he
cover with 2 gallons of paint?
A 765 ft2
B 510 ft2
© 382.5 ft2
D 1,020 ft
Answers
Answer:
i dont know
Step-by-step explanation:
Please explain these sub headings in detail as possible . Minimum 7 pages.
3. Mathematics Modelling of Surfaces
• Discuss the term 'surface', in the context of Digital Terrain Modelling
Discuss the difference between '3D' and '2%D' Digital Terrain Models
Answers
Mathematical modeling of surfaces is the representation of two-dimensional manifolds using mathematical techniques, particularly in the context of Digital Terrain Modeling (DTM) where surfaces refer to the Earth's terrain or physical objects.
Mathematical modeling of surfaces plays a crucial role in various fields, including computer graphics, engineering, and geosciences. Surfaces are fundamental objects that can be represented and analyzed using mathematical techniques.
In this section, we will delve into the concept of surfaces, particularly in the context of Digital Terrain Modeling (DTM). Additionally, we will explore the distinction between 3D and 2D DTM.
1. The Concept of Surfaces:
In the realm of mathematics, a surface is defined as a two-dimensional manifold, meaning it is a topological space that locally resembles Euclidean space.
In simpler terms, a surface is a geometrical entity that can be thought of as a continuous collection of points, forming a boundary between a solid and its surrounding space. In the context of DTM, surfaces typically refer to the representation of the Earth's terrain or any other physical object using mathematical models.
2. Digital Terrain Modeling:
Digital Terrain Modeling involves the creation of digital representations of the Earth's surface or any specific region using computer algorithms. It serves as a crucial tool in various applications, such as urban planning, environmental analysis, and military simulations. DTM utilizes mathematical models to represent the terrain accurately, allowing for detailed analysis and visualization.
3. 3D Digital Terrain Models:
A 3D Digital Terrain Model (DTM) is a representation of the Earth's surface that captures three-dimensional information. It provides a detailed depiction of the terrain, including elevation data, contours, and topographical features.
3D DTMs are typically generated using techniques such as LiDAR (Light Detection and Ranging) or photogrammetry. These models enable precise analysis of the landscape, volumetric calculations, and visualization from different perspectives.
4. 2D Digital Terrain Models:
In contrast to 3D DTMs, 2D Digital Terrain Models represent the Earth's surface in two dimensions. They provide a simplified view of the terrain, focusing primarily on elevation data and contour lines. 2D DTMs are commonly used in cartography, where the terrain is represented on a flat surface, such as a map or a computer screen. While they lack the depth information of 3D DTMs, 2D models are still valuable for many applications, including geographic information systems (GIS) and land surveying.
5. Differences between 3D and 2D Digital Terrain Models:
The main distinction between 3D and 2D DTMs lies in the level of detail and the dimensionality of the representation. 3D DTMs provide a more comprehensive and realistic view of the terrain, capturing not only the elevation but also the shape, slopes, and other three-dimensional features. These models are highly suitable for applications that require a precise understanding of the terrain's topography, such as hydrological analysis or landscape design.
On the other hand, 2D DTMs offer a simplified representation of the terrain, primarily focusing on elevation data and contour lines. They are more commonly used for general visualization and analysis purposes where the third dimension is not critical. 2D DTMs are easier to create and process, making them more accessible for applications that do not require intricate three-dimensional modeling.
To know more about Mathematical modeling refer here:
https://brainly.com/question/10952874#
#SPJ11
The volume of a sphere is V = 4/3 pi r³
and the relationship between d the radius r and the diameter d is r = d/2.
Find the volume of the sphere in terms of the diameter d and simplify the expressions.
What is the volume of the sphere when the diameter is 2/3 centimeter?
Answers
V = (4/3) x π x (d/2)^3
Simplifying the expression inside the parentheses:
(d/2)^3 = d^3/8
Substituting again:
V = (4/3) x π x (d^3/8)
Simplifying:
V = π x d^3/6
When the diameter is 2/3 centimeter, we have:
V = π x (2/3)^3/6
V = π x 8/162
V = 4π/81 cubic centimeters (in terms of π)
Or approximately:
V ≈ 0.0524 cubic centimeters (rounded to four decimal places)
one followed by twelve zeros
Answers
Answer:
Trillion is a 1 with 12 zeros after it, and it looks like this: 1,000,000,000,000.
Step-by-step explanation:
Answer:
1000000000000
quadrillions
Step-by-step explanation:
Russell runs 9/10 mile in 5 minutes. At the rate, how many miles can he run in one minute
Answers
9/10 mile = 5 min
9/10 ÷ 5 mile = 1 min
9/10 × 1/5 mile = 1 min
9/50 mile = 1 min
R is partly constant and partly varies with E, when R=530,E=1600 and when R=730,E=3600
Find the formular which connects R and E
Find R when E=1300
Answers
Hi there!
Please check the answer of the image attached for explanation.
Hope this helps....

The value of R at E = 1300 is 500 and the Equation that satisfies R and E is 10R = E + 3700.
What is a linear equation?
Because a straight line emerges when we attempt to display the graph of the provided linear function, a linear equation is known as linear.
Given, R is partly constant and partly varies with E, when R=530, E=1600, and when R=730, E=3600
Since R is partly constant and partly depends on E.
Let b Be the constant part of R and a be the part of R that varies with E
Thus,
R = a * E + b...(1)
Given at E is equal to 1600 R is 530 and at E is 3600 R is 730
Substituting these values in equation 1
530 = 1600a + b......(2)
730 = 3600a + b........(3)
From comparing equation 2 and equation 3
2000a = 200
a = 1/10
from equation 2
b = 370
Thus, the equation in R and E:
R = 1/10 E + 370
=> 10R = E + 3700
Value of R at E = 1300
R = 130 + 370
r = 500
Therefore, the Equation that satisfies R and E is 10R = E + 3700.
Learn more about linear equations here:
https://brainly.com/question/11897796
#SPJ2
what types of solutions does this equation have?

Answers
Answer:
Two imaginary solutions.
Step-by-step explanation:
In order to simplify the equation, we square root both sides. As the argument (value in the root) is negative, and we know that the square root function's domain is only positive numbers, we would have two imaginary solutions.
This would be positive/negative \(3i\sqrt{5}\).
Another way to visualize this is by looking at the parabola's graph. Through algebraic manipulation, we know that the parabola is z^2 + 45. This parabola never crosses the x-axis. Therefore there are two solutions that are imaginary.
I hope this helps!
a boat is pulled into a dock by means of a rope attached to a pulley on the dock. the rope is attached to the front of the boat, which is 7 feet below the level of the pulley. if the rope is pulled through the pulley at a rate of 12 ft/min, at what rate will the boat be approaching the dock when 120 ft of rope is out?
Answers
The rate of boat be approaching the dock when 120 ft of rope is out is 12 ft/ sec.
What is meant by the Pythagorean theorem?A theorem stating that square of the length of a right triangle's hypotenuse equals the total of the squares of the other sides. The formula is c2 = a2 + b2, in which c is the length of a hypotenuse and a and b are the lengths of the remaining two sides.For the given question.
The rate of pulling the pulley is 12 ft/min.
The distance of the rope with the boat is 7 feet.
The rope given by the hypotenuse.
y = 7 is constant.
Let H be the total height that is hypotenuse.
Le 'x' be the depth of dock approaching.
Using Pythagorean theorem.
H(t) = √(49 + x²)
Differentiate the height with respect to time.
dH/dt = (x) / √(49 + x²) dx/dt
Put the values. x = 120 ft.
12 = 120/ √(120² + 49)dx/dt
12 = 120/ √(14449) (dx/dt)
12×√(14449)/120 = dx/dt
dx/dt = 12 ft/ sec.
Thus, the rate of boat be approaching the dock when 120 ft of rope is out is 12 ft/ sec.
To know more about the Pythagorean theorem, here
https://brainly.com/question/343682
#SPJ4
The height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is 1/(a-b). True False
Answers
The statement "The height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is 1/(a-b)" is False.
In a uniform distribution, the probability density function (PDF) is constant within the interval [a, b]. The height of the PDF represents the density of the probability distribution at any given point within the interval. Since the PDF is constant, the height remains the same throughout the interval.
To determine the height of the PDF, we need to consider the interval length. In a uniform distribution defined on the interval [a, b], the height of the PDF is 1/(b - a) for the PDF to integrate to 1 over the entire interval. This means that the total area under the PDF curve is equal to 1, representing the total probability within the interval [a, b].
Therefore, the correct statement is that the height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is not 1/(a - b), but rather it is a constant value necessary for the PDF to integrate to 1 over the interval, i.e., 1/(b - a).
Learn more about uniform distribution here:
https://brainly.com/question/32291215
#SPJ11
OnOff
Question
A composite figure is shown.
What is the total area of this figure?
164 sq. cm.
136 sq. cm.
216 sq. cm.
160 sq. cm.

Answers
Answer:
164 cm^2
Step-by-step explanation:
lets find square of triangle first
corner ABD is 90 degrees coz corner ABC is 180 degrees and EBC is 90
(sum of all angles of a quadrilateral is 360,
B = 360 - C - F - E
360 - 90 - 90 - 90 = 90)
BD = CF - DE
BD = 16 - 8 = 8 cm
S ABD = AB * BD / 2 (coz corner B is 90 degrees)
S ABD = 13 * 8 / 2 = 13 * 4 = 52 cm^2
lets find square of BEFC next
S BEFC = CF * EF ( B = C = F = E = 90 so thats a rectangle)
S BEFC = 16 * 7 = 70 + 42 = 112 cm^2
finally lets find total area
S = S ABD + S BEFC = 52 + 112 = 164 cm^2
Solve y = x + 8 for x.
A x = y + 8
B x = y − 8
C x = −y + 8
D x = −y − 8
Answers
Answer:
chess is good oodles like poodles
Which expression is equivalent to 3(6+p) ?
Answers
Answer:
18 + 3p
Step-by-step explanation:
Using distributive property:
3(6+p)
18 + 3p
What is the unit rate of (0,0) (6,8)
Answers
Answer:
4/3.
Step-by-step explanation:
Unit rate is the same as slope. In order to find the slope, we are going to use this formula:
m = y2 - y1 / x2 - x1
Now, we substitute the numbers into the equation:
m = 8 - 0 / 6 - 0
m = 8/6
m = 4/3
Therefore, the unit rate is 4/3.
Write two equations-one in logarithmic form and one in exponential form-that represent the
statement: "the natural logarithm of 10 is y".
Answers
Expressions can be expressed in logarithmic forms, and in exponential forms
The two equations are \(\ln(10) = y\) and \(10 = e^y\)
How to determine the expressions.The statement is given as "the natural logarithm of 10 is y".
The logarithmic expression of the above statement is:
\(\ln(10) = y\)
Rewrite the above expression, as an exponential equation
\(10 = e^y\)
Hence, the two equations are \(\ln(10) = y\) and \(10 = e^y\)
Read more about logarithms at:
https://brainly.com/question/1832186
Can the terms susc as "less than" and "more than" be used in a real situation? Can you give an example or examples?
Answers
Answer:
Yes
Step-by-step explanation:
She had more than me
I would help her but she has less than me
forestry ranger is in a stand 200 feet in the air. There is an angle of
depression of 35 degrees to a campfire. How far is it from the base of the
stand to the campfire?
Answers
the distance from the base of the stand to the campfire is 285.6 feet.
The angle of depression of 35 degrees.
Let's denote the distance from the base of the stand to the campfire as "x."
Using the tangent function, we have:
tan(35 degrees) = opposite/adjacent
tan(35 degrees) = 200/x
To find the value of x, we can rearrange the equation:
x = 200 / tan(35 degrees)
x ≈ 200 / 0.7002
x ≈ 285.6 feet
Therefore, the distance from the base of the stand to the campfire is 285.6 feet.
Learn more about Trigonometry here:
https://brainly.com/question/12068045
#SPJ1