In the diagram below, fg is parallel to CD, if CE = 32, FE = 20 and CD = 16 find the length of FG . Figures are not necessarily drawn to scale.

Answers
The length of FG is 40 units.
What are parallel lines?
Two or more lines that are consistently parallel to one another and that are located on the same plane are referred to as parallel lines. No matter how far apart parallel lines are, they never cross. The relationship between parallel and intersecting lines is the reverse. The lines that never meet or have any possibility of meeting are known as parallel lines.
Since FG is parallel to CD, triangles CDE and FGE are similar. Thus, we can set up the following proportion:
CE/CD = FG/FE
Substituting the given values, we get:
32/16 = FG/20
Simplifying the left side, we get:
2 = FG/20
Multiplying both sides by 20, we get:
FG = 40
Therefore, the length of FG is 40 units.
Learn more about parallel lines on:
https://brainly.com/question/964336
#SPJ1
Related Questions
Two points A (-2, 9) and B (4, 8) lie on a line l. (i) Find the slope of the line l. (2)marks (ii) Find the coordinates of the midpoint of the points A and B (iii) Find the distance between points A and B. (i). A line “t” is parallel to 3y = 6x + 9. Find the slope of this line “t”. (ii) Another line “r” is perpendicular to the line 3y = 6x + 9. Find the gradient of the line “r”.
Answers
Answer:
Question 1:
The coordinates are A(-2,9) and B(4,8)
(i) Slope = \(\frac{rise}{run}\)
Slope = \(\frac{y2-y1}{x2-x1}\)
Slope = \(\frac{8-9}{4+2}\)
Slope = \(\frac{-1}{6}\)
(ii) M(x,y) = \((\frac{x1+x2}{2} , \frac{y1+y2}{2} )\)
=> M(x,y) = \((\frac{-2+4}{2}, \frac{9+8}{2})\)
=> M(x,y) = \((\frac{2}{2} , \frac{17}{2} )\)
=> M(x+y) = (1 , 8.5)
(iii) Distance Formula = \(\sqrt{(x2-x1)^2+(y2-y1)^2}\)
D = \(\sqrt{(4+2)^2+(8-9)^2}\)
D = \(\sqrt{(6)^2+(-1)^2}\)
D = \(\sqrt{36+1}\)
D = \(\sqrt{37 }\) units
Question 2:
(i) The given equation is:
=> 3y = 6x+9
=> 3y = 3(2x+3)
Dividing both sides by 3
=> y = 2x+3
Where Slope = m = 2 and y-intercept = b = 3
Parallel lines have equal slopes
=> So, Slope of line "t" = 2
(ii) Line 3y = 6x+9 has a slope of 2
=> Perpendicular lines have a slope of negative reciprocal such that multiplying their slopes will give -1
=> Gradient of line "r" = -1/2
If f(a)=-5, what is the value of |f(a)|?
Answers
|f(a)| , the vertical lines mean absolute value. Absolute value is the positive value of the answer whether it is actually negative or positive.
F(a) is given as -5, so the absolute answer would be 5
The answer is 5
What is the function graphed below?
y = | x - 1|
y = | x | - 1
y = | x + 1|
y = | x | + 1
Answers
The function represented by the graph is y = |x + 1|
How to determine the function of the graphThe complete question is added as an attachment
From the question, we have the following parameters that can be used in our computation:
The equation of the graph is an absolute value graph
An absolute value graph is represented as
y = |x|
The function is shifted left by 1 units
So, we have
y = |x + 1|
Hence, the function is y = |x + 1|
Read more about transformation at
https://brainly.com/question/1548871
#SPJ1

Find the distance traveled by a particle with position (x, y) as t varies in the given time interval.
x = 4 sin^2(t), y = 4 cos^2(t), 0 ≤ t ≤ 5π
What is the length of the curve?
Answers
Hence, the length of the curve defined by the parametric equations x = 4sin^2(t) and y = 4cos^2(t) over the interval 0 ≤ t ≤ 5π is 20π units.
To find the distance traveled by the particle, we need to calculate the length of the curve defined by the parametric equations x = 4sin^2(t) and y = 4cos^2(t) over the given time interval 0 ≤ t ≤ 5π.
We can use the arc length formula to calculate the length of the curve. The arc length formula for a parametric curve defined by x = f(t) and y = g(t) is given by:
L = ∫[a, b] √[f'(t)^2 + g'(t)^2] dt
where f'(t) and g'(t) are the derivatives of f(t) and g(t) with respect to t.
Let's start by finding the derivatives of x and y with respect to t:
x = 4sin^2(t)
x' = d/dt(4sin^2(t))
= 8sin(t)cos(t)
= 4sin(2t)
y = 4cos^2(t)
y' = d/dt(4cos^2(t))
= -8cos(t)sin(t)
= -4sin(2t)
Now, let's calculate the length of the curve using the arc length formula:
L = ∫[0, 5π] √[x'(t)^2 + y'(t)^2] dt
= ∫[0, 5π] √[16sin^2(2t) + 16sin^2(2t)] dt
= ∫[0, 5π] √[32sin^2(2t)] dt
= ∫[0, 5π] √[32sin^2(2t)] dt
= ∫[0, 5π] 4√[2sin^2(2t)] dt
= 4∫[0, 5π] √[2sin^2(2t)] dt
= 4∫[0, 5π] √[2(1 - cos^2(2t))] dt
= 4∫[0, 5π] √[2(1 - (1 - 2sin^2(t))^2)] dt
= 4∫[0, 5π] √[2(2sin^4(t))] dt
= 4∫[0, 5π] √[8sin^4(t)] dt
= 4∫[0, 5π] 2sin^2(t) dt
= 8∫[0, 5π] sin^2(t) dt
We can use the trigonometric identity sin^2(t) = (1 - cos(2t))/2 to simplify the integral further:
L = 8∫[0, 5π] sin^2(t) dt
= 8∫[0, 5π] (1 - cos(2t))/2 dt
= 4∫[0, 5π] (1 - cos(2t)) dt
= 4∫[0, 5π] dt - 4∫[0, 5π] cos(2t) dt
The integral of dt over the interval [0, 5π] is simply the length of the interval, which is 5π - 0 = 5π. The integral of cos(2t) over the same interval is zero since the cosine function is periodic with period π.
Therefore, the length of the curve is given by:
L = 4(5π) - 4(0)
= 20π
To know more about parametric equations,
https://brainly.com/question/31399244
#SPJ11
is y=-x+2 a linear equation
Answers
Answer:
yes it is
Step-by-step explanation:
it is linear because the number can fall on both the x and y axis
Answer:
y = -x + 2 is a Linear Equation.
Step-by-step explanation:
The equation is in slope-intercept form of a linear function.
Slope-intercept form: y = mx + b ---> y = y, -x = mx, b = 2
What is the degree of the polynomial 7x³ 5x 4x³ 2x²?
Answers
The degree of the polynomial 7x³ 5x 4x³ 2x² is 3.
The degree of a polynomial is the highest power of x in the polynomial.
In this case, the polynomial is 7x³ 5x 4x³ 2x², and the highest power of x is x³. This means that the degree of this polynomial is 3.
It's important to note that when working with polynomials it's important to pay attention to the signs of the coefficients. In this case, we have 7x³, 5x, 4x³, 2x². The x³ term has the highest degree and it's coefficient is 7, the x term has the second highest degree and it's coefficient is 5, the x³ term has the same degree as the first x³ term, but the coefficient is different, and the x² term has the fourth highest degree and it's coefficient is 2.
Learn more about Polynomials here:
https://brainly.com/question/2833285
#SPJ4
x + 3y = 8
Y = 2 - x
solve for the system of equations
Answers
4/5 divided by 1/3 ??
Answers
Answer:
2.4
Step-by-step explanation:
What is the vertex of this angle?
and what are the sides?
50 points for correct answer

Answers
Sides of the angle are B and C
PLEASE I REALLY NEED HELP PLEASE!!

Answers
Answer:
I think the answer is B.
Step-by-step explanation:
(1 point) Find a particular solution to Yp= y" + 2y + y = -7e-¹ 1² + 1
Answers
To find a particular solution to the given differential equation Y_p = y'' + 2y + y = -7e^(-x) + 1^2 + 1, we can use the method of undetermined coefficients.
First, we assume that the particular solution has the form Y_p = Ae^(-x) + Bx^2 + Cx + D, where A, B, C, and D are constants to be determined.
Taking the derivatives of Y_p, we have Y_p' = -Ae^(-x) + 2Bx + C and Y_p'' = Ae^(-x) + 2B.
Substituting these derivatives into the differential equation, we get (Ae^(-x) + 2B) + 2(Ae^(-x) + Bx^2 + Cx + D) + (Ae^(-x) + Bx^2 + Cx + D) = -7e^(-x) + 1^2 + 1.
By comparing the coefficients of like terms on both sides of the equation, we can determine the values of A, B, C, and D.
Finally, substituting these values back into the particular solution equation Y_p = Ae^(-x) + Bx^2 + Cx + D gives us the particular solution to the given differential equation.
Learn more about differential equation here: brainly.com/question/25731911
#SPJ11
what’s the biggest difference between an area variance and a use variance?
Answers
The main difference between an area variance and a use variance is that area variance allows for an exception to zoning regulations related to the physical characteristics of a property, while use variance allows for an exception to regulations related to the intended use of a property.
An area variance is typically granted when a property owner is unable to comply with zoning regulations related to setbacks, building height, lot coverage, or other physical characteristics of a property.
In contrast, a use variance allows a property owner to use their property for a purpose that is not permitted under the current zoning regulations. This may include using a residential property for commercial purposes or using a commercial property for residential purposes.
Use variances are generally more difficult to obtain than area variances, as they require a showing of a unique hardship or practical difficulty that cannot be addressed through other means.
For more questions like Variance visit the link below:
https://brainly.com/question/30712824
#SPJ11
when thinking about the variability of a categorical distribution, it is sometimes useful to think of the word _______.
Answers
The variable of a categorical distribution can be described by the word "diversity", which indicates the different categories and range of outcomes.
When thinking about the variability of a categorical distribution, it is helpful to think of the word "diversity". This is because diversity describes the different categories and the range of outcomes they represent. For example, in a categorical distribution of gender, there would be two categories - male and female - and the range of outcomes would be the different percentages of each gender in the population. The variability of a categorical distribution is often important to consider, as it can inform decisions and provide important insights. For example, if a company wanted to make sure their hiring practices were fair, they might compare the gender distribution of their applicants to the gender distribution of the overall population. This would allow them to ensure they are not disproportionately hiring one gender over the other.
Learn more about variable here
brainly.com/question/29583350
#SPJ4
Solve the system below for x and y in terms of a and b.
\(ax+y=7\\3x-y=b\)
Answers
![Solve the system below for x and y in terms of a and b.[tex]ax+y=7\\3x-y=b[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/E0MzG1BcdxhYiYAQ54lED87Rwi3fUdYG.png)
What is the total surface area? Can someone please help me with this!

Answers
Answer:
the answer is 57.72 square ft
Answer:
*surface area* meaning all areas of all the sides added up.
6.5 x 5.2 = 33.8
33.8 divided by 2 = 16.9
16.9 x 2 = 33.8 (area of triangles)
5.2 x 2.4 = 12.48 (area of the bottom rectangle)
2.4 x 3.9 = 9.36 (area of the rectangle standing)
6.5 x 2.4 = 15.6 (area of the slanted rectangle)
33.8 + 12.48 + 9.36 + 15.6 = 71.24
Step-by-step explanation:
I think I got it wrong im trying to look for my mistake dont enter yet!
on the hit HGTV show Flipping the Block, Whitney and John can paint 2 walls in 30 min. At this rate, how many walls can they paint
In 1, 2, 3, and 4 hours? Graph the ordered pairs created by (hours, walls) on the coordinate plane.
Pls answer QUICKKKK!!!
Answers
Type the correct answer in the box.
Diagram shows a small square inscribed in a large square such that its vertices lie on large square sides forming 4 right triangles. One right triangle (left) base as b. The other right triangle (right) base as a, vertical leg as b, hypotenuse as c.
In the figure, a square is inside another bigger square.
If a = 4 units and b = 3 units, the length of the diagonal of the outside square rounded to the nearest tenth is
units and the length of the diagonal of the inside square rounded to the nearest tenth is
units.
Answers
The diagonal of the outside square is 9.9 units and the diagonal of the inside square is 7.1 units
Calculating the diagonal of the outside squareThe square is added as an attachment
The diagonal (d) of the outside square can be calculated using the following pythagorean theorem
d = √[2(a + b)²]
So, we have
d = √[2(4 + 3)²]
This gives
d = 9.9 units
Calculating the diagonal of the inside squareStart by calculating c using
c = √a² + b²
The diagonal (d) of the inside square can be calculated using the following pythagorean theorem
d = √[2c²]
This gives
d = c√2
So, we have
d = √[a² + b²] * √2
By substitution, we have
d = √[4² + 3²] * √2
This gives
d = 7.1 units
So, the small diagonal is 7.1 units
Read more about pythagorean theorem at
https://brainly.com/question/654982
#SPJ1

Answer:
If a = 4 units and b = 3 units, the length of the diagonal of the outside square rounded to the nearest tenth is
9.9 units and the length of the diagonal of the inside square rounded to the nearest tenth is 7.1 units.
Step-by-step explanation:
Solve each system of equations by SUBSTITUTION. Clearly identify your solution.2x + 5y = -7 7x + y = -8
Answers
The solution of the system of equations are;
⇒ x = - 1 and y = - 1
What is substitution method?
To find the value of any one of the variables from one equation in terms of the other variable is called the substitution method.
Given that;
The system of equation is,
⇒ 2x + 5y = - 7
⇒ 7x + y = - 8
Now,
Solve the system of equation as;
⇒ 2x + 5y = - 7 ... (i)
⇒ 7x + y = - 8 .. (ii)
Multiply by 5 in equation (ii) and subtract from (i), we get;
⇒ 2x + 5y - 35x - 5y = - 7 + 40
⇒ - 33x = 33
⇒ x = - 1
And, 2x + 5y = -7
⇒ 2 × -1 + 5y = -7
⇒ - 2 + 5y = - 7
⇒ 5y = - 7 + 2
⇒ 5y = - 5
⇒ y = - 1
Thus, The solution of the system of equations are;
⇒ x = - 1 and y = - 1
Learn more about the system of equation visit:
https://brainly.com/question/13729904
#SPJ1
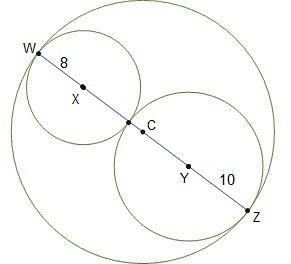
line segment wx is the radius of circle x, and line segment zy is the radius of circle y. points w, x, c, y, and z are all on line segment wz. what is the area of circle c, which passes though points w and z? 81 164 324 1296
Answers
The area of circle C, which passes though points W and Z is 324π square meters.
The center of the outer circle, Point D, is where we want to calculate the area of the circle has a WZ diameter and WC and CZ radii.
That YZ = YD = 10 cm is known.
Let DC = x and CY = 10 - x
The outer circle's radius can be expressed as 8 + 8 + x or 10 + 10 - x, which we can equate to determine its value of x
8 + 8 + x = 10 + 10 - x
Simplify
16 + x = 20 - x
Subtract 16 on both side, we get
x = 4 - x
Add x on both side, we get
2x = 4
Divide by 2 on both side, we get
x = 2
As a result, the circle's radius is
= 8 + 8 + x
= 16 + x
= 16 + 2
= 18 cm
The area of circle = πr²
The area of circle = π(18)²
The area of circle = 324π
Thus, the circle's area is 324π square meters.
To learn more about area of circle link is here
brainly.com/question/28642423
#SPJ4
The complete question is:
Line segment WX is the radius of circle X, and line segment ZY is the radius of circle Y. Points W, X, C, Y, and Z are all on line segment WZ.
What is the area of circle C, which passes though points W and Z?
A. 81
B. 164
C. 324
D. 1296
Below are sketches of histograms for three lists. (a) In scrambled order, the averages are 40, 50, 60. Match the histograms with the averages. (b) Match the histogram with the description:the median is less than the average the median is about equal to the average the median is bigger than the average (c) Is the SD of histogram (iii) around 5, 15, or 50? (d) True or false, and explain: the SD for histogram (i) is a lot smaller than that for histogram (iii).
Answers
(a) (i) 60 , (ii) 50 , (iii) 403
(b) Histogram is: (i) left-skewed , (ii) symmetric and (iii) right-skewed
(c) The SD is about 15
(d) False, their SD share about the same
(a) from the data , we can conclude that,
(i)60
(ii)50
(iii)403pts
(b)
(i) is left-skewed (long left tail)– median is greater than the average–Histogram
(ii) is symmetric – median is about equal to the average–Histogram
(iii) is right-skewed (long right tail) – median is smaller than the average3pts
(c)
The SD is about 15. Since almost all of the area is within 50 units from the average, by the 68-95% rule, 50 is too big. Very little of the data is within 5 of the average, so 5 is too small. It must be about 15.3pts
(d)
False. Histograms (i) and (iii) look almost like mirror images of each other, so their SD share about the same.
Learn more about Histogram at:
https://brainly.com/question/25983327
#SPJ1
Find the value of x. 64° 60° 36° X 48° X
Answers
Answer:
64° 60° 36° 32° 48° 44°
Step-by-step explanation:
It is subtracting by 4° each time
A man buy a houe for $175,000. He make a $75,000 down payment and amortize the ret of the debt with emiannual payment over the next 10 year. The interet rate on the debt i 12%, compounded emiannually. FInd: (a) the ize of each payment, (b) the total amount paid over the life of the loan, and (c) the total interet paid over the life of the loan
Answers
a) The size of each payment = $8718.4
b) The the total amount paid for the purchase = $204620.8
c) The total interest paid over the life of the loan = $104620.8
In this question we have been given that a man buys a house for $175,000. He makes a $75,000 down payment and amortizes the rest of the debt with semiannual payment sover the next 10 years. The interest rate on the debt is 12%, compounded semiannually.
We need to find the size of each payment, the total amount paid for the purchase and the total interest paid over the life of the loan.
From given data we get 175,000 - 75,000 = $100,000 amount to finance.
We know that the formula for semiannual payment of a loan,
C = PV/[1 - (1 + r)^-t / r]
Here, PV = $100,000
t = 20 (10 years times 2 payment per year)
r = 0.06 (12% annual. so, we divide by 2 to get semiannual)
So, C = 100,000/[1 - (1 + 0.06)^-20 / 0.06]
C = 100,000/[0.6882 / 0.06]
C = 100,000/11.47
C = $8718.4
The total interest paid will be the cuota times the time of the loan:
Total interest paid:
8718.4 x 12 = 104620.8
And the total amount paid over the life of the loan = 104620.8 + 100,000
= $204620.8
The interest will be the difference between the total amount paid and the principal of the loan
Therefore, Interest paid = $8718.4
total payment = $204620.8
principal = $100,000
Interest expense = $104620.8
Learn more about the interest here:
https://brainly.com/question/13739112
#SPJ4
What are the midline, amplitude, and period of the graphed sine function?
The midline of the function is at y= ________.
The amplitude of the function is __________.
The period of the function is _________ pi.

Answers
The midline, amplitude and period respectively of the given sine graph are; x = 1; 2; π
Midline, Amplitude and Period
The midline of this trigonometric graph is defined as the horizontal line that divides the maximum and minimum point distance into two equal parts. In this case, the midline is x = 1
The amplitude of a graphed function is usually the peak of the wave of that graph. In this case, we see that the peak of the graph is at y = 4. Thus, Amplitude = 4
Period is the difference between two consecutive maximum or minimum points. In this graph, the period is π
Read more about Midline, Amplitude and Period at; https://brainly.com/question/21124447
Answer:
Midline: y = 1
Amplitude = 3
Period = 1\(\pi\)
Step-by-step explanation:
Edmentum
The Chambers family has driven 603 miles at a constant speed of 67mph. How many hours have they been driving. Use d = rt to solve.
Write an equation for the situation that will represent the distance for any time.
Answers
Answer:
d = 67t
and
eqn d = 67t represents d over time.
Step-by-step explanation:
part one : find the hours they have been driving
d = 603 miles driven
r = 67 mph
t = ?
r = d/t
rt = d
t = d/r
t = 603/67
t = 9
unit = in hours
they have been driving for 9 hours.
part 2 : find an equation for the situation that represents distance for any time
t is the independent variable
d will represent the dependent variable
let r represent the slope
d = rt
d = 67t
therefore the eqn d = 67t represents d over time.
A bowl contains 6 apples, 3 oranges and 5 pears. If five pieces of fruit are drawn without replacement, what is the probability of picking:
a) exactly 4 pears
b) at least 2 apples
c) how many apples would you expect to pick out of the 5 pieces of fruit?
Answers
Answer:
Step-by-step explanation:
4choose 2
group the like terms separately? 3v^5-10v^2-12v^5+14v^2
Answers
the standard deviation is best described as a measure of
Answers
The standard deviation is best described as a measure of the spread of a distribution around its mean or expected value.
What is standard deviation?
Standard deviation (SD) is a numerical measurement of how spread out or dispersed a set of data is. It can be expressed as the square root of variance (s²), which is the average deviation of a data point from the mean.
What is the formula for standard deviation?
The formula for standard deviation can be written as:
s = √(Σ (Xi - µ)² / (n - 1))
where:s = standard deviation
Σ = sum
Xi = each data point
µ = the mean of the data points
n = number of data points
To know more about standard deviation visit
https://brainly.com/question/475676
#SPJ11
1. Differentiate the function f(x) = ln (81 sin^2 (x)) f’(x) 2. Differentiate the function P(t) = in ( √t2 + 9) p' (t) 3. if x2 + y2 + z2 = 9, dx/dt = B, and dy/dt = 4, find dz/dt when (x,y,z) = (2,2,1)
dz/dt =
Answers
First you will get 4dz
The distance from Earth to the moon is 384,400 kilometers. What is this distance expressed in scientific notation?
A. 3. 844E5 kilometers
B. 3. 844 × 105 kilometers
C. 3. 844E-5 kilometers
D. 3. 844E-6 kilometers
E. 3. 844 × 106 kilometers
F. 3. 844E6 kilometers
G. 3. 844 × 10-6 kilometers
H. 3. 844 × 10-5 kilometers
This is multiple choice
Answers
The distance from Earth to the moon, 384,400 kilometers, can be expressed in scientific notation as \(3.844 \times 10^5\) kilometers, or as A. \(3.844 \times 10^5\) kilometers. This is a standard way to express large numbers in science and mathematics.
The distance from Earth to the moon is 384,400 kilometers. Scientific notation is a convenient way to express large or small numbers, especially in scientific and mathematical calculations. It involves writing a number in the form of \(a \times 10^n\), where "a" is a number between 1 and 10, and "n" is an integer that determines the magnitude of the number.
To express 384,400 kilometers in scientific notation, we need to move the decimal point so that we have a number between 1 and 10. We can do this by dividing the number by 10 until we get a number between 1 and 10.
To get from 384,400 to a number between 1 and 10, we need to divide by 100,000:
384,400 kilometers = \(3.844 \times 10^5\) kilometers
This is the standard form for expressing large numbers in scientific notation, where the number is expressed as the product of a decimal number between 1 and 10 and a power of 10 that indicates the number of places the decimal point has been moved.
To learn more about scientific notation
https://brainly.com/question/18073768
#SPJ4
Consider the quadric function f(x)=9x^2+30x+25=0
Answers
Answer:
im not sure my bad
Step-by-step explanation:
the answer is 0 , the solution is 1
Step-by-step explanation: