In one tailed T-test, if the test statistics ist and to is the t-value under null hypothesis, then p-value = Prít > to alternate hypothesis is true) if ty > O and p-value = Pr(t < to alternate hypothesis is true) if to < 0. O True O False U
Answers
In a one-tailed T-test, if the test statistics and the t-value are under the null hypothesis, then p-value = ρ > to alternate hypothesis is true.
Critical zones in hypothesis testing are ranges of distributions where the values correspond to outcomes that are statistically significant. Analysts set the significance level (alpha) and whether the test is one-tailed or two-tailed in order to determine the size and location of the key regions.
The likelihood of rejecting an accurate null hypothesis is the significance level.
A test statistic's sample distribution assumes that the null hypothesis is true.
As a result, you need to shade the necessary fraction of the distribution to depict the crucial areas on the distribution for a test statistic. You shade 5% of the distribution using the typical significance threshold of 0.05.
To know more about hypothesis testing visit: brainly.com/question/17099835
#SPJ4
Related Questions
In the sketch below, AABC is similar to AXYZ. Find the length of side b.

Answers
Given
triangle ABC is similar to triangle XYZ
Find
length of side b
Explanation
Since both triangles are similar. So ratio of there sides will be equal
\(\begin{gathered} \frac{AB}{XY}=\frac{AC}{XZ} \\ \\ \frac{15}{10}=\frac{b}{8} \\ \\ b=\frac{3}{2}\times8=3\times4=12 \end{gathered}\)Final Answer
Length of side b is 12
A recent survey showed that exactly 38%
of people in a town buy the local
newspaper. There are 2450 people in the
town.
a) How many people in the town buy the
local newspaper?
b) How many people in the town do not
buy the local newspaper?
Answers
Answer:
a) .38 × 2,450 = 931 people buy the local newspaper.
b) 2,450 - 931 = 1,519 people do not buy the local newspaper.
Write an equivalent algebraic equation for the sentence below.
the quotient of x and 7 is eqyal to the difference of x and 4
Answers
Answer:
7x = x - 4 (or 6x = -4 if you want to simplify)
Step-by-step explanation:
question is pictured below, need to learn steps to solve this and I dont have my book with me
Answers
However, I can still give you some general steps to solve a math problem in 200 words.
Step 1: Read the problem thoroughly and understand what it's asking you to find. This may involve identifying the given information and what you need to find. Also, identify any constraints on the problem, like time or cost.
Step 2: Plan how to solve the problem. Think about what mathematical operations or formulas you can use to find the answer. Make a list of the steps you need to take to solve the problem. Also, determine the units for your answer.
Step 3: Solve the problem. Use the mathematical operations or formulas you've identified in step 2 to find the answer. Show all of your work, including any calculations, so that you can easily check your work later.
Step 4: Check your answer. Make sure that your answer makes sense and that it satisfies any constraints given in the problem. Also, check that your units are correct. If your answer doesn't make sense, go back and review your work to see if you made an error.
Step 5: Reflect on what you've learned. Think about what you did well and what you could improve upon in future problem-solving situations. This will help you become a more effective problem solver in the future.
For such more question on constraints
https://brainly.com/question/29989358
#SPJ8
y − 6 =3/5(x + 5); (0, 8)
Answers
The equation of a line parallel to the given line and passing through the point (0, 8) is 5y - 3x = 40
Equation of a lineThe equation of a line in point-slope form is expressed as;
y - y0 = m(x -x0)
where
m is the slope
(x0, y0) is the point on the line
Given the following parameters
Point (0,8)
Slope from the equation = 3/5
Substitute
y - 8 = 3/5(x - 0)
5(y -8) =3x
5y - 40 = 3x
5y - 3x = 40
Hence the equation of a line parallel to the given line and passing through the point (0, 8) is 5y - 3x = 40
Learn more on equation of a line here: https://brainly.com/question/13763238
#SPJ1
If Jorgen has $4,000,000,000,000 And he wants to buy a truck123456789,-0000000000000000000000000000000000000,00000000000000000000000,00000000000000000000 haw much will he need to save up to buy the truck?
Answers
He doesn't need a truck. He can buy an aeroplane.
Answer:
Jorgen would still have enough money for the truck.
Step-by-step explanation:
Seeing as - (or negative) 0000000000000... isn't a real number and you put a comma after the 123456789, Jorgen would actually have enough for the truck. If you actually wanted the truck to be worth 123456789000000000... Jorgen would need to save up more than 9 octovigintillion to reach his goal of getting the truck, and that is one expensive truck.
What is the measure of the angle?

Answers
how many different types of omlettes can be prepared with 10 ingredients?
Answers
how many different types of omlettes can be prepared with 10 ingredients? 7
Answer:
1024 omelets
Step-by-step explanation:
2^10 = 1024
A manager at a shopping mall counts 244 males and n females as they enter the mall. The manager realizes that 25% of all males and 25% of all females are children. She writes the expression 0.25n + 61 to represent the number of children who enter the mall. Is the manager correct? Why or why not?
The manager (blank, choose is or is not) correct because the original expression 0.25(n + 244) (blank, choose is or is not) equivalent to the manager’s expression, 0.25n + 61.
Answers
Answer:
The manager is not correct in her calculation.
Step-by-step explanation:
There are 244 males and n females who entered the mall as the manager at the shopping mall counts.
If 25% of all males are children, then the number of male children are .
Again, the 25% of all female are children, then the number of female chilfren are .
Therefore, the total number of children will be (60 + 0.25n).
But the manager gives the number of children to be 0.25n + 61 who entered the mall.
So, the manager is not correct in that calculation. (Answer)
Step-by-step explanation:
Based on an indication that mean daily car rental rates may be higher for Boston than for Dallas, a survey of eight car rental companies in Boston is taken and the sample mean car rental rate is $47, with a standard deviation of $3. Further, suppose a survey of nine car rental companies in Dallas results in a sample mean of $44 and a standard deviation of $3. Use alpha = 0.05 to test to determine whether the average daily car rental rates in Boston are significantly higher than those in Dallas. Assume car rental rates are normally distributed and the population variances are equal. The null hypothesis for this problem is ______.
a) μ1 - μ2 < 0
b) μ1 - μ2 > 0
c) μ1 - μ2 = 1
d) μ1 - μ2 ≠ 0
e) μ1 - μ2 = 0
Answers
Answer:
Step-by-step explanation:
This is a test of 2 independent groups. The population standard deviations are not known. Let μ1 be the mean daily car rental rates for Boston and μ2 be the mean daily car rental rates for Dallas.
The random variable is μ1 - μ2 = difference in the mean daily car rental rates for Boston and the mean daily car rental rates for Dallas
We would set up the hypothesis.
The null hypothesis is
H0 : μ1 = μ2 H0 : μ1 - μ2 = 0
The alternative hypothesis is
H1 : μ1 > μ2 H1 : μ1 - μ2 > 0
Since sample standard deviation is known, we would determine the test statistic by using the t test. The formula is
(x1 - x2)/√(s1²/n1 + s2²/n2)
From the information given,
μ1 = 47
μ2 = 44
s1 = 3
s2 = 3
n1 = 8
n2 = 9
t = (47 - 44)/√(3²/8 + 3²/9)
t = 1.41
The formula for determining the degree of freedom is
df = [s1²/n1 + s2²/n2]²/(1/n1 - 1)(s1²/n1)² + (1/n2 - 1)(s2²/n2)²
df = [3²/8 + 3²/9]²/[(1/8 - 1)(3²/8)² + (1/9 - 1)(3²/9)²] = 4.515625/0.28571428571
df = 16
We would determine the probability value from the t test calculator. It becomes
p value = 0.09
Since alpha, 0.05 < than the p value, 0.09, then we would fail to reject the null hypothesis.
What is the axis of symmetry for the quadratic equation from Question 1: f(x) = 0.5(x+3)(x-7)?
Answers
We know that for an equation of the form:
\(f(x)=ax^2+bx+c\)the axis of symmetry is given by:
\(x=-\frac{b}{2a}\)In this case, where our formula is given by the equation:
\(f\mleft(x\mright)=0.5\mleft(x+3\mright)\mleft(x-7\mright)\)we want to multiply all the factors so we can work with the form of the first equation. We do this using the distributive property:
0.5 (x + 3) = 0.5 · x + 0.5 · 3
= 0.5x + 1.5
Then, in the equation:
\(\begin{gathered} f(x)=0.5(x+3)(x-7) \\ \downarrow \\ f(x)=(0.5x+1.5)(x-7) \end{gathered}\)Now, multiplying both (0.5x + 1.5) and (x - 7) we have that:
\(\begin{gathered} f(x)=(0.5x+1.5)(x-7) \\ \downarrow \\ f(x)=(0.5x+1.5)\cdot x-(0.5x+1.5)\cdot7 \end{gathered}\)Now, finding the product of
(0.5x + 1.5)x, we have that:
\(\begin{gathered} \mleft(0.5x+1.5\mright)x \\ =0.5x\cdot x+1.5\cdot x \\ =0.5x^2+1.5x \end{gathered}\)Replacing in the equation:
\(\begin{gathered} f(x)=(0.5x+1.5)\cdot x-(0.5x+1.5)\cdot7 \\ \downarrow \\ f(x)=0.5x^2+1.5x-(0.5x+1.5)\cdot7 \end{gathered}\)On the other hand, finding the product of
-(0.5x + 1.5) · 7,we have that
-(0.5x + 1.5) · 7 = -0.5x · 7 - 1.5 · 7
= -3.5x - 10.5
Replacing in the equation:
\(\begin{gathered} f(x)=0.5x^2+1.5x-(0.5x+1.5)\cdot7 \\ \downarrow \\ f(x)=0.5x^2+1.5x-3.5x-10.5 \\ f(x)=0.5x^2-2x-10.5 \end{gathered}\)Then, we have that
a = 0.5,
b = -2
and
c = -10.5
Then, using the equation for the axis of symmetry, we have that:
\(\begin{gathered} x=-\frac{b}{2a} \\ \downarrow \\ x=-\frac{(-2)}{2\cdot0.5} \\ x=\frac{2}{2\cdot0.5}=\frac{1}{0.5} \\ \downarrow \\ x=2 \end{gathered}\)
El perro de Antonia debe comer 0,48 kg de alimento cada día. ¿Cuánto alimento necesita para 30 días?
Answers
Answer:
Amount of food need for 30 days = 14.4 kilogram
Step-by-step explanation:
Given information:
Amount of food dog eat each day = 0.48 kilogram
Find:
Amount of food need for 30 days
Computation:
⇔ Amount of food need for 30 days = Amount of food dog eat each day x number of days
⇔ Amount of food need for 30 days = 0.48 x 30
Amount of food need for 30 days = 14.4 kilogram
14.4 kilogram is right answer.
The area of a rectangle is 3,878 square centimeters. If the rectangle has a width of 14 centimeters, what is its length?
Answers
Answer:
277 cm
Step-by-step explanation:
\(A=l*w\\3,878=l*14\\l=\frac{3,878}{14} \\l=277\)
A scientist has acid solutions with concentrations of 4% and 15%. He wants to mix some of each solution to get 44 milliliters of solution with a 12% concentration. How many milliliters of each solution does he need to mix together?
Answers
Let x and y be the amounts (in mL) of the 4% and 15% solutions, respectively, that the scientist needs to use.
He wants to end up with a 44 mL solution, so
x + y = 44 mL
Each milliliter of 4% solution contains 0.04 mL of acid, while each mL of 15% contains 0.15 mL of acid. The resulting solution should have a concentration of 12%, so that each mL of it contains 0.12 mL of acid. Then the solution will contain
0.04x + 0.15y = 0.12 × (44 mL) = 5.28 mL
of acid.
Solve for x and y. In the first equation, we have y = 44 mL - x, and substituting into the second equation gives
0.04x + 0.15 (44 mL - x) = 5.28 mL
0.04x + 6.6 mL - 0.15x = 5.28 mL
1.32 mL = 0.19x
x ≈ 6.95 mL
==> y ≈ 37.05 mL
Identify the next number in the following sequence
25 49 97 ?
Select only one answer
- 124
- 171
- 139
- 193
Answers
Answer:
the correct answer is 193
Step-by-step explanation:
25×1-0=25
25×2-1=49
49×2-1=97
97×2-1=193
Verify that parallelogram ABCD with vertices A(-5, -1), B(-9, 6), C(-1, 5), and D(3, is a rhombus by showing that it is a parallelogram with perpendicular diagonals.

Answers
multiplication of the gradients of the two diagonals is equals to -1 if they are perpendicular

Can you please help me
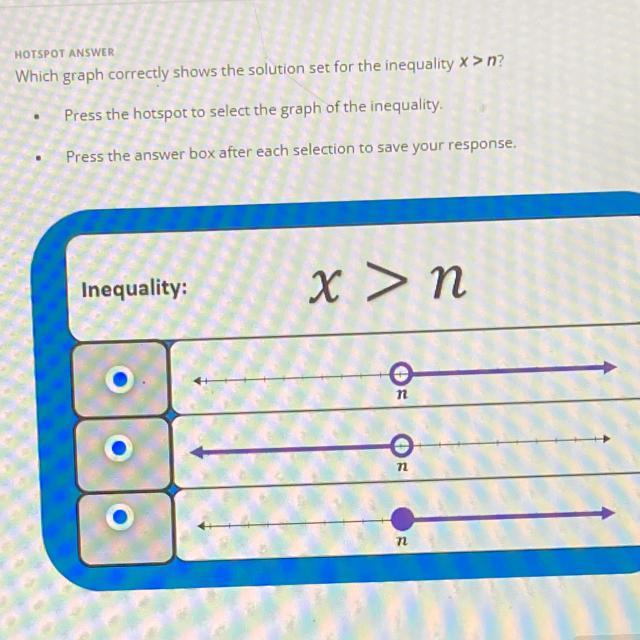
Answers
Answer:
first graph
Step-by-step explanation:
x > n
the graph will have an open circle at the value n , indicating that x cannot equal n ( note solid circle if x ≥ n )
the arrow from n will point in the right direction, indicating values of x greater than n.
the graph representing x > n is the first graph
at noon, ship a is 150 km west of ship b. ship a is sailing east at 30 km/h and ship b is sailing north at 20 km/h. how fast (in km/hr) is the distance between the ships changing at 4:00 p.m.? (round your answer to three decimal places.)
Answers
At 4:00 pm, the distance between the ships changing at 9.81 km/h
In this question we hve been given that at noon, ship A is 150 km west of ship B.
Ship A is sailing east at 30 km / h and ship B is sailing north at 20 km / h, We need to determine how fast is the distance between the ships changing at 4:00 PM.
The displacement of ship A at 4pm is
= 150 km - (30 km/h * 4h)
Since A is moving away from the initial position and the distance between the two ships is decreasing.
= 140 km - 120 km
= 20 km
The displacement of ship B at 4pm would be,
20 km/h * 4h = 80 km
Using Pythagoras theorem, the resultant displacement of the two ships at 4pm would be,
r² = a² + b²
r² = 20² + 80²
r = √6800
r = 82.46 km
The rate of change of this distance is calculated as;
r² = a² + b²
2r(dr/dt) = 2a(da/dt) + 2b(db/dt)
r(dr/dt) = a(da/dt) + b(db/dt)
r = 101.98 km, a = 20 km, b = 80 km
101.98(dr/dt) = 20(-30) + 80(20)
101.98(dr/dt) = 1000
(dr/dt) = 1000/101.98
dr/dt = 9.81 km/h
Therefore, the distance between the ships changing at 9.81 km/h
Learn more about Pythagoras theorem here:
https://brainly.com/question/343682
#SPJ4
2. Write the absolute value of the following. a) | -6 -3 | . b) | 0 - 12 |.
Answers
Answer:
a)9. b) 12
Step-by-step explanation:
a) | -6 -3 | .
-6-3 = -9
|-9| =9
b) | 0 - 12 |.
0-12=-12
|-12|=12
A friend has a 84% average before the final exam for a course. That score includes everything but the final, which counts for 25% of the course grade.
What is the best course grade your friend can earn?
%
What is the minimum score would your friend would need on the final to earn a 75% for the course?
%
Give answers accurate to at least one decimal place.
Answers
75% of his grade is an 84%
25% of his grade is a 100% (final)
.75(.84) + .25(1) = .88 or 88%
Minimum score
.75 = .75(.84) + .25x
.75 = .63 + .25x
.12 = .25x
x = .48 or 48%
1 point
If one person can stand on a 4 square feet floor area, how many persons
can stand on 64 square foot floor area? Which proportion accurately solves
this problem? *
A) 1/4= X/64
B) 1/4= 64/x
C)1/64= 4/x
D)4/64= x/1
Answers
Answer:
A) 1/4=X/64
Step-by-step explanation:
It's 1 person every 4 square feet on the floor area so 1/4 would represent that and since we don't know the number of people that fit on 64 square feet on the floor area it would be x/64.
Hope that helps!
I don’t know this one question

Answers
Answer:
v = 13
Step-by-step explanation:
because they are supplementary angles they add up to 180
so
add them
and put them equal to 180
9v + 3 + 60 = 180
combine like terms
9v + 63 = 180
now subtract 63 to both sides
9v = 117
divide 9 to both sides
v = 13
that is your answer
The next model of a sports car will cost 14.7% more than the current model. The current model costs $34,000. How much will the price increase in dollars?
What will be the price of the next model?
Increase in price:
Price of next model:
Answers
Answer: $4,998
Step-by-step explanation:
34000*1.147
38998-34000=4998
The conjugate of 145+ 145/3
Answers
Answer:
193 1/3
Step-by-step explanation:
First, we need to convert \(\frac{145}{3}\) into a mixed number.
\(\frac{145}{3}\) = \(48\) \(\frac{1}{3}\)Now, we can add them together:
\(145 +48\frac{1}{3} = 193 \frac{1}{3}\)Therefore, the answer is \(193\frac{1}{3}\).
The graph to the right is the uniform probability density function for a friend who is x minutes late. (a) Find the probability that the friend is between 10 and 30 minutes late. (b) It is 10 A.M. There is a 20% probability the friend will arrive within how many minutes? part a) what is the probability that the friend is between 10 and 30 minutes late_?

Answers
The probability that the friend is between 10 and 30 minutes late is approximately 0.6667, or 66.67%.
Since the probability density function is uniform, the probability of the friend being between 10 and 30 minutes late is equal to the area of the rectangle that lies between x = 10 and x = 30, and below the curve of the probability density function.
The height of the rectangle is equal to the maximum value of the probability density function, which is 1/30 since the interval of possible values for x is [0, 30] minutes.
The width of the rectangle is equal to the difference between the upper and lower limits of the interval, which is 30 - 10 = 20 minutes.
Therefore, the probability of the friend being between 10 and 30 minutes late is:
P(10 < x < 30) = (height of rectangle) x (width of rectangle)
= (1/30) x 20
= 2/3
≈ 0.6667
So the probability that the friend is between 10 and 30 minutes late is approximately 0.6667, or 66.67%.
To know more about probability follow
https://brainly.com/question/27077702
#SPJ1
the radius of a cylindrical water tank is 4ft, and it’s height is 10ft. What is the volume of the tank?

Answers
Answer:
\(volume = 502.4ft^3\)
Step-by-step explanation:
\(volume = \pi r^2 h = 3.14 \times 4^2 \times 10 = 502.4ft^3\)
5. Halle la solucion de las siguientesecuaciones.
2x + 6 = 10 + x
Answers
\(\tt{Hey~there!\)
\(\tt{2x+6=10+x\)
\(\tt{Simplify~both~sides~of~the~equation:\)
\(\tt{2x+6=x+10\)
\(\tt{Subtract~x~from~both~sides:\)
\(\tt{2x+6-=x+10-x\)
\(\tt{x+6=10\)
\(\tt{Subtract~6~from~both~sides:\)
\(\tt{x+6-6=10-6\)
\(\boxed{\tt{x=4}}\)
\(\tt{Hope~this~helps!\)
\(\boxed{\tt{-TestedHyperr}}\)
can you show step by step how to work the following 3/4-7/9+2/3
Answers
Answer:
hopefully this helps:)

Answer:
23/36 (can't be simpified)
Step-by-step explanation:
3/4 - 7/9 + 2/3
All of the denominators have to be the same in order to do these operations.
How do we get the denomiators to be the same?
We find the least commom multiple (LCM) of of 4, 9, and 3.
The LCM is 36.
Now, let's stop here for a moment. How did we get the LCM? We have to find a number that all the denominators go into evenly. But how do we do that?
We can multiply four and three, and we get twelve. But what about nine? Does nine go into twelve evenly? No; therefore twelve isn't the LCM. Now let's try multiplying nine and three. Nine times three is twenty-seven, but four can't evenly go into twenty-seven. Because of this, twenty-seven isn't the LCM. Lastly, let's try multiplying four and nine. Four times nine is thirty-six, but does three go into thirty-six? Because three times twelve is thirty-six, we have found our LCM.
You can do it this way, but there is an easier way to solve the problem.
All you have to do is multiply the denominators (in this case, it would be four, nine, and three) and you have your common multiple. But be aware! If you do this all the time, you won't always find the least common multiple. After you have solved the problem, the answer may need to be simplified. But, after you simplify, the answer will be the same as if you did it the other way.
Now, we have it where the denominators of ALL the fractions are 36. But we are still not done here.
?/36 - ?/36 + ?/36
Lets look at the first fraction. The original denominator was 4.
In order to get the numerator, ask yourslef this:
How did we go from four to thirty-six?
You then think:
Four times what is thirty-six?
or
Thirty-six divided by four is what?
The answer: nine
Four times nine is thirty-six
Thirty-six divided by four is nine
Our next step:
Because we multiplied four by nine, we are going to multiply the numerator (three) by nine
Therefore, we have 3 times 9 in the numerator, which becomes 27.
27/36 - ?/36 + ?/36
We now look at the second fraction. The original denominator was 9.
How did we go from nine to thirty-six?
Nine times what is thiry-six?
Nine times four is thirty-six.
We multiplied nine and four, so we're going to multiply the numerator (seven) by four
Therefore, we have 7 times 4 in the numerator, which becomes 28.
27/36 - 28/36 + ?/36
Lastly, we look at the last fraction. The original denominator was 3.
How did we go from three to thirty-six?
Three times what is thirty-six?
Three times twelve is thirty-six.
We multiplied three and twelve, so we're going to multiply the numerator (two) by twelve
Therefore, we have 2 times 12 in the numerator, which becomes 24.
Yassss! We now have our problem that we can finally solve!
27/36 - 28/36 + 24/36
-1/36 + 24/36
23/36
We get -1/36 by subtracting 27/36 and 28/36. When we do this, the denominator stays the same. So really, we're subtracting 27 and 28, which is -1.
We then need to add -1/36 and 24/36, but once again, the denominators stay the same. So really, we're adding -1 and 24, which is 23.
Hope this helps! Let me know if you have any questions! :)
Math 132 final exam grade is normally distributed with mean 68 and standard deviation 23. Final exam score above 92 corresponds to an A Approximately what percent of the class gotan A?
Answers
Since the function is a normal distribution, we can use the z-score formula shown below
\(Z=\frac{x-\mu}{\sigma}\)In our case,
\(\mu=68,\sigma=23\)Then, set x=92 and solve for Z
\(\begin{gathered} x=92 \\ \Rightarrow Z=\frac{92-68}{23}=\frac{24}{23} \\ \Rightarrow Z=\frac{24}{23}=1.04347\ldots \end{gathered}\)Using a z-score table, the cumulative probability of Z=24/23 is
\(\Rightarrow P(X\le92)=0.8508\)Finally,
\(\begin{gathered} \Rightarrow P(X>92)=1-P(X\le92)=1-0.8508=0.1492 \\ \Rightarrow P(X>92)=0.1492 \end{gathered}\)Thus, the answer is 0.1492, which is equivalent to 14.92%; rounded to the nearest percentage, the answer is 15%
What is the product of 2x -5 and 3x^2 + 5x - 7? Write your answer in standard form. A. Show your work. B. Is the product of 2x -5 and 3x^2 + 5x -7 equal to the product of 5x - 2 and 3x^2 + 5x - 7? Explain your answer.
Answers
Answer:
A)What is the product of 2x -5 and 3x^2 + 5x - 7? Write your answer in standard form.
6x³ - 5x² - 39x + 35 = 0
B. Is the product of 2x -5 and 3x^2 + 5x -7 equal to the product of 5x - 2 and 3x^2 + 5x - 7?
No it is not.
Step-by-step explanation:
A)What is the product of 2x -5 and 3x^2 + 5x - 7? Write your answer in standard form.
(2x - 5) (3x² + 5x - 7)
= 2x(3x² + 5x - 7) -5(3x² + 5x - 7)
= 6x³ + 10x² - 14x -15x² - 25x +35
Collecting like terms
= 6x³ +10x² - 15x² - 14x - 25x +35
= 6x³ - 5x² - 39x + 35
In standard form
6x³ - 5x² - 39x + 35 = 0
B. Is the product of 2x -5 and 3x^2 + 5x -7 equal to the product of 5x - 2 and 3x^2 + 5x - 7?
First we find the product of
5x - 2 and 3x² + 5x - 7?
(5x - 2) (3x² + 5x - 7)
5x(3x² + 5x - 7) -2(3x² + 5x - 7)
15x³ + 25x² - 35x - 6x² -10x + 14
Collect like terms
15x³+ 25x² - 6x² -35x - 10x + 14
15x³ + 19x² - 45x + 14 = 0
Hence, the product of 5x - 2 and 3x^2 + 5x - 7
= 15x³ + 19x² - 45x + 14 = 0
The product of 2x -5 and 3x^2 + 5x -7 = 6x³ - 5x² - 39x + 35 = 0
Comparing both products, we can see that
The product of 2x -5 and 3x^2 + 5x -7 ≠ the product of 5x - 2 and 3x^2 + 5x - 7