In a class of students, the following data table summarizes how many students passed a test and complete the homework due the day of the test. What is the probability that a student chosen randomly from the class passed the test? Passed the test Failed the test Completed the homework 16 3 Did not complete the homework 4 6
Answers
To find the probability that a student chosen randomly from the class passed the test, we need to find the total number of students who passed the test and divide it by the total number of students in the class.
The total number of students who passed the test is the sum of the number of students who passed and completed the homework and the number of students who passed but did not complete the homework, which is 16 + 3 = 19.
The total number of students in the class is the sum of all four values in the table, which is 16 + 3 + 4 + 6 = 29.
Therefore, the probability that a student chosen randomly from the class passed the test is 19/29, which is approximately 0.655 or 65.5%.
Related Questions
A party rental company has chairs and tables for rent. The total cost to rent 4 chairs and 8 tables is 89 . The total cost to rent 2 chairs and 3 tables is 34 . What is the cost to rent each chair and each table?
Answers
Answer:
Let C = cost to rent each chairLet T = cost to rent each table 4C + 8T = 732C + 3T = 28 Multiply the 2nd equation by (-2) and then add the equations together 4C + 8T = 73-4C - 6T = -56 2T = 17T = 17/2 = 8.5 Plug this in to the 1st equation to solve for C 4C + 8(17/2) = 734C + 68 = 734C = 5C = 5/4 = 1.25 So the cost to rent each chair is $1.25 and the cost to rent each table is $8.50
Step-by-step explanation:
Real-life Problems Question 6

Answers
The amount of money that Theresa has left is equal to £2,740.
How to write a linear equation to model this situation?In order to write a linear equation to describe this situation, we would assign variables to the cost of flights for each of them and the cost of accommodation for each of them respectively, and then translate the word problem into a linear equation as follows:
Let the variable a represent cost of flights for each of them.
Let the variable f represent cost of accommodation for each of them.
Since Theresa paid for herself and 11 friends to go on holiday with a flight cost of £339 and accommodation cost of £266, a linear equation to describe this situation is given by;
y = 12(a + b)
y = 12(266 + 339)
y = £7,260
For the amount of money left, we have:
Amount of money left = £10,000 - £7,260
Amount of money left = £2,740.
Read more on equation here: brainly.com/question/18912929
#SPJ1
HELP ME PLEASE SOMEONE

Answers
Answer:
x = 3
Step-by-step explanation:
15x + 8 and 9x + 26 are corresponding angles and are congruent , then
15x + 8 = 9x + 26 ( subtract 9x from both sides )
6x + 8 = 26 ( subtract 8 from both sides )
6x = 18 ( divide both sides by 6 )
x = 3
Thembi leaves school at 07:10 to get to school at 07:45. How long does it take her to school and home each week?
Answers
The number of hours, t, that bacteria spread 10-fold can be modeled by the equation B(t) = B0(10)4t. There are 50 bacteria present initially and a biologist wishes to find out how many hours will elapse until there are 10,000 bacteria present. What is the exact value for the number of hours elapsed, t, in the equation 10,000 = 50(10)4t?
Answers
Answer:
t = (log200)/4 hours
Step-by-step explanation:
10,000 = 50(10)^(4t)
Divide both sides by 50
200 = 10^(4t)
Take the log of both sides
log200 = 4t
Divide both sides by 4
(log200)/4 = t
t = (log200)/4 (exact answer)
t ≈ 0.575257498915995 (numeric approximation)
I’m stuck, help would be nice :D

Answers
Answer:
-14
Explanation:
3 x -3 - 5 = -14
Answer:
-14, -5, 4, and 13
Step-by-step explanation:
For each x value, substitute it for x in the equation.
For the first one where x = -3,
y = 3(-3) - 5
y = -9 - 5
y = -14
So the first one is -14. The next x value is 0
y = 3(0) - 5
y = 0 - 5
y = -5
Second one is -5. The next x value is 3
y = 3(3) - 5
y = 9 - 5
y = 4
Third is 4. The next x value is 6
y = 3(6) - 5
y = 18 - 5
y = 13
So the last one is 13.
NO LINKS!! URGENT HELP PLEASE!!
1. Find the area of a regular octagon. Each side is 12 m.
2. The perimeter of a regular polygon is 72 feet. An exterior angle of the polygon measures 40°. Find the length of each side.
3. If the perimeter of a regular pentagon is 50 in. Find the area. Show a drawing and work please.
Answers
Answer:
1) 695.3 m²
2) 8 ft
3) 172.0 in²
Step-by-step explanation:
Question 1To find the area of a regular polygon, we can use the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
Given the polygon is an octagon, n = 8.
Given each side measures 12 m, s = 12.
Substitute the values of n and s into the formula for area and solve for A:
\(\implies A=\dfrac{(12)^2 \cdot 8}{4 \tan\left(\dfrac{180^{\circ}}{8}\right)}\)
\(\implies A=\dfrac{144 \cdot 8}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{1152}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{288}{\tan\left(22.5^{\circ}\right)}\)
\(\implies A=695.29350...\)
Therefore, the area of a regular octagon with side length 12 m is 695.3 m² rounded to the nearest tenth.
\(\hrulefill\)
Question 2The sum of an interior angle of a regular polygon and its corresponding exterior angle is always 180°.
If the exterior angle of a polygon measures 40°, then its interior angle measures 140°.
To determine the number of sides of the regular polygon given its interior angle, we can use this formula, where n is the number of sides:
\(\boxed{\textsf{Interior angle of a regular polygon} = \dfrac{180^{\circ}(n-2)}{n}}\)
Therefore:
\(\implies 140^{\circ}=\dfrac{180^{\circ}(n-2)}{n}\)
\(\implies 140^{\circ}n=180^{\circ}n - 360^{\circ}\)
\(\implies 40^{\circ}n=360^{\circ}\)
\(\implies n=\dfrac{360^{\circ}}{40^{\circ}}\)
\(\implies n=9\)
Therefore, the regular polygon has 9 sides.
To determine the length of each side, divide the given perimeter by the number of sides:
\(\implies \sf Side\;length=\dfrac{Perimeter}{\textsf{$n$}}\)
\(\implies \sf Side \;length=\dfrac{72}{9}\)
\(\implies \sf Side \;length=8\;ft\)
Therefore, the length of each side of the regular polygon is 8 ft.
\(\hrulefill\)
Question 3The area of a regular polygon can be calculated using the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
A regular pentagon has 5 sides, so n = 5.
If its perimeter is 50 inches, then the length of one side is 10 inches, so s = 10.
Substitute the values of s and n into the formula and solve for A:
\(\implies A=\dfrac{(10)^2 \cdot 5}{4 \tan\left(\dfrac{180^{\circ}}{5}\right)}\)
\(\implies A=\dfrac{100 \cdot 5}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{500}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{125}{\tan\left(36^{\circ}\right)}\)
\(\implies A=172.047740...\)
Therefore, the area of a regular pentagon with perimeter 50 inches is 172.0 in² rounded to the nearest tenth.
Answer:
1.695.29 m^2
2.8 feet
3. 172.0477 in^2
Step-by-step explanation:
1. The area of a regular octagon can be found using the formula:
\(\boxed{\bold{Area = 2a^2(1 + \sqrt{2})}}\)
where a is the length of one side of the octagon.
In this case, a = 12 m, so the area is:
\(\bold{Area = 2(12 m)^2(1 + \sqrt{2}) = 288m^2(1 + \sqrt2)=695.29 m^2}\)
Therefore, the Area of a regular octagon is 695.29 m^2
2.
The formula for the exterior angle of a regular polygon is:
\(\boxed{\bold{Exterior \:angle = \frac{360^o}{n}}}\)
where n is the number of sides in the polygon.
In this case, the exterior angle is 40°, so we can set up the following equation:
\(\bold{40^o=\frac{ 360^0 }{n}}\)
\(n=\frac{360}{40}=9\)
Therefore, the polygon has n=9 sides.
Perimeter=72ft.
We have
\(\boxed{\bold{Perimeter = n*s}}\)
where n is the number of sides in the polygon and s is the length of one side.
Substituting Value.
72 feet = 9*s
\(\bold{s =\frac{ 72 \:feet }{ 9}}\)
s = 8 feet
Therefore, the length of each side of the polygon is 8 feet.
3.
Solution:
A regular pentagon has five sides of equal length. If the perimeter of the pentagon is 50 in, then each side has a length = \(\bold{\frac{perimeter}{n}=\frac{50}{5 }= 10 in.}\)
The area of a regular pentagon can be found using the following formula:
\(\boxed{\bold{Area = \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *s^2}}\)
where s is the length of one side of the Pentagon.
In this case, s = 10 in, so the area is:
\(\bold{Area= \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *10^2=172.0477 in^2}\)
Drawing: Attachment

PLEASE HELP ME
The function f(x) = -2(4)^x+1 +140
represents the number of tokens a child has x hours after arriving at an arcade.
What is the practical domain and range of the function?
If necessary, round to the nearest hundredth.
The practical domain of the situation is ?
The practical range of the situation is ?
PLEASE SEE PHOTO FOR FUNCTION

Answers
The function f(x) = -2(4)ˣ⁺¹ +140 represents the number of tokens a child has x hours after arriving at an arcade. The practical domain and range of the function are x ≥ 0 and The practical range of the situation is [140, ∞).
The given function is f(x) = -2(4)ˣ⁺¹+ 140, which represents the number of tokens a child has x hours after arriving at an arcade.
To determine the practical domain and range of the function, we need to consider the constraints and limitations of the situation.
For the practical domain, we need to identify the valid values for x, which in this case represents the number of hours the child has been at the arcade. Since time cannot be negative in this context, the practical domain is x ≥ 0, meaning x is a non-negative number or zero.
Therefore, the practical domain of the situation is x ≥ 0.
For the practical range, we need to determine the possible values for the number of tokens the child can have. Looking at the given function, we can see that the term -2(4)ˣ⁺¹represents a decreasing exponential function as x increases. The constant term +140 is added to shift the graph upward.
Since the exponential term decreases as x increases, the function will have a maximum value at x = 0 and approach negative infinity as x approaches infinity. However, due to the presence of the +140 term, the actual range will be shifted upward by 140 units.
Therefore, the practical range of the situation will be all real numbers greater than or equal to 140. In interval notation, we can express it as [140, ∞).
To summarize:
- The practical domain of the situation is x ≥ 0.
- The practical range of the situation is [140, ∞).
Know more about the domain here:
https://brainly.com/question/30096754
#SPJ8
Find the exact solutions of the given equation in the interval .
sin 4x= –2sin 2x

Answers
The exact solutions of the given equation in the interval are;
A: x = 0, π/2, π, ³/₂π
How to find the exact solutions of trigonometric equations?
We are given the equation as;
sin 4x = –2sin 2x
Writing the equation in standard form gives;
sin 4x + 2sin 2x = 0
Using trigonometric Identity, substitute (sin 4x) with (2sin 2x.cos 2x) to get;
2sin 2x cos 2x + 2sin 2x = 0
Factorize to get;
2sin 2x(cos 2x + 1) = 0
A. sin 2x = 0
The unit circle will give us 3 solutions for 2x as follows;
2x = 0
Thus; x = 0
2x = π
Thus; x = π/2
2x = 2π
Thus; x = π
B. cos 2x = - 1
The unit circle gives 2 solutions for 2x as;
2x = π
Thus; x = π/2
2x = 3π
Thus; x = ³/₂π
Read more about solutions of trigonometric equations at; https://brainly.com/question/28921050?source=archive
#SPJ1
Complete question is;
How do you find the exact solutions of the equation sin4x = −2sin2x in the interval [0, 2π)?
help neededdd.......

Answers
Answer:
1. -5a
Step-by-step explanation:
The definition of combining like terms is adding their coefficients, for example: 2x + 3x = (2+3)x = 5x.
So for this one, -21a+16a = (-21+16)a = -5a.
How many 4-digit passcodes can be created if each digit can be any number, 0-9?
6,561
10,000
40
5,040
Answers
Answer:
6,561
that's a good number
0 thru 9 is 10 numbers.
Each digit can be 1 of 10 numbers:
Total combinations = 10 x 10 x 10 x 10 = 10,000
Answer: 10,000
-22 + (-10) + 15 I don’t know how to solve this problem
Answers
The answer is - 17
here, we have to apply BODMAS rule
given ,- 22 + (10) = 15
= - 22 - 10 + 15
= -32 + 15
= - 17
BODMAS is an acronym for the sequence of operations to be performed while simplifying the mathematical expressions.
B=Brackets
O=Off
D=Division
M=Multiplication
A=Addition
S=Subtraction
Achilles is a mathematician who invented BODMAS. It is a mnemonic that helps us remember how to evaluate mathematical operators in a mathematical statement involving more than one mathematical operation.The four basic Mathematical rules are addition, subtraction, multiplication, and division.
Basic math skills are those that involve making calculations of amounts, sizes or other measurements. Core concepts like addition, subtraction, multiplication and division provide a foundation for learning and using more advanced math concepts.
to know more about BODMAS;
visit; brainly.com/question/28627820
#SPJ9
if the earthquake has stronger magnitude what does it mean
Answers
Answer:
Step-by-step explanation:
The magnitude of an earthquake is a measure of the amount of energy released during the earthquake. A stronger magnitude generally means a more powerful earthquake.
Kelly rolled scores of 254, 202, 284, 269, 151, 258 and 202 in a recent tournament. What was the mean, median and mode of her scores?
Answers
Answer:
See below!
Step-by-step explanation:
Data:254, 202, 284, 269, 151, 258, 202
Mean:The sum of data divided by the number of data is called mean.Mean of the data:
\(\displaystyle Mean= \frac{Sum \ of \ data}{number \ of \ data} \\\\Mean = \frac{254+202+284+269+151+258+202}{7} \\\\Mean=\frac{1620}{7} \\\\\boxed{Mean = 231.4}\)
Median:The middle value of the data is median.Median of data:
Arrange the data in increasing order.
151, 202, 202, 254, 258, 269, 284
The middle value = 254
So,
Median = 254Mode:The frequently occurring value in the data is known as mode.Mode in data:
The mode, here, is 202. (occurring 2 times.)
So,
Mode = 2\(\rule[225]{225}{2}\)
Select the correct answer.
Which statement correctly compares the graph of function g with the graph of function ??
FE) = e²-
g(x) = ² - 4
O A.
OB.
O C.
O D.
The graph of function g is a horizontal shift of the graph of function to the right.
The graph of function g is a vertical stretch of the graph of function f.
The graph of function g is a vertical compression of the graph of function f.
The graph of function g is a horizontal shift of the graph of function f to the left.
Reset
Next

Answers
A statement that correctly compares the graph of function g with the graph of function f include the following: C. The graph of function g is a vertical compression of the graph of function f.
What is a dilation?In Mathematics and Geometry, a dilation is a type of transformation which typically transforms the dimension (size) or side lengths of a geometric object, without affecting its shape.
Therefore, the dimension or side lengths of the dilated geometric object would be stretched or compressed (shrunk) depending on the scale factor that is applied.
When the parent function \(f(x) = e^x -4\) is vertically compressed by a scale factor of 1/2, the transformed function g(x) is given by the following equation;
g(x) = kf(x)
g(x) = 1/2f(x)
\(g(x) = \frac{1}{2} e^x -4\)
Read more on dilation and scale factor here: brainly.com/question/4421026
#SPJ1
The radius of a circle is 3 feet. What is the length of a 75° arc?
Answers
Therefore , the solution of the given problem of circle comes out to be arc length 3.93 feet.
How do circles work?Every area of the plane that is separated by a specific amount from this additional point makes a circle (center). As a result, it is a curve made up of spots that are separated from one another on the surface. Additionally, it rotates similarly about the centre at every angle. Every collection of endpoints in the confined, two-dimensional sphere of a circle is uniformly spaced apart from the "centre."
Here,
A circle with a radius of 3 feet is equal to its diameter as follows:
=> C = 2πr = 2π(3) = 6π feet
Since there are 360° of angles in a circle's centre, the angle for a 75° curve is:
5/24 of a complete circle is 75/360.
Therefore, the 75° arc's extent is
5/24 × 6π = 5π/4 ≈ 3.93 feet
To know more about circle visit:
https://brainly.com/question/29142813
#SPJ1
#5) Greg worked these hours last week: Monday, 9; Tuesday, 8 %; Wednesday 9.25; Thursday, 11; and Friday 9 3/4.
He works a 40 hour week with time and a half being paid for overtime work. His regular gross pay rate is $22.25 an hour. What was Greg's gross pay for the week?

Answers
9514 1404 393
Answer:
gross pay: $1131.97
Step-by-step explanation:
Greg's total time for the week is ...
9 +8.25 +9.25 +11 +9.75 = 47.25 . . . . hours
Assuming hours over 40 are overtime hours, this represents ...
47.25 -40 = 7.25 . . . overtime hours
Greg's regular pay is ...
$22.25/h × 40 h = $890 . . . regular pay
Greg's overtime pay is ...
$22.25 × 1.5 × 7.25 = $241.96875 ≈ $241.97 . . . overtime pay
Greg's gross pay is the sum of his regular pay and overtime pay:
gross pay = $890 +241.97 = $1131.97
_____
Alternate solutions
Once we find that Greg's total hours are 47.25, of which 7.25 are overtime hours, we can add half the overtime hours to get 47.25 +(1/2)(7.25) = 50.875. Greg's gross pay will be equivalent to straight-time pay for this number of hours: $22.25 × 50.875 = 1131.96875 ≈ 1131.97.
Yet another way to solve this is to multiply total hours by the overtime pay rate and subtract an amount to make up for the fact that 40 hours are not paid at that rate. If the OT rate is pre-computed, this only takes two mathematical operations: one multiplication and one subtraction.
OT rate = 1.5 × 22.25 = 33.375
gross pay = (47.25 h)×($33.375/h) -445 = $1131.97
If ACD and BAC are alternate interior angles and mACD=101°

Answers
Answer is A. 101°
Step-by-step explanation:
The base of the mountain is 6,500 feet above sea level and AB measures 230 feet across. Given that the measurements for QAP is 20° and QBP is 35°, how far above sea level is peak P ? Express your answer to the nearest foot.
Height above sea level:

Answers
Answer:
6610
Step-by-step explanation:
We have tan(X) = opposite/ adjacent
tan(QBP) = PQ/BQ
tan(35) = PQ/BQ ---eq(1)
tan(QAP) = PQ/AQ
tan(20) = \(\frac{PQ}{AB +BQ}\)
\(=\frac{1}{\frac{AB+BQ}{PQ} } \\\\=\frac{1}{\frac{AB}{PQ} +\frac{BQ}{PQ} } \\\\= \frac{1}{\frac{230}{PQ} + tan(35)} \;\;\;(from\;eq(1))\\\\= \frac{1}{\frac{230 + PQ tan(35)}{PQ} } \\\\= \frac{PQ}{230+PQ tan(35)}\)
230*tan(20) + PQ*tan(20)*tan(35) = PQ
⇒ 230 tan(20) = PQ - PQ*tan(20)*tan(35)
⇒ 230 tan(20) = PQ[1 - tan(20)*tan(35)]
\(PQ = \frac{230 tan(20)}{1 - tan(20)tan(35)}\)
\(= \frac{230*0.36}{1 - 0.36*0.7}\\\\= \frac{82.8}{1-0.25} \\\\=\frac{82.8}{0.75} \\\\= 110.4\)
PQ = 110.4
≈110
Height above sea level = 6500 + PQ
6500 + 110
= 6610
Which linear function has the same y-intercept as the one that is represented by the graph?
On a coordinate plane, a line goes through points (3, 4) and (5, 0).
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 3, negative 1, 1, 3. Column 2 is labeled y with entries negative 4, 2, 8, 14.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 4, negative 2, 2, 4. Column 2 is labeled y with entries negative 26, negative 18, negative 2, 6.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 5, negative 3, 3, 5. Column 2 is labeled y with entries negative 15, negative 11, 1, 5.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 6, negative 4, 4, 6. Column 2 is lab
eled y with entries negative 26, negative 14, 34, 46.
Answers
The linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
To determine the linear function with the same y-intercept as the graph, we need to find the equation of the line passing through the points (3, 4) and (5, 0).
First, let's find the slope of the line using the formula:
slope (m) = (change in y) / (change in x)
m = (0 - 4) / (5 - 3)
m = -4 / 2
m = -2
Now that we have the slope, we can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Using the point (3, 4) as our reference point, we have:
y - 4 = -2(x - 3)
Expanding the equation:
y - 4 = -2x + 6
Simplifying:
y = -2x + 10
Now, let's check the given options to find the linear function with the same y-intercept:
Option 1: The table with x-values (-3, -1, 1, 3) and y-values (-4, 2, 8, 14)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 2: The table with x-values (-4, -2, 2, 4) and y-values (-26, -18, -2, 6)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 3: The table with x-values (-5, -3, 3, 5) and y-values (-15, -11, 1, 5)
The y-intercept is the same as the given line (10). So, this option is correct.
Option 4: The table with x-values (-6, -4, 4, 6) and y-values (-26, -14, 34, 46)
The y-intercept is not the same as the given line. So, this option is not correct.
Therefore, the linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
for such more question on linear function
https://brainly.com/question/9753782
#SPJ8
PLEASE HELP ON QUESTION ASAP! 30PTS!
I WILL ALSO GIVE YOU A THANKS RATE YOU FIVE STARS AND MAYBE EVEN BRAINLIEST any silly answeres will be reported / deleted
Hiba needs 40g sugar to make 15 biscuits. she also needs three times as much flour as sugar . Hiba is going to make 60 biscuits . work out the amount of flour she needs .
Answers
40.3=120g flour➡️15 biscuits
60 biscuits = 16.4➡️120.4 = 480g flour
She needs 480g flour to make 60 biscuits
HELP PLEASE FAST
Find the second differences for the relation.

Answers
The second differences for the relation is -2 which is option A.
What is the second differences for the relation?To find the second differences, we need to calculate the difference between consecutive differences of the 'y' values in the given relation.
First, let's calculate the first differences:
-9 - (-4) = -5
-4 - (-1) = -3
-1 - 0 = -1
0 - (-1) = 1
-1 - (-4) = 3
-4 - (-9) = 5
Now, let's calculate the second differences:
-5 - (-3) = -2
-3 - (-1) = -2
-1 - 1 = -2
1 - 3 = -2
3 - 5 = -2
The second differences for the given relation are all -2.
learn more on relations here;
https://brainly.com/question/29685213
#SPJ1
8.What side of the road will you see speed, yield, and guide signs on ?
Answers
Answer:
we see it in our left side of the road
R 408 344 525.2 What i want to know this money is a millions or thousand?
Answers
Answer:
million
Step-by-step explanation:
need help asap!
Mildred has a circular yard with a diameter of 145 feet
She wants to put a fence around the entire yard. How many feet of fence would it take to put Fence around the entire circular yard?
Answers
Approximately 456.3 feet of fence to surround the entire circular yard.
Now, For the amount of fencing needed to surround a circular yard, we have to calculate the circumference of the circle, which is the distance around the circle.
Since, The circumference of a circle is,
⇒ C = πd,
where, C is circumference, d is diameter,
Here, the diameter of the circular yard is 145 feet,
So the radius is half of that,
r = 145/2 = 72.5 feet.
So, Using the formula, we can calculate the circumference as:
C = πd
C = 3.14 x 145
C = 456.3 feet
Therefore, Approximately 456.3 feet of fence to surround the entire circular yard.
Learn more about the circle visit:
https://brainly.com/question/24810873
#SPJ1
Find the slope of the line
A. -4
B. -1/4
C. 1/4
D. 4

Answers
Answer:
C. 1/4
hopes this helped
to get the equation of any straight line, we simply need two points off of it, let's use those two in the picture below
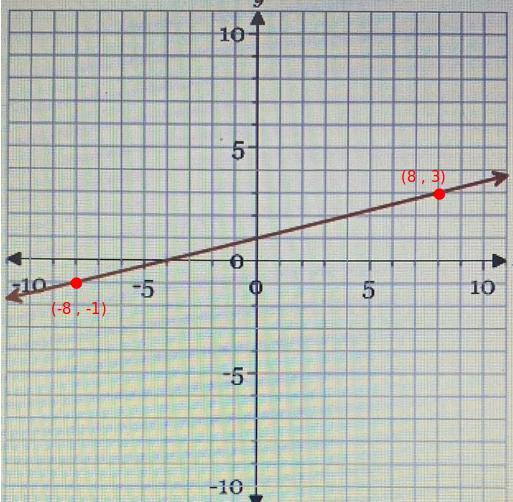
\((\stackrel{x_1}{-8}~,~\stackrel{y_1}{-1})\qquad (\stackrel{x_2}{8}~,~\stackrel{y_2}{3}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{3}-\stackrel{y1}{(-1)}}}{\underset{\textit{\large run}} {\underset{x_2}{8}-\underset{x_1}{(-8)}}} \implies \cfrac{3 +1}{8 +8} \implies \cfrac{ 4 }{ 16 } \implies \cfrac{1 }{ 4 }\)
The figure above shows a store's supply-demand graph for coffee makers. If the store sells $600 worth of coffee makers, which of the following is a valid possible price for them?
A. $15
B. $30
C. $40
D. $55

Answers
The possible price for the items if the store sells $600 is (c) $40
How to determine the possible price for the items?From the question, we have the following parameters that can be used in our computation:
The supply-demand graph
If the store sells $600, then there is a supply worth of $600
The equation of the supply line is calculated as
y = mx + c
Where
c = y = 0
i.e. c = 100
So, we have
y = mx + 100
Using another point on the graph, we have
30m + 10 = 400
So, we have
m = 13
This means that
y = 13x + 100
For a supply of 600, we have
13x + 100 = 600
So, we have
13x = 500
Divide by 13
x = 38.4
Approximate
x = 40
Hence, the possible price for the items is (c) $40
Read more about supply-demand graph at
https://brainly.com/question/14297698
#SPJ1
It has been said that only the top 2% of athletes will go pro. What Z-Score is required to be the top 2%?
Round to 2 decimal places.
Answers
If the top 2% of athletes will go pro, then the Z-Score that is required to be 0.0438.
In this question, we have been that the top 2% of athletes will go pro.
We are required to find the Z-Score that is required to be the top 2%.
Because only 2% of the top is pro then it will be a two tailed test.
The required percentage will be 2/2=1%
The value which we will require to catch up from table = 0.01
Z value = 0.0438
Therefore, if the top 2% of athletes will go pro, then the Z-Score that is required to be 0.0438.
Learn more about the z-score here:
brainly.com/question/25638875
#SPJ1
Allison and Sean were splitting nachos. If Allison ate 5/12 of the nachos and Sean ate 1/5 of the nachos, what fraction of the nachos did they eat together?
Answers
Answer:
thank for points
Step-by-step explanation:
Answer:
37/60
Step-by-step explanation:
Because 5/12+1/5=37/60
A new drug on the market is known to cure 30% of patients with cervical cancer. If a group of 18 patients is randomly selected, what is the probability of observing, at most, one patient who will be cured of cervical cancer?
Answers
Answer:
Probability cured of cervical cancer = 18C0 (0.30)⁰(0.70)¹⁸ + 18C1(0.30)(0.70)¹⁷
Step-by-step explanation:
Given:
Patients cured = 30% = 0.30
Number of patients (n) = 18
Probability cured of cervical cancer = P(X≤1)
Probability cured of cervical cancer = P(X=0) + P(X=1)
Probability cured of cervical cancer = 18C0 (0.30)⁰(0.70)¹⁸ + 18C1(0.30)(0.70)¹⁷