In 2016 there were approximately 7,040 college and university libraries in the United States. A survey found that 65% of those libraries participated in an electronic "book-sharing" program. Based on this information, how many college and university libraries participated in the electronic "book-sharing" program in 2016?
Answers
To calculate the approximate number of libraries that participated in the book-sharing program in 2016, we multiply the total number of college and university libraries (7,040) by the percentage of libraries participating (65%).
By multiplying 7,040 by 0.65, we find that approximately 4,576 libraries participated in the book-sharing program in 2016.
This calculation assumes that the percentage given accurately represents the proportion of libraries participating in the program. However, it's important to note that this is an approximation based on the given information. The actual number of participating libraries may vary slightly due to factors such as reporting discrepancies or changes in participation rates over time.
Learn more about book-sharing: https://brainly.com/question/24877689
#SPJ11
Related Questions
If an automobile slows from 26 m/s 18 m/s in the period of 4.0 s what was the average acceleration
Answers
Answer: -2
Step-by-step explanation:
The statement "P implies Q' is FALSE under which of the following conditions? Choose all that apply. a. P and Q are both true. b. P and Q are both false. c. P is true and Q is false. d. P is false and Q is true.
Answers
The statement "P implies Q" is false under the following conditions: a) P is true and Q is false, and d) P is false and Q is true.
The statement "P implies Q" can be expressed as "if P, then Q." It is a conditional statement where P is the antecedent (the condition) and Q is the consequent (the result).
To determine when the statement is false, we need to identify cases where P is true but Q is false, or when P is false but Q is true.
Option a) states that both P and Q are true. In this case, the statement "P implies Q" holds true because if P is true, then Q is true.
Option b) states that both P and Q are false. In this case, the statement "P implies Q" is considered true because the antecedent (P) is false.
Option c) states that P is true and Q is false. Under this condition, the statement "P implies Q" is false because when P is true, but Q is false, the implication does not hold.
Option d) states that P is false and Q is true. In this case, the statement "P implies Q" is true because the antecedent (P) is false.
Therefore, the conditions under which the statement "P implies Q" is false are a) P is true and Q is false, and d) P is false and Q is true.
Learn more about conditional statement here:
https://brainly.com/question/30612633
#SPJ11
Construct a table of values for the following equation as shown. \( x=y+2 \) for integral values of \( y \) from \( -2 \) to \( +6 \) Complete the following table of values.
Answers
To construct a table of values for the equation \( x=y+2 \) for integral values of \( y \) from -2 to +6, we can substitute each value of \( y \) into the equation and solve for \( x \).
Here is the completed table of values:
\[
\begin{array}{|c|c|}
\hline
\text{Value of } y & \text{Value of } x \\
\hline
-2 & -2+2=-0 \\
-1 & -1+2=1 \\
0 & 0+2=2 \\
1 & 1+2=3 \\
2 & 2+2=4 \\
3 & 3+2=5 \\
4 & 4+2=6 \\
5 & 5+2=7 \\
6 & 6+2=8 \\
\hline
\end{array}
\]
we substituted the values of \( y \) from -2 to +6 into the equation \( x=y+2 \) and obtained the corresponding values of \( x \) to complete the table. This shows the relationship between \( x \) and \( y \) for the given equation.
To know more about integral values , visit ;
https://brainly.com/question/33441261
#SPJ11
11) Calculate the total volume of the composite object.

Answers
The total volume of the composite object is 838.095
Calculating the total volume of the composite object.From the question, we have the following parameters that can be used in our computation:
The composite object
The volume is calculated as
Volume = Cylinder + Cube
The Cylinder and the Cube have the same dimensions
So, we have
V = 4/3πr²h
Substitute the known values in the above equation, so, we have the following representation
V = 4/3 * 22/7 * 5² * 8
Evaluate
V = 838.095
Hence, the total volume of the composite object is 838.095
Read more about volume at
https://brainly.com/question/30849227
#SPJ1
please help me please

Answers
Answer:
Answer is a.multiplication.
Step-by-step explanation:
I hope it's helpful!
You spin once find the p(spin a number less than 3 or a 5) =You spin twice find the p(spin even number and then a number greater than 3) =

Answers
Before we begin analyzing the question we were asked, we need to compute the probabilities of getting the individual numbers on the spinner out of a total of 12 slots.
Probability of getting a 1:
There is only a single value of 1, therefore the probability of getting a 1 is:
\(P(\text{getting 1)=}\frac{1}{12}\)Probability of getting a 2:
There are double values of 2, therefore the probability of getting a 2 is:
\(P(\text{getting 2)=}\frac{2}{12}=\frac{1}{6}\)Probability of getting a 3:
There are triple values of 3, therefore the probability of getting a 3 is:
\(P(\text{getting 3)=}\frac{3}{12}=\frac{1}{4}\)Probability of getting a 4:
There are double values of 4, therefore the probability of getting a 4 is:
\(P(\text{getting 4)=}\frac{2}{12}=\frac{1}{6}\)Probability of getting a 5:
There are 4 values of 5, therefore the probability of getting a 5 is:
\(P(\text{getting 5)=}\frac{4}{12}=\frac{1}{3}\)Now that we know the probabilities of getting the individual numbers we can proceed to solving the questions asked.
A number less than 3 or a 5:
The only numbers less than 3 are: 1 and 2.
Since the spinner is spun just once, it means that, if we are to get a number less than 3, then we get either 1 OR 2.
The probability for getting a 1 OR a 2 is:
\(\begin{gathered} P(1\text{ OR 2)= P(getting 1) + P(getting 2)} \\ P(1\text{ OR 2) = }\frac{1}{12}+\frac{1}{6} \\ P(1\text{ OR 2)=}\frac{1}{4} \end{gathered}\)But the question goes on and says in the same trial, what is the possibility of also getting a 5.
This means we can rephrase the question as:
Probability of getting 1 OR 2 OR 5.
Therefore, to fully answer the first question, we say:
\(\begin{gathered} P(\text{less than 3 or a 5)=P(1 OR 2 OR 5) = P(1 OR 2) + P(a 5)} \\ P(\text{less than 3 or a 5)=}\frac{1}{4}+\frac{4}{12} \\ \\ P(\text{less than 3 or a 5)=}\frac{7}{12} \end{gathered}\)The probability of getting a number less than 3 or a 5 is 7/12
Now for the next question;
Spin Even number and then number greater than 3:
To get an even number you can have only: 2 and 4
The question says you spin twice and asks for the probability in which the first number is even. This means the first number is Either 2 OR 4 not both.
We can compute this probability as:
\(\begin{gathered} P(2\text{ OR 4)=P(2) + P(4)} \\ P(2\text{ OR 4) = }\frac{2}{12}+\frac{2}{12} \\ \\ \therefore P(2\text{ OR 4)=}\frac{1}{3} \end{gathered}\)The question also says the second number is a number greater than 3. The only numbers greater than 3 are: 4 and 5.
The second number can be Either 4 OR 5
We can compute this probability as:
\(\begin{gathered} P(4\text{ OR 5)=P(4) + P(5)} \\ P(4\text{ OR 5) = }\frac{2}{12}+\frac{4}{12} \\ \\ P(4\text{ OR 5)=}\frac{1}{2} \end{gathered}\)Now that we have both probabilities for the first spin and the second spin, we can therefore calculate for when you get:
Even number AND Number greater than 3
\(\begin{gathered} P(2\text{ OR 4) AND P(4 OR 5)= P(2 OR 4) }\times P(4\text{ OR 5)} \\ \frac{1}{3}\times\frac{1}{2}=\frac{1}{6} \end{gathered}\)Therefore the probability of getting Even number and number greater than 3 is: 1/6
The final answer is:
#1: 7/12
#2: 1/6
Ommy paid $39 to fill up the gas tank in his car. If one gallon of gas costs $3, how many gallons of gas did Tommy put in?
Answers
Kevin took his car to Dwain's Automotive to have the engine replaced. Kevin was
told that at the most, the total bill for parts and labor would be $6,300. The cost of
the parts was $3,900. How much could Kevin expect to pay for labor?
Answers
Answer:
Step-by-step explanation:
$2400 in labor
Hanson has 38 pieces of candy. He gives away c of the pieces. Write an expression that
shows the number of pieces of candy Hanson has left.
Answers
Answer:
38-c
Step-by-step explanation:
We know that the answer is 38-c because any piece of candy that Hanson gives away will be subtracted from the amount that he started out with.
Finding probability, please help!! show all work!!

Answers
Answer:
9/28 and 32.1%
Step-by-step explanation:
So the sample space consists of all products for (5 * 1, 5 * 2, 5 * 3.... and the same thing for 6, 7, and 8)
This gives you the sample space: {5, 10, 15, 20, 25, 30, 6, 12, 18, 24, 30, 36, 7, 14, 21, 28, 35, 42, 8, 16, 24, 32, 40, 48}.
The size of the sample space is 4 * 6, since for each number (5, 6, 7, 8), there are 6 products (the dice have six numbers). This means the sample space has 24 combinations, you can also verify this by manually counting the sample space.
Now filtering the sample space so you only get a product that is 28 or higher you get: {30, 30, 36, 28, 35, 42, 32, 40, 48} which has 9 possible combinations that have a product greater than or equal to 28. Divide this by the entire sample space and you get a probability of: 9/28, which in decimal form is approximately: \(0.3214\). Multiplying this by 100 gives you: \(32.1\)%
NEED HELP! WORTH 27 POINTS!!!!!!

Answers
Just plug -2 into x
f(-2) = 2(-2)^2 + 4(-2) + 5
Simplify the right side
f(-2) = 8 - 8 + 5
Combine like terms
f(-2) = 5
Complete the proof of the identity by choosing the Rule that justifies each step. cos²x(1 + tan’x) = 1 To see a detailed description of a Rule, select the More Information Button to the right of th Statement Rule cos?x(1 + tanx) = cosx (secºx) Rule ? = COS X Rule ? COS X = 1 Rule ? ?
Answers
The proof of the identity cos²x(1 + tan²x) = 1 is complete using the mentioned rules.
Complete the proof of the identity cos²x(1 + tan²x) = 1?Hi! I'd be happy to help you complete the proof of the identity cos²x(1 + tan²x) = 1 using the given terms.
1. Statement: cos²x(1 + tan²x) = cosx (sec²x)
Rule: Identity (using the identity tan²x = sec²x - 1)
2. Statement: cosx (sec²x) = cosx (1 + cos²x)
Rule: Identity (using the identity sec²x = 1/cos²x)
3. Statement: cosx (1 + cos²x) = cos²x + cos⁴x
Rule: Distributive Property (cosx * 1 + cosx * cos²x)
4. Statement: cos²x + cos⁴x = 1
Rule: Pythagorean Identity (since cos²x + sin²x = 1, we substitute sin²x with 1 - cos²x and simplify)
So, the proof of the identity cos²x(1 + tan²x) = 1 is complete using the mentioned rules.
Learn more about identity
brainly.com/question/6971003
#SPJ11
You are given a triangle that has sides 5 7 ad 10 how large is the smallest angle of the triangle
Answers
Answer:
Step-by-step explanation:
Comment
This uses the cosine Law for line length.
Formula
a^2 = b^2 + c^2 - 2*b*c*sin(A)
Givens
a = 5
b = 7
c = 10
Solution
5^2 = 7^2 + 10^2 - 2*7*10*cos(A)
25 = 49 + 100 - 140*cos(A) Combine the right side
25 = 149 - 140 * cos(A) Subtract 149 from both sides
25 - 149 = - 140*cos(A)
-124 = -140 * cos(A) Divide both sides by -140
-124/-140 = cos(A)
Cos(A) = 0.8857 Take the inverse Cos of both sides
A = cos-1(0.8857)
Answer
A = 27.66 degrees
(PLEASE HELP ME I BEG OF YOU)
Kevin and cannot eat on $135 a month salary there any commission for each sale they make and the ratio of Kevin and Kenneth commission is 3:4 if they sell Products worth $610 each in March and Kevin Owens at 12% commission how much did each of them??
A. Kenneth makes $232.60
B. Kevin makes $208.20
C. Kevin makes $73.20
D. They both make $440.00
E. Kenneth makes $219.60
Answers
Answer:
I think the asnwer A or B !!
Step-by-step explanation:
Suppose a 95% confidence interval for the average amount of weight loss on a diet program for males is between 13. 4 and 18. 3 pounds. These results were based on a sample of 42 male participants who were deemed to be overweight at the start of the 4-month study. What is the standard error of the sample mean?.
Answers
The standard error of the sample mean is 1.21.
Given;
Suppose a diet regimen for men results in an average weight loss of between 13. 4 and 18. 3 pounds, according to a 95% confidence interval. These findings were based on a group of 42 men who were classified as overweight at the beginning of the four-month trial.
A 95% confidence interval for a population mean is (13.4, 18.3)
Upper limit = 18.3
Lower limit = 13.4
Since population SD is unknown, this interval is constructed using the t distribution.
n = 42
c = 0.95
∴ α = 1 - c = 1 - 0.95 = 0.05
α/2 = 0.025
Also, d.f = n - 1 = 42 - 1 = 41
∴ ta/2.d.f = ta/2.n-1 = t0.025,41 = 2.02 . . . . use t table
Now,
The margin of error = (Upper limit - Lower limit)/2
= (18.3 - 13.4)/2
= 2.45
But,
Margin of error = ta/2.d.f- * (s / \sqrt{} n)
Margin of error = ta/2.d.f- * Standard error
2.45 = 2.02 * Standard error
Standard error = 1.2129
To learn more about Margin of error click here:
brainly.com/question/10501147
#SPJ4
4+y+7 what’s the answerrr
Answers
Answer: y + 11
Step-by-step explanation:
1. Combine like terms
=4+y+7
=(y)+(4+7)
=y+11
Answer:
y + 11
Step-by-step explanation:
4 + y + 7
y + 4 + 7
y + (4 + 7)
y + 11
I hope this helps you :)
The number n is doubled and then has y added to it. The result is then divided by 2 and has the number n subtracted from it, the final result is
Answers
Answer:
\(\frac{y}{2}\)
Step-by-step explanation:
n is doubled: 2n
y added: 2n + y
divided by 2: n + \(\frac{y}{2}\)
n subtracted -> final resutl: \(\frac{y}{2}\)
Identify the type of slope each line has
Pls help me ;-;
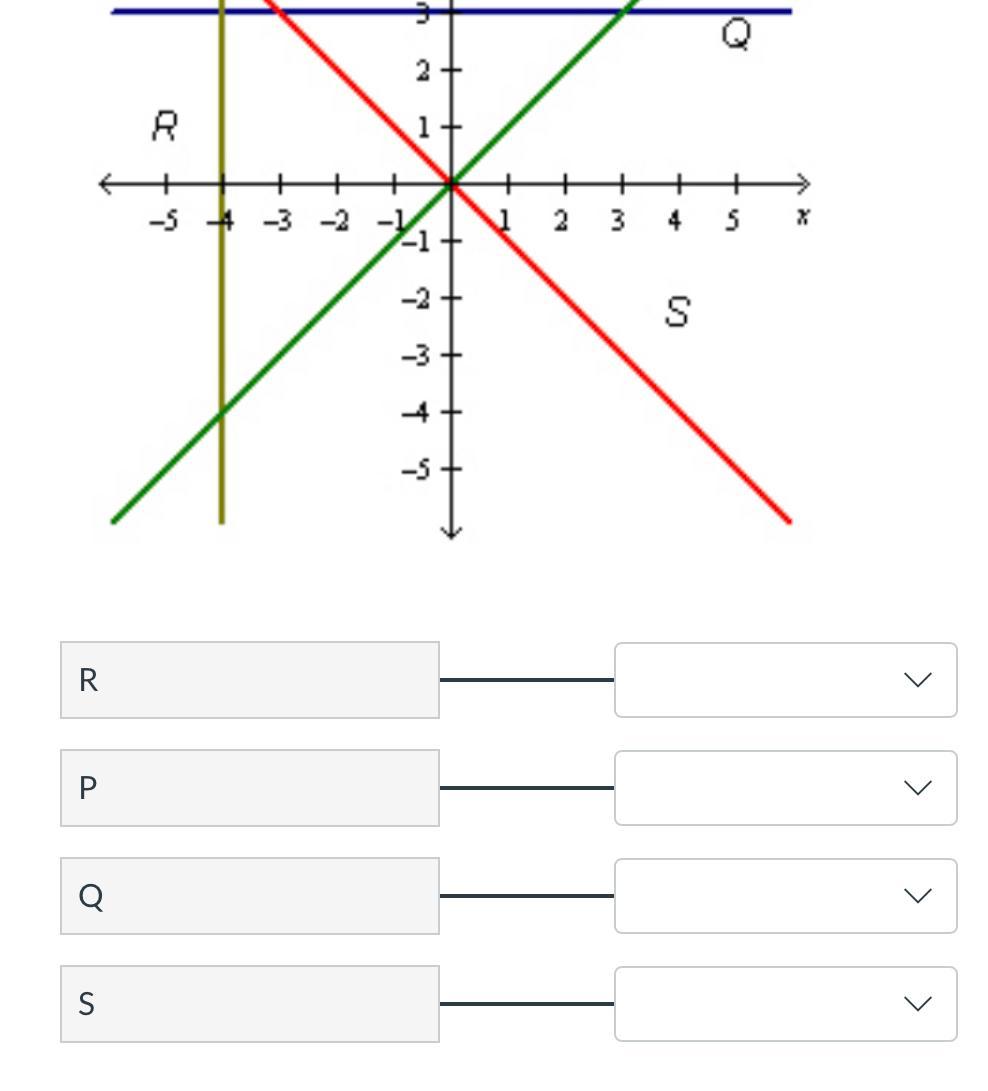


Answers
Answer:
hi
Step-by-step explanation:
⠀⠀⠀⠀⠀⠀⣤⣶⣶
⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣀⣀
⠀⠀⠀⠀⠀⣀⣶⣿⣿⣿⣿⣿⣿
⣤⣶⣀⠿⠶⣿⣿⣿⠿⣿⣿⣿⣿
⠉⠿⣿⣿⠿⠛⠉⠀⣿⣿⣿⣿⣿
⠀⠀⠉⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣤⣤
⠀⠀⠀⠀⠀⠀⠀⣤⣶⣿⣿⣿⣿⣿⣿
⠀⠀⠀⠀⠀⣀⣿⣿⣿⣿⣿⠿⣿⣿⣿⣿
⠀⠀⠀⠀⣀⣿⣿⣿⠿⠉⠀⠀⣿⣿⣿⣿
⠀⠀⠀⠀⣿⣿⠿⠉⠀⠀⠀⠀⠿⣿⣿⠛
⠀⠀⠀⠀⠛⣿⣿⣀⠀⠀⠀⠀⠀⣿⣿⣀
⠀⠀⠀⠀⠀⣿⣿⣿⠀⠀⠀⠀⠀⠿⣿⣿
⠀⠀⠀⠀⠀⠉⣿⣿⠀⠀⠀⠀⠀⠀⠉⣿
⠀⠀⠀⠀⠀⠀⠀⣿⠀⠀⠀⠀⠀⠀⣀⣿
⠀⠀⠀⠀⠀⠀⣀⣿⣿
⠀⠀⠀⠀⠤⣿⠿⠿⠿ ⠀⠀⠀⠀⣀
⠀⠀⣶⣿⠿⠀⠀⠀⣀⠀⣤⣤
⠀⣶⣿⠀⠀⠀⠀⣿⣿⣿⠛⠛⠿⣤⣀
⣶⣿⣤⣤⣤⣤⣤⣿⣿⣿⣀⣤⣶⣭⣿⣶⣀
⠉⠉⠉⠛⠛⠿⣿⣿⣿⣿⣿⣿⣿⠛⠛⠿⠿
⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⠿
⠀⠀⠀⠀⠀⠀⠀⠿⣿⣿⣿⣿
⠀⠀⠀⠀⠀⠀⠀⠀⣭⣿⣿⣿⣿⣿
⠀⠀⠀⠀⠀⠀⠀⣤⣿⣿⣿⣿⣿⣿
⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⠿
⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⠿
⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿
⠀⠀⠀⠀⠀⠀⠀⠉⣿⣿⣿⣿
⠀⠀⠀⠀⠀⠀⠀⠀⠉⣿⣿⣿⣿
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠉⣿⠛⠿⣿⣤
⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⣿⠀⠀⠀⣿⣿⣤
⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⠀⠀⠀⣶⣿⠛⠉
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿
⠀⠀⣶⠀⠀⣀⣤⣶⣤⣉⣿⣿⣤⣀
⠤⣤⣿⣤⣿⠿⠿⣿⣿⣿⣿⣿⣿⣿⣿⣀
⠀⠛⠿⠀⠀⠀⠀⠉⣿⣿⣿⣿⣿⠉⠛⠿⣿⣤
⠀⠀⠀⠀⠀⠀⠀⠀⠿⣿⣿⣿⠛⠀⠀⠀⣶⠿ no
⠀⠀⠀⠀⠀⠀⠀⠀⣀⣿⣿⣿⣿⣤⠀⣿⠿
⠀⠀⠀⠀⠀⠀⠀⣶⣿⣿⣿⣿⣿⣿⣿⣿
⠀⠀⠀⠀⠀⠀⠀⠿⣿⣿⣿⣿⣿⠿⠉⠉
⠀⠀⠀⠀⠀⠀⠀⠉⣿⣿⣿⣿⠿
⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⠉
⠀⠀⠀⠀⠀⠀⠀⠀⣛⣿⣭⣶⣀
⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿
⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⠉⠛⣿
⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⠀⠀⣿⣿
⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣉⠀⣶⠿
⠀⠀⠀⠀⠀⠀⠀⠀⣶⣿⠿
⠀⠀⠀⠀⠀⠀⠀⠛⠿⠛no
I need help with this geometry equation

Answers
The area of the composite figure is 58. 71 square units.
How to determine the areaIt is important to note that the area of the composite figure is given as;
Area of a rectangle + area of a semi circle
The formula for area of a rectangle is expressed as;
Area = lw
Where;
l is the length of the rectanglew is the width of the rectangleNow, let's substitute the values, we have;
Area = 6 × 9
Area = 54 square units
The formula for area of a semicircle is expressed as;
Area = πr²/2
Where;
pi = 3. 14r is the radius of the semi circleGiven diameter = 6, radius = 6/2 = 3
Substitute the value
Area = 3. 14(3)/2
Area = 4. 71 square units
But area of the composite figure = 54 + 4. 71 = 58. 71 square units.
Hence, the area is 58. 71 square units.
Learn more about area here:
https://brainly.com/question/25292087
#SPJ1
PLEASE HELP ASAP!!! Two weeks in a row, the golf course hosts a group of golfers. The second week had 10 more golfers than the first week. Use the dot plots to choose the true statement.
dot plot titled Number of Golfers for Week 1 with number line labeled Age of Golfer, 1 dot at 62, 3 dots at 68, 1 dot at 69, 2 dots at 70, 3 dots at 72, 2 dots at 75, 1 dot at 76, 2 dots at 78, 3 dots at 80, and 2 dots at 89
dot plot titled Number of Golfers for Week 2 with number line labeled Age of Golfer, 3 dots at 62, 4 dots at 63, 2 dots at 64, 1 dot at 66, 1 dot at 67, 3 dots at 68, 1 dot at 69, 2 dots at 70, 3 dots at 72, 2 dots at 75, 1 dot at 76, 2 dots at 78, 3 dots at 80, and 2 dots at 89
A) The range for Week 1 equals the range for Week 2.
B) The range for Week 1 is greater than the range for Week 2.
C) The median for Week 1 is less than the median for Week 2.
D) The mean for Week 1 is greater than the mean for Week 2.
Answers
The true statement is the range for Week 1 equals the range for Week 2.
What is the true statement?A dot plot is a graph that is used to show the frequency of a data set using dots. Range is the difference between the highest and lowest values of a set of observations
Range = highest value - lowest value
Range of the first dot plot : 89 - 62 = 27
Range of the second dot plot : 89 - 62 = 27
To learn more about range, please check: https://brainly.com/question/12372689
#SPJ1
What is the equation of the line that passes through the point (8,6) and has a slope of 1/4?
Answers
Answer:
y=1/4x+4
Step-by-step explanation:
because the slope is 1/4
so k=1/4
y=1/4x+b
put the point into the equation
so
6=1/4*8+b
so
b=4
What is 17,683 rounded to the nearest ten thousand?
Answers
20,000
Thankyou :)
Follow me....
Which expression converts 100 inches per minute to feet per minute?
100 Inches
I minute
60 minutes
1 hour
100 inches
1 minute
1 hour
60 minutes
100 inches
1 minute
1 foot
12 inches
100 inches
1 minute
12 inches
1 foot
Answers
Recursively computing sums of cubes, cont.G About (a) Use induction to prove that the algorithm to compute the sum of the cubes of the first n positive integers (shown below) returnsthe correct value for every positive integer input.SumCube(n)Input: A positive integer n.Output: 1^3 + 2^3 + ... + n^3.If (n = 1), Return (1)s := SumCube(n - 1) // The recursive callReturn (n3 + s)
Answers
By the principle of mathematical induction, we will show that the algorithm to compute the sum of the cubes of the first n positive integers returns the correct value for every positive integer input.
To prove that the algorithm to compute the sum of the cubes of the first n positive integers returns the correct value for every positive integer input using induction, we will need to show two things:
1. Base case: The algorithm returns the correct value for n = 1.
Base case: When n = 1, the algorithm returns 1^3, which is the correct value for the sum of the cubes of the first positive integer. Therefore, the base case is true.
2. Inductive step: Assume that the algorithm returns the correct value for some positive integer k, and show that it also returns the correct value for k + 1.
Inductive step: Assume that the algorithm returns the correct value for some positive integer k, i.e., SumCube(k) returns 1^3 + 2^3 + ... + k^3.
We need to show that the algorithm also returns the correct value for k + 1, i.e., SumCube(k + 1) returns 1^3 + 2^3 + ... + (k + 1)^3.
Using the recursive definition of the algorithm, we have:
SumCube(k + 1) = (k + 1)^3 + SumCube(k)
By the induction hypothesis, we know that SumCube(k) returns the correct value, so we can substitute it into the above equation to get:
SumCube(k + 1) = (k + 1)^3 + (1^3 + 2^3 + ... + k^3)
Expanding (k + 1)^3, we get:
SumCube(k + 1) = k^3 + 3k^2 + 3k + 1 + (1^3 + 2^3 + ... + k^3)
Simplifying the right-hand side, we get:
SumCube(k + 1) = 1^3 + 2^3 + ... + k^3 + (k^3 + 3k^2 + 3k + 1)
We recognize the last term as (k + 1)^3, so we can substitute it in to get:
SumCube(k + 1) = 1^3 + 2^3 + ... + k^3 + (k + 1)^3
which is the correct value for the sum of the cubes of the first (k + 1) positive integers. Therefore, the inductive step is true.
By the principle of mathematical induction, we have shown that the algorithm to compute the sum of the cubes of the first n positive integers returns the correct value for every positive integer input.
To know more about mathematical induction refer here :
https://brainly.com/question/31244444#
#SPJ11
What is the equation of the following graph in vertex form?
(-1,0)
-1
Courtesy of Texas Instruments
(0, 1)

Answers
The equation of the graph of the quadratic function is the option;
y = (x + 1)²
What is a quadratic function?A quadratic function is a function of the form; f(x) = a·x² + b·x + c, where a ≠ 0, and a, b, and c are numbers.
The shape of the graph indicates that the graph is a quadratic function
The x and y-intercepts of the function are;
x-intercept = (0, -1)
y-intercept = (0, 1)
The x-intercept indicates that when x = -1, y = 0
The y-intercept indicates that when y = 1, x = 0
The number of x-intercepts, which is one, indicates that the possible number of solutions is one and therefore, the function is a perfect square of the form; y = (x + 1)²
The above function can be obtained from the standard form of the quadratic equation; f(x) = a·(x - h)² + k
(h, k) = The coordinates of the vertex
a = The leading coefficient
The vertex of the graph is; (-1, 0)
Therefore;
h = -1, and k = 0
f(x) = y = a·(x - (-1))² + 0 = a·(x + 1)²
y = a·(x + 1)²
When y = 1, x = 0, therefore;
y = a·(0 + 1)² = 1
a = 1/1 = 1
a = 1
y = a·(x + 1)² = 1 × (x + 1)² = (x + 1)²
y = (x + 1)²
Learn more on the graph of quadratic functions here: https://brainly.com/question/10441997
#SPJ1
Dusty has a summer lawn-mowing business. In one week, he mows 20 lawns and earns a total of $450. If he charges the same amount for each lawn, how much does Dusty charge to mow a lawn?
Answers
Answer:
Step-by-step explanation:
Write in slope-intercept form,
y=mx + b. − mowing, week, 20, 450
1 A home improvement store purchases $300 worth of materials. They charge a 55% markup. For how much will the materials be sold?
Answers
(300*1.55)
which two points lie on a line with a slope closest to zero ?

Answers
Answer:
Point N and point K
Step-by-step explanation:
The steeper a line is in the graph, the greater the value of the slope of the line would be, and also, the farther it would be from 0. On the other hand, the more gentle and less sloppy a line is, the smaller the value of the slope is, and also, the closer it is to 0.
From the graph given, there are possible set of points in a line that have a gentle line slope.
The first is, points N and K. The slope of this line is ⅑.
The second is, points P and L. The slope of this line is ⅙.
From the two above lines, the one with a slope closest to 0 is the line that runs through points N and K. ⅑ is closer to 0 than ⅙.
An Alligator is laying out next to a perfectly circular pond. He is 45 feet from the edge of the pond and 65 feet from the point of tangency. Determine the radius of the pond. Round to the nearest tenth
Answers
The radius of the pond is approximately 33.5 feet if he is 45 feet from the edge of the pond and 65 feet from the point of tangency.
Let's consider the scenario. We have an alligator laying out next to a perfectly circular pond. The alligator is 45 feet from the edge of the pond and 65 feet from the point of tangency.
To find the radius of the pond, we can create a right triangle using the alligator, the point of tangency, and the center of the pond. The line connecting the alligator to the point of tangency is perpendicular to the radius of the pond.
We can use the Pythagorean theorem to solve for the radius. The hypotenuse of the right triangle is the distance between the alligator and the point of tangency, which is 65 feet. One of the legs is the radius of the pond, and the other leg is the distance between the alligator and the edge of the pond, which is 45 feet.
Applying the Pythagorean theorem:
r^2 + 45^2 = 65^2
r^2 + 2025 = 4225
r^2 = 4225 - 2025
r^2 = 2200
Taking the square root of both sides:
r ≈ √2200
r ≈ 46.9
Rounding to the nearest tenth:
r ≈ 33.5
The radius of the pond is approximately 33.5 feet.
To know more about radius, visit
https://brainly.com/question/27696929
#SPJ11
Solve the inequality 18<-3(4x-2)

Answers
Answer:
Choice 1
Step-by-step explanation:
Answer:
x<-1 and Number 1
Step-by-step explanation:
:)