if you see this pls help with all the geometry questions i've just posted pls i need help

Answers
Answer:
98 looks about right to me
Answer:
C
Step-by-step explanation:
Related Questions
Qué significa a^2 en matemáticas es la mi trabajo
Answers
In mathematics, "\(a^2\)" denotes the square of a number or variable "a." It is calculated by multiplying "a" by itself.
How to illustrate with an example4For example, if "a" is 5, then a^2 would be 5*5, which equals 25. When "a" represents a positive number, its square is always positive.
If "a" is negative, its square is still positive since a negative multiplied by a negative results in a positive.
In geometrical terms, if "a" represents the length of the side of a square, then a^2 represents the area of that square. This notation is part of the general concept of exponentiation.
Read more about exponents here:
https://brainly.com/question/13669161
#SPJ1
The Question in English
What does a^2 mean in mathematics
Find the lower quartile of this data set: 593, 588, 540, 434, 420, 398, 390, 375
420
564
394
427
alsoo im like rly booorrredddd any one wanna talk??
female 14 bdays todayy!!!
Answers
Answer:
Quartiles Quartiles:
Q1 --> 396
Q2 --> 423.5
Q3 --> 552
Step-by-step explanation:
Mean x¯¯¯ 461.91666666667
Median x˜ 423.5
Mode 420
Range 218
Minimum 375
Maximum 593
Count n 12
Sum 5543
Quartiles Quartiles:
Q1 --> 396
Q2 --> 423.5
Q3 --> 552
Interquartile
Range IQR 156
Outliers none
Using the given points and line, determine the slope of the line.
(-3, 0) and (2, 7)
slope = -5/7
slope = 7/5
slope = -7/5
slope = 7/5

Answers
Answer:
7/5
Step-by-step explanation:
Slope formula = (y₂ - y₁) / (x₂ - x₁)
= (7 - 0) / (2 - (-3))
= 7 / (2 + 3)
= 7/5
Answer:
7/5
Step-by-step explanation:
We can use the slope formula
m = (y2-y1) / (x2-x1)
= (7-0)/(2 - -3)
= 7/ (2+3)
= 7/5
How many lengths did secretariat win the belmont stakes by
Answers
Secretariat won the Belmont Stakes by a record-breaking 31 lengths.
Secretariat's victory in the 1973 Belmont Stakes is considered one of the most remarkable performances in horse racing history. The legendary racehorse won by an astonishing 31 lengths, establishing a new record that still stands today.
Secretariat's dominant performance captivated audiences as he pulled away from the rest of the field and crossed the finish line in a time of 2 minutes and 24 seconds. This extraordinary margin of victory showcased Secretariat's exceptional speed, stamina, and sheer dominance, solidifying his status as one of the greatest racehorses of all time.
His record-breaking win in the Belmont Stakes remains a defining moment in the sport of horse racing.
To learn more about Belmont Stakes click here: brainly.com/question/13956045
#SPJ11
Find the period of the function f(x) = cos(2.22x+0.19). Provide four decimal places. Answer:______ Find the period of the function f(x) = sin(1.05x). Provide four decimal places. Answer:______
Answers
The period of the function f(x) = cos(2.22x+0.19) is 2.8323 and the period of the function f(x) = sin(1.05x) is 5.9834
The period of a trigonometric function, we use the formula:
Period = 2π/|B|
where B is the coefficient of x in the function.
For the first function, f(x) = cos(2.22x+0.19), the coefficient of x is 2.22. Therefore, the period is:
Period = 2π/|2.22| ≈ 2.8323
For the second function, f(x) = sin(1.05x), the coefficient of x is 1.05. Therefore, the period is:
Period = 2π/|1.05| ≈ 5.9834
So, the period of the first function is 2.83 and the period of the second function is 5.98. Both answers are rounded to four decimal places.
To know more about period of a trigonometric function refer here:
https://brainly.com/question/28483432
#SPJ11
Linda tossed a fair coin 6 times, and the result was heads each time. Which statement
describes the probability of obtaining tails on the 7th toss? (TEKS G.13C-R)
A
Tails is more probable than heads because so far she has tossed only heads.
B
Tails is not probable at all because only heads have come up so far.
C Tails is less probable than heads because each result depends on the previous result.
D Heads or tails is equally probable because each toss is independent.
Answers
Answer:
D.
Step-by-step explanation:
Each toss is independent so the probability of getting a tail is the same thE OF GETTING A HEAD - 50%^.
A pebble is tossed into the air from the top of a cliff. The height of the pebble over time is modeled by the equation y = -16x2 + 32x + 80. What is the maximum height, in feet, reached by the pebble?
Answers
In linear equation, x = 1 is the maximum height, in feet, reached by the pebble.
What in mathematics is a linear equation?
A linear equation is a first-order (linear) term plus a constant in the algebraic form y=mx+b, where m is the slope and b is the y-intercept.
Sometimes, the aforementioned is referred to as a "linear equation of two variables," where x and y are the variables.
The height of the pebble over time is modeled by the equation
y = -16x2 + 32x + 80
At the maximum height, the final velocity of the pebble is zero.
The velocity of the pebble will be obtained by taking the derivative of the given equation.
That is
y' = dy/dx
= d/dx (-16x2 + 32x + 80 )
= -32x + 32
At the maximum height, y' = 0 .
So,
-32x + 32 = 0
32x = 32
x = 32/32
x = 1
Learn more about linear equation
brainly.com/question/11897796
#SPJ4
A train travels from Washington DC to new york(225 miles). The train departs at 4:55 PM and arrives in New York at 7:55 PM. What is the average speed of the train in miles per hour?
Answers
Answer:
The average speed is:
\(\var{v}=75\: miles/h\)
Step-by-step explanation:
The average speed equation is given by:
\(\var{v}=\frac{\Delta x}{\Delta t}\)
Were:
Δx is the displacement (225 miles)Δt is the change in time (3 hours)Then we have:
\(\var{v}=\frac{225}{3}\)
\(\var{v}=75\: miles/h\)
I hope it helps you!
find the volume of the solid enclosed by the surface z − 1 1 x 2 yey
Answers
The volume of the solid enclosed by the surface z = x^2 * y * e^y - 1 is infinite.
To find the volume of the solid enclosed by the surface given by the equation z = x^2 * y * e^y - 1, we can use a triple integral over the region of interest. Since the equation does not provide any bounds or limits, let's assume we are considering the entire space.
The volume V can be calculated as:
V = ∭E dV
where E represents the region enclosed by the surface.
We'll set up the integral in Cartesian coordinates (x, y, z). The limits of integration depend on the region of interest, but since we don't have specific bounds, we'll integrate over the entire space:
V = ∫∫∫E dV
Now, we need to express the volume element dV in terms of Cartesian coordinates. In this case, dV = dx * dy * dz.
V = ∫∫∫E dx * dy * dz
Next, we'll set up the integral limits. Since we're considering the entire space, we'll integrate from negative infinity to positive infinity for each variable:
V = ∫(-∞ to ∞) ∫(-∞ to ∞) ∫(-∞ to ∞) dx * dy * dz
Now, we can evaluate the integral:
V = ∫(-∞ to ∞) ∫(-∞ to ∞) [∫(-∞ to ∞) dx] dy * dz
Since the innermost integral with respect to x is over the entire space, it evaluates to the length of the interval, which is ∞ - (-∞) = ∞.
V = ∫(-∞ to ∞) ∫(-∞ to ∞) ∞ dy * dz
Again, since the integral with respect to y is over the entire space, it evaluates to the length of the interval, which is ∞ - (-∞) = ∞.
V = ∫(-∞ to ∞) ∞ dz
Finally, we have the integral with respect to z over the entire space, which also evaluates to the length of the interval, ∞ - (-∞) = ∞.
Therefore, the volume of the solid enclosed by the surface z = x^2 * y * e^y - 1 is infinite.
Learn more about surface here:
https://brainly.com/question/29298005
#SPJ11
Find the volume of the cone. Use 3.14 for pi. Round your answer to the nearest tenths
place.

Answers
The volume of the cone is approximately 37.7 cubic units
What is volume?
A volume is simply defined as the amount of space occupied by any three-dimensional solid. These solids can be a cube, a cuboid, a cone, a cylinder, or a sphere. Different shapes have different volumes.
To find the volume of a cone, we use the formula:
V = (1/3) * π * r² * h
where π is the constant pi, r is the radius of the base of the cone, and h is the height of the cone.
Plugging in the given values, we get:
V = (1/3) * 3.14 * 3² * 4 ≈ 37.7
Therefore, the volume of the cone is approximately 37.7 cubic units (rounded to the nearest tenth).
To know more about volume visit:
https://brainly.com/question/463363
#SPJ1
Work out an expression, in terms of x, for the perimeter of the shape.
Simplify your answer.
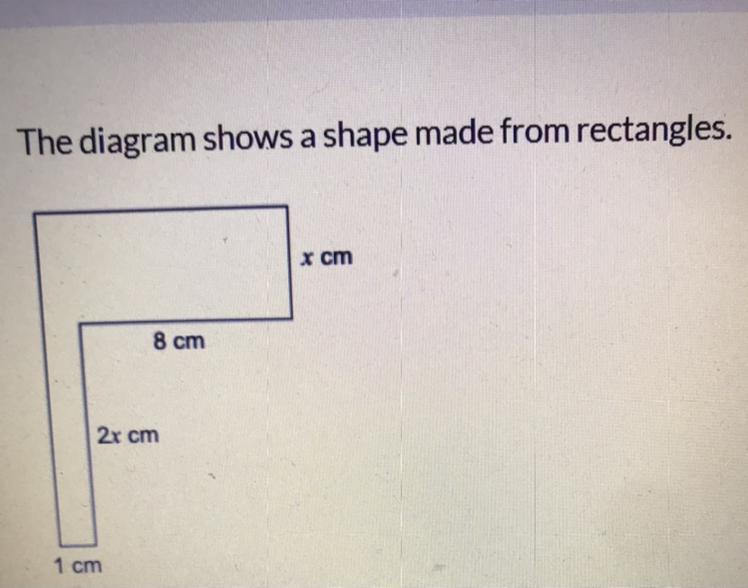
Answers
Answer:1+3x+9+x+8+2x= 6x+9
so =3(x+3)
Step-by-step explanation:
coordinate plane with quadrilaterals abcd and efgh with a at 0 comma 0, b at 2 comma 0, c at 2 comma negative 2, d at 0 comma negative 2, e at 1 comma 5, f at 7 comma 5, g at 7 comma 1, and h at 1 comma 1 are quadrilaterals abcd and efgh similar?
Answers
Quadrilaterals ABCD and EFGH are similar.To determine if quadrilaterals ABCD and EFGH are similar, we need to compare their corresponding sides and angles.
Quadrilateral ABCD has side lengths of AB = 2, BC = 2, CD = 2, and DA = 2. The lengths of its sides are equal, and its angles are all 90 degrees. Quadrilateral EFGH has side lengths of EF = 6, FG = 6, GH = 6, and HE = 6. The lengths of its sides are equal, and its angles are all 90 degrees. From the side lengths and angles, we can see that both quadrilaterals have the same shape, a rectangle. Therefore, quadrilaterals ABCD and EFGH are similar.
Similarity means that corresponding angles are equal, and corresponding sides are in proportion. In this case, both the angles and side lengths are the same for both quadrilaterals, confirming their similarity.
To learn more about quadrilaterals click here: brainly.com/question/29934291
#SPJ11
Triangle PQR is isosceles with PQ = PR. A semi-circle
with diameter [PR] is drawn which cuts [QR] at X.
Prove that X is the midpoint of [QR).
![Triangle PQR is isosceles with PQ = PR. A semi-circlewith diameter [PR] is drawn which cuts [QR] at X.Prove](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/jCyWIQMyYULjdnSZoZKbFn1thwasHnif.jpeg)
Answers
Determine the present value p you must invest to have the future value a at simple interest rate r after time t. a = $19,000, r = 11.5%, t = 4 years the present value that must be invested to get $19,000 after 4 years at an interest rate of 11.5% is $__. (round up to the nearest cent.)
Answers
The present value that must be invested to get $19,000 after 4 years at an interest rate of 11.5% is $13,013.70
What is simple interest?
The simple interest of an investment is determined as the principal investment, also known as the present value multiplied by the interest rate and the number of years, which means that the future value can be modeled as shown below:
A=PRT+P
A=P(RT+1)
A=future value=$19,000
P=present value=unknown
R=rate of return=11.5%
T=number of years that investment lasted=4
$19,000=P*(11.5%*4+1)
$19,000=P(0.46+1)
$19,000=P*1.46
P=$19000/1.46
P=$13,013.70
Find out more about simple interest on:https://brainly.com/question/25845758
#SPJ1
What do you notice about the teams’ scores?
Answers
Answer:
dont u need a picture so we can answer
Step-by-step explanation:
A high school gym class was jumping rope. They wanted to know how many jumps each student could make before they missed. The results are listed below.25679111214141517192122232427323539394447536061828588909396101103114125
Answers
As per the given data, the median number of jumps that the student made before missing is 33.5.
The term Median in math is defined as the middle value or the average of the two center values of a data set.
Here we have given that the high school gym class was jumping rope. They wanted to know how many jumps each student could make before they missed.
Here the results are listed as follows:
=> 2, 5, 6, 7, 9, 11, 12, 14, 14, 15, 17, 19, 21, 22, 23, 24, 27, 32, 35, 39, 39, 44, 47, 53, 60, 61, 82, 85, 88, 90, 93, 96, 101, 103, 114, 125
Here we need to find the center values that is written as,
=> 32, 35
Now, we have to find the average of the two center values is written as,
=> (32+35)/2 = 33.5
Then the median number of jumps is 33.5.
To know more about median here.
https://brainly.com/question/16299559
#SPJ4
Write
0.189
as a fraction in simplest form.
Answers
Answer:
Step-by-step explanation:
Rewrite the decimal number as a fraction with 1 in the denominator
\(0.189 = \frac{189}{1000}\)
Multiply to remove 3 decimal places. Here, you multiply top and bottom by = \(10^{3} = 1000\)
\(\frac{0.189}{1} * \frac{1000}{1000} = \frac{189}{1000}\)
In conclusion,
\(0.189 = \frac{189}{1000}\)
the simplest form of \(\frac{189}{1000}\) is \(\frac{189}{1000}\) because
In order to simplify a fraction there must be:
1. A number that will divide evenly into both the numerator and denominator so it can be reduced. No such number exists for 189 and 1000.
or
2. The numerator must be greater than the denominator, (an improper fraction), so it can be converted to a mixed number. 189 is not greater than 1000.
This fraction is in simplest form:
\(\frac{189}{1000}\)
Have a wonderful day
A sea lion was swimming at 5 feet below sea level. The number line shows
the location of the sea lion. It then swam down 2 feet. Describe how to use
the number line to find the new location of the sea lion.

Answers
Answer:
the answer is d.
Step-by-step explanation:
A PE X
Makayla mows two lawns the first lawn in 10 feet lawn and 7 feet wide the area of the second lawn is 7 times as big but has the same width as the first what it the length of the second lawn
Answers
The second lawn that Makayla mows has a length of 70 feet.
If the first lawn Makayla mows is 10 feet long and 7 feet wide, use the formula for the area of rectangle to know the area of the first lawn.
A = l x w
Area of first lawn = 10 feet x 7 feet
Area of first lawn = 70 ft^2
If the area of the second lawn is 7 times as big as the first, then the area of the second lawn is:
Area of second lawn = 7 x Area of first lawn
Area of second lawn = 7 x 70 ft^2
Area of second lawn = 490 ft^2
If the second lawn has the same width as the first, which is 7 feet, using the formula for the area of a rectangle, solve for the length of the second lawn.
A = l x w
Area of second lawn = l x w
490 ft^2 = l x (7 feet)
l = 70 feet
Learn more about area of rectangle here: https://brainly.com/question/25292087
#SPJ4
d/d{cosec^-1(1+x²/2x)} is equal to

Answers
Step-by-step explanation:
\(\large\underline{\sf{Solution-}}\)
\(\rm :\longmapsto\:\dfrac{d}{dx} {cosec}^{ - 1} \bigg( \dfrac{1 + {x}^{2} }{2x} \bigg)\)
Let assume that
\(\rm :\longmapsto\:y = {cosec}^{ - 1} \bigg( \dfrac{1 + {x}^{2} }{2x} \bigg)\)
We know,
\(\boxed{\tt{ {cosec}^{ - 1}x = {sin}^{ - 1}\bigg( \dfrac{1}{x} \bigg)}}\)
So, using this, we get
\(\rm :\longmapsto\:y = sin^{ - 1} \bigg( \dfrac{2x}{1 + {x}^{2} } \bigg)\)
Now, we use Method of Substitution, So we substitute
\( \red{\rm :\longmapsto\:x = tanz \: \rm\implies \:z = {tan}^{ - 1}x}\)
So, above expression can be rewritten as
\(\rm :\longmapsto\:y = sin^{ - 1} \bigg( \dfrac{2tanz}{1 + {tan}^{2} z} \bigg)\)
\(\rm :\longmapsto\:y = sin^{ - 1} \bigg( sin2z \bigg)\)
\(\rm\implies \:y = 2z\)
\(\bf\implies \:y = 2 {tan}^{ - 1}x\)
So,
\(\bf\implies \: {cosec}^{ - 1}\bigg( \dfrac{1 + {x}^{2} }{2x} \bigg) = 2 {tan}^{ - 1}x\)
Thus,
\(\rm :\longmapsto\:\dfrac{d}{dx} {cosec}^{ - 1} \bigg( \dfrac{1 + {x}^{2} }{2x} \bigg)\)
\(\rm \: = \: \dfrac{d}{dx}(2 {tan}^{ - 1}x)\)
\(\rm \: = \: 2 \: \dfrac{d}{dx}( {tan}^{ - 1}x)\)
\(\rm \: = \: 2 \times \dfrac{1}{1 + {x}^{2} } \)
\(\rm \: = \: \dfrac{2}{1 + {x}^{2} } \)
Hence,
\( \purple{\rm :\longmapsto\:\boxed{\tt{ \dfrac{d}{dx} {cosec}^{ - 1} \bigg( \dfrac{1 + {x}^{2} }{2x} \bigg) = \frac{2}{1 + {x}^{2} }}}}\)
Hence, Option (d) is correct.
The sum weights of tana and vara is 60kg and differences is 20 kg. find the weights of tana and vara.
Answers
Answer:
40kg and 20kg
Step-by-step explanation:
Answer:tana is 40 , Vara is 20
Step-by-step explanation:let x be tana, y be Vara.
x + y = 60
x - y = 20
Eliminate x by subtracting both equations.
Y -(-y) = 40
2y = 40
Y =20
Sub y=20 into x+y =60
X + 20 =60
X = 40
Use SD and determine relationship
of polynomial and linear expression.
x³ + 9x²-16x-144 (division symbol) x +9
Answers
The polynomial expression x³ + 9x² - 16x - 144 can be factored as (x + 9)(x² - x - 16) with a remainder of -288 when divided by the linear expression x + 9.
To determine the relationship between the polynomial expression x³ + 9x² - 16x - 144 and the linear expression x + 9, we can use synthetic division (SD) to divide the polynomial expression by the linear expression.
The polynomial expression can be rewritten as:
x³ + 9x² - 16x - 144 = (x + 9)(x² - x - 16)
Using synthetic division, we divide the polynomial expression by x + 9:
-9 | 1 9 -16 -144
---------------------
1 0 -16 -288
The result of the division is 1x² + 0x - 16 with a remainder of -288.
Therefore, the relationship between the polynomial expression x³ + 9x² - 16x - 144 and the linear expression x + 9 is that the polynomial expression can be factored as (x + 9)(x² - x - 16) with a remainder of -288.
This means that the polynomial expression can be written as the product of the linear expression x + 9 and the quadratic expression x² - x - 16. The remainder -288 indicates that there is no perfect division, and there is a leftover term of -288.
For more such question on polynomial. visit :
https://brainly.com/question/4142886
#SPJ8
Determine whether the numerical value is a parameter or a statistic. Explain your reasoning.
Sixty-two of the 97 passengers aboard the Hindenburg airship survived its explosion.
Answers
The numerical value "62" is a statistic because it is based on the sample of passengers aboard the Hindenburg airship.
In the given scenario, the numerical value is "62." We are told that there were 97 passengers aboard the Hindenburg airship and that 62 of them survived its explosion.
Since the numerical value is based on the sample (i.e., the passengers aboard the Hindenburg airship), it is a statistic. It describes the proportion of passengers who survived the explosion in the sample.
If we wanted to know the proportion of passengers who survived the explosion in the entire population (i.e., all passengers who have ever traveled on the Hindenburg airship), we would need to determine the parameter.
However, since we do not have data on the entire population, we cannot determine the parameter.
To know mare about statistic refer here:
https://brainly.com/question/29093686#
#SPJ11
evaluate the double integral. 6y 4x5 + 1 da, d = {(x, y) | 0 ≤ x ≤ 1, 0 ≤ y ≤ x2} d
Answers
The double integral of 6y * 4x^5 + 1 over the region D = {(x, y) | 0 ≤ x ≤ 1, 0 ≤ y ≤ x^2} is 20/3
A double integral is used to calculate the total amount of a quantity that is distributed over a two-dimensional region. In this case, the quantity being integrated is 6y*4x^5 + 1. To evaluate the integral, we need to integrate with respect to x and y.
The first step is to evaluate the inner integral with respect to y. The limits of integration for y are 0 and x^2.
∫(6y4x^5 + 1) dy from 0 to x^2 = ∫(6y4x^5) dy + ∫1 dy = [6/7y^74x^5] from 0 to x^2 + [y] from 0 to x^2 = (6/7)x^5x^2 + x^2 = (6/7)*x^7 + x^2The second step is to evaluate the outer integral with respect to x. The limits of integration for x are 0 and 1.
∫((6/7)*x^7 + x^2) dx from 0 to 1 = [x^8/7 + x^3/3] from 0 to 1 = 1/7 + 1/3 = 20/21 + 10/21 = 30/21 = 20/3Therefore, the double integral of 6y*4x^5 + 1 over the region D = {(x, y) | 0 ≤ x ≤ 1, 0 ≤ y ≤ x^2} is 20/3.
Learn more about Double Integral here:
https://brainly.com/question/19053586
#SPJ4
A manufacturer makes three models of a television set, model A, B, and C. A store sells 40% of model A sets, 40% of model B sets, and 20% of model C sets. Of model A sets, 3% have stereo sound; of model B sets, 7% have stereo sound; of model C sets, 9% have stereo sound. If a set is sold at random, find the probability that it has stereo sound.
Answers
The probability of stereo sound of a randomly selected set is 0.058 or 5.8%.
The given data is: Manufacturer makes three models of a television set: model A, B, and C.40% of Model A sets are sold.40% of Model B sets are sold. 20% of Model C sets are sold. 3% of Model A sets have stereo sound.7% of Model B sets have stereo sound. 9% of Model C sets have stereo sound.
The probability of the stereo sound of a randomly selected set is asked.
The probability of the stereo sound of a randomly selected set can be found by adding the probability of stereo sound of each model of the set sold multiplied by the probability of a set of that model being sold:
Probability of stereo sound of a randomly selected set = P(Model A) × P(Stereo Sound | Model A) + P(Model B) × P(Stereo Sound | Model B) + P(Model C) × P(Stereo Sound | Model C)
Let P(Model A) = probability of Model A being sold = 40/100 = 0.4
Let P(Stereo Sound | Model A) = probability of Stereo Sound given that Model A is sold = 3/100 = 0.03
P(Model B) = probability of Model B being sold = 40/100 = 0.4
Let P(Stereo Sound | Model B) = probability of Stereo Sound given that Model B is sold = 7/100 = 0.07
P(Model C) = probability of Model C being sold = 20/100 = 0.2
Let P(Stereo Sound | Model C) = probability of Stereo Sound given that Model C is sold = 9/100 = 0.09
Probability of stereo sound of a randomly selected set= P(Model A) × P(Stereo Sound | Model A) + P(Model B) × P(Stereo Sound | Model B) + P(Model C) × P(Stereo Sound | Model C)
= (0.4)(0.03) + (0.4)(0.07) + (0.2)(0.09)= 0.012 + 0.028 + 0.018
= 0.058
Therefore, the probability of stereo sound of a randomly selected set is 0.058 or 5.8%.
Learn more about probability visit:
brainly.com/question/31828911
#SPJ11
Solve 2x-5=7 please <3
Answers
Step-by-step explanation:
Given
2x - 5 = 7
2x = 7 + 5
2x = 12
x = 12 / 2
x = 6
Hope it will help :)❤
a) evaluate mv. (b) based on your answer to (a) how do you know the columns of m are dependent? use v to give a vector combination.
Answers
a) mv = Mv.
b) The columns of M are dependent where [v1, v2, ..., vn]T is a vector combination
a) Evaluate mv:If a matrix M is multiplied by a vector v, the result will be a linear combination of the columns of the matrix. That is, if M is an m×n matrix and v is a vector with n entries, then the product Mv is a linear combination of the columns of M with coefficients from v. Thus, mv = Mv.
b) Use v to give a vector combination.If the columns of M are linearly dependent, it implies that they are multiples of each other, i.e., one column is equal to a scalar multiple of another column, which can be written as an equation of the form, ci = aj where c and a are scalar multiples of jth and ith columns of M, respectively.
Hence, when we compute Mv, the linear combination of the columns of M will depend on the scalar multiples c and a.
For instance, let us assume that column j and i of M are linearly dependent. We have;
ci = aj or
M(:,j) = a*M(:,i)
where M(:,j) and M(:,i) represent jth and ith columns of M, respectively. Then, we can express M as;
M = [M(:,1), ..., M(:,j-1), M(:,i), M(:,j+1), ..., M(:,n)] = [M(:,1), ..., M(:,j-1), a*M(:,i), M(:,j+1), ..., M(:,n)]
Thus, we can rewrite the product Mv as;
Mv = [M(:,1), ..., M(:,j-1), a*M(:,i), M(:,j+1), ..., M(:,n)][v1, v2, ..., vn]T
where [v1, v2, ..., vn]T is a vector combination of the columns of M.
Therefore, if a linear combination of the columns of M results in the zero vector, it implies that the columns of M are dependent.
For more such questions on Vector combination.
https://brainly.com/question/30758379#
#SPJ11
pls help in geometry

Answers
Answer:
58.5; 300; 196.5
Step-by-step explanation:
Area of triangle 1 = (1/2) * 9 * 13 = 58.5 inches^2
Area of whole figure = (1/2) * (14+26) * 15 = 300 inches ^2
Area of shaded region = 300 - 58.5 - [(1/2) * 6 * 15] = 241.5 - 45 = 196.5 inches^2
Kylie went on a 300 mile trip to a soccer game. On the way back, due to road construction she had to drive 10 miles per hour slower. This made the trip take 1 hour longer. How fast did she drive to the soccer game
Answers
Answer:
Kylie drove at a speed of 60 miles per hour going to the soccer game.
Step-by-step explanation:
Let us assume that Kylie drove at speed x miles per hour going to the soccer game. On the way back, she had to drive at a speed of (x-10) miles per hour. We are given that the trip took 1 hour longer on the way back, which means that the time taken on the way back was greater than the time taken going to the soccer game. We can form an equation using the distance formula:
300/x = 300/(x-10) + 1
Simplifying this equation by cross multiplication, we get:
300(x-10) = 300x + x(x-10)
Simplifying further, we get:
300x - 3000 = 300x - 10x
Solving for x, we get:
x = 60
Therefore, Kylie drove at a speed of 60 miles per hour going to the soccer game.
1. Which of the following equations shows how substitution can be used to solve the following syster
y = 2x + 3
2x + 5y = 3
2x + 5y = 2x + 3
2x + 5(2x + 3) = 3
2(2x + 3) +5y = 3
y = 3