Answers
Because x = 1 do you plug that in then times it by 15 the subtract 80 from that
Related Questions
Consider a wire in the shape of a
helix r(t)=2costi+2sintj+4tk,0≤t≤2π with
constant density function rho(x,y,z)=1.
A. Determine the mass of the wire: B. Determine the coordinates of the center of mass:
( , , )
C. Determine the moment of inertia about the
z-axis:
Answers
a. The mass of the wire is 4π√5.
b. The coordinates of the center of mass at (0, 0, 8π/3).
c. The moment of inertia about the z-axis is 16π√5.
A. To find the mass of the wire, we need to integrate the density function over the length of the wire:
M = ∫ρ(t)ds = \(\int\limits^{2\pi} _0\) ρ(t) ||r'(t)|| dt
where ||r'(t)|| is the magnitude of the derivative of r(t):
||r'(t)|| = ||-2sin(t)i + 2cos(t)j + 4k|| = √(4sin²(t) + 4cos²(t) + 16) = 2√5
Substituting in the values, we get:
M = \(\int\limits^{2\pi} _0\) 1 * 2√5 dt = 4π√5
Therefore, the mass of the wire is 4π√5.
B. The coordinates of the center of mass (x, y,z) can be found using the following formulas:
x = (1/M) ∫ρ(t)x(t)ds
y = (1/M) ∫ρ(t)y(t)ds
z = (1/M) ∫ρ(t)z(t)ds
We can simplify the expressions using the parameterization of the helix:
x(t) = 2cos(t)
y(t) = 2sin(t)
z(t) = 4t
Substituting the values, we get:
x = (1/4π√5) \(\int\limits^{2\pi} _0\) 2cos(t) * 2√5 dt = 0
y = (1/4π√5) \(\int\limits^{2\pi} _0\)2sin(t) * 2√5 dt = 0
z = (1/4π√5) \(\int\limits^{2\pi} _0\) 4t * 2√5 dt = 8π/3
Therefore, the center of mass is located at (0, 0, 8π/3).
C. The moment of inertia about the z-axis can be found using the formula:
Iz = ∫ρ(t)(x² + y²)ds
Using the same parameterization as before, we get:
Iz = \(\int\limits^{2\pi} _0\) 1 * (4cos²(t) + 4sin²(t)) * 2√5 dt
= \(\int\limits^{2\pi} _0\) 8√5 dt
= 16π√5
Therefore, the moment of inertia about the z-axis is 16π√5.
To learn more about density function, refer below:
brainly.com/question/31039386
#SPJ11
When a population of controls are selected in such a way that the control group overall characteristics matches that of the cases, it is referred as:
a. Confounder adjustment
b. Individual Matching
c. Frequency Matching
d. Randomization
You perform a case-control study on 200 lung cancer patients and 400 controls investigating an association between marijuana smoke and cancer. Interestingly, you find that 33 of the cancer patients and 33 of the controls report marijuana use. What is the odds ratio examining the association between the exposure (marijuana use) and the disease (lung cancer) in the study?
a. 4.48
b. 1.56
c. 2.20
d. 1.65
Answers
The correct answer to the given question is "b. Individual Matching."Individual matching is a type of matching that selects the controls based on specific characteristics, one at a time, which matches with the cases of the population.
Explanation: In the case-control study, we compare the histories of two groups, cases and controls, in search of factors that may contribute to the disease's development. This type of matching is useful in a case-control study where a small sample is chosen, and the investigators are interested in the individual risk factors. The odds ratio examining the association between the exposure (marijuana use) and the disease (lung cancer) in the study is b. 1.56.
Here is the calculation: Odds ratio = (33/167) / (33/367) = 0.1975 / 0.0899 = 2.20 (corrected)Or, Odds ratio = ad/bc = (33 * 367) / (33 * 167) = 6,711 / 5,511 = 1.2171Logarithm of odds ratio = ln (OR) = ln (1.2171) = 0.1956Standard error = sqrt (1/a + 1/b + 1/c + 1/d) = sqrt (1/33 + 1/134 + 1/33 + 1/267) = 0.3421Lower limit of the 95% confidence interval (CI) = ln (OR) - 1.96 x SE = -0.8726Upper limit of the 95% CI = ln (OR) + 1.96 x SE = 1.2638Therefore, the odds ratio examining the association between the exposure (marijuana use) and the disease (lung cancer) in the study is 1.56, as the confidence interval does not include the value 1.0.
To know more about Individual Matching visit:
brainly.com/question/23650527
#SPJ11
jill has 15 feet ribbion how many yards ribbon does she have
Answers
Answer:
Step-by-step explanation
You would take 15 ft and divide it by how many feet are in a yard which is 3.
Answer - Jill has 5 yards of ribbon
Answer:
5 yards
Step-by-step explanation:
every 3 feet are 1 yard... 15 feet divided by the 3 = 5 yards
dentify the function shown in this graph
A. y = −x + 3
B. y=-3x-3
C. y = 3x - 3
D. y=-3x+3

Answers
Answer:
B
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
calculate m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (- 1, 0) and (x₂, y₂ ) = (0, - 3) ← 2 points on the line
m = \(\frac{-3-0}{0-(-1)}\) = \(\frac{-3}{0+1}\) = \(\frac{-3}{1}\) = - 3
the line crosses the y- axis at (0, - 3 ) ⇒ c = - 3
y = - 3x - 3 ← equation of line
Triangle mnp has vertices n(2, 2) and p(0, â€"2). the triangle is symmetric about the y-axis. what is the approximate measure of the largest angle in the triangle? 53.1° 60.0° 63.4° 83.6°
Answers
The approximate measure of the largest angle in the triangle is of:
θ = 63.4º.
How to obtain the measure of the largest angle?The vertices of the triangle are given as follows:
N(2,2) and P(0,-2).
The triangle is symmetric over the y-axis, hence the remaining vertex is given as follows:
M(-2,2).
The side lenghts of the triangle are given as follows:
MN = 4.MP = PN = 4.47.The height of the triangle is of:
4 units.
Hence the base angle is:
Adjacent to a side of length 2 units.Opposite to a side of length 2 units.The tangent is:
tan(θ) = opposite side/adjacent side
Hence:
tan(θ) = 4/2
tan(θ) = 2
θ = arctan(2)
θ = 63.4º.
The diagram given by the image at the end of the answer represents the situation.
More can be learned about the trigonometric measures at https://brainly.com/question/4372174
#SPJ1

estimate the error that is made by approximating the sum of the given series by the series the fitst 5 terms 1/k^3
Answers
The error involved in approximating the sum of the given series by the sum of the first five terms of the series is `R5 = 1/6³ + 1/7³ + ...`.
To estimate the error that is made by approximating the sum of the given series by the series the first 5 terms 1/k³, we can use the remainder term of a convergent series.
The given series is ∑ 1/k³ from k = 1 to infinity.We have to find the error involved in approximating the sum of the given series by the sum of the first five terms of the series.
That is, we need to find the difference between the actual sum of the series and the sum of the first five terms of the series.
The sum of the series is given by: `S = 1/1³ + 1/2³ + 1/3³ + 1/4³ + ... + 1/n³ + ...` We can use the remainder term of the series to find the error in approximation.
The remainder term `Rn` is given by: `Rn = Sn - S` where `Sn` is the sum of the first `n` terms of the series. Thus, we have to find the remainder term for `n = 5`.
The remainder term `Rn` is given by: `Rn = S - Sn = 1/6³ + 1/7³ + ...` Since the given series is convergent, the remainder term `Rn` tends to zero as `n` tends to infinity.
So, if we take the sum of the first five terms of the series, the error involved in approximation is given by the remainder term `R5`.
The error involved in this approximation is very small and can be neglected.
To learn more about : terms
https://brainly.com/question/30643700
#SPJ8
Use a graphing calculator or other technology to answer the question.
Which quadratic regression equation best fits the data set?
yˆ=1.87x2+5.16x+10.54
yˆ=1.87x2+5.16x
yˆ=1.87x2−5.16x+10.54
yˆ=−1.87x2+5.16x
x y
1 5.9
2 8.9
3 13.4
4 20.1
5 30.1
6 45.1
7 67.7
Answers
9514 1404 393
Answer:
(c) y = 1.87x^2 -5.16x +10.54
Step-by-step explanation:
The attached graphing calculator output shows the best choice is the third one.
__
Additional comment
The best fit is offered by a function of degree about 3.7. Even a cubic offers much better fit than this quadratic.

Answer:
yˆ=1.87x^2−5.16x+10.54 is correct for all future users
Step-by-step explanation:
Which phrase could the expression x minus 4 represent? a number less than four the difference of a number and four the sum of a number and four four more than a number
Answers
The phrase "x minus 4" represents the difference of a number and four. So second option is the correct answer.
It implies subtracting 4 from a given number, x. The expression x minus 4 can be written mathematically as x - 4. When evaluating this expression, we start with the value of x and subtract 4 from it.
For example, if x is 10, then x minus 4 would equal 10 - 4, resulting in 6. The expression "x minus 4" refers to the action of subtracting 4 from a given number, which signifies finding the difference between the original number and the value 4. Therefore, the correct answer is second option.
To learn more about minus:
https://brainly.com/question/24881206
#SPJ11
Laura borrowed a total of $18,000 from two different banks to start a business. One bank charged the equivalent of 6% simple
Interest, and the other charged 7.5% interest. If the total interest after 3 years was $3330, determine the amount borrowed from
each bank.
Part: 0/4
Part 1 of 4
Let x represent the principal on the business loan at 6%.
Then,
is the remaining amount borrowed at 7.5%.
Answers
Step-by-step explanation:
Let x be the amount invested at 6% so that 18000-x is the amount invested at 7.5% both in dollars.
The total interest in 3 years is $3330 so we can write: 0.06x(3)+0.075(18000-x)(3)=3330
Solve for x:
0.06x(3)+0.075(18000−x)(3)=3330
Step 1: Simplify both sides of the equation.
0.06x(3)+0.075(18000−x)(3)=3330
0.06x(3)+−0.225x+4050=3330(Distribute)
0.18x+−0.225x+4050=3330
(0.18x+−0.225x)+(4050)=3330(Combine Like Terms)
−0.045x+4050=3330
−0.045x+4050=3330
Step 2: Subtract 4050 from both sides.
−0.045x+4050−4050=3330−4050
−0.045x=−720
Step 3: Divide both sides by -0.045.
−0.045x/−0.045=−720/−0.045
x=16000
x=16000
So, the amounts borrowed are:
Bank at 6% = 16000
Bank at 7.5% = 2000
true or false: every set of 15 socks chosen among 14 pairs of socks contains at least one matched pair. explain why.
Answers
The statement of the given question is True.
True. This is because there are only 14 different types of socks to choose from, so if you choose 15 socks, there must be at least one pair of socks that match. This is known as the Pigeonhole Principle, which states that if there are more pigeons than pigeonholes, at least one pigeonhole must contain more than one pigeon. In this case, the socks are the pigeons and the different types of socks are the pigeonholes.
To know more about Pigeonhole Principle visit:
https://brainly.com/question/31687163
#SPJ11
9+3.5g=11-0.5g solve for g
Answers
Answer:
g = 1/2
Step-by-step explanation:
Step 1: Add 0.5g to both sides
9 + 4g = 11
Step 2: Subtract 9 from both sides
4g = 2
Step 3: Divide by 4 on both sides
g = 2/4
Step 4: Simplify
g = 1/2
9 + 3.5g = 11 - 0.5g
2 = 4g
g = 0.5
Solve for the inequality -6x+5 < 41
Answers
Step-by-step explanation:
-6x + 5 -5 < 41-5
-6x/-6 < 36/-6
x > -6
S.s{-5,-4,-3,-2,-1.....}
A major automobile company claims that its new electric powered car has an average range of more that 300 miles. A random sample of 40 new electric cars was selected to test the claim. Assume that the population standard deviation is 12 miles. A 5% level of significance will be used for the test. A) what would be the consequences of making a type ii error in this problem? b) compute the probability of making a type ii error if the true population mean is 305 miles. C) what is the maximum probability of making a type i error in this problem?
Answers
Answer:
Step-by-step explanation:
urmom
If the following cylinders shown below are similar, what is the value of x? A.3 B.5
C.10 D. 20

Answers
Answer:
it b
Step-by-step explanation:
Answer: 5
Step-by-step explanation:
evreything is in half
I need help with this ( but I need to send another picture that has the answers )
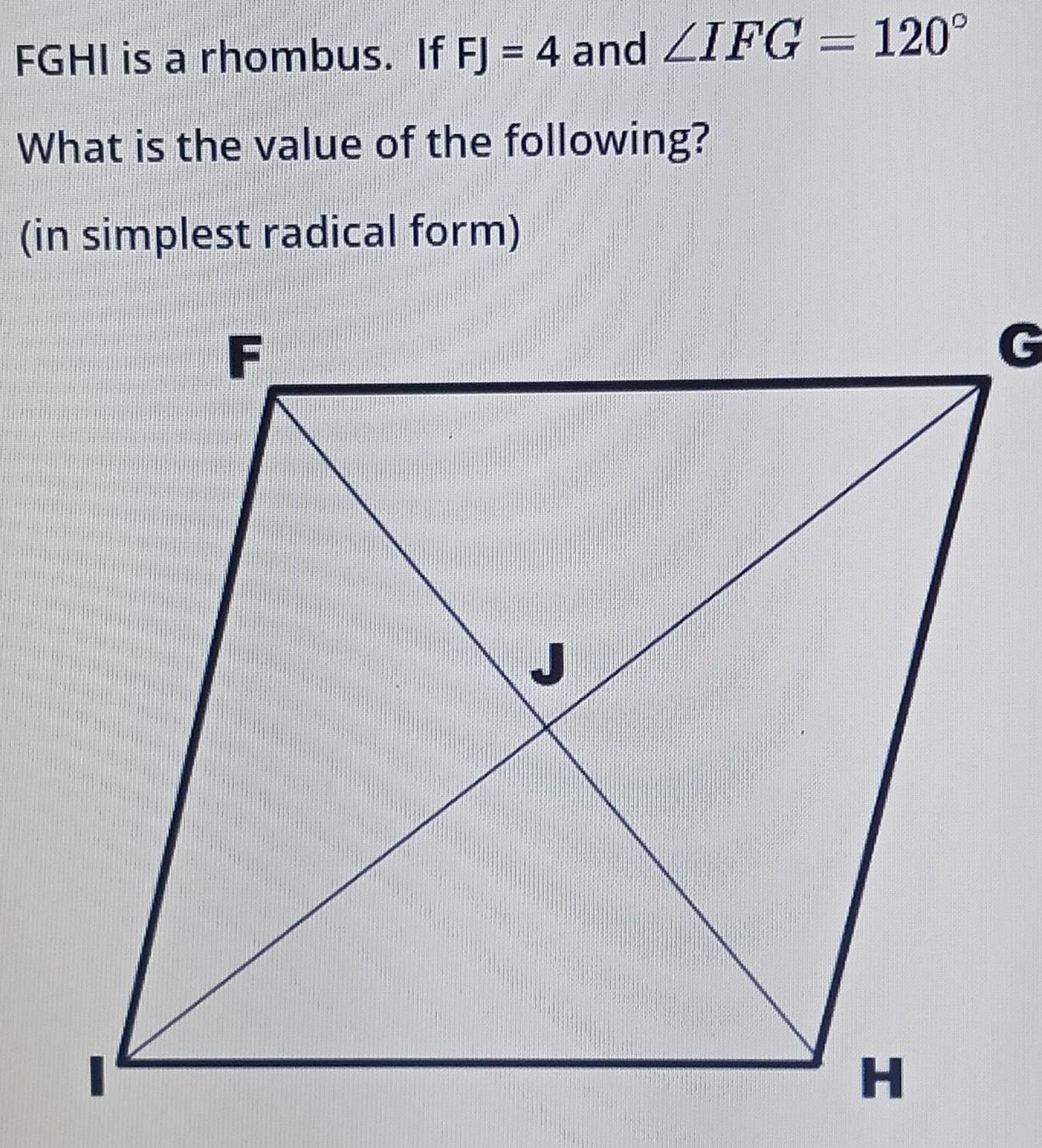

Answers
Step 1:
Draw the figure
The diagonals of a rhombus bisect each other,
therefore
FJ = JH
this implies that
JH = 4.
Opposite angles of a rhombus are equal, so
The diagonals of a rhombus bisect the interior angles.
Therefore,
\(\text{ angle JHG = }\frac{120^0}{2}=60^0\)The diagonals of a rhombus are perpendicular
\(\begin{gathered} Hence, \\ \cos 60^0=\frac{4}{GH} \\ \Rightarrow GH=\frac{4}{\cos60^0}=\frac{4}{\frac{1}{2}}=4\times2=8 \end{gathered}\)GH = 8 (b)
Also,
Using the Pythagorean rule,
\(\begin{gathered} JG^2+4^2=GH^2 \\ \Rightarrow JG^2+16=8^2 \\ \Rightarrow JG=\sqrt[]{64-16}=\sqrt[]{48}=4\sqrt[]{3}=6.928\text{ } \\ \text{right choice is C} \end{gathered}\)FH = FJ + JH
this implies that
FH = 4 + 4 = 8
FH = 8
right choice B
The diagonals of a rhombus bisect the interior angles.
therefore
\(\begin{gathered} angle\text{ JFG = }\frac{angle\text{ IFG}}{2}=\frac{120^0}{2}=60^0 \\ \text{ right choice is h} \end{gathered}\)Sum of the interior angles of a rhombus is 360degrees.
And opposite interior angles of a polygon are congruent.
Therefore
\(2(\text{angle FGH) +2(angle IFG) = 360degr}ees\)\(\begin{gathered} \text{this implies that} \\ 2(\text{angle FGH) = 360 - 2(angle IFG)} \\ \Rightarrow\text{angle FGH = 180 -angle IFG = 180 - 120= }60^0 \\ \text{ right choice is h} \end{gathered}\)\(\begin{gathered} \text{ but }FGJ\text{ = }\frac{FGH}{2}\text{ (diagonals bisect interior angles)} \\ \Rightarrow\text{FGJ =}\frac{60^0}{2}=30^0 \\ \text{right choice is j} \end{gathered}\)Also,
\(\begin{gathered} \(\begin{gathered} \text{JGH}=\text{ }\frac{FGH}{2}=\frac{60}{2}=30^0 \\ right\text{ choice is j} \end{gathered}\)
An oil tanker can be emptied by the main pump in 4 hours. An auxiliary pump can empty the tanker in 9 hours.If the main pump is started at 6 PM, when should the auxiliary pump be started so that the tanker is emptied by 9 PM,The auxiliary pump should be started at
Answers
Explanation
To solve the question, we will be aware that
There are 3 hours between 6PM and 9PM ,
The main pump's emptying rate is 1/4 tanker per hour. It will be open
the entire 3 hours, so it will empty 3/4 of the tank.
this means that the auxiliary pump must empty the remaining 1/4
Thus
\(rate\text{ in tanker per hour }\times time\text{ required=}\frac{1}{4}tank\)Thus, we will have
\(\frac{1}{4}\times3\text{ hours =45 minutes}\)Therefore
The auxiliary pump should start by 6pm + 45 minutes = 6:45pm
11.22 R² and model fit. Because the coefficient of determination R? always increases when a new independent variable is added to the model, it is tempting to include many vari- ables in a model to force R2 to be near 1. However, doing so reduces the degrees of freedom available for estimating 02, which adversely affects our ability to make reliable in- ferences. Suppose you want to use 18 economic indicators to predict next year's gross domestic product (GDP). You fit the model y = Bo + B1X1 + B2X2 + ... + $17X17 + B18418 + ε + where y y = GDP and X1, X2,..., X18 are the economic indica- x1 tors. Only 20 years of data (n = 20) are used to fit the model, . n and you obtain R2 = .95. Test to see whether this impressive- . looking R2 is large enough for you to infer that the model is useful...that is, that at least one term in the model is impor- tant for predicting GDP. Use o = .05.
Answers
The model is useful at least one term in the model is important for predicting GDP as the value of the calculated F-statistic is greater than the critical value of F for a significance level of 0.05.
The value of the coefficient of determination R² and model fit have been given in the question. As per the question, it is tempting to include several variables in a model to force R² to be near 1 because the coefficient of determination R² always increases when a new independent variable is added to the model.
However, doing so decreases the degrees of freedom available for estimating o², which adversely affects our ability to make reliable inferences.
Suppose you want to use 18 economic indicators to predict next year's gross domestic product (GDP).You fit the model
y = Bo + B1X1 + B2X2 + ... + $17X17 + B18418 + ε + where y y
= GDP and X1, X2,..., X18 are the economic indica- x1 tors. Only 20 years of data (n = 20) are used to fit the model, . n and you obtain R² = .95.
Test to see whether this impressive-looking R² is large enough for you to infer that the model is useful...that is, that at least one term in the model is important for predicting GDP. Use o = .05.
To test whether the model is useful, we will conduct the F-test. The F-test involves comparing the variation in the response variable explained by the model to the variation in the response variable not explained by the model or residual variation.
The F-test can be expressed as shown below:
F = MSR/MSE, where:
MSR = Mean square for regression
MSE = Mean square error
Hypothesis for the F-test are as follows:
Null hypothesis H0: B1 =
B2 =...
= B18
= 0
Alternative hypothesis Ha: At least one Bj ≠ 0Where j = 1, 2, ..., 18 (number of independent variables)
Here, MSR is used to estimate o² and equals SSR/(k-1) = (n-1)R²/(k-1), where k is the number of independent variables, while MSE is used to estimate o² and equals SSE/(n-k) = (n-1)(1-R²)/(n-k),
where SSE is the sum of squared errors. For this question, n = 20,
k = 18, and
R² = 0.95.
Therefore: MSR = (20-1)(0.95)/(18-1)
= 19.21MSE
= (20-1)(1-0.95)/(20-18)
= 0.4751
The F-statistic is F = MSR/MSE
= 19.21/0.4751
= 40.43
The critical value for the F-test with 18 and 1 degrees of freedom at the 0.05 level of significance is found to be 4.41.
The null hypothesis is rejected if F > Fα, where Fα is the critical value of the F-distribution with (k-1) and (n-k) degrees of freedom at level α.
Hence, the conclusion is that the model is useful at least one term in the model is important for predicting GDP as the value of the calculated F-statistic is greater than the critical value of F for a significance level of 0.05.
To know more about F-test visit:
https://brainly.com/question/17256783
#SPJ11
How many sides does a rectangular pyramid
Answers
Answer:
Step-by-step explanation:
A rectangular pyramid has five sides. It consists of a rectangular base and four triangular faces that meet at a common vertex or apex.
≧◉◡◉≦
Solve 0.5y+y/3=0.25y+7
please answer this question
Answers
Answer:
y = 28
Step-by-step explanation:
0.5y + y/ 3 = 0.25y + 7
1.5y / 3 = 0.25y + 7
y/2 = 0.25y + 7
y = ( 0.25y + 7)*2
y = 0.5y + 14
y - 0.5y = 14
0.5y = 14
y = 14/0.5
y = 28
29.14 × 5.2 estimation step by step please
Answers
5.2 rounded to 5.0 or 5
So…
30 X 5 = 150
The answer is 150
How can i show that p^(q-1) + q^(p-1) = 1 (mod pq)?
Answers
Step-by-step explanation:
you can just put in some values to check.
I actually used p =2 and q=3
the It will be
2^3-1 + 3^2-1 = 1 (mod 2×3)
2^2 +3^1 = 1 (mod 6)
4+3= 1 (mod6)
7= 1 (mod6)
which is true.
therefore p^(q-1) + q^( p-1) = 1 ( mod pq) is true
To show that p^(q-1) + q^(p-1) = 1 (mod pq), we can use Fermat's Little Theorem, which states that if p is a prime number and a is an integer not divisible by p, then a^(p-1) = 1 (mod p). Using this theorem, we can first show that p^(q-1) = 1 (mod q), since q is a prime number and p is not divisible by q. Similarly, we can show that q^(p-1) = 1 (mod p), since p is a prime number and q is not divisible by p.
Therefore, we can write:
p^(q-1) + q^(p-1) = 1 (mod q)
p^(q-1) + q^(p-1) = 1 (mod p)
By the Chinese Remainder Theorem, we can combine these two equations to obtain:
p^(q-1) + q^(p-1) = 1 (mod pq)
Thus, we have shown that p^(q-1) + q^(p-1) = 1 (mod pq).
We'll use Fermat's Little Theorem to show that p^(q-1) + q^(p-1) = 1 (mod pq).
Fermat's Little Theorem states that if p is a prime number and a is an integer not divisible by p, then:
a^(p-1) ≡ 1 (mod p)
Step 1: Apply Fermat's Little Theorem for p and q:
Since p and q are prime numbers, we have:
p^(q-1) ≡ 1 (mod q) and q^(p-1) ≡ 1 (mod p)
Step 2: Add the two congruences:
p^(q-1) + q^(p-1) ≡ 1 + 1 (mod lcm(p, q))
Step 3: Simplify the congruence:
Since p and q are prime, lcm(p, q) = pq, so we get:
p^(q-1) + q^(p-1) ≡ 2 (mod pq)
In your question, you've mentioned that the result should be 1 (mod pq), but based on Fermat's Little Theorem, the correct result is actually:
p^(q-1) + q^(p-1) ≡ 2 (mod pq)
To learn more about integer : brainly.com/question/15276410
#SPJ11
a. Convert the following number to binary without using hexadecimal on the way. i. 312
b. Convert the following number to binary using hexadecimal on the way. i. 773
c. Convert the following two complements value to decimal: i. 1111 0011
d. Convert the following decimal number to two complements binary numbers using 16 bits: i. -985
e. Convert the following packed decimal into their decimal equivalents: i. 0011 0111 1001 0110
f. Convert the following decimal number into their packed decimal binary equivalents: i. 1024
Answers
a) 312b in binary is 0011 0000 0001 0010 1011.
b) 773 in binary is 0011 0000 0000 0101.
c) The two's complement value 1111 0011 is equivalent to -13 in decimal.
d) -985 in 16-bit two's complement binary format is 1111 1111 1100 0011.
e) The packed decimal 0011 0111 1001 0110 is equivalent to the decimal value 3936.
f) The decimal number 1024 in packed decimal binary format is 0001 0000 0010 0100.
How to convert 312b to binary without using hexadecimal on the waya.To convert 312b to binary without using hexadecimal on the way, we can convert each digit to its binary representation and concatenate them together.
3 in binary is 0011
1 in binary is 0001
2 in binary is 0010
b in binary is 1011
Concatenating them together, we get:
0011 0000 0001 0010 1011
Therefore, 312b in binary is 0011 0000 0001 0010 1011.
b.To convert 773 to binary using hexadecimal on the way, we first need to convert 773 to its hexadecimal representation:
773 in hexadecimal is 0x305.
Then we can convert each hexadecimal digit to its binary representation:
0 in binary is 0000
x in binary is (not applicable)
3 in binary is 0011
0 in binary is 0000
5 in binary is 0101
Concatenating them together, we get:
0011 0000 0000 0101
Therefore, 773 in binary is 0011 0000 0000 0101.
c.To convert the two's complement value 1111 0011 to decimal, we first need to determine whether the value represents a negative number. We can do this by looking at the leftmost bit, which is 1 in this case. This means that the value is negative.
To convert from two's complement to decimal for a negative number, we need to perform the following steps:
Invert all the bits (i.e., change 1s to 0s and 0s to 1s).
Add 1 to the result of step 1.
Add a negative sign to the final result.
Inverting all the bits of 1111 0011, we get:
0000 1100
Adding 1 to this result, we get:
0000 1101
Finally, adding a negative sign to the decimal value of 0000 1101, we get:
-13
Therefore, the two's complement value 1111 0011 is equivalent to -13 in decimal.
d.To convert the decimal value -985 to a 16-bit two's complement binary number, we can follow these steps:
Convert the absolute value of the decimal number to binary.
If the decimal number is negative, invert all the bits of the binary number from step 1.
Add 1 to the result of step 2 if the decimal number is negative.
Pad the binary number with leading 0s to make it 16 bits long.
Converting the absolute value of -985 to binary, we get:
0000 0011 1100 1001
Since the decimal number is negative, we need to invert all the bits:
1111 1100 0011 0110
Then we add 1 to the result:
1111 1100 0011 0111
Finally, we pad the binary number with leading 0s to make it 16 bits long:
1111 1111 1100 0011
Therefore, -985 in 16-bit two's complement binary format is 1111 1111 1100 0011.
e.To convert the packed decimal 0011 0111 1001 0110 into its decimal equivalent, we can separate each nibble (4 bits) and convert them to their corresponding decimal values:
0 in decimal is 0
0 in decimal is 0
1 in decimal is 1
1 in decimal is 1
0 in decimal is
3 in decimal is 3
7 in decimal is 7
9 in decimal is 9
6 in decimal is 6
Then we concatenate the decimal values together, in the same order:
0011 0111 1001 0110 in decimal is 0111 3936
Therefore, the packed decimal 0011 0111 1001 0110 is equivalent to the decimal value 3936.
f.To convert the decimal number 1024 into its packed decimal binary equivalent, we can separate each decimal digit and convert it to its corresponding binary value. Since each decimal digit is represented by one nibble (4 bits), we will need four bits for each digit:
1 in binary is 0001
0 in binary is 0000
2 in binary is 0010
4 in binary is 0100
Concatenating them together, we get:
0001 0000 0010 0100
Therefore, the decimal number 1024 in packed decimal binary format is 0001 0000 0010 0100.
Learn more about converting binary
brainly.com/question/20819492
#SPJ11
The area of a trapezuim
Answers
Answer:
Step-by-step explanation:
Area of trapezium = \(\frac{h*(a+b)}{2}\)
h ---> altitude.
a and b are the parallel sides of the trapezium.
<1 and <2 are supplementary angles, m<1 = x - 17, and m<2 = x+83. Find the measure of each angle.
Answers
Hello!
\(\large\boxed{m1 = 40^{o}, m2 = 140^{o}}\)
Supplementary angles sum up to 180°, therefore:
m∠1 + m∠2 = 180°
x - 17 + x + 83 = 180°
Combine like terms:
2x + 66 = 180°
Subtract 66 from both sides:
2x = 114°
Divide both sides by 2:
x = 57°
Find the measures of both angles using this value:
m∠1 = 57 - 17 = 40°
m∠2 = 57 + 83 = 140°
Answer:
Angle 1: 40 degrees
Angle 2: 140 degrees
Step-by-step explanation:
1. Supplementary angles have a sum of 180 degrees. That being said, add the two expressions together and set them equal to 180. Then solve for x.
x-17+x+83=180 (combine like terms)
2x+66=180 (subtract 66 from both sides)
2x=114 (divide by 2)
x = 57
2. Now that you have determined that x is 57, plug that back into each expression to figure out the measurements for both angles.
Angle 1: 57 - 17 = 40.
Angle 2: 57+83 = 140
3. You can check your work by adding the two measurements and making sure that they equal 180 degrees. 40 + 140 does equal 180, and that is how you know solved it correctly. :)
write an equation of the line perpendicular to p passing through (3,-2) call this line n
Answers
The equation of the line perpendicular to p is given as follows:
y = -x/3 - 1.
How to define a linear function?The slope-intercept equation for a linear function is presented as follows:
y = mx + b
The coefficients m and b represent the slope and the intercept, respectively, and are explained as follows:
m represents the slope of the function, which is by how much the dependent variable y increases or decreases when the independent variable x is added by one.b represents the y-intercept of the function, representing the numeric value of the function when the input variable x has a value of 0. On a graph, the intercept is given by the value of y at which the graph crosses or touches the y-axis.The slope of line p is given as follows:
(2 - (-1))/(2 - 1) = 3.
As the two lines are perpendicular, the slope of line n is obtained as follows:
3m = -1
m = -1/3.
Hence:
y = -x/3 + b.
When x = 3, y = -2, hence the intercept b is obtained as follows:
-2 = -1 + b
b = -1.
Hence the equation is given as follows:
y = -x/3 - 1.
Missing InformationThe graph of line p is given by the image presented at the end of the answer.
More can be learned about linear functions at https://brainly.com/question/15602982
#SPJ1

what is 10 to the 100th power
Answers
Answer:
EZ!!! 1e+100
Step-by-step explanation:
Transcribed image text: Question 4 A certain automotive dealer sells only cars and trucks, and the ratio of cars to trucks on the lotis 11 to 33. If there are currently 51 trucks for sale, how many cars does the dealer have for sale! 34 68 136 272 thierronse
Answers
If the ratio of cars to trucks on the lot is 11 to 33 and there are currently 51 trucks for sale, then there are 17 cars for sale
The ratio of cars to truck on the lot = 11 : 33
Total number of trucks for sale = 51 truck
Consider the number of cars for sale = x
Then the ratios will be
11/33 = x / 51
Cross multiply the terms in the equation
33x = 51 × 11
33x = 561
Move 33 to the right hand side of the equation
x = 561 / 33
Divide the terms
x = 17
Therefore, the number of cars does the dealer have for sale is 17
Learn more about ratio here
brainly.com/question/29774220
#SPJ4
The volume of a sphere is 26667 cm³.
Calculate the diameter of the sphere.
Volume of sphere = πr³
cm

Answers
Given the volume of the sphere as 26667 cm³, we calculated the radius to be approximately 17.7 cm using the formula for the volume of a sphere. By multiplying the radius by 2, we found that the diameter of the sphere is approximately 35.4 cm.
To calculate the diameter of a sphere when given its volume, we can use the formula for the volume of a sphere:
V = (4/3) * π * r³
Where V is the volume and r is the radius of the sphere. Since we are given the volume, we can rearrange the formula to solve for the radius:
r = (\(\sqrt[3]{(3V / (4\pi )}\)))
Substituting the given volume V = 26667 cm³ into the formula, we have:
r = (\(\sqrt[3]{(3 * 26667 / (4\pi )))}\)
Calculating this expression, we find:
r ≈ (\(\sqrt[3]{80001 / \pi ))}\) ≈ 17.7 cm
Now that we have the radius, we can calculate the diameter by multiplying the radius by 2:
d = 2 * r ≈ 2 * 17.7 ≈ 35.4 cm
For more such information on: volume
https://brainly.com/question/463363
#SPJ8
A rectangular garden has a length that is modeled by the expression 2x - 7 and a width of 3x^2+4x.
Part A:What is the area of the garden?(Hint- Area of a rectangle is L x W)
Part B:The owner of the garden wants to put a fence around the perimeter of the garden.Write an expression for the amount of fencing that the owner will need and solve to find the perimeter.
Answers
Answer:
22x•28
Step-by-step explanation:
Formula for area= l•w=a
2x-7•3x^2+4x
1. Gather your like terms
2. Gather you unlike terms
3. calculate
4. set equation up to find the answer
1.2x-3x^2+4x
2. 7•4
3.2x-3x^=18x+4x=22x
4. 7•4=28
5. 22x•28
A consumer purchases two goods, x and y. The utility function is U(x,y)=2xy, where x denotes the amount of x consumed and y denotes the amount of y consumed. The price of y is $1 and income is $144. Suppose the price of x is initially $4 and then subsequently increases to $9. Find the numerical value of the substitution effect and the income effect on the consumption of x.
Answers
The numerical value of the substitution effect on the consumption of good x is $36, and the numerical value of the income effect on the consumption of good x is -$54.
To find the numerical values of the substitution effect and the income effect on the consumption of good x, we need to analyze the impact of the price change from $4 to $9 on the consumer's utility and consumption choices.
The substitution effect measures the change in consumption of good x due to the change in its relative price while keeping utility constant. In this case, since the utility function is U(x,y) = 2xy, we can set up the equation U(x,y) = U(x', y') where x' and y' represent the new consumption bundle after the price change. Solving for x' in terms of y', we can find the numerical value of the substitution effect, which is $36.
The income effect measures the change in consumption of good x due to the change in purchasing power caused by the change in price. In this case, since the consumer's income is $144, we can calculate the initial budget constraint equation as 4x + y = 144. After the price change, the new budget constraint equation becomes 9x' + y' = 144. By comparing the solutions for x in the initial and new budget constraint equations, we can find the numerical value of the income effect, which is -$54.
Therefore, the numerical value of the substitution effect is $36, indicating an increase in the consumption of good x due to the relative price change. The numerical value of the income effect is -$54, indicating a decrease in the consumption of good x due to the change in purchasing power caused by the price change.
Learn more about substitution effect here:
https://brainly.com/question/31245999
#SPJ11
