If a truck hauls 5 loads per week how many loads would it haul in a year period
Answers
Answer:
73
Step-by-step explanation:
you have to divide the year period number (365) by 5.
365÷5=73
Related Questions
ASAP!!! Answer the following include all steps

Answers
Question 1:
(a) The equation representing Elaine's total parking cost is:
C = x * t
(b) So the cost of parking for a full 24 hours would be 24 times the cost per hour.
Question 2:
The given system of equations is inconsistent and has no solution.
(a) To represent Elaine's total parking cost, C, in dollars for t hours, we need to know the cost per hour. Let's assume the cost per hour is $x.
(b) If Elaine wants to park her car for a full 24 hours, we can substitute t = 24 into the equation from part (a):
C = x * 24
Question 2:
To solve the linear system:
-x - 6y = 5
x + y = 10
We can use the elimination method.
Multiply the second equation by -1 to create opposites of the x terms:
-x - 6y = 5
-x - y = -10
Add the two equations together to eliminate the x term:
(-x - 6y) + (-x - y) = 5 + (-10)
-2x - 7y = -5
Now we have a new equation:
-2x - 7y = -5
To check the answer, we can substitute the values of x and y back into the original equations:
From the second equation:
x + y = 10
Substituting y = 3 into the equation:
x + 3 = 10
x = 10 - 3
x = 7
Checking the first equation:
-x - 6y = 5
Substituting x = 7 and y = 3:
-(7) - 6(3) = 5
-7 - 18 = 5
-25 = 5
For more such questions on parking cost
https://brainly.com/question/18091509
#SPJ8
Find the length of AB when A(-4,1) and B(3,-1). Round to the nearest tenth (one decimal place) if necessary.
Answers
Answer:
7.3 units is the answer rounded
When A(-4,1) and B(3,-1), the length of AB is approximately 7.3 units.
What is distance formula?The distance formula is a mathematical formula that is used to compute the distance between two points in a coordinate plane.
This formula is derived from the Pythagorean theorem, which states that the square of the length of the hypotenuse in a right triangle equals the sum of the squares of the lengths of the other two sides.
We can use the distance formula to find the length of AB:
\(d = \sqrt{ ((x2 - x1)^2 + (y2 - y1)^2)}\)
Where (x1, y1) = (-4, 1) and (x2, y2) = (3, -1)
d = sqrt(\((3 - (-4))^2 + (-1 - 1)^2\))
= sqrt(\(7^2 + (-2)^2\))
= sqrt(49 + 4)
= sqrt(53)
≈ 7.3 (rounded to one decimal place)
Therefore, the length of AB is approximately 7.3 units.
For more details regarding distance formula, visit:
https://brainly.com/question/25841655
#SPJ2
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
Solve the simultaneous equations
2x + 5y + 11 = 0
3x - y-8= 0
Answers
Answer:
x = 1\(\frac{12}{17}\), y = -2\(\frac{15}{17}\)
Step-by-step explanation:
2x + 5y + 11 = 0 --- Equation 1
3x - y - 8 = 0
15x - 5y - 40 = 0 --- Equation 2
Equations 1+2: 2x + 5y + 11 + 15x - 5y - 40 = 0 + 0
17x - 29 = 0
17x = 29
x = 29 ÷ 17
x = 1\(\frac{12}{17}\)
Substitute x = 1\(\frac{12}{17}\) into Equation 1:
2x + 5y + 11 = 0
2(1\(\frac{12}{17}\)) + 5y + 11 = 0
3\(\frac{7}{17}\) + 5y = -11
5y = -11 - 3\(\frac{7}{17}\)
= -14\(\frac{7}{17}\)
y = -14\(\frac{7}{17}\) ÷ 5
y = -2\(\frac{15}{17}\)
Subtract:
(3x^3– 10x^2+ 13x) – (5x^3+ 4x² – 9x)
A. 8x^3 + 14x^2 - 22x
B. 8x^3 - 6x^2 + 4x
C. 2x^3 - 6x^2 - 4x
D. -2x^3 - 14x^2 + 22x
Answers
Answer:
D. -2x^3 - 14x^2 + 22x
Step-by-step explanation:
1) Remove parentheses.
3x³ - 10x² + 13x - 5x³ - 4x² + 9x
2) Collect like terms.
(3x³ - 5x³) + (-10x² - 4x²) + (13x + 9x)
3) Simplify.
-2x³ - 14x² + 22x
PLEASE HELP ON QUESTION ASAP !
hi ! I really need help understanding paragraph and I've also added a question about paragraph by me down below . Would like explanation in simple words.
If answers correct I'll rate you five stars a thanks and maybe even brainliest
Paragraph I needed help understanding:
If two or more cells are connected together side by side, the voltage across them is sum of the voltage of each cell. This is because both cells are pushing same way.
My Question about paragraph:
If the sum lets say was 4.5v would every individual cell be worth 4.5 as it says in question ' voltage across them is the sum of voltage of each cell ' or are they each a different value? And how would we be able to find value?.
Answers
If the sum of the voltage is 4.5V, it is possible that different cells have different voltages. For example, three cells with voltages 1V, 1.5V, and 2V could be connected together side by side to give a total voltage of 4.5V.
To find the voltage of each cell, we would need to know the voltage across each cell or the voltage of the other cells connected in the circuit. Then we could use the fact that the sum of the voltages across all cells in the circuit is equal to the total voltage of the circuit to solve for the voltage of each cell.
A recipe for 12 cookies calls for 1 1/3 cups milk, 2 1/2 cups flour, and 1 3/4 cups other ingredients. How many cups of milk, flour, and other ingredients are needed to make 24 cookies? *
Answers
Answer:
2 2/3 cups of milk, 5 cups of flour, 3 1/2 cups of other ingredients ;)
Find the midpoint of each line segment.

Answers
Answer:
(1.5, 0.5)
Step-by-step explanation:
(5, 3) and (-2, -2)
5 - 2 / 2 = 1.5
-2 + 3 / 2 = 0.5
Complete each statement. If the triangles cannot be shown to be congruent from the information given, leave the triangle's name blank and write Can not be Determined (CNBD) in the spot for rule.
By rule ________ ∆SAT ≅ Δ____ By rule ________
Answers
The completed statement that specifies the rule of congruency between triangle ΔSAT and triangle ΔSAO, is as follows;
ΔSAT ≅ ΔSAO by SAA rule.
What are congruent triangles?Two triangles, ΔA and ΔB are congruent if the three lengths of the sides of triangle ΔA are congruent to the three side lengths of triangle ΔB.
The possible dimensions of the triangles, obtained from the triangle diagrams in a similar question on the site are;
Side ST in triangle ΔSAT is congruent to side SO in triangle ΔSAO
Angle ∠AST in triangle ΔSAT is congruent to angle ∠ASO in triangle ΔSAO
Side SA is congruent to side SA by reflexive property of congruency
Therefore, a side, (ST) an included angle (∠AST) and another side (SA), in triangle ΔSAT are congruent to a side (SO), an included angle (∠ASO), and another side SA in triangle ΔSAO
Therefore, triangle ΔSAT is congruent to triangle ΔASO, by Side-Angle-Side, SAS, congruency ruleLearn more about the triangle congruency rules here:
https://brainly.com/question/3580004
#SPJ1

What is the answer to the question?

Answers
Answer:
the answer is option 4th
The student government snack shop sold 32 items this week.
For each snack type, what percentage of all snacks sold were of that type? Do not round your answers.

Answers
The percentages of each snack type that were sold are given as follows:
Fruit cup: 25%.Veggie sticks: 18.75%.Chips: 43.75%.Water: 12.5%.How to obtain the percentage?A percentage is one example of a proportion, as it is obtained by the number of desired outcomes divided by the number of total outcomes, and then multiplied by 100%.
Hence the percentages for each type are obtained as follows:
Fruit cup: 8/32 x 100% = 25%.Veggie sticks: 6/32 = 18.75%.Chips: 14/32 = 43.75%.Water: 4/32 = 12.5%.More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
Find the value of x, 6,4, 3x, 4x+1

Answers
Answer:
If two chords intersect in a circle, then the product of the segments of one chord equals the product of the segments of the other chord.
6(3x) = 4(4x + 1)
18x = 16x + 4
2x = 4
x = 2
sin(x)-cos(x)/sin²(x)-cos²(x) = 1

Answers
The prove of the given trigonometric function is given below.
The given trigonometric function is,
(sin⁴(x) - cos⁴(x))/(sin²(x) - cos²(x))
Now proceed left hand side of the given expression:
We can write the expression as,
⇒[(sin²(x))² - (cos²(x))²]/(sin²(x) - cos²(x))
Since we know that ,
Algebraic identity:
a² - b² = (a-b)(a+b)
Therefore the above expression be
⇒(sin²(x) - cos²(x))(sin²(x) + cos²(x))/(sin²(x) - cos²(x))
⇒(sin²(x) + cos²(x))
Since we know that,
Trigonometric Identities come in handy when trigonometric functions are used in an expression or equation. Trigonometric identities hold for all values of variables on both sides of an equation. Geometrically, these identities include one or more trigonometric functions (such as sine, cosine, and tangent).
Then,
sin²(x) + cos²(x)² = 1 is an trigonometric identity
Hence,
(sin⁴(x) - cos⁴(x))/(sin²(x) - cos²(x)) = 1
Hence proved.
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ1
What is the solution to |x-2| + 3 > 17?
Ox<-12 or x > 16
Ox<-14 or x>7
O-12
O-14
Answers
Answer:
x<-12 or x>16
Step-by-step explanation:
Answer:
|x - 2| + 3 > 17
|x - 2| > 14
x - 2 < -14 or x - 2 > 14
x < -12 or x > 16
Use the series below to answer the following questions
4(5)^k-1
1:A1= 4. R= 5. N=6.
2:a
3:15,624
Answers
The asked terms are a₁ = 4, r = 5 and n = 6 terms
What is a geometric sequence?A geometric sequence is a sequence in which each term is found by multiplying the preceding term by the same value.
Given that a sum of a geometric sequence, \(4(5)^{k-1}\),
We need to find the first term a₁, the common ration r, and the number of terms n,
The general formula for the geometric sequence, is given by :-
aₙ = a₁r⁽ⁿ⁻¹⁾
On comprising with the general formula with the given formula,
We get,
a₁ = 4
r = 5
n-1 = k-1
n = k
k is given 6,
therefore,
n = 6
Hence, the asked terms are a₁ = 4, r = 5 and n = 6 terms
Learn more about geometric sequence, click;
https://brainly.com/question/13008517
#SPJ9
The complete question is attached

what is the sum 3/x+9+5/x-9
Answers
Answer:
\(\frac{8}{x}\)
Step-by-step explanation:
what is the sum 3/x+9+5/x-9
\(\frac{3}{x} + 9 + \frac{5}{x} - 9 =\) (add \(\frac{3}{x}\) and \(\frac{5}{x}\))
\(\frac{8}{x} + 9 - 9 =\) (solve 9 - 9 = 0)
\(\frac{8}{x}\) ( your answer)
Please help.What are all the answers

Answers
Answer:
5.90=r, 6.67=can't see, 5.17=n, 5.34=o, 6.08=s, 6.83=can't see, 6.43=u, 5.01=m, 5.69=p
CF AND AH ARE SKEW PERPENDICULAR PARALLEL
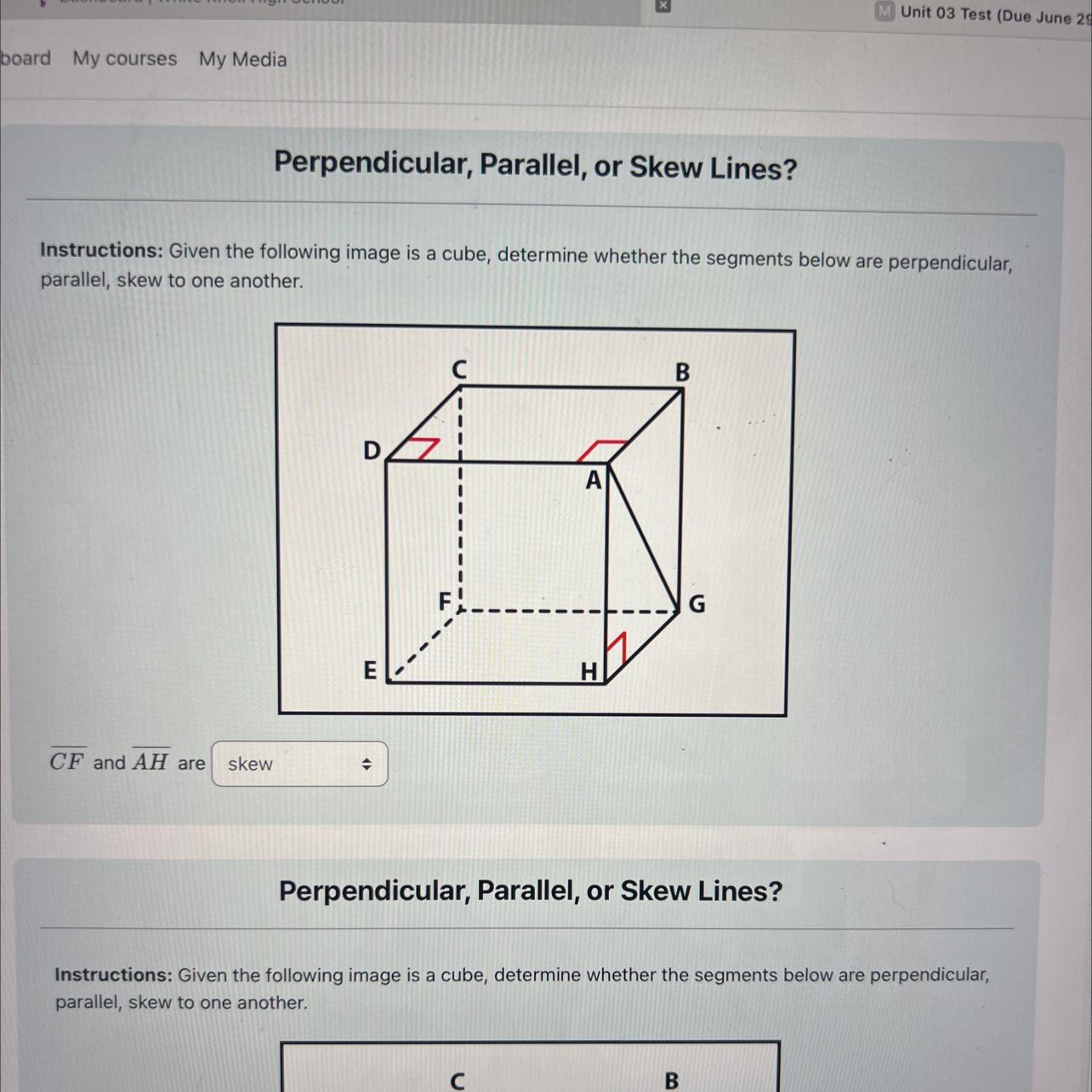
Answers
Reason: The two line segments CF and AH point in the same direction, and they never intersect. Therefore, we consider them parallel.
Skew lines are ones that point in different directions. An example of a pair of skew lines would be AB and DE. Skew lines never intersect, but we don't consider them parallel.
According to a 2011 publication, the average monthly expenditure of college students on coffee is $100. Given a standard deviation of $20, but with no confirmation of a normal distribution, what is the probability that the mean coffee expense of a randomly selected sample of 42 college students is greater than $90?
Answers
The Central Limit Theorem states that, given a sufficiently large sample size, the sampling distribution of the mean for a variable will approximate a normal distribution regardless of the underlying distribution of the variable. In this case, we have a sample size of 42, which is large enough for the Central Limit Theorem to apply.
The mean of the sampling distribution of the mean is equal to the population mean, which is $100. The standard deviation of the sampling distribution of the mean is equal to the population standard deviation divided by the square root of the sample size, which is $20 / sqrt(42) ≈ $3.08.
We can standardize to find the z-score for a sample mean of $90: z = ($90 - $100) / $3.08 ≈ -3.25. Using a z-table, we find that the probability of getting a z-score less than -3.25 is approximately 0.0006. Therefore, the probability that the mean coffee expense of a randomly selected sample of 42 college students is greater than $90 is approximately 1 - 0.0006 = 0.9994.
In this case, the sample size is 42, which is considered large enough for the Central Limit Theorem to apply. We can approximate the distribution of the sample mean using a normal distribution.
The mean of the sample means will still be $100, as it is the same as the population mean. However, the standard deviation of the sample means, also known as the standard error, is calculated by dividing the population standard deviation by the square root of the sample size. In this case, the standard error is $20 / √42 ≈ $3.08.
To find the probability that the mean coffee expense of a randomly selected sample of 42 college students is greater than $90, we need to calculate the z-score and then find the corresponding probability using a standard normal distribution table or calculator.
The z-score is calculated as follows:
z = (sample mean - population mean) / standard error
= ($90 - $100) / $3.08
≈ -3.25
Using the z-score of -3.25, we can find the corresponding probability from the standard normal distribution table or calculator. The probability will be the area to the right of the z-score, which represents the probability that the mean coffee expense is greater than $90.
Note that since the z-score is very negative, the probability will be very close to 1.
2 pounds 6 ounces = ounces
Answers
2 pounds 6 ounces in ounces is equivalent to 38 ounces.
The given measurement is -
2 pounds 6 ounces
In 1 pound, there are 16 ounces.
So, we can write that -
2 pounds 6 ounces = 2 x 16 + 6
2 pounds 6 ounces = 38 ounces
So, 2 pounds 6 ounces in ounces is equivalent to 38 ounces.
To solve more questions on unit conversion, visit the link-
brainly.com/question/11805053
#SPJ1
In the given figure the value of c is

Answers
Answer:
115
Step-by-step explanation:
So we can agree that x + x + 10 + 120 = 360
So if we simplify that we have 2x + 130 = 360
We subtract 130 from both sides 2x = 230
and divide by two x = 115
Help I Dont Understand?

Answers
a road rises 16 feet for every 50 feet of horizontal distance covered. in percent what is the grade of the road?
Answers
Answer:
32%
Step-by-step explanation:
The slope of the road is measured as
slope = \(\frac{rise}{run}\) = \(\frac{16}{50}\)
To express as a percentage multiply the fraction y 100% , that is
slope = \(\frac{16}{50}\) × 100% = 16 × 2 = 32%
Question 6
1 pts
A baby weighed 7.2 pounds at birth. Her weight was recorded at each of her infant
doctor appointments. The records for her appointments from birth to six months are
shown in the table below. Use the line of best fit to estimate the baby's weight at 1
year (12 months)?
Months
Weight (lbs)

Answers
Answer:
24.4
Step-by-step explanation:
Given the data :
Month (X) : 0, 1, 2, 4, 6
Weight (Y) : 7.2, 9.4, 10.5, 13.2, 15.9
To obtain the predicted weight at 1 year, we fit the data to obtain the regression model. Using technology, the regression model obtained is :
y = 7.6 + 1.4X1
Substituting x = 1 year into the regression model, we obtained the predicted weight at 1 year ;
1 year = 12 months, hence, x = 12
y = 7.6 + 1.4(12)
y = 7.6 + 16.8
y = 24.4
What is the Slope from graph

Answers
Answer:
3/4 I'm pretty sure that right
Help i dont understand this please help :(

Answers
Answer:
-16
Step-by-step explanation:
-5(4)+2
-18+2
-16
4) A line has a slope of -1 and a y-intercept of 6. Write its equation in slope-intercept form.
) Write your answer using integers, proper fractions, and improper fractions in simplest
form.
Answers
m is the slope.
b is the y-intercept.
Therefore, y=-1x+6
Two angles are complementary to each other. One angle measures 23°, and the other angle measures (6x − 20)°. Determine the value of x.
Answers
Answer:
15.5
Step-by-step explanation:
23-20=3
6x-3=90
3-90=93
93÷6=15.5
Answer:
14.5
Step-by-step explanation:
i got it right on the test
A survey of 800 randomly selected adults in a certain country found that 82% believed that
protecting the rights of those with unpopular views is a very important component of a strong
democracy.
a. Verify the Central Limit Theorem conditions.
b. Find a 95% confidence interval for the proportion of adults in the country who believe that
protecting the rights of those with unpopular views is a very important component of a strong
democracy.
c. Would a 90% confidence interval based on this sample be wider or narrower than the 95%
interval? Give a reason for your answer.
Answers
a) the Central Limit Theorem conditions are met. b) The 95% confidence interval for the proportion of adults who believe in protecting the rights of those with unpopular views is approximately 0.7934 to 0.8466.
c) . A 90% confidence interval would be wider than the 95% interval
How to Verify the Central Limit Theorem conditions.To verify the Central Limit Theorem (CLT) conditions, we need to check the following:
1. Random Sampling: The survey states that 800 adults were randomly selected, which satisfies this condition.
2. Independence: We assume that the responses of one adult do not influence the responses of others. This condition is met if the sample is collected using a proper random sampling method.
3. Sample Size: To apply the CLT, the sample size should be sufficiently large. While there is no exact threshold, a common rule of thumb is that the sample size should be at least 30. In this case, the sample size is 800, which is more than sufficient.
Therefore, the Central Limit Theorem conditions are met.
b. To find a 95% confidence interval for the proportion of adults who believe in protecting the rights of those with unpopular views, we can use the formula for calculating a confidence interval for a proportion:
CI = p ± z * √(p(1-p)/n)
where:
- p is the sample proportion (82% or 0.82 in decimal form).
- z is the z-score corresponding to the desired confidence level. For a 95% confidence level, the z-score is approximately 1.96.
- n is the sample size (800).
Calculating the confidence interval:
CI = 0.82 ± 1.96 * √(0.82(1-0.82)/800)
CI = 0.82 ± 1.96 * √(0.82*0.18/800)
CI = 0.82 ± 1.96 * √(0.1476/800)
CI = 0.82 ± 1.96 * √0.0001845
CI ≈ 0.82 ± 1.96 * 0.01358
CI ≈ 0.82 ± 0.0266
The 95% confidence interval for the proportion of adults who believe in protecting the rights of those with unpopular views is approximately 0.7934 to 0.8466.
c. A 90% confidence interval would be wider than the 95% interval. The reason is that as we increase the confidence level, we need to account for a larger margin of error to be more certain about the interval capturing the true population proportion. As a result, the interval needs to be wider to provide a higher level of confidence.
Learn more about confidence interval at https://brainly.com/question/73194
#SPJ1
If M is the set of all square numbers less than 80 and N is the set of all non-negative even numbers that are under 30, Write the lists of all elements of M and N.

Answers
Answer:
The set M of all square numbers less than 80 is:
M = {0, 1, 4, 9, 16, 25, 36, 49, 64}
The set N of all non-negative even numbers that are under 30 is:
N = {0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28}
Answer:
All elements of the set M in ascending order are:
1, 4, 9, 16, 25, 36, 49, 64All elements of the set N in ascending order are:
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28Step-by-step explanation:
A square number, also known as a perfect square, is a non-negative integer that is obtained by multiplying an integer by itself. In other words, it is the result of squaring an integer.
The square numbers less than 80 are:
1, 4, 9, 16, 25, 36, 49, and 64.An even number is an integer that is divisible by 2 without leaving a remainder.
The non-negative even numbers that are under 30 are:
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, and 28.Therefore:
All elements of the set M in ascending order are:
1, 4, 9, 16, 25, 36, 49, 64All elements of the set N in ascending order are:
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28