If a student thinks of a number from 1 to 75, what is the probability that the number will be 20, 30, or 40?If a student thinks of a number from 1 to 75, what is the probability that the number will be 20, 30, or 40?
Answers
Answer:
the probability is 3/75.
Related Questions
Please i need the answer fast k12
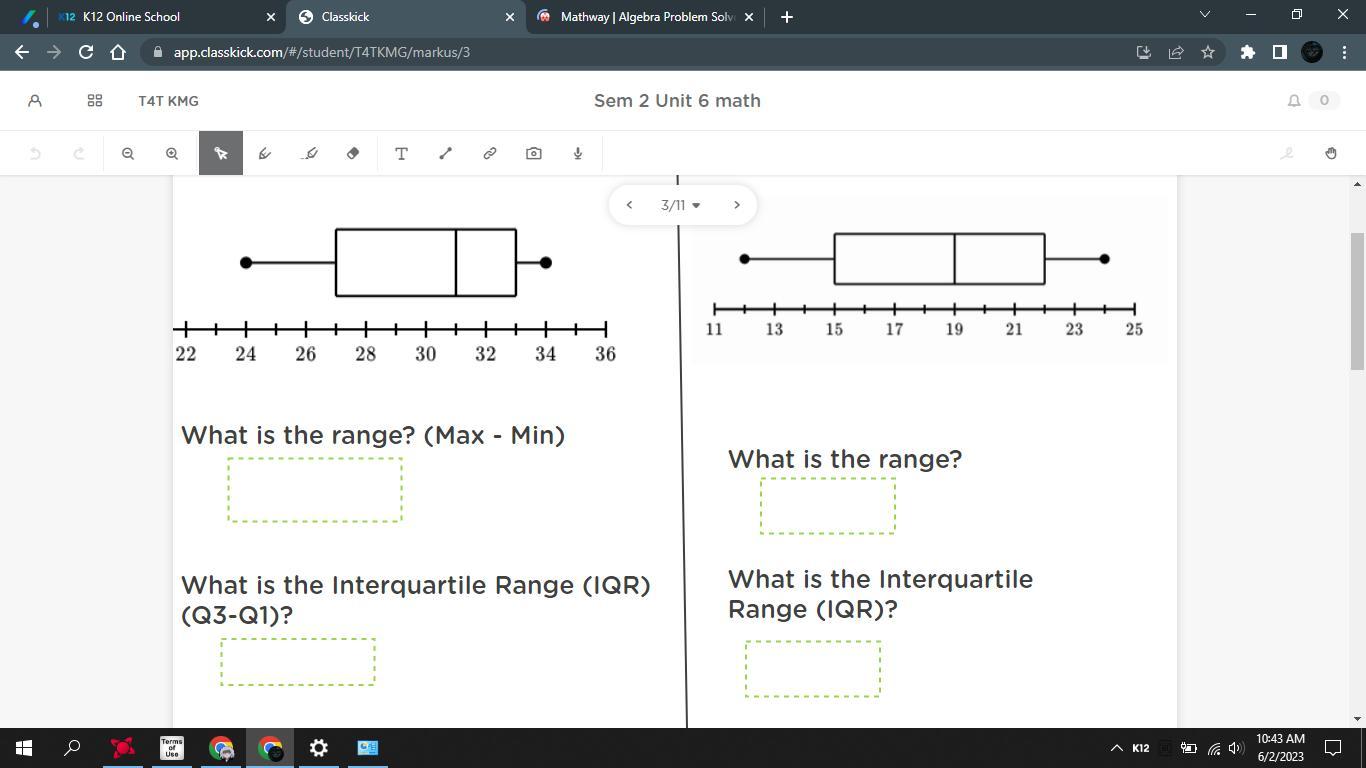
Answers
(A) The range and IQR for boxplot 1 is 10 and 6 respectively.
(B) The range and IQR for boxplot 2 is 12 and 7 respectively.
What is the IQR?The interquartile range defines the difference between the third and the first quartile.
The formula for the interquartile range is given below.
Interquartile range = Upper Quartile – Lower Quartile = Q3 – Q1
What is the range?The range is the difference between the lowest and highest values.
The formula for the interquartile range is given below.
Range = Maximum – Minimum
(A) For boxplot 1, we need to find the range and IQR from the given data set.
So, let 34 be the maximum and 24 be the minimum.
\(\text{Range}=\sf 34-24\)
\(\text{Range}=\sf10\)
Therefore, the range is 10.
Now time to find the IQR.
So, let 33 be Q3 and 27 be Q1.
\(\text{IQR}=\sf 33-27\)
\(\text{IQR}=\sf 6\)
Therefore, the IQR is 6.
(B) Now for boxplot 2, we will do the same thing as from part A.
Let's find the range.
So, let 24 be the maximum and 12 be the minimum.
\(\text{Range}=\sf 24-12\)
\(\text{Range}=\sf12\)
Hence, the range is 12.
Now for the IQR.
So, let 22 be Q3 and 15 be Q1.
\(\text{IQR}=\sf 22-15\)
\(\text{IQR}=\sf 7\)
Hence, the IQR is 7.
To know more about the range and IQR, visit:
https://brainly.com/question/31752116
#SPJ5
Assume a cube has side lengths of 2 inches. What is the area of the base of that cube? Does it matter which face we call the base? What is the volume of that cube? Instead, assume the cube has side lengths of 3 inches. What is the area of the base now? The volume? Based on that, what do you think the relationship is between side length, area, and volume? Would that still be true even if it is not a cube? (Put another way, if the side length is x, what is the area and volume?)
Answers
Answer:
Step-by-step explanation:
Volume of a cube:
V = a3
Surface area of a cube:
the area of each face (a x a) times 6 faces
S = 6a2
Face diagonal of a cube:
By the pythagorean theorem we know that
f2 = a2 + a2
Then f2 = 2a2
solving for f we get
f = a√2
Diagonal of the solid cube:
Again, by the pythagorean theorem we know that
d2 = a2 + f2
substituting f into this equation we get
d2 = a2 + (a√2)2 = a2 + 2a2 = 3a2
solving for d we get
d = a√3
A bucket contains six white balls and five red balls. A sample of four balls is selected
at random from the bucket, without replacement. What is the probability that the
sample contains...
Exactly two white balls and two red balls?
At least two white balls?
Answers
To solve this problem, we can use the formula for probability:
P(event) = number of favorable outcomes / total number of outcomes
First, let's find the total number of outcomes. We are selecting 4 balls from 11 without replacement, so the total number of outcomes is:
11C4 = (11!)/(4!(11-4)!) = 330
where nCr is the number of combinations of n things taken r at a time.
Now let's find the number of favorable outcomes for each part of the problem.
Part 1: Exactly two white balls and two red balls
To find the number of favorable outcomes for this part, we need to select 2 white balls out of 6 and 2 red balls out of 5. The number of ways to do this is:
6C2 * 5C2 = (6!)/(2!(6-2)!) * (5!)/(2!(5-2)!) = 15 * 10 = 150
So the probability of selecting exactly two white balls and two red balls is:
P(2W2R) = 150/330 = 0.45 (rounded to two decimal places)
Part 2: At least two white balls
To find the number of favorable outcomes for this part, we need to consider two cases: selecting 2 white balls and 2 red balls, or selecting 3 white balls and 1 red ball.
The number of ways to select 2 white balls and 2 red balls is the same as the number of favorable outcomes for Part 1, which is 150.
To find the number of ways to select 3 white balls and 1 red ball, we need to select 3 white balls out of 6 and 1 red ball out of 5. The number of ways to do this is:
6C3 * 5C1 = (6!)/(3!(6-3)!) * (5!)/(1!(5-1)!) = 20 * 5 = 100
So the total number of favorable outcomes for selecting at least two white balls is:
150 + 100 = 250
And the probability of selecting at least two white balls is:
P(at least 2W) = 250/330 = 0.76 (rounded to two decimal places)
10x-15y=35 I need help please!
Answers
Answer:
what help you need in this question
PLEASE HELP ME I WILL GIVE BRAINLEST

Answers
Help with this, thank you

Answers
The slope of a line perpendicular to the line whose equation is x - 2y = -8 is -2.
What are perpendicular lines?In Mathematics and Geometry, perpendicular lines are two (2) lines that intersect or meet each other at an angle of 90° (right angles).
From the information provided above, the slope for the equation of line m is given by:
x - 2y = -8
2y = x + 8
y = x/2 + 4
slope (m) of line m = 1/2
In Mathematics and Geometry, a condition that is true for two lines to be perpendicular is given by:
m₁ × m₂ = -1
1/2 × m₂ = -1
m₂ = -2
Slope, m₂ of perpendicular line = -2
Read more on perpendicular line here: brainly.com/question/27257668
#SPJ1
Use the histogram to answer the following questions.
Frequency
The frequency of the class 90-93 is
The frequency of the class 94-97 is
This means that a total of
5.5
5
4.5
Your answers should be exact numerical values.
The frequency of the class 86-89 is
86
94
90
Duration of Dormancy (minutes)
dormancy periods were recorded.
Answers
The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes, hence it is the same as a relative frequency.
The total number of periods is given as follows:
5 + 6 + 4 = 15.
The frequency of each class is given as follows:
86 - 89: 5/15 = 1/3.90 - 93: 6/15 = 2/5.94 - 97: 4/15.Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1

The perimeter of a rectangle is 34 feet. The length, l, of the garden is 14.38. the length, l, of the garden is 5 more than 2 times the width. Find the measurement of the width of the garden
Answers
The width of the garden is 4 feet.
What is Rectangle ?
A rectangle is a quadrilateral with four right angles, opposite sides that are parallel, and equal in length. It is a type of parallelogram where the adjacent sides are equal in length, but the opposite sides are not necessarily equal.
Let's start by using the formula for the perimeter of a rectangle:
Perimeter = 2(length + width)
We know that the perimeter is 34 feet, so we can plug in that value and simplify:
34 = 2(l + w)
17 = l + w
We also know that the length is 5 more than 2 times the width, so we can write an equation for that:
l = 2w + 5
We can substitute this expression for l into the first equation:
17 = (2w + 5) + w
Simplifying, we get:
17 = 3w + 5
12 = 3w
w = 4
Therefore, the width of the garden is 4 feet.
To learn more about Rectangle from given link.
https://brainly.com/question/15238546
#SPJ1
I need help with this it bob and Betty surviving people in there neighborhood on political opinion for their government class. they want know how long it take to do the survey survey responses 3 4 7 8 10 11collected total time. 7.5 10 17.5 20 25 27.5in minutes
Answers
To find the equation of the time they spent we need to use the:
\(y-y_1=m(x-x_1)\)Where m is the slope and (x1,y1) is a point of the table.
We can find the slope with:
\(m=\frac{y_2-y_1}{x_2-x_1}\)Using the first two points on the table we have:
\(\begin{gathered} m=\frac{10-7.5}{4-3} \\ =\frac{2.5}{1} \\ =2.5 \end{gathered}\)Now plugging the values of the slope and the first point into the equation we have that:
\(\begin{gathered} y-7.5=2.5(x-3) \\ y-7.5=2.5x-7.5 \\ y=2.5x \end{gathered}\)Therefore the equation that represents the time they spent is:
\(y=2.5x\)where x is the number of people they survey and y is the time it takes.
An experiment consists of recording, in order of their births, the sex composition of a four-child family in which the children were born at different times. (Let b represent the birth of a boy and g represent the birth of a girl. Enter your answers using letter combinations separated by commas. Example: bgbg, gggg, ...)
(a) Describe an appropriate sample space S for this experiment.
(b) Describe the event E that there are three boys and a girl in the family.
Answers
(a) An appropriate sample space S for this experiment is the set of all possible sequences of four children, where each child can be either a boy (b) or a girl (g). So, the sample space S is:
S = {bbbb, bbbg, bbgb, bgbb, gbbb, bggg, bgbg, gbgg, ggbb, gbgb, bggg, gbgg, gggg, gggb, gggg}
There are 2^4 = 16 possible outcomes in the sample space.
(b) The event E that there are three boys and a girl in the family can be represented by the set of all sequences in the sample space S that have three b's and one g. So, the event E is:
E = {bbbg, bbgb, bgbb, gbbb}
There are 4 possible outcomes in the event E.
Your taxable wages for Social Security purposes are $1100. How much is your Social Security tax if you have previous taxable wages of $102,000?
Answers
If you have previous taxable wages of $102,000 and your current taxable wages are $1,100, your Social Security tax would be $6,324 for the previous wages and $68.20 for the current wages.
To calculate the Social Security tax, we need to know the tax rate for Social Security and the taxable wages. Let's assume the Social Security tax rate is 6.2% for both the employee and the employer.
Given that your taxable wages for Social Security purposes are $1,100, and your previous taxable wages are $102,000, we can determine the Social Security tax amount.
First, we need to calculate the Social Security tax on the previous taxable wages of $102,000. Multiply $102,000 by 6.2% (0.062) to find the Social Security tax for that amount:
Social Security tax = $102,000 x 0.062 = $6,324
Next, we calculate the Social Security tax on the current taxable wages of $1,100. Multiply $1,100 by 6.2% to find the tax amount:
Social Security tax = $1,100 x 0.062 = $68.20
Therefore, if you have previous taxable wages of $102,000 and your current taxable wages are $1,100, your Social Security tax would be $6,324 for the previous wages and $68.20 for the current wages.
For more such answers on Tax
https://brainly.com/question/28414951
#SPJ8
the side of each square grid is 3 cm find the area of the figure a b c d
Answers
Answer:
a) 9 cm2
b) 12 cm2
c) 18 cm2
d) 27 cm2
what is 5 1/2 + 2 1/7 pleas help i cant figure it out
Answers
Answer:
\(\frac{107}{14}\) or \(7\frac{9}{14}\)
Step-by-step explanation:
\(5 \frac{1}{2} +2\frac{1}{7}\)
\(5 \frac{1}{2} +2\frac{1}{7} =\frac{11}{2} +\frac{15}{7}\)
\(\frac{11}{2} +\frac{15}{7}\)
\(\frac{11}{2} +\frac{15}{7}=\frac{77+30}{14} =\frac{107}{14}\)
\(\frac{107}{14} =7\frac{9}{14}\)
Hope this helps!
Fred is standing at a point looking north. He walks on a bearing 056° for 9.8km before stopping. He then walks an additional 3.5 km on a bearing of 112° before stopping to rest. (a) Find out how far he is away from his start point using sine or cosine rule (b) Determine the area of the enclosed shape (c) Draw neat labeled scale diagram of the same
Answers
The area of the enclosed shape is about 14.47 km^2.
We are given that;
056° for 9.8km and 3.5 km on a bearing of 112°
Now,
We can see that the enclosed shape is a triangle with sides 9.8 km, 3.5 km, and z km, and angles 56°, 112°, and y°. We can use the fact that the sum of angles in a triangle is 180° to find y:
y = 180° - 56° - 112°
y = 12°
Now we can use the cosine rule to find z:
z^2 = 9.8^2 + 3.5^2 - 2(9.8)(3.5)cos(12°)
z^2 ≈ 101.87
z ≈ 10.09
Therefore, Fred is about 10.09 km away from his start point.
To find the area of the enclosed triangle, we can use the sine rule to find x, the height of the triangle:
sin(56°) = x/9.8
x = 9.8 sin(56°)
x ≈ 8.27
The area of a triangle is given by half the base times the height, so:
A = (1/2)(3.5)(8.27)
A ≈ 14.47
Therefore, by trigonometric ratios the answer will be 14.47 km^2.
Learn more about trigonometric;
https://brainly.com/question/21286835
#SPJ1
What is the value of x?

Answers
Answer: x=70°
Step-by-step explanation:
These are supplementary angles, meaning they add up to 180°
45+(2x-5)=180°
45+2x-5=180
40+2x=180
2x=140
x=70°
HELPPP ASPA 60 POINT!!!!!Show to draw a line segment that measures 92 millimeters. i need it to be in words not a photo please
Answers
A line segment that measures 92 millimeters in length can be drawn using scale.
Given that,
A line segment has to be drawn which has a measure of length 92 millimeters.
We know that,
10 millimeters = 1 centimeter
1 millimeter = 1/10 centimeters
92 millimeters = 92/10 = 9.2 centimeters
So it is enough to draw a line segment of length 9.2 centimeters.
In the scale, between a centimeter, there are 9 small lines which indicates the millimeters.
In between 9 and 10, there are 9 lines which indicates, 9.1, 9.2, 9.3, ....., 9.9 and after that is 10 cm.
So draw a line segment starting from 0 to 9.2.
Hence the line segment is drawn with scale.
Learn more about Line Segments here :
https://brainly.com/question/9477630
#SPJ1
what's the inverse of f(x)=(x+3)^5
Answers
Answer:
The inverse is,
\(f^{-1}(x) = \sqrt[5]{x} - 3\)
Step-by-step explanation:
f(x) = (x+3)^5
Finding the inverse,
\(f(x) = (x+3)^5\\or,\\y = (x+3)^5\)
We replace x with y and vice versa
so,
\(x = (y+3)^5\)
Solving for y,
the the 5th root,
\(\sqrt[5]{x} = y + 3\\y = \sqrt[5]{x} - 3\)
hence the inverse function is,
\(f^{-1}(x) = \sqrt[5]{x} - 3\)
Step-by-step explanation:
f(x)=(x+3)×5
Y=5X+15
now
interxchanging x and y we get,
x=5y+15
5y=x-15
y=x-15/5
therefor f~1(x)=x-15/5
I need help with this problem asap :(

Answers
Answer:
m<P=130°
m<Q=130°
m<R=50°
Step-by-step explanation:
m<P=130
m<Q=130
m<R=50
What is total number?

Answers
Answer:
21 servings
Step-by-step explanation:
4/7 = 12/x
cross multiply and you get
4x = 7(12)
4x = 84
x = 21
• What is the total number of pencils that Mr. Moretti gives to his students
if he puts 3 mechanical pencils in each bag?
Answers
Answer:162
Step-by-step explanation:
162
A wireless keyboard is 10/12 foot long. The area of the wireless keyboard is 5/24 square foot. What is the width of the wireless keyboard, in feet? Enter the answer as a fraction in lowest
Answers
Answer:
1/4 ft
Step-by-step explanation:
A = l x w
5/24 = 10/12 x w
Solve for w
5/24 divided by 10/12 = w
Take inverse of 10/12 and multiply
5/24 times 12/10
1/4
PLEASE HELP I WILL MARK YOU BRAINIEST

Answers
i’m not 100% sure but i hope it’ll help
3x > 1
One cylinder has a volume that is 8 Centimeters cubed less than StartFraction 7 over 8 EndFraction of the volume of a second cylinder. If the first cylinder’s volume is 216 Centimeters cubed, what is the correct equation and value of x, the volume of the second cylinder?
StartFraction 7 over 8 EndFraction x + 8 = 216; x = 182 centimeters cubed
StartFraction 7 over 8 EndFraction x minus 8 = 216; x = 196 centimeters cubed
StartFraction 7 over 8 EndFraction x + 8 = 216; x = 238 centimeters cubed
StartFraction 7 over 8 EndFraction x minus 8 = 216; x = 256 centimeters cubed
Answers
Answer:
7/8X-8=216
x=256
7/8x-8=216
+8 +8
7/8x=224
7/8 7/8
x=256
Step-by-step explanation:
PLEASE HELP ASAP!! (Please do this if ur good at Scientific Notation) please tell me which 4 should I put in the box! (Click picture) ‼️‼️

Answers
Answer:
1st one is 6.9 X 10^6
2nd one is 2 x 10^5
Step-by-step explanation:
PLEASE ANSWER AS SOON AS POSSIBLE

Answers
Answer:
4 to 1
Step-by-step explanation:
Tablespoon of cocoa to Tablespoon of sugar
8 : 2
\(\frac{8}{2}\) : \(\frac{2}{2}\)
4 to 1
When recipe is doubled: ( 8 x 2) to (2 x 2)
16 : 4
\(\frac{16}{4}\) : \(\frac{4}{4}\)
4 to 1
It can be observed that the ratio remains the same
Function and notaion.

Answers
Answer: 45
Step-by-step explanation:
Function notation: is another way of writing a function to make it easy to understandInstead of the independent and dependent variables being x and y they are now x and f(x)f(x) can be interpreted as the y value at a given x value in this case f(-5) must be solved for, essentially saying what is y when the x value is -5\(f(-5)=2(-5)^{2} -5\)
\(f(-5)= 2(25) -5\)
\(f(-5) = 50-5\)
\(f(-5) = 45\)
different equation dy÷dx+ytanx=secx
Answers
Answer:
First, we rearrange the equation to isolate the y-term on one side:
dy/dx + ytanx = secx
Then, we multiply both sides by the integrating factor, which is e^(∫tanx dx) = e^(ln|secx|) = |secx|: | secx| dy/dx + ysecx tanx = 1
Next, we can write this as the derivative of a product using the product rule: d/dx (y |secx|) = 1
Integrating both sides with respect to x, we get: y |secx| = x + C
where C is the constant of integration. Solving for y, we have:
y = (x + C)/|secx|
Note that there is a singularity at x = (2n + 1)π/2, where the denominator |secx| is zero. At these points, the solution is not defined
A tent is in the shape of a triangular prism. It's length is 2.4m it's height 1.8m, and the width of the triangular end is 2.4m. Find the volume enclosed by the tent? how do I solve this?
Answers
Answer:
\(5.184m^3\)Explanation:
Here, we want to get the volume enclosed by the tent
Mathematically, that would be the product of the area of the triangular base and the height of the tent
We have the area of the traingular base as:
\(A\text{ =}\frac{1}{2}\times\text{ b}\times\text{ h = }\frac{1}{2}\times2.4\text{ }\times1.8=2.16m^2\)Finally,we muliply this by the height of the tent
We have this as:
\(2.16\text{ }\times2.4=5.184m^3\)The sum of eighteen and eight times a number is ninety.
what is the number?
Answers
Answer:
9
Step-by-step explanation:
9x8=72 72+18=90
Which of the following theorems verifies that abc wxy

Answers
Answer:
C. AA
Step-by-step explanation:
Since m<Y = 27°, then m<W = 27°.
We have two angles of one triangle (A and B) congruent to two angles of the other triangle (W and X).
Answer: C. AA