If a fraction between 0 and 1 is multiplied by another fl fraction between 0 and 1, the product is greater than 1
Answers
Answer: False
Step-by-step explanation: If you multiply a fraction between 0 and 1 by another fraction between 0 and 1, the result would be smaller than 1.
For example, \(\frac{3}{5} * \frac{1}{2} = \frac{3}{10}\)
Related Questions
Evaluate the following expression:
4a – 3b when a = – 3 and b = – 2
explain how you would get the answer above step by step
Answers
Answer:
-6
Step-by-step explanation:
4a-3b
Plug in a b
4(-3)-3(-2)
-12+6=-6
so 4a - 3b really means
4(-3) - 3(-2) then you solve
4 x -3 = -12
-3 x -2 = 6
-12 - 6 = -18
-18 is your answer
The reference angle for 5 is 1, which has a terminal point ofWhat is the terminal point of 51?√2/22 3 2

Answers
Then the terminal point of 5pi/4 will be the pair of negatives of the terminal point od pi/4, it will be:
\((-\frac{\sqrt[]{2}}{2},-\frac{\sqrt[]{2}}{2})\)which is the option B in the list.

Winning the jackpot in a particular lottery requires that you select the correct two numbers between 1 and 59 and in a separate drawing you must also select the correct single number between 1 and 30 find the probability of winning the jackpot
Answers
Winning the jackpot in a certain lottery requires you to pick two correct numbers between 1 and 59, and in a separate drawing, you also have a 7.32397915e-8 chance of winning when you also pick one correct number between 1 and 30.
A number of ways to select r items from n, nCr = n!/(r! x (n - r)!)
Number of possible methods to choose 4 winning numbers from 59 = 59C4
= 59!/(55! x 4!)
= 455,126
The number of possible ways to choose a single accurate number from 30 = 30.
The odds of winning the jackpot are 1/(probability) (Number of ways in which 4 winning numbers can be selected from 59 x Number of ways in which the correct single number can be selected from 30)
= 1/(455,126 x 30)
= 1/13653780
= \(7.32397915^{8}\)
To learn more about probability
https://brainly.com/question/11234923
#SPJ1
Need help with This assignment asap will mark brainless

Answers
Answer:
Hello,
Answer: B : y=(m-3)*(x+1)²3
Step-by-step explanation:
The parabola with vertex (-1,3)
is y=k(x+1)²+3
(0,m) is a point of the parabola:
m=k*(0+1)²+3 ==> k=m-3
So, y=(m-3)*(x+1)²+3 is the correct equation.
Which linear function has the same y-intercept as the one that is represented by the graph?
On a coordinate plane, a line goes through points (3, 4) and (5, 0).
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 3, negative 1, 1, 3. Column 2 is labeled y with entries negative 4, 2, 8, 14.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 4, negative 2, 2, 4. Column 2 is labeled y with entries negative 26, negative 18, negative 2, 6.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 5, negative 3, 3, 5. Column 2 is labeled y with entries negative 15, negative 11, 1, 5.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 6, negative 4, 4, 6. Column 2 is lab
eled y with entries negative 26, negative 14, 34, 46.
Answers
The linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
To determine the linear function with the same y-intercept as the graph, we need to find the equation of the line passing through the points (3, 4) and (5, 0).
First, let's find the slope of the line using the formula:
slope (m) = (change in y) / (change in x)
m = (0 - 4) / (5 - 3)
m = -4 / 2
m = -2
Now that we have the slope, we can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Using the point (3, 4) as our reference point, we have:
y - 4 = -2(x - 3)
Expanding the equation:
y - 4 = -2x + 6
Simplifying:
y = -2x + 10
Now, let's check the given options to find the linear function with the same y-intercept:
Option 1: The table with x-values (-3, -1, 1, 3) and y-values (-4, 2, 8, 14)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 2: The table with x-values (-4, -2, 2, 4) and y-values (-26, -18, -2, 6)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 3: The table with x-values (-5, -3, 3, 5) and y-values (-15, -11, 1, 5)
The y-intercept is the same as the given line (10). So, this option is correct.
Option 4: The table with x-values (-6, -4, 4, 6) and y-values (-26, -14, 34, 46)
The y-intercept is not the same as the given line. So, this option is not correct.
Therefore, the linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
for such more question on linear function
https://brainly.com/question/9753782
#SPJ8
a certain number is written on the blackboard. One student increased that number by 23, and the other decreased it by 1. It turned out that the result of the first one is 7 times greater than the result of the second one. What number was written on the blackboard?
Answers
The number written on the board will be negative 27. This can be solved by using the concept of algebra.
What is Algebra?Algebra is the study of mathematical symbols, while logic is the manipulation of those symbols.
Let x be the number.
There is a number written on the board. One student increased the number by 23. Then the first number will be
⇒ x + 23
But another student decreased the same number by 1. Then the second number will be
⇒ x - 1
The first student's result was 7 times greater than the result of the second student.
7 first number = second number
or, 7(x + 23) = x - 1
or, 7x + 161 = x - 1
or, 6x = - 162
or, x = - 27
The number written on the board will be negative 27.
To learn more about the Algebra refer to:
brainly.com/question/953809
#SPJ1
Here are the heights (in inches) of 12 students in a seminar. 71, 67, 62, 60, 70, 64, 68, 72, 58, 63, 60, 66 What is the percentage of these students who are shorter than 65 inches? 1% X 5
Answers
25% of the students in the seminar are shorter than 65 inches.
To find the percentage of students who are shorter than 65 inches, we first need to find the number of students whose height is less than 65 inches:
There are three students who are shorter than 65 inches: 62, 60, and 58.
Therefore, the percentage of students who are shorter than 65 inches is:
(3 students / 12 students) × 100% = 25%
Note that the value given for 1% × 5 does not appear to be relevant to this question, and is not necessary for the calculation of the percentage of students who are shorter than 65 inches.
For such more questions inches
https://brainly.com/question/876758
#SPJ8
Which costs less: a $52 jacket at 15% off or a $56 dollar jacket at 20% off? How much less?
Answers
Answer:
The $52 jacket by 60(0.60) cents.
Step-by-step explanation:
To find how much percent off is each item. We would need to multiply 52 by 0.85 and 56 by 0.80. The work is below:
52*0.85=44.2
56*0.80=44.8
We can say that the $52 jacket costs less than the $56 jacket by a difference of 60(0.60) cents.
Hope this helps!!! PLZ MARK BRAINLIEST!!!
Two or more angles whose measures add up to equal 90 degrees are called
angles.
Answers
Explanation: Angles that add up to a 90 degree measurement are called complementary angles.
Example: 25 degrees and 65 degrees
when a slice of buttered toast is accidentally pushed over the edge of a counter, it rotates as it falls. suppose the distance to the floor is 82 cm and the toast rotates less than 1 rev.
Answers
(i) The smallest angular speeds that cause the toast to hit and then topple to be butter-side down 3.84 rad / s
(ii) The largest angular speeds that cause the toast to hit and then topple to be butter-side down 11.51 rad / 5
The distance from the counter to the floor, d = 82 cm = 0.82 m
Rotation is less than 1 rev.
The toast rotates at a constant angular speed as it falls, and the toast is falling with a constant acceleration (gravitational acceleration).
Using the kinematic equations of motion to calculate the time taken by the toast to hit the floor
\($d & =v_i t+\frac{1}{2} g t^2 \\\)
\($d & =0+\frac{1}{2} g t^2 \\\)
Therefore \($t & =\sqrt{\frac{2 d}{g}}=\sqrt{\frac{2 \times 0. 82}{9.8}\)
= 0.409 s
Where
\($v_i$\) is the initial speed of the toast, \($v_i=0$\) because the toast is falling from rest.
t the time that the toast takes to hit the floor.
g is the gravitational acceleration.
d is the distance between the counter and the floor.
Part (a)The toast is accidentally pushed over the edge of the counter with the butter side up, then the toast rotates as it falls. If the toast hits the ground and then topples to be butter-side down, it has to land on one of its edges. The smallest angle, in this case, is \($\frac{1}{4}$\) revolution and corresponds to the smallest angular speed
\($\omega_{\min } & =\frac{\Delta \theta}{\Delta t} \\\)
\($\omega_{\min } & =\frac{0.25 \mathrm{rev}}{\Delta t}=\frac{0.25 \times 2 \pi}{\Delta t} \\\)
Therefore \($ \omega_{\min } & =\frac{0.5 \pi}{0.409}\)
= 3.84 rad/s
Where
\($\omega_{\min }$\) is the minimum angular speed for the toast to land butter-side down. \($\Delta \theta$\) is the smallest angle for the toast to land butter-side down in radians.
\($\omega_{\min }$\) = 3.84 rad / s
Part b:
The toast is accidentally pushed over the edge of the counter with the butter side up, then the toast rotates as it falls. If the toast hits the ground and then topples to be butter-side down, it has to land on one of its edges. The largest angle, in this case, is \($\frac{3}{4}$\) revolution and corresponds to the largest angular speed
\($\omega_{\max } & =\frac{\Delta \theta}{\Delta t} \\\)
\($\omega_{\max } & =\frac{0.75 \mathrm{rev}}{\Delta t}=\frac{0.75 \times 2 \pi}{\Delta t} \\\)
Therefore \($ \omega_{\max } & =\frac{1.5 \pi}{0.409}\)
= 11.51 rad / s
For more questions on angular speed
https://brainly.com/question/13785503
#SPJ4
When a slice of buttered toast is accidentally pushed over the edge of a counter, it rotates as it falls. If the distance to the floor is 82 cm and for rotation less than 1 rev, what are the (i) smallest and (ii) largest angular speeds that cause the toast to hit and then topple to be butter-side down?
How tall is the tree?
5ft
35°
-20ft-
[?]ft
Round to the nearest foot.
Answers
Answer:
19
Step-by-step explanation:
tan35=x/20
20tan35=x
x=14.0041507641942
x+5=19.0041507641942
The nearest foot is 19
Joy borrowed $2,000 from the bank and agreed to pay an annual interest rate of 6%for 24 months. What is the amount Of interest she will pay on this loan?
Answers
Answer:
2,240
Step-by-step explanation:
6% of 2,000 is 120 so times that by 2
Answer:
$240.00
Step-by-step explanation:
2000(.06)(2)=240
Nikhil and Mae work at the same company. Nikhil has been at the company 4 times as long as Mae. Nikhil's time at the company is 8 more than 2 times Mae's time. The following system of equations models the scenario: x = 4y x = 8 + 2y How many years has each person been employed by the company? Nikhil has been with the company for 16 years, while Mae has been there for 4 years. Nikhil has been with the company for 24 years, while Mae has been there for 6 years. Nikhil has been with the company for 20 years, while Mae has been there for 5 years. Nikhil has been with the company for 12 years, while Mae has been there for 3 years
Answers
The number of years of employment is A. Nikhil has been with the company for 16 years, while Mae has been there for 4 years.
How to find the years of employment ?The system of equations given is:
x = 4y
x = 8 + 2y
You can solve the system by setting the two expressions for x equal to each other:
4y = 8 + 2y
2y = 8
2y / 2 = 8 / 2
y = 4
Substitute y = 4 into the first equation to solve for x:
x = 4 x 4
= 16
So, Mae (y) has been at the company for 4 years and Nikhil (x) has been at the company for 16 years.
Find out more on system of equations at https://brainly.com/question/3978002
#SPJ1
2. 7 cm In triangle ABC, AC = 7 cm, BC = 10 cm, angle ACB = 73° C 73° 10 cm Calculate the length of AB Give your answer correct to 3 significant figures. Diagram NOT accurately drawn B (Total 3 marks

Answers
Answer:
AB = 10.398
Step-by-step explanation:
By cosine rule, we have:
AB² = AC² + BC² - 2(AC)(BC)cos(ACB)
⇒ AB² = 7² + 10² - 2(7)(10)cos(73)
⇒ AB² = 49 + 100 - 140cos(73)
⇒ AB² = 149 - 140cos(73)
⇒ AB² = 149 - 140cos(73)
⇒ AB² = 149 - 140(0.292)
⇒ AB² = 149 - 40.88
⇒ AB² = 108.12
⇒ AB = √(108.12)
⇒ AB = 10.398
expand and simplify (x+5)(x-1)
Answers
The expanded and simplified form of the expression (x + 5)(x - 1) is x² - x + 5x - 5.
What is the expanded form of the expression?Given the expression in the question;
(x + 5)(x - 1)
To expand and simplify the expression (x+5)(x-1),
we use the distributive property:
(x + 5)(x - 1)
x(x - 1) + 5(x - 1)
Now we can simplify each term by using the distributive property again:
x(x - 1) = x² - x
5(x - 1) = 5x - 5
Putting these terms back together, we have:
(x+5)(x-1) = x² - x + 5x - 5
Combining like terms, we get:
(x+5)(x-1) = x² + 4x - 5
Therefore, (x+5)(x-1) simplifies to the quadratic expression x² + 4x - 5.
Learn more about distributive property here: https://brainly.com/question/13130806
#SPJ1
Follow the instructions to find out what number you end up with.

Answers
=========================================================
Explanation:
"Decrease the number by 4 tenths" means we're subtracting off 0.4"Increase the number by 8 thousandths" means we're adding 0.008"Increase the number by 2 tens" is the same as adding on 2*10 = 20The changes of this number are
-0.4+0.008+20The overall net change is -0.4+0.008+20 = 19.608
We'll be adding this net change to the original number
143.351 + 19.608 = 162.959
This value is exact and hasn't been rounded.
There are 5 red marbles, 8 blue marbles, and 12 green marbles in a bag.
What is the theoretical probability of randomly drawing a red marble?
25%
62.5%
20%
41.7%
Answers
Answer:
20%
Step-by-step explanation:
The theoretical probability of drawing a red marble can be found by dividing the number of red marbles by the total number of marbles in the bag:
P(red) = number of red marbles / total number of marbles
P(red) = 5 / (5 + 8 + 12)
P(red) = 5 / 25
P(red) = 0.2
So the theoretical probability of randomly drawing a red marble is 20%, which corresponds to option (C).
A rectangle is bounded by the x- and y-axes and the graph of y= (6 - x)/2 (see figure). What length (x) and width (y) should the rectangle have so that its area is a maximum?

Answers
The rectangle with largest area has length 3 and width 3/2, with an area of 9/2.
What is a rectangle?
A rectangle is a sort of quadrilateral with parallel sides that are equal to one another and four vertices that are all 90 degrees apart. As a result, it is sometimes referred to as an equiangular quadrilateral. Because the opposing sides of a rectangle are equal and parallel, it can also be referred to as a parallelogram.
The equation for the area of a rectangle is length * width. For us here, it would be x * y. We can substitute the equation of the line for y and get
A = x * (6-x)/2
A = 3x - x2/2
To find the maximum of this equation, we first need to find a critical point. So we take the derivative and find the zeros:
A' = 3 - x = 0
x = 3
So we have a critical point at 3, which happens to be the maximum of the area equation. We plug this back into the line equation to get y:
y = (6 - 3)/2 = 3/2
So the rectangle with largest area has length 3 and width 3/2, with an area of 9/2.
Learn more about rectangle
brainly.com/question/29123947
#SPJ1
Hey can someone please help me out? I’ll appreciate it tysm :)

Answers
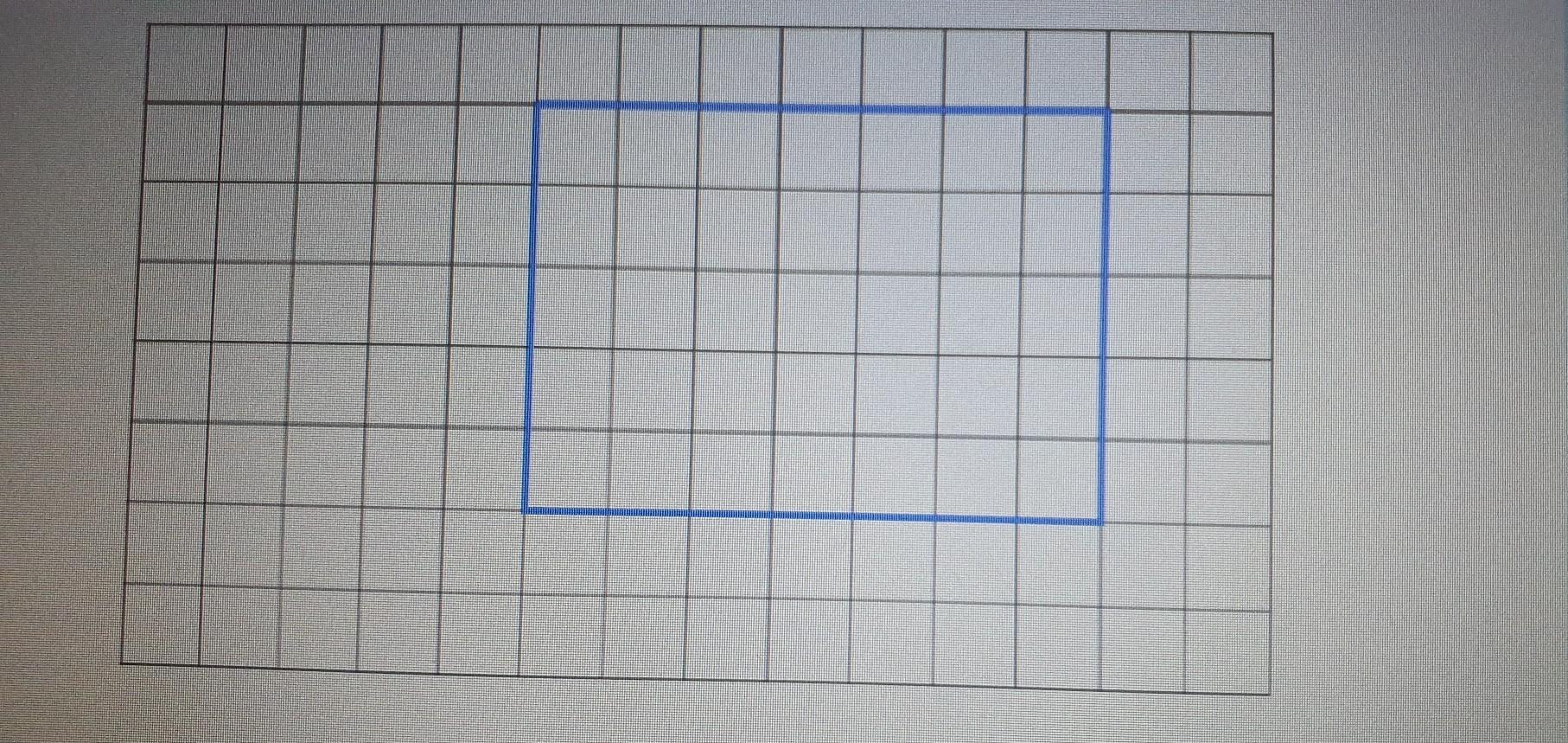
Find the area of the rectangle on this centimetre grid.
Answers
Answer:
A = 35 cm²
Step-by-step explanation:
the area (A) of a rectangle is calculated as
A = length × width
by counting the squares on the sides
length = 7 cm and width = 5 cm , then
A = 7 × 5 = 35 cm²
Philip has been experimenting with new recipes at his bakery for the past 8 months. This month, he tried a recipe for lavender vanilla muffins and gave samples to his customers. He asked them to rate the muffins on a scale of 1 to 10 stars. The median rating was 7 stars, and the interquartile range was 4 stars. ) What can you conclude from these data and statistics? Select all that apply. () No customer gave the muffins fewer than 8 stars. A typical rating for the muffins was 7 stars. The middle 50% of customer ratings had a range of 4 stars. Submit
Answers
- A typical rating for the muffins was 7 stars, since the median rating was 7 stars.
- The middle 50% of customer ratings had a range of 4 stars, since the interquartile range was 4 stars.
- We cannot conclude that no customer gave the muffins fewer than 8 stars, as the median is not necessarily equal to the mean, and it is possible that some customers rated the muffins below 8 stars. Therefore, this statement is not necessarily true.
The city manager made a scatter plot of the number of retail stores in a
city over many years. The trend line for the scatter plot has the equation y =
11x + 12, where y is the total number of stores and x is the number of years
after 1990. Predict how many retail stores there were in 1997.
Answers
Answer:
There were 89 retail stores in 1997.
Step-by-step explanation:
You know:
y = 11*x + 12
where y is the total number of stores and x is the number of years after 1990.
Being this a linear function (Linear functions are those functions that have the form y = mx + b as it happens in this case), to know the total number of stores and, then you must know the value of x, that is, the number of years after 1990, and replace that value in the given function.
To find out how many retail stores there were in 1997, then since 1990 7 years have passed, calculated by subtracting: 1997 - 1990 = 7
So, 7 is the number of years after 1990, then x=7
Replacing in the function y=11*x + 12 you get:
y=11*7+12
Solving:
y=77+12
y=89
There were 89 retail stores in 1997.
lynn had 14 grapes. she ate 8 of them. she wants to eat 6 more grapes. will lynn have enough grapes? Explain.
Answers
Yes she will be left with 0 grapes
Step-by-step explanation:
14-8=6 6-6=0
Explanation: 14-8=6-6=0 6+8=14
3(2x+1)=7x-2 find the value of x
Answers
Answer:
5
Step-by-step explanation:
3(2x+1)=7x-2
6x + 3 = 7x - 2
6x - 7x = -2 - 3
-x = -5 /(-1)
x = 5
Answer:
5
Step-by-step explanation:
3 ( 2x + 1 ) = 7x - 2
Step 1 : Remove the parentheses
6x + 3 = 7x - 2
Step 2 : Move the variable to the left-hand side and move extra number the right-hand side
6x + 3 = 7x - 2
-7x -3 -7x -3
6x - 7x = -2 - 3
Step 3 : Combine like terms
-x = -5
Step 4 : Change the sign to make x positive
x = 5
SOLUTION : x = 5
Hope this helps :)
What is the approximate area of the shaded sector in the circle shown below
A.29.04 in^2
B.13.51 in^2
C.7.26 in^2
D.6.75^2
Answers
Answer:
please provide the diagram
Step-by-step explanation:
for the solution figure is necessary so provides us to solve this problem
Find the length of MT.

Answers
Answer:
\(5.24\mathrm{cm}\)
Step-by-step explanation:
\(\mathrm{Solution:}\\\mathrm{Given:}\\\mathrm{Angle\ subtented\ by\ arc\ MT}(\theta)=100^o=\frac{5}{9}\pi^c\\\mathrm{Length\ of\ arc\ MT}(l)=?\\\mathrm{Radius\ of\ circle}(r)=3cm\\\mathrm{Now,}\\\mathrm{\theta=}\frac{l}{r}\\\mathrm{or,\ }l=\theta r=\frac{5}{9}\pi\times3=\frac{5}{3}\pi=5.24\mathrm{cm}\)
A shipping box is 36 inches by 24 inches by 18 inches
how many cubic feet can it hold
Answers
Answer:
To find the volume of the shipping box in cubic feet, we need to convert the dimensions from inches to feet and then calculate the volume.
Given:
Length = 36 inches
Width = 24 inches
Height = 18 inches
Converting the dimensions to feet:
Length = 36 inches / 12 inches/foot = 3 feet
Width = 24 inches / 12 inches/foot = 2 feet
Height = 18 inches / 12 inches/foot = 1.5 feet
Now, we can calculate the volume of the box by multiplying the length, width, and height:
Volume = Length * Width * Height
Volume = 3 feet * 2 feet * 1.5 feet
Volume = 9 cubic feet
Therefore, the shipping box can hold 9 cubic feet.
Step-by-step explanation:
First convert the units because it's asking for the cubic feet but they give us the measurements in inches.
To convert inches to feet we divide the number by 12.
36 ÷ 12 = 3
24 ÷ 12 = 2
18 ÷ 12 = 1.5
Now to find the volume, we multiply it all together.
3 × 2 × 1.5 = 9
It can hold 9 cubic feet.
Hope this helped!
What is the equation of this line?
y= - 3/2x
y= 3/2x
y= - 2/3x
y= 2/3x

Answers
Answer:
\(y=\displaystyle\frac{2}{3}x\)
Step-by-step explanation:
Hi there!
The given linear equations are organized in slope-intercept form: \(y=mx+b\) where m is the slope of the line and b is the y-intercept (the value of y when x=0)
First, we can determine the slope using the following formula:
\(m=\displaystyle\frac{y_2-y_1}{x_2-x_1}\) where two given points are \((x_1,y_1)\) and \((x_2,y_2)\)
Plug in any two points from the graph that falls on the line (you can see below that I've used (3,2) and (0,0):
\(m=\displaystyle\frac{2-0}{3-0}\\\\m=\displaystyle\frac{2}{3}\)
Therefore, the slope of the line is \(\displaystyle\frac{2}{3}\). Plug this into \(y=mx+b\) as m:
\(y=\displaystyle\frac{2}{3}x+b\)
We know that the point (0,0) falls on the line. Because y=0 when x=0, we know that the y-intercept (b) is 0:
\(y=\displaystyle\frac{2}{3}x+0\\\\y=\displaystyle\frac{2}{3}x\)
I hope this helps!
What is the maximum product of two numbers that add to 24?
Answers
Let x and y represent the two numbers that add up to 24.
x + y = 24
=> y = 24 - x
The product of the two numbers is P = x*y = x*(24 - x) = 24x - x^2.
To maximize the product P, solve P' = 0 for x.
P' = 24 - 2x
24 - 2x = 0
=> x = 12
Also P'' = -2 which is negative
for x = 12
The product when x = 12 is 12*12 = 144
hope it helps!
On a coordinate plane, a dashed straight line has a positive slope and goes through (negative 3, negative 3) and (3, 1). Everything below and to the right of the line is shaded.
Which linear inequality is represented by the graph?
y > Two-thirdsx – 2
y < Two-thirdsx + 2
y > Two-thirdsx + 1
y < Two-thirdsx – 1
Answers
Answer:
y > Two-thirds x + 1 /c