if 75 percent of the guests at a certain banquet ordered dessert, what percent of the guests ordered coffee?
Answers
Therefore, we cannot determine the percentage of guests who ordered coffee from the information provided in either statement alone.
What is percent?Percent is a way of expressing a quantity as a fraction or a ratio of 100. The word "percent" means "per hundred." It is denoted by the symbol % and is used to describe a portion or a fraction of a whole, where 100% represents the whole. For example, if 40 out of 100 students in a class passed an exam, we can say that 40% of the students passed. Percentages are commonly used in everyday life, finance, and mathematics to represent changes, discounts, taxes, and interest rates.
Here,
Using the information provided in the statements:
(1) If 60 percent of the guests who ordered dessert also ordered coffee, we can determine that 60 percent of the 75 percent who ordered dessert also ordered coffee. That means that 0.60 x 0.75 = 0.45, or 45 percent of the guests ordered both dessert and coffee. However, this information alone does not tell us how many guests ordered coffee in total, as some guests who did not order dessert could have still ordered coffee.
(2) If 90 percent of the guests who ordered coffee also ordered dessert, we can determine that 90 percent of the guests who ordered coffee ordered dessert. However, we cannot determine how many guests in total ordered coffee, as some guests who did not order dessert may have still ordered coffee.
To know more about percent,
https://brainly.com/question/29172752
#SPJ1
Related Questions
use cylindrical coordinates. evaluate x2 dv, e where e is the solid that lies within the cylinder x2 y2 = 4, above the plane z = 0, and below the cone z2 = 36x2 36y2.
Answers
Using cylindrical coordinates ∫∫∫ (r^3cos^2θ) dz dr dθ, where r ranges from 0 to 2, θ ranges from 0 to 2π, and z ranges from 0 to √(36r^2).
To evaluate the integral ∫∫∫ x^2 dV over the solid e, using cylindrical coordinates, we need to express the integral in terms of cylindrical coordinates and determine the appropriate bounds for the variables.
In cylindrical coordinates, the solid e can be defined as follows:
Radius: r ranges from 0 to 2 (from x^2 + y^2 = 4, taking the square root).
Angle: θ ranges from 0 to 2π (full revolution around the z-axis).
Height: z ranges from 0 to the height of the cone, which is determined by z^2 = 36x^2 + 36y^2.
To convert the integral, we need to express x^2 in terms of cylindrical coordinates:
x^2 = (rcosθ)^2 = r^2cos^2θ
The integral in cylindrical coordinates becomes:
∫∫∫ (r^2cos^2θ) r dz dr dθ
Now we can determine the bounds for the variables:
r ranges from 0 to 2.
θ ranges from 0 to 2π.
z ranges from 0 to the height of the cone, which can be determined by setting z^2 = 36r^2.
Substituting the bounds and integrating, we can evaluate the integral to find the desired result.
To know more about cylindrical coordinates refer here:
https://brainly.com/question/30394340
#SPJ11
\(52 \times 749 = \)
what is 52 x 749=
Answers
1. Give the formula for the forward Fourier Transform for a signal, X(jω)=F{x(t)}. 2. Give the formula for the inverse Fourier Transform of a signal, x(t)=F−1{X(jω)}. Compare this to the formula from problem 1) above and discuss similarities and differences. What is the Fourier Transform property called which refers to the similarity between the two formulas? 3. Using the defining integral of the Fourier Transform, determine the transform of the following signal: x(t)=⎣⎡−1,1,0,−1
Answers
The forward Fourier Transform formula for a signal is X(jω) = F{x(t)}. The inverse Fourier Transform formula is x(t) = F^(-1){X(jω)}. The two formulas are related by the Fourier Transform property called duality or symmetry.
1. The forward Fourier Transform formula is given by:
X(jω) = ∫[x(t) * e^(-jωt)] dt
This formula calculates the complex spectrum X(jω) of a signal x(t) by integrating the product of the signal and a complex exponential function.
2. The inverse Fourier Transform formula is given by:
x(t) = (1/2π) ∫[X(jω) * e^(jωt)] dω
This formula reconstructs the original signal x(t) from its complex spectrum X(jω) by integrating the product of the spectrum and a complex exponential function.
The similarity between these two formulas is known as the Fourier Transform property of duality or symmetry. It states that the Fourier Transform pair (X(jω), x(t)) has a symmetric relationship in the frequency and time domains. The forward transform calculates the spectrum, while the inverse transform recovers the original signal. The duality property indicates that if the spectrum is known, the inverse transform can reconstruct the original signal, and vice versa.
3. To determine the Fourier Transform of the given signal x(t) = [-1, 1, 0, -1], we apply the defining integral:
X(jω) = ∫[-1 * e^(-jωt1) + 1 * e^(-jωt2) + 0 * e^(-jωt3) - 1 * e^(-jωt4)] dt
Here, t1, t2, t3, t4 represent the respective time instants for each element of the signal.
Substituting the time values and performing the integration, we can obtain the Fourier Transform of x(t).
Note: Please note that without specific values for t1, t2, t3, and t4, we cannot provide the numerical result of the Fourier Transform for the given signal. The final answer will depend on these time instants.
Learn more about Fourier here:
https://brainly.com/question/33191499
#SPJ11
a circular pool is surrounded by a brick walkway 3 m wide. find the ra- dius of the pool if the area of the walk- way is 198 m*.
Answers
The radius of the pool is 9.01 m.
Given,
In the question:
A circular pool is surrounded by a brick walkway 3 m wide.
The area of the walk- way is 198 m^2.
To find the Radius of the pool.
Now, According to the question:
"Area of the circle bounded by the outside edge of the walkway" minus "area of the pool" = "area of the walkway".
Let R = Radius of the pool
Area of the circle bounded by the outside edge of the walkway is:
\(\pi\)(R +3)^2
Area of the pool is:
\(\pi R^2\)
Now, Our equation is:;
\(\pi\)(R +3)^2 - \(\pi R^2\) = 198
\(\pi\)((R+3)^2 - \(R^2\)) = 198
Open the inner bracket :
\(\pi\)(\(R^2+6R+9-R^2\)) = 198
\(\pi\)(6R +9) = 198
6R+9 = 198/\(\pi\)
6R = 198/\(\pi\) - 9
R = (198/\(\pi\) - 9)/6
R = (198/(3.14) - 9)/6
R = (63.057 - 9)/6
R = 54.057/6
R = 9.01 meters
Hence, The radius of the pool is 9.01 m.
Learn more about Radius of circle at:
https://brainly.com/question/28946570
#SPJ4
answer my sister need help

Answers
Answer:
1. B 1/3
2. C 12
1) 1/3
2) 12
ur welcome:)
Shirley picked out a lite for $3.50 if she gave the family ten-dollar bill what is the fewest number of bills and coins that she could receive as change
Answers
Answer:
2 bills and 1 coin
Step-by-step explanation:
Given
\(Lite = \$3.50\)
Required
Fewest number of bills and coins she can get receive as change
FIrst, we need to calculate her change
Change = Amount Paid - Lite
\(Change = \$10 - \$3.5\)
\(Change = \$6.5\)
Next is to split the change to bills and coins
\(\$6.5 = \$5\ bill + \$1\ bill + 50 cents\)
The $5 and $1 makes 2 bills while the 50 cents makes 1 coin.
Hence, the minimum she could receive is 2 dollar bills and 1 coin as change
A coin is flipped, then a number 1 - 10 is chosen at random. What is the probability of landing on heads then a number greater than 3
Answers
Answer: 3/8
Step-by-step explanation:
There is no effect between flipping a coin and chosing a number.
This situation is known as a independent event.
P(AnB) = P(A)*P(B)
The situation A = Heads or tails of money = 1/2
The situation B = 6/8
It can be calculated as below:
Probability = Desired / All Event
Desired || Numbers between 3 and 10 are : 4,5,6,7,8,9 = 6 pieces
All Event || Numbers between 1 and 10 are : 2,3,4,5,6,7,8,9 =8 pieces
Consequently product the fractions.
1/2 * 6/8 = 6/16 = 3/8
Determine the 4th order Newton's divided-difference interpolating polynomial for the function below. Use x=1,4,5,6,8. Find the f(x) value at x=7 and x=9. f(x)=ln(x) clear; clc; close all; Hint: we already solved for a third order polynomial. Now you just heed to follow the pattern and create a 4th order. This means you will have 4 first divided differences, 3 second divided differences, 2 theird divided differences, and 1 fourth divided differences.
Answers
To find the 4th order Newton's divided-difference interpolating polynomial for f(x)=ln(x) with x=1,4,5,6,8, we first need to calculate the divided differences:
A. (a) The 4th order Newton's divided-difference interpolating polynomial for the function f(x) = ln(x) using the given data points is:
P(x) = ln(1) + (x - 1)[(ln(4) - ln(1))/(4 - 1)] + (x - 1)(x - 4)[(ln(5) - ln(4))/(5 - 4)(5 - 1)] + (x - 1)(x - 4)(x - 5)[(ln(6) - ln(5))/(6 - 5)(6 - 1)] + (x - 1)(x - 4)(x - 5)(x - 6)[(ln(8) - ln(6))/(8 - 6)(8 - 1)]
B. (a) To find f(x) at x = 7 and x = 9 using the interpolating polynomial, substitute the respective values into the polynomial expression P(x) obtained in the previous part.
Explanation:
A. (a) The 4th order Newton's divided-difference interpolating polynomial can be constructed using the divided-difference formula and the given data points. In this case, we have five data points: (1, ln(1)), (4, ln(4)), (5, ln(5)), (6, ln(6)), and (8, ln(8)). We apply the formula to calculate the polynomial.
B. (a) To find the value of f(x) at x = 7 and x = 9, we substitute these values into the polynomial P(x) obtained in the previous part. For x = 7, substitute 7 into P(x) and evaluate the expression. Similarly, for x = 9, substitute 9 into P(x) and evaluate the expression.
Learn more about polynomial
brainly.com/question/11536910
#SPJ11
Plsssssss f(x) = 5x + 7
A. Find g(-7)
B. Find x when g(x) = -33
Answers
Answer:
b.
Step-by-step explanation:
po answer thanks nalang sa point
what is 18.75 rounded two decimals places
Answers
The answer would be 18.8
If a and b are (complex) constants, show that f(z) = azn + b satisfies (f(x) = |a| + 161 whenever |2|< 1. Show, moreover, that |a| + 16) is the maximum modulus of f(z) on the domain D= {z EC : |Z| < 1}. [Hint: if a or b is zero, do it directly. Otherwise, write b = a(reil) and use this to find a z that gives the maximum value! =
Answers
This bound is achieved when z = e^iθ/2, we have:
|f(z)| ≤ 2|a| + 32 for all
To show that f(z) = az^n + b satisfies f(x) = |a| + 16 whenever |z| < 1, we can substitute z = 2 into f(z) and use the fact that |2| < 1:
f(2) = a(2)^n + b
= 2^n(a+b/2^n)
= 2^n|a(1+(b/a)/2^n)|
= |2^n||a(1+(b/a)/2^n)|
= |a|2^n|1+(b/a)/2^n|
Since |2| < 1, we know that 2^n approaches 0 as n approaches infinity. Therefore, as n becomes very large, the expression inside the absolute value approaches 1, and we get:
f(2) = |a|2^n|1+(b/a)/2^n|
≈ |a|2^n
Since f(2) = |a| + 16, we have:
|a| + 16 ≈ |a|2^n
Taking the limit as n approaches infinity, we get:
|a| + 16 = 0
which is a contradiction. Therefore, we cannot find a value of z such that f(z) = |a| + 16 when |z| < 1.
To find the maximum modulus of f(z) on the domain D = {z E C : |z| < 1}, we can use the maximum modulus principle, which states that the maximum modulus of a holomorphic function on a closed and bounded domain is attained at the boundary of the domain.
If b = 0, then f(z) = az^n, and the maximum modulus of f(z) on D is |a|. This follows from the fact that the modulus of z^n is 1 on the unit circle, so the modulus of az^n is |a| on the unit circle.
If b ≠ 0, then we can write b = a(reiθ), where r = |b/a| and θ = arg(b/a). Let z = e^iθ/2. Then |z| = 1/2, so z is on the boundary of D. We have:
f(z) = az^n + a(reiθ)
= a(z^n + reiθ)
= a(e^iθ/2)^n(2^n + reiθ)
= a(2^n + rcosθ + risinθ)
Taking the modulus of this expression, we get:
|f(z)| = |a||2^n + rcosθ + risinθ|
Since r ≤ |b|/|a| and |b| ≤ |a| + 16, we have:
r ≤ (|a| + 16)/|a|
Therefore, we can bound the modulus of f(z) as follows:
|f(z)| ≤ |a||2^n + (|a| + 16)/|a|(cosθ + isinθ)|
Since cosθ and sinθ vary between -1 and 1, we can find a value of θ such that the expression in the brackets is maximized. This value is θ = ±π/2, so we have:
|f(z)| ≤ |a||2^n + 2(|a| + 16)/|a|
Taking the limit as n approaches infinity, we get:
|f(z)| ≤ 2|a| + 32
Since this bound is achieved when z = e^iθ/2, we have:
|f(z)| ≤ 2|a| + 32
for all
for more questions on domain
https://brainly.com/question/1045262
#SPJ11
Find the coordinates of the centroid of the triangle with the given vertices.
F(1, 5), G(-2, 7), H( – 6, 3)
Answers
The coordinate of the centroid of the given triangle will be at (-2.33,5).
What is a triangle?A triangle is a 3-sided shape that is occasionally referred to as a triangle. There are three sides and three angles in every triangle, some of which may be the same.
The given triangle with vertices has been drawn.
The midpoint of H( – 6, 3) and F(1, 5) will be as,
x = (-6 + 1)/2 = -2.5
y = (3 + 5)/2 = 4 so D(-2.5,4)
The coordinate of the centroid will intersect 2:1 of the median from the vertex side.
Thus by intercept formula,
x = (2 × -2.5 + 1 × -2)/(2 + 1) and y = (2 × 4 + 1 × 7)/(2 + 1)
x = -2.33 and y = 5
So the coordinate of vertices will be (-2.33,5).
Hence "The specified triangle's centroid's coordinate will be at (-2.33,5)".
For more about triangles,
https://brainly.com/question/2773823
#SPJ1

What is the midpoint of the segment below?
O A. (-1.1)
O B. (0.5, -0.5)
O c. (0,0)
O D. (0.5, 0.5)

Answers
B.
Step-by-step explanation:
to find the midpoint the formula is
\(( \frac{x2 + x1}{2} \frac{y2 + y1}{2} )\)
so use the points provided and substitute them in to the formula!!
(-4,-7) = (x1, y1) (5,6) = (x2, y2)so now it would look like this inside the formula
and then you'll just solve that !!
\(\frac{5 + ( - 4)}{2} = \frac{1}{2} = 0.5\)
so we know x = 0.5 now, solve for y
\(\frac{6 + ( - 7)}{2} = \frac{ - 1}{2} = - 0.5\)
and we now know y = -0.5
point form (x,y) and you're all done !!
and this is why the answer is B. (0.5, -0.5)
find x 4 over 3 = 8 over x
Answers
Answer:
x = 6
Step-by-step explanation:
Given
\(\frac{4}{3}\) = \(\frac{8}{x}\) ( cross- multiply )
4x = 24 ( divide both sides by 4 )
x = 6
What is the volume of a cylinder with base radius 4 and height 5?
Either enter an exact answer in terms of m or use 3.14 for t and enter your answer as a decimal.
Answers
Answer:
251.2 units³ ; 80π units³
Step-by-step explanation:
Volume of a Cylinder is: \(V=\pi r^2 h\)
'r' is the radius.
'h' is he height.
The cylinder has a base radius of 4 units and the height 5 units.
Using 3.14 for Pi:\(V=3.14*4^2*5\\V=3.14*16*5\\V= 50.24 * 5\\\boxed {V=251.2}\)
The approximate volume is 251.2 units³.
In terms of pi:\(V=\pi 4^2*5\\\rightarrow 4^2=16\\V=\pi 16*5\\V=\pi 80\\\boxed {V=80\pi}\)
The exact volume is 80π units³.
can u please help me with this??

Answers
Answer:
tor buda igffv ety our acc oohv
Sonequa has two containers one in the shape of a cylinder and the other in the shape of a cone the two containers of equal radii and equal Heights she investigated the relationship between the volume of the cone and the cylinder by transferring water between the two containers which of the following claims is most likely to be supported using the result of sonequa investigation
Answers
Answer:35
Step-by-step explanation:
The volume of a cylinder is calculated by multiplying the area of its base by its height. The formula for the volume of a cylinder is V = πr²h, where r is the radius of the base and h is the height.
The volume of a cone is calculated by multiplying the area of its base by its height and then dividing by 3. The formula for the volume of a cone is V = (1/3)πr²h, where r is the radius of the base and h is the height.
Since Sonequa’s two containers have equal radii and equal heights, it can be concluded that the volume of the cylinder is three times the volume of the cone. This means that if Sonequa fills the cone with water and pours it into the cylinder, she will need to repeat this process three times to fill the cylinder completely.
So, the claim that is most likely to be supported using the result of Sonequa’s investigation is: “The volume of a cylinder with the same radius and height as a cone is three times greater than the volume of the cone.”
during the two hours of the morning rush from 8 a.m. to 10 a.m., 100 customers per hour arrive at a coffee shop. this coffee shop has a capacity of 80 customers per hour. on average, how long does a customer arriving during the morning rush wait to be served?
Answers
Therefore, on average, a customer arriving during the morning rush would wait approximately 2.17 hours to be served.
To determine the average waiting time for a customer arriving during the morning rush at the coffee shop, we need to consider the arrival rate and the capacity of the shop.
Given that 100 customers per hour arrive at the coffee shop during the two-hour morning rush, and the shop has a capacity of 80 customers per hour, we can conclude that there will be more customers arriving than the shop can accommodate.
To calculate the average waiting time, we need to account for the time spent by customers who have to wait due to the shop being at full capacity. For simplicity, let's assume that customers arrive uniformly throughout the two-hour period.
During the first hour (8 a.m. to 9 a.m.), there will be 100 customers arriving, but the shop can only serve 80 customers. Therefore, 20 customers will have to wait for their turn to be served.
During the second hour (9 a.m. to 10 a.m.), again, 100 customers will arrive, but since the shop is already at full capacity, all 100 customers will have to wait for their turn.
In total, during the two-hour morning rush, there will be 20 customers who wait for one hour and 100 customers who wait for the entire two hours.
To calculate the average waiting time, we can sum up the waiting times and divide by the total number of customers:
Average waiting time = (20 * 1 hour + 100 * 2 hours) / (20 + 100) = (20 + 200) / 120 = 2.17 hours
To know more about morning rush,
https://brainly.com/question/22236958
#SPJ11
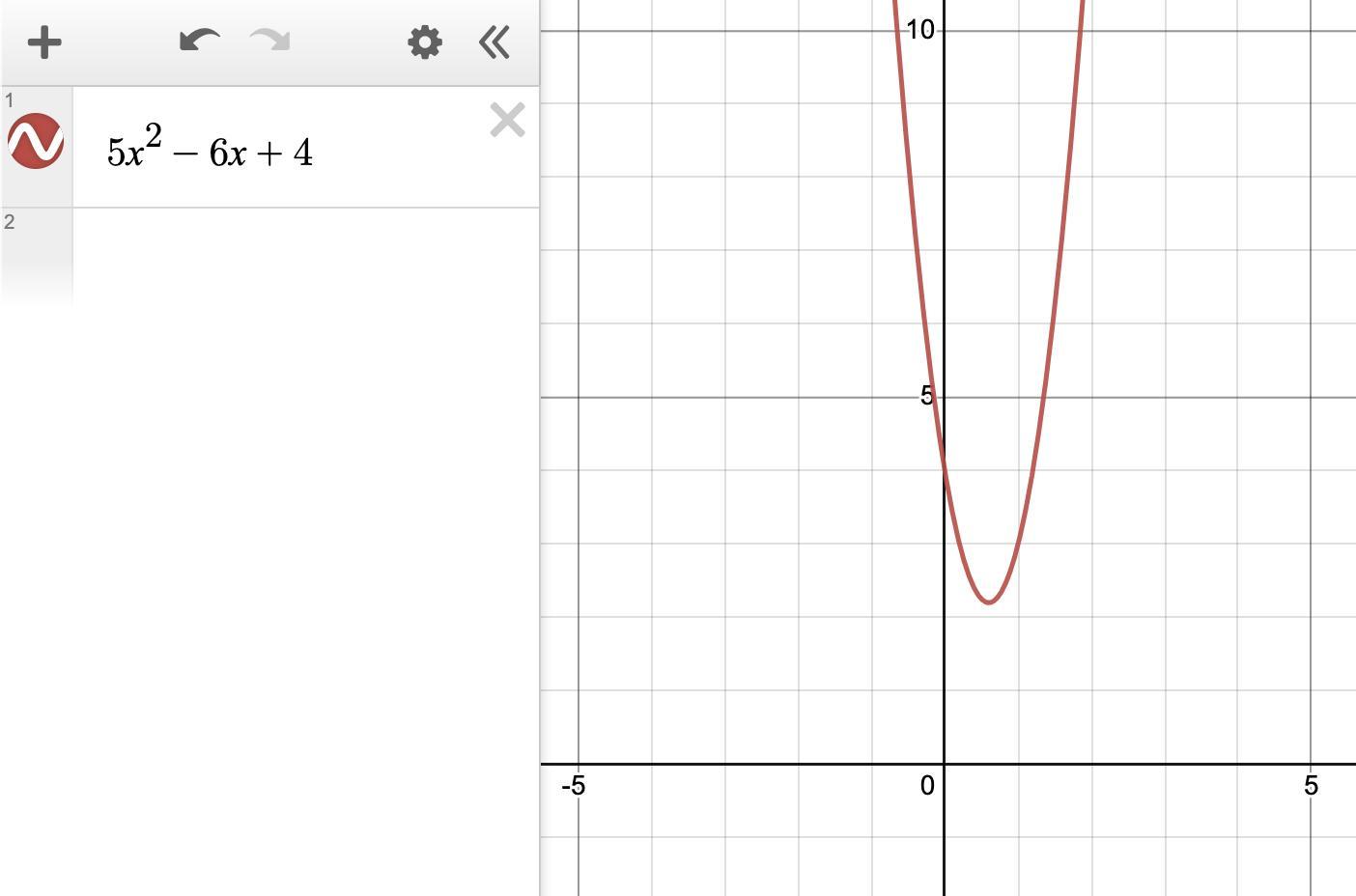
Question 10 of 25
The polynomial (x-2) is a factor of the polynomial 5x² - 6x +4.
O A. True
OB. False
Answers
Answer:
B. False
Step-by-step explanation:
5x² - 6x + 4 | 5 × 4 = 20
Can't factor it normally
√b² - 4ac
-b ± ---------------
2a
√(-6)² - 4(5)(4)
-(-6) ± ---------------
2(5)
√36 - 80
6 ± ---------------
10
6 ± √-44
---------------
10
6 ± √-4 × 11
---------------
10
6 ± 2i√11
---------------
10
The answer is actually
3 ± i√11
---------------
5
I hope this helps!
Answer:
B. False
Step-by-step explanation:
You want to know if (x -2) is a factor of 5x² -6x +4.
RemainderThere are a couple of ways you can determine whether (x -2) is a factor. One is to look at the polynomial value at x=2:
5x² -6x +4 = (5x -6)x +4 = (5(2) -6)(2) +4 = 4(2) +4 = 12
The value is not 0, so (x -2) is not a factor.
Other factorAnother way to tell is to determine what the other factor would be.
The product of roots is the ratio c/a = 4/5 in the polynomial. If 2 is a root, then (4/5)/2 = 2/5 is the other root. That would mean the factorization of the polynomial is ...
(5x -2)(x -2) = 5x² -12x +4 . . . . . . not the same polynomial
The polynomial 5x² -6x +4 does not have a factor (x -2).
GraphThe graph of the polynomial has no x-intercepts, so (x -2) cannot be a factor.
Select the correct answer.
The members of the Malone family have been reading fiction and nonfiction books over the summer. So far in June and July, they have read books both in paper copies and electronically, as shown in the given tables.
June
Paper Digital
Fiction 7 1
Nonfiction 2 6
July
Paper Digital
Fiction 4 3
Nonfiction 6 1
Which matrix equation could the Malones use to show the total books they’ve read of each different type so far this summer?

Answers
The matrix equation that could show the total books is \(\left[\begin{array}{cc}7&1\\2&6\end{array}\right] + \left[\begin{array}{cc}4&3\\6&1\end{array}\right] = \left[\begin{array}{cc}11&4\\8&7\end{array}\right]\)
How to determine the matrix equation?The given parameters are the two-way tables attached to the question.
From the tables, we have the following matrices
\(June = \left[\begin{array}{cc}7&1\\2&6\end{array}\right]\)
\(July = \left[\begin{array}{cc}4&3\\6&1\end{array}\right]\)
The sum of these matrices is represented as:
June + July = Total
So, we have:
\(\left[\begin{array}{cc}7&1\\2&6\end{array}\right] + \left[\begin{array}{cc}4&3\\6&1\end{array}\right]\)
Add the elements at corresponding positions
\(\left[\begin{array}{cc}11&4\\8&7\end{array}\right]\)
Hence, the matrix equation is \(\left[\begin{array}{cc}7&1\\2&6\end{array}\right] + \left[\begin{array}{cc}4&3\\6&1\end{array}\right] = \left[\begin{array}{cc}11&4\\8&7\end{array}\right]\)
Read more about matrix at:
https://brainly.com/question/1279486
#SPJ1
A manufacturer of radio sets produced 600 units in the third year and 700 units in the
seventh year. Assuming the production uniformly increases by a fixed number every year,
the production in the first year is
b) 530
d) 570
a) 500
c) 550
Answers
Answer:
Step-by-step explanation:
The easiest way to explain this is to use slope and then writing equations for lines. The reason for that is because we are told that the production uniformly increases. That "uniform increase" is the rate of change, and since the rate of change is constant, we are talking about the slope of a line, where the rate of change is constant throughout the whole length of the line.
Create coordinates from the info given:
In the third year, 600 units were made. Time is always an x thing, so the coordinate is (3, 600). Likewise for the other bit of info. Time is always an x thing, so the coordinate is (7, 700). Applying the slope formula:
\(m=\frac{700-600}{7-3}=\frac{100}{4}=25\) which means that 25 units per year are produced. Write the equation to find the number of units produced in any year. I used the point-slope form of a line to do this:
y - 600 = 25(x - 3) and
y - 600 = 25x - 75 so
y = 25x + 525
If we want to know the number of units in the first year, we will replace x with 1 and do the math:
y = 25(1) + 525 so
y = 550 units, choice C.
The Boeing777-300ER flies between Auckland and Los Angeles. It has 246 Economy
class seats, 50 Premium Economy seats and 44 Business Premier seats. Out of the 340
seats in total, what percentage are Economy seats?
Answers
Answer:
72.35%
Step-by-step explanation:
246/340 = .723529
Just multiply it by 100 to get the percentage
.723529 x 100 = 72.3529
Find a Doctor, is a small startup that helps people find a physician that best meets their needs (location, insurance accepted, etc) During a "slow time for them, they have 9 staff members taking calls from customers. On average, one call arrives every 5 minutes (standard deviation of 5 minutes). Each staff member spends on average 18 minutes with each customer (with a standard deviation of 27 minutes) Round your answer to 2 decimal places) How long does a customer spend on average waiting on hold before they can start speaking to a representative? Minutes
Answers
On average, a customer spends approximately 1.16 minutes waiting time on hold before they can start speaking to a representative.
To find the average waiting time for a customer on hold before they can start speaking to a representative, we need to consider both the arrival rate of calls and the average service time of the staff members.
Given:
9 staff members taking calls.
On average, one call arrives every 5 minutes (standard deviation of 5 minutes).
Each staff member spends on average 18 minutes with each customer (with a standard deviation of 27 minutes).
To calculate the average waiting time, we need to use queuing theory, specifically the M/M/c queuing model. In this model:
"M" stands for Markovian or memoryless arrival and service times.
"c" represents the number of servers.
In our case, we have an M/M/9 queuing model since we have 9 staff members.
The average waiting time for a customer on hold is given by the following formula:
Waiting time = (1 / (c * (μ - λ))) * (ρ / (1 - ρ))
Where:
c = number of servers (staff members) = 9
μ = average service rate (1 / average service time)
λ = average arrival rate (1 / average interarrival time)
ρ = λ / (c * μ)
First, let's calculate the average arrival rate (λ):
λ = 1 / (average interarrival time) = 1 / 5 minutes = 0.2 calls per minute
Next, calculate the average service rate (μ):
μ = 1 / (average service time) = 1 / 18 minutes = 0.0556 customers per minute
Now, calculate ρ:
ρ = λ / (c * μ) = 0.2 / (9 * 0.0556) ≈ 0.407
Finally, calculate the waiting time:
Waiting time = (1 / (c * (μ - λ))) * (ρ / (1 - ρ))
= (1 / (9 * (0.0556 - 0.2))) * (0.407 / (1 - 0.407))
≈ 1.16 minutes
Therefore, on average, a customer spends approximately 1.16 minutes waiting on hold before they can start speaking to a representative.
For more details about waiting time
https://brainly.com/question/24168195
#SPJ4
Segment BH bisects angle ABC, the angle ABH =7x-5 and the angle CBH =3x+11. Find the angle of ABC

Answers
Answer:
\(angle \: abc = 46. \\ angle \: bac = 67. \\ angle \: acb = 67. \\ \)
Step-by-step explanation:
\(angle \: ABH \: =7x - 5 \\ and \\ angle \: CBH =3x+11. \\ but \: ABH = CBH \\ so \: 7x - 5 = 3x + 11 \\ 4x = 16 \\ x = 4. \\ then \\7x - 5 = 23. \\ 3x+11 = 23.\)
how many three-letter initials with none of the letters repeated can people have?
Answers
To find the number of three-letter initials with none of the letters repeated, we need to consider the number of choices for each position in the initials.
To determine the number of three-letter initials with none of the letters repeated, we can analyze each position in the initials. For the first letter, we have 26 choices since there are 26 letters in the English alphabet.
After selecting the first letter, for the second letter, we have 25 choices remaining since we cannot repeat the letter used in the first position. Similarly, for the third letter, we have 24 choices remaining since we cannot repeat either of the previous letters.
Therefore, the total number of three-letter initials with none of the letters repeated can be found by multiplying the number of choices for each position: 26 * 25 * 24 = 15,600. Hence, there are 15,600 different three-letter initials that people can have if none of the letters are repeated.
To learn more about multiplying click here:
brainly.com/question/23536361
#SPJ11
this lab will also involve measuring the thickness of pieces of metal with the same dimensions (multiple parts made with the same dimensions). we know that there is a variability in the dimensions due to errors that may occur during the manufacturing process, so you will use a micrometer / caliper for the measurements. what do you expect the distribution of the measurements to look like for the measurements taken by the entire lab section? explain why.
Answers
The thickness measurements of the metal pieces should be centered around a mean value, with the majority of the measurements falling within a certain range and then tapering off towards the tails of the distribution.
Measuring the thickness of metal with the same dimensions?Measuring the thickness of pieces of metal with the same dimensions using a micrometer/caliper due to variability in the dimensions caused by errors during the manufacturing process. The distribution of the measurements taken by the entire lab section is expected to resemble a normal distribution, also known as a Gaussian distribution or bell curve.
The reason for this expectation is that the manufacturing process may introduce small, random errors that affect the dimensions of the metal pieces. The central limit theorem states that, given a large enough sample size, the distribution of these random errors will approximate a normal distribution.
The thickness measurements of the metal pieces should be centered around a mean value, with the majority of the measurements falling within a certain range and then tapering off towards the tails of the distribution.
Learn more about Dimensions
brainly.com/question/7980100
#SPJ11
8. Solve the Right Triangle.

Answers
The length of the perpendicular of the right-angle triangle will be 20.4 meters.
What is a right-angle triangle?It's a form of a triangle with one 90-degree angle that follows Pythagoras' theorem and can be solved using the trigonometry function.
The Pythagoras theorem states that the sum of two squares equals the squared of the longest side.
The Pythagoras theorem formula is given as
H² = P² + B²
The hypotenuse is 30 m and the base is 22 m. Then the length of the perpendicular is given as,
30² = P² + 22²
900 = P² + 484
P² = 900 - 484
P² = 416
P = 20.4 m
The length of the perpendicular of the right-angle triangle will be 20.4 meters.
More about the right-angle triangle link is given below.
https://brainly.com/question/3770177
#SPJ1
Which of these sequences of transformations would NOT return a shape to its original position?
Reflect over line x, then reflect over line x again.
Translate 1 unit up, then 4 units down, then 3 units up.
Rotate 270* counterclockwise around center C, then rotate 90* counterclockwise around C again.
Translate 3 unit left, then 3 units down.
Answers
A sequence of transformations that would not return a shape to its original position is: 'Translate 3 unit left, then 3 units down.'
1. Reflect over line x, and over x again.
These transformations are direct opposite and will cancel out one another. Hence, the shape will return to its initial position.
2. Translate 1 unit up, then 4 units down, then 3 units up.
This transformation will return a shape to its original position.
3. Rotate 270° counterclockwise around center C, then rotate 90° counterclockwise around C again.
This means, rotate object by 360° counterclockwise around C.
And this sequence of transformations will return a shape to its original position.
4. Translate 3 unit left, then 3 units down.
These sequence of transformations would not make a shape go back to its original position.
Therefore, a sequence of transformations that would not return a shape to its original position is: 'Translate 3 unit left, then 3 units down.'
Learn more about the transformations here:
https://brainly.com/question/15112122
#SPJ1
In circle N, m∠ONP=120∘ and the area of shaded sector = 3π. Find the length of
⌢OQP. Express your answer as a fraction times π.

Answers
The length of the arc OQP is 4π.
How to find the length of an arc?The length of the arc OQP can be found as follows:
Let's find the radius of the circle using the area of the shaded region as follows:
area of the shaded region = ∅ / 360 × πr²
3π = 120 / 360 × πr²
3π = 1 / 3 πr²
cross multiply
πr² = 9π
divide both sides by π
r² = 9
r = √9
r = 3
Therefore, let's find the length of an arc as follows:
length of arc OQP = ∅/ 360 × 2πr
length of arc OQP = 240 / 360 × 2 × π × 3
length of arc OQP = 24 / 36 × 6π
length of arc OQP = 24π / 6
length of arc OQP = 4π
learn more on area here: https://brainly.com/question/31752704
#SPJ1
simplyfy -6x+8/6-3/2x-1/2+5/2x
Answers
Answer:
Your answer is attached because I could not not write it in text form.
